改進自適應遺傳算法在多載AGV調度的應用研究

劉 暢，張承瑞，孫玉璽

(山東大學 機械工程學院，濟南 250061)

(山東大學 高效清潔機械制造教育部重點實驗室，濟南 250061)

1 引 言

隨著工業4.0時代的智能工廠的引入，工廠規模越來越大，對自動導引運輸車(Automated Guided Vehicle，AGV)的需求量變大，調度復雜性增加，AGV調度機制應該更加高效、魯棒.

現在已經有很多學者對多AGV調度進行研究.Valerio Digani，M.Ani Hsieh等[1]提出一種優化策略，來最大化AGV的吞吐量；Bai Li，Hong Liu，Duo Xiao等人[2]提出一種集中式多AGV運動規劃方法，計算效率更高.但是，國內外研究的多AGV路徑規劃問題大多數是基于單負載，對多負載AGV的研究較少.

Azimi等[3]較早的研究了多載AGV調度需要解決的問題.Ho Y-C，Chien S-H研究多負載AGV的相關問題[4]，并且重點研究了多負載AGV的提取分配原則[5].霍凱歌等[6]，已經對自動化集裝箱碼頭中的多載AGV調度問題進行研究，他們發現，多載AGV比單載AGV效率更高.Li-xiang Zhang等[7]研究了在自動化汽車裝配線環境下，多載AGV高效運輸物料的問題，并使用遺傳算法進行求解.Li-zhen Du等[8]研究了在紡織車間環境下，多載AGV運輸物料的問題，并且使用混合遺傳算法和粒子群算法進行求解.

隨著任務的維數增加，傳統算法求解的時間復雜度大.所以，國內外很多學者使用智能算法(如頭腦風暴算法[9]、粒子群優化算法[10])來對多AGV調度問題進行求解.

上述論文中，大多只是簡單的假設多載AGV運輸1個或2個負載，只考慮負載重量的約束，卻沒有考慮負載的體積約束.

本文第2節描述多載AGV調度問題的環境，第3節對路徑規劃問題進行建模，第4節對初始數據進行預處理之后，使用改進的自適應遺傳算法進行求解，第5節將改進的自適應與標準遺傳算法和自適應遺傳算法進行比較.

2 問題描述

對于工廠的物料運輸問題，在傳統的單載AGV模型中，不需要考慮體積、重量約束，只是將一種物料運輸到目的地，一次只執行一個任務.這極大的浪費了AGV的負載能力.

如圖1所示，AGV沒有任務時，會停靠在充電區域(charge area)，進行充電或者待機.任務集合發布時，AGV從充電區域(charge area)來到倉庫(warehouse).在不超過AGV體積、重量約束的條件下，根據調度算法求解得結果進行加載貨物，然后正式開始運輸貨物.在圖1的多載AGV運輸物料示意圖中，AGV可以根據任務需求自由地到達任意一點.當AGV負載為空時，會返回倉庫(warehouse)進行下一個任務的運載.周而復始，直到所有任務完成后，AGV會回到充電區域進行充電或者待機，直到下一個任務集合的到來.

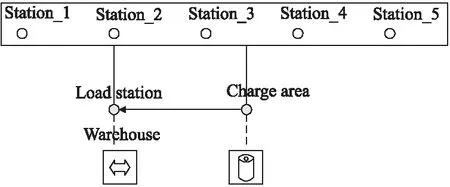
圖1 多載AGV運輸物料示意圖

3 建立模型

本文主要解決的是工廠環境下如何高效調度多載AGV的問題.

3.1 符號說明與模型假設

符號說明

M：表示路徑規劃的路徑數目；

Ni：表示在規劃的第i路徑中，執行任務點的數目；

cij：表示在規劃的第i條路徑中，從倉庫出發到第j個任務點所產生的成本；

Gij：表示在規劃的第i條路徑中，第j個任務點所需要的物料的重量；

G：表示多載AGV可承受的最大重量；

Vij：表示在規劃的第i條路徑中，第j個任務點所需要的物料的體積；

V：表示多載AGV可承受的最大體積；

Aijk：表示第k個任務是否在第i條路徑的第j個任務點被執行；

K：表示任務總數目；

d_list：表示只能被單個運輸的任務點形成的路徑；

dd_list：表示被最短路徑模型求解后得到的路徑集合；

p_list：表示d_list和dd_list兩個集合的并集.

模型假設

1)單個任務的負載不會超過多載AGV的最大載重約束和體積約束；

2)AGV行駛單位長度，成本相同；

3)AGV勻速行駛.

3.2 調度模型

目標函數：

(1)

約束函數：

(2)

(3)

(4)

(5)

公式(1)為模型的目標函數，為距離函數矩陣，表示路徑的成本；公式(2)為多載AGV的重量約束；公式(3)為多載AGV的體積約束；公式(4)、公式(5)，約束任務能且只能被一輛多載AGV完成.

4 改進的自適應遺傳算法

遺傳算法[11]實現簡單，通用性強，易于和其它算法結合，具有并行性和魯棒性.但是，它也存在過早收斂、局部搜索能力弱等問題.

針對標準遺傳算法的上述不足，本文在自適應遺傳算法的基礎上，加入災變操作與逆變操作，提出一種改進的自適應遺傳算法(Improved Adaptive Genetic Algorithm，IAGA)，如圖2所示，其為改進自適應遺傳算法的流程圖.

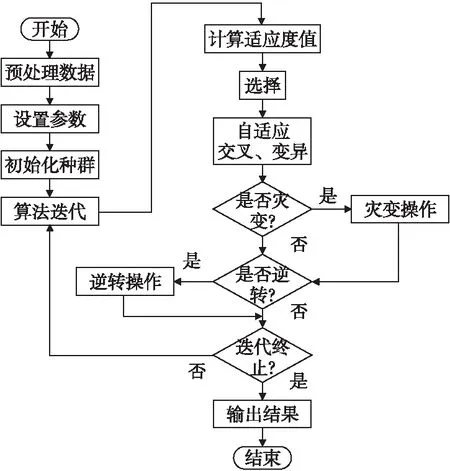
圖2 IAGA流程圖

在初始化種群后，算法進入迭代部分，進行選擇、交叉、變異操作.

然后進入災變操作，根據適應度值，求解災變算子，判斷是否執行災變操作，災變算子隨著陷入局部極值迭代次數的增加，不斷的增加種群的交叉概率和變異概率，使算法更容易跳出局部極值.

之后，進入逆轉操作，即局部搜索部分.當滿足逆轉條件后，進入逆轉操作.在逆轉操作中，添加了倒序操作與插入操作.選取種群的部分染色體，根據倒序概率和插入概率，判斷是否進行倒序操作或者插入操作，執行完畢后，將操作后的染色體的適應度值，與操作前的適應度進行比較.適應度值變大時，才會接受新解.算法將沿著適應度變高的方向進行進化.

最后根據迭代終止條件(迭代次數或者收斂)，判斷是否終止迭代.

4.1 適應度函數

目標函數為最小路徑.為了方便編程和簡化智能算法的迭代過程，本文使用懲罰函數的方式，將重量的約束與體積約束，加入到成本函數中.適應度值為成本的倒數，成本越大，適應度越小.適當調整α，β的值，滿足各個AGV的載重約束和體積約束.

(6)

(7)

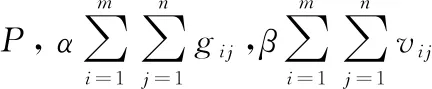
4.2 自適應策略

自適應交叉算子、變異算子

本文采取文獻[11]中，正弦自適應遺傳算法的遺傳算子的求解公式.

(8)

(9)

其中，pc為交叉概率；pm為變異概率；pc1為種群的最大交叉概率；pc2為種群最小交叉概率；pm1為種群的最大變異概率；pm2為種群最小變異概率；fm為種群的最大適應度；fa為種群平均適應度；f′為染色體個體適應度；

自適應遺傳算子隨著適應度的變化而不斷變化，可以很好地提高遺傳算法的收斂速度和性能.

自適應災變算子

傳統的災變算子是固定值，導致對每個算例的適應性不強，需要不斷調整.

本文提出一種自適應災變算子，它隨著陷入局部極值的代數的增加，不斷增加交叉概率與變異概率，使整個種群跳出局部最優解.

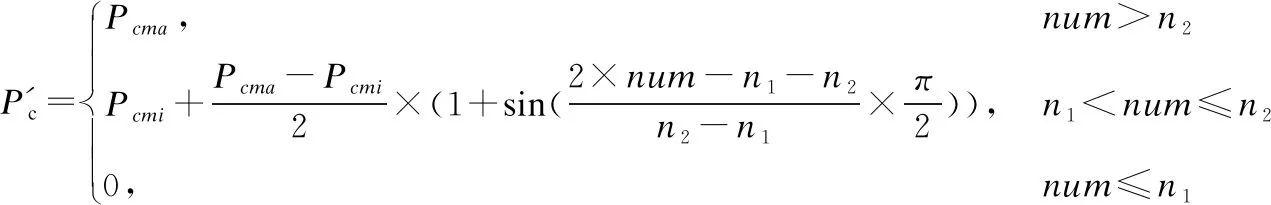
(10)

(11)

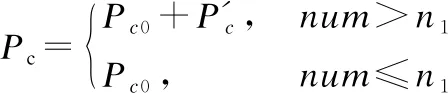
(12)

(13)

災變算子的自適應調整，如圖3所示，在算法迭代初期，種群適應度急劇變化階段，不會發生作用.在種群陷入局部極值后，隨著陷入極值的時間越長，災變算子使得交叉概率和變異概率不斷增大.

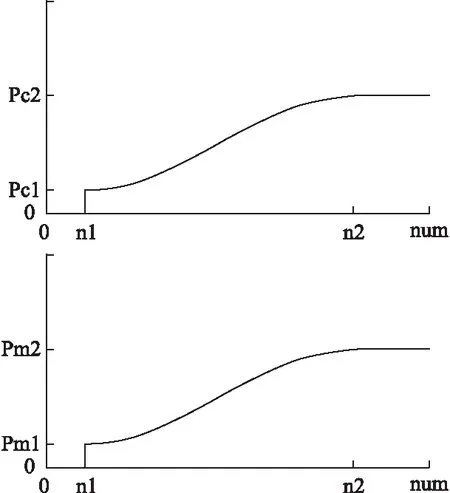
圖3 災變階段交叉概率、變異概率變化量

自適應逆轉算子

本文提出一種自適應逆轉算子，隨著總迭代次數的增加，逆轉算子不斷改變，使得種群進行逆轉操作的概率增大.

(14)

其中，Pi為執行逆轉操作概率；Pim為最大逆轉概率；T為迭代周期；ite為迭代次數.

如圖4所示，在算法的迭代初期，種群的多樣性大，不需要過多的進行逆轉操作.在算法的后期或者迭代陷入局部最優值時，適當的進行逆轉操作，既可以增加種群的多樣性，也有利于跳出局部極值.而且，逆轉操作使得種群向著更加有利的方向進行進化，容易跳出局部極值.

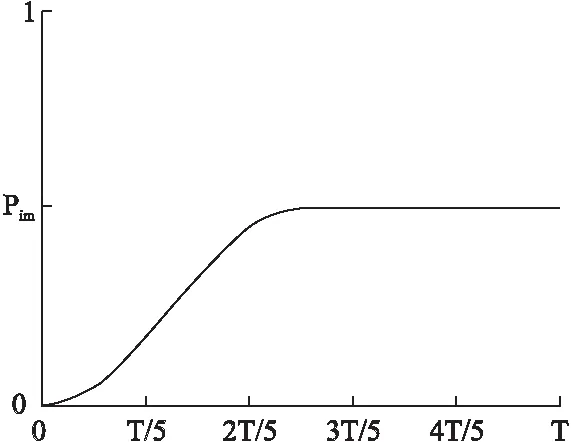
圖4 逆轉操作概率的自適應調整

4.3 算法基本流程

4.3.1 數據預處理

1)剔除重量大或者體積大的任務

分析所有任務點需要的物料的重量與體積，刪除重量很大或者體積很大、無法與其他物料進行一起運輸的物料訂單.這樣的物料只能單載運輸.形成單載AGV路徑集d_list.之后，智能算法求解多載AGV路徑集合dd_list.

剔除重量大或者體積大的任務，將其組合成單獨的任務隊列，可以減少調度系統的搜索的維度，使得算法求解的效率更高，速度更快.

2)根據數據提供的x坐標與y坐標，計算直線距離，提前生成距離矩陣，避免在程序計算中重復計算，降低程序的計算量.

4.3.2 調度模型求解

編碼與解碼

采用實數編碼的策略.常見的二進制編碼雖然簡單易行，不適合高維、高精度優化問題.這里采用實數編碼.

倉庫的編碼：0，分割各個字符串.例如：任務點1-4為一組，6-9為一組，11-14為一組，編碼后的染色體的編碼字符串，1-2-3-4-0-6-7-8-9-0-11-12-13-14，這就是編碼過程.解碼過程則相反.

選擇

本文采用輪盤賭選擇方式.根據每個個體的適應度，按照比例進行概率選擇.適應度越大的染色體被選中的概率越大，反之，適應度越小的染色體被選中的個體越小.

交叉、變異

采用兩點交叉方式.隨機選中小于染色體編碼長度的兩個數，將它與臨近的染色體相同位置進行交換.但是由于采用的是實數編碼.所以，交叉操作完成之后，相應的染色體內部，需要進行調整.

采用單點變異的方式.因本文采用的是實數編碼，所以單點變異后，需要進行調整.

逆轉

選出部分種群，根據設定好的概率(倒序概率，插入概率)，使用逆序排列，插入排列的方式，保留適應度值增大的染色體，否則恢復大原基因排列.這樣做的目的，一是增加種群的多樣性，二是可以向著種群適應度值高的方向進化.

調整

因采用實數編碼，除0外的其他實數應保持數字的唯一性，當進行交叉變異等操作后，需要進行調整，來滿足染色體數字的唯一性.

5 仿真驗證

本文的實驗環境為：Windows 10+MATLAB 2014b.本文的算例由Solomon[12]提出的算例調整修改而來，任務數據包括位置，重量約束，體積約束初始任務數據包括位置，重量約束，體積約束.搭建了一個倉庫點，(N-1)個工作站，在共N個點的環境.多載AGV能承受負載的最大重量為4，多載AGV能承受負載的最大體積為4.

分別在N為30，60，90 3個規模下，各做10組實驗，取得3種規模下，改進的自適應遺傳(IAGA)，標準遺傳算法(Standard Genetic Algorithm，SGA)，自適應遺傳算法(Adaptive Genetic Algorithm，AGA)算法，3種算法收斂的迭代次數、迭代時間、迭代精度.

分析圖5可知，在相同的迭代次數下，改進的自適應遺傳算法比標準遺傳算法、自適應遺傳算法收斂速度更快、更加接近最優值.

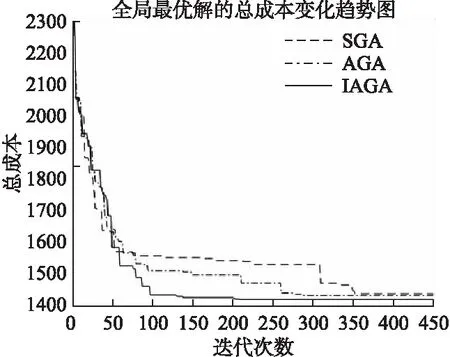
圖5 N=30，各個算法迭代變化趨勢

由表1-表3，比較3種算法在N=30，60，90維度下的的迭代次數、迭代時間、收斂解，可知，改進的自適應遺傳算法迭代次數更少、達到收斂的時間更短，收斂解更加接近最優解.

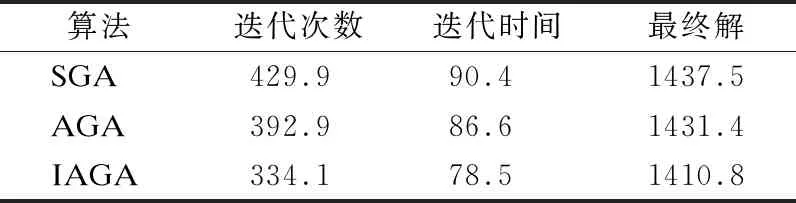
表1 N=30，各個算法比較

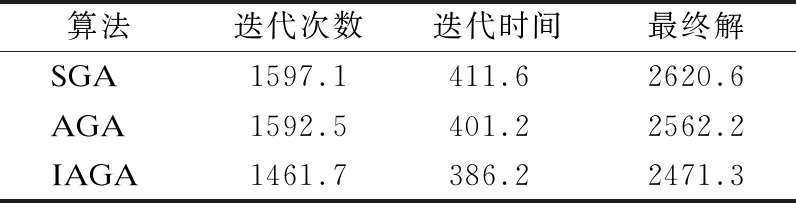
表2 N=60，各個算法比較

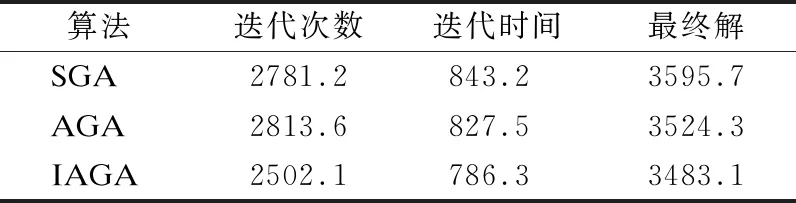
表3 N=90，各個算法比較

6 結 論

本文中，多載AGV調度問題是一個添加了物料體積、重量雙重約束的VRP(Vehicle Routing Problem，車輛路徑規劃問題)問題.本文首先對數據進行預處理，降低求解變量的維度，然后使用改進的自適應遺傳算法(IAGA)進行求解，最后，分別在數據維度N=30，60，90時，進行多組實驗取平均值.與標準遺傳算法(SGA)、自適應遺傳算法(AGA)相比，改進的自適應遺傳算法收斂快，優化效果明顯，收斂精度高.

在求解過程中也發現一些不足：1)在任務合并尋優過程中，迭代時間長，可以進一步改進算法或者調整參數來進行加快收斂；2)本文沒有考慮時間約束，在后續工作中可以加入時間窗約束.