基于Elgamal強盲簽名的區塊鏈電子投票方案研究

邵 清，洪皓潔，李 斌

(上海理工大學 光電信息與計算機工程學院，上海 200093)

1 引 言

投票表決是社會生活中不可缺少的環節，是選舉的一種重要手段.過去人們常用的舉手表決或紙質投票等，都或多或少存在一些問題，如結果容易被篡改、選舉過程不透明等.隨著計算機技術的發展，電子投票開始受到人們的關注，它可以降低選舉的運行成本，同時滿足安全性、隱私性等投票要求.但也存在一些不足之處，如投票者個人信息易泄露、投票過程容易受到攻擊、投票數據易丟失等問題.

一個理想的電子投票系統應該具有的重要特性是：

1)合法性：只有經過授權的選民才能投票；

2)完整性：未經檢測，不應該修改、偽造或刪除選票；

3)可驗證性：可能核實的所有選票都應正確計入結果；

4)隱私性：選民的選票不應在任何階段透露給任何人；

5)匿名性：投票者身份隱藏，任何人不得知曉；

6)公正性：在投票結束前，任何個人或組織不能增加投票者人數或提前披露投票結果；

7)唯一性：每個合法的投票者只能投一次票；

8)穩健性：投票的最終結果不應受到任何因素影響.

電子投票可以應用到社會生活的方方面面，引起了國內外許多研究者的興趣.經研究，目前主要有4類電子投票方案：基于混合網絡的電子投票方案、基于盲簽名的電子投票方案、基于秘密分享的電子投票方案和基于全同態加密的電子投票方案.

基于混合網絡的電子投票方案，可以抵抗被動攻擊，但不能得到混合服務器內部置亂情況.為了解決置亂問題，Furukawa和Sako[1]提出基于混合網絡的電子投票方案，在不泄露操作的情況下證明了置亂過程的正確性.Neff[2]提出了可對數據置亂、混淆的實現方法，效率得到提高，并證明了正確性.Luo等人[3]引入盲簽名等工具，提出了一種新的無收據電子投票方案.方案滿足匿名性要求，但無法滿足普遍驗證性.Zhao和Liu[4]結合Shamir秘密分享和K-匿名提出一種電子投票方案.同年，Yuan和Li[5]基于Mignotte秘密分享，結合中國剩余定理，提出一種可驗證的分布式的電子投票方案，平衡了投票者與計票中心的沖突.但是基于秘密分享的電子投票方案中需要可信任的秘密分發機構和多個計票機構等，這些機構之間的通信復雜度是影響使用的核心要素.Wang等人[6]設計同態密文加法器，結合數字簽名技術，提出一種電子投票方案，實現了匿名性和完整性.He等人[7]利用全同態加密，解決電子投票中的身份認證問題.方案支持多個候選人，并利用全同態加密實現了對選票的加密以及求和.但該方案效率不高，難以在實踐中應用.在2008年中本聰[8]發表比特幣論文后，區塊鏈的關注度大幅提升.區塊鏈的特性很適合應用在投票事件上，與區塊鏈技術結合的電子投票方案解決了許多原有的安全性問題，提高了系統的可追溯性，可以防止惡意攻擊或出現欺詐選票等.Jason等人[9]結合盲簽名技術和區塊鏈，將盲化后的選票寫入交易附加信息，但缺點是仍引入了第三方可信機構.于天嬌等人[10]結合RSA算法，提出了基于聯盟鏈的電子投票方案.可鏈接環簽名實現了投票者匿名性.CRUZ等人[11]提出了基于區塊鏈的投票方案，確保安全和不可篡改，但仍需引入可信第三方.

為了解決現有電子投票方案中存在的隱私泄露、不可公開驗證等安全性問題以及計票效率問題，本文利用區塊鏈技術，結合基于Elgamal的強盲簽名算法和不可鏈接支付技術，提出了一種新的電子投票方案.方案通過強盲簽名算法和哈希函數保證了選票的隱私性、投票者的匿名性，并采用不可鏈接支付技術使得選票接收者的匿名性也得到了保護，計票效率也得到了有效提高.

2 相關知識

2.1 基于Elgamal簽名方程的強盲簽名算法

為實現投票者的匿名性，保護選票隱私，本文采用基于Elgamal的強盲簽名算法[12]對選票進行簽名和加密.在此算法中，簽名者不知道消息內容，且請求簽名者把已簽名的消息公開后，簽名者無法追蹤所簽消息.強盲簽名有很強的抗跟蹤性，應用到電子投票當中可以有效保護隱私.且強盲簽名可以實現對原始消息的鑒別與不可抵賴性，使得投票可驗證.

Elgamal簽名是一種非確定性的雙密鑰簽名體制，可用于數據加密和數字簽名.算法私鑰由特定工具生成，為保證私密性僅由使用者保存.在現有算力條件下，方案采用保證算法安全的最小密鑰長度，為1024bits.公鑰通常由私鑰得出，可以公開.在密碼體制中，理論上密鑰越長，密鑰空間越大，則通過窮舉計算推測出真實密鑰的情況就越難發生，算法安全性也越高.但算法安全性不僅由密鑰長度決定，也與現階段算力和密碼體制本身有關.盲簽名按盲化程度可分為：弱盲簽名、強盲簽名和盲參數簽名方案.本方案中采用強盲簽名算法，用到的簽名方程為r=mk+sx[12].

基于Elgamal的強盲簽名算法可以抵御偽造給定消息的數字簽名的攻擊，也可以抵御竊取簽名者私鑰的攻擊，具有較強的安全性.該算法可以打破投票者身份與簽名之間的聯系，實現投票者匿名性.同時也可以保護所簽署消息的具體內容，從而保護選票隱私.

2.2 不可鏈接支付

采用基于Elgamal的強盲簽名算法只是隱藏了投票者的身份信息，為了進一步提高安全性，還需要隱藏選票接收者的信息.為此，方案引入了不可鏈接支付.

不可鏈接支付技術來自Nicolas Van Saberhagen的白皮書cryptonote2.0[13].通常，經典的比特幣地址一旦公布，就會成為交易的一個明確標識，交易接收者的地址就很容易被“鏈接”.而不可鏈接支付打破了輸入輸出地址之間的關聯，允許用戶發布單一的地址，并接受無條件的不可鏈接支付.其主要優勢是，每個目標地址的密鑰默認都是唯一的.因此就不存在“地址重用”問題，也沒有攻擊者能確定交易是否被發送到特定地址或是同時鏈接到兩個地址.在電子投票中，如果想隱藏交易接收者的地址，我們可以用不可鏈接支付技術來實現.不可鏈接支付的交易模型如圖1所示.每個一次性密鑰，都由接收者的地址和發送方的隨機數計算得到.在交易中，使用一次性密鑰使交易地址不容易被“鏈接”.

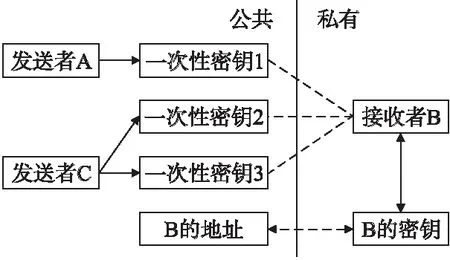
圖1 不可鏈接支付交易模型

3 電子投票方案設計

本文提出的電子投票方案結合基于Elgamal的強盲簽名算法和不可鏈接支付技術，通過獲得節點訪問權后，與區塊鏈上的智能合約進行交互，實現投票過程.

不失一般性，假設一個投票過程需要投票者、接收者和管理者三方共同完成，三方與智能合約進行交互，三方實體交互模型圖如圖2所示.本方案投票過程分為5個階段， 分別是：

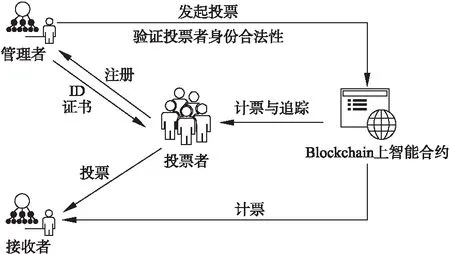
圖2 三方實體交互模型圖

系統初始化階段、注冊階段、選票生成階段、選票接收階段和計票階段.投票方案流程如圖3所示.

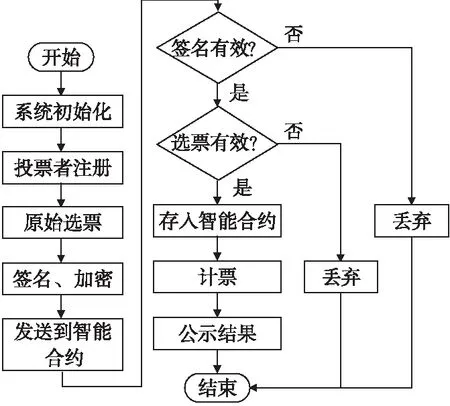
圖3 投票方案流程圖

3.1 符號說明

本節給出文中常用的符號說明，如表1所示.

表1 符號說明

3.2 系統架構說明

本文設計的電子投票方案在以太坊(Ethereum)私有區塊鏈上完成，智能合約控制投票協議，完成整個過程.

投票系統由所有用戶共同維護和管理，并且共享數據信息.投票的詳細信息存儲在每個節點中，不需要集中的數據庫來存儲交易數據，每個節點可以記錄每次選舉的賬本.區塊鏈只允許添加而不允許修改數據，有效地保證了用戶可以進行數據認證.區塊鏈中認定最長鏈為合法鏈，鏈的長度會隨著投票記錄增長.時間戳的存在，使得投票過程是可追溯的.在本方案中，設計了智能合約以實現自動計票，無需第三方參與.智能合約使投票交易自動化，允許雙方直接和自動地達成協議，而不需要中間人，提高了可信度.合約對于所有區塊鏈用戶都是可見的，因此可以很容易地進行驗證.

本方案中，投票由管理者發起，負責每個階段的開始和結束.在投票開始之前，管理者將在鏈上部署智能合約.部署后，智能合約將自動完成整個投票過程.整個電子投票方案架構圖如圖4所示.

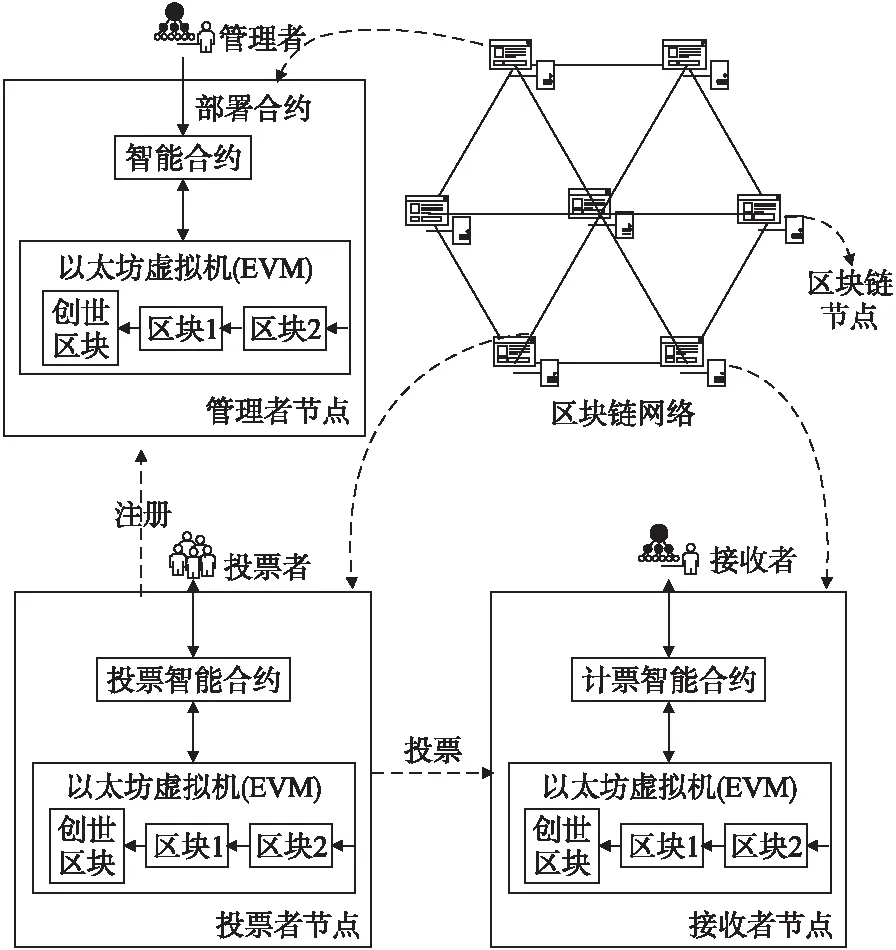
圖4 基于區塊鏈的電子投票方案架構

3.3 系統初始化

電子投票需要管理者來確保整個過程順利進行.管理者由所有投票者選舉得出，在發起投票前，需設置選舉過程中用到的參數并在區塊鏈上公布.所有參與者從公告欄共享信息.理想情況下，我們希望整個投票過程都是通過智能合約來驅動的，確保投票、審核、計票的每一步都是在全體選民的監督下進行.

1)管理者設置項目名稱、投票問題及選項等；

2)設置開始和結束時間點，包括注冊開始時間、注冊結束時間、投票開始時間和投票結束時間；

3)參數設置完成并發布后，投票者將被告知可以開始注冊，同時告知智能合約進入下一階段.

3.4 注冊階段

注冊登記由投票者提出申請，根據基于Elgamal的強盲簽名算法生成私鑰并計算公鑰.投票者只有提交公鑰和個人信息后，才能成為合法投票者，合法投票者名單將被寫入投票者列表.注冊階段應在規定的時間節點前完成，超時系統將不接受任何注冊請求.整個注冊流程如下：

1)投票參與者提出注冊申請；

在初中語文教學中，課本提供的至多只是一幅彩色的畫面，產生的視覺效果差，難以激發學生的興趣。運用現代多媒體技術的聲音、形象動感手段，創造與渲染氣氛，調動學生的感覺器官和思維器官，使他們耳濡目染、身臨其境，進入課文所描述的情境，和作者的思想感情共鳴。這樣能給學生更直觀的感受，不僅加深了學生對課文內容的理解，而且為課堂教學推波助瀾，激發了學生的學習興趣。

2)投票者生成隨機數z∈Zp作為私鑰，計算y=gzmodp為公鑰；

3)投票者將個人公鑰y及身份信息發送給管理者進行注冊；

4)管理者審查投票者是否有投票資格，審查通過后向投票者發放身份ID和證書，并將ID發送給智能合約；

5)注冊完成后，管理者公布合法投票者總數及投票者名單.

隨后，管理者通知智能合約進入選票生成階段.

3.5 選票生成階段

在此階段，投票者需要生成選票，并利用基于Elgamal方程的強盲簽名算法，對選票進行加密和簽名.一張有效選票需包含正確格式的投票字符串和接收者驗證后的簽名.

選票生成過程如下：

1)投票者從智能合約中獲得投票問題與候選項等信息，生成原始選票m；

2)投票者V結合基于Elgamal的強盲簽名算法用私鑰對選票進行簽名，過程如下：

Step 1.V生成隨機數k∈ZP-1，計算r=gk，發送給S；S生成隨機數β∈Zp-1，盲化消息m得到m′，即：

m′=βr-β+1mmod(p-1)

(1)

然后把m′發送到V；

Step 2.V對盲化的消息m′簽名，計算：

r=m′k+sxmod(p-1)

(2)

得到s，把簽名(m′，(r，s))發送給S，簽名記為skV(hash(m))；

3)V對消息m計算哈希得到hash(m)，用接收者的公鑰對哈希值進行加密，記為pkS(hash(m))，這是構成選票的主要信息；

4)V創建包含加密后的哈希值pkS(hash(m))和簽名skV(hash(m))的選票，并通過區塊鏈將選票發送給S.

3.6 選票接收階段

在選票接收階段，本文采用不可鏈接支付技術來隱藏選票接收者S的身份信息，標準投票交易結構如圖5所示.通過計算生成一次性不可鏈接地址，由于使用了哈希函數，根據已公開的P和R，第三方無法逆推得到接收者公鑰對(A，B)，所以也無法知道S的身份信息.這就隱藏了交易接收者的地址.

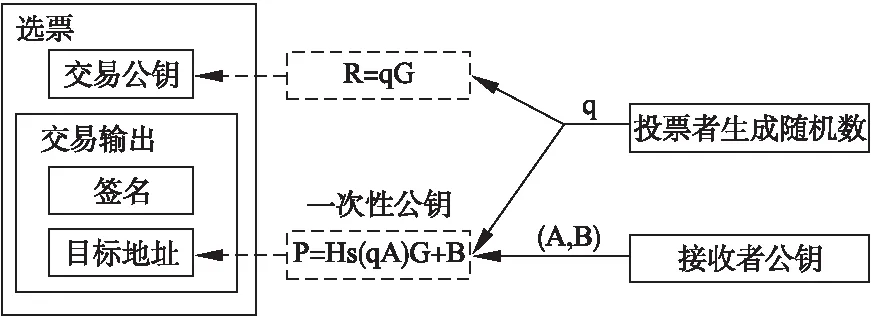
圖5 標準投票交易結構

選票接收步驟如下：

Step 1.S選取兩個數a，b作為私鑰，計算出對應的公鑰A=aG和B=bG，并對全網公布這兩個公鑰；

Step 2.V隨機選取正整數q作為私鑰，計算一次性公鑰P，R：

P=HS(qA)G+B

(3)

R=qG

(4)

Step 3.(P，R)經哈希函數運算后，得到一次性不可鏈接地址，V將不可鏈接的一次性地址和投票記錄公布到區塊鏈上.S用私鑰(a，b)掃描區塊鏈，檢查每個經過的投票交易.

若S是交易的接收者，那么aR=aqG=qA，則：

x=Hs(aR)+b

(5)

xG=(Hs(aR)+b)G=Hs(aR)G+bG=Hs(aR)G+B=P

(6)

驗證發現符合橢圓曲線加密算法的定義，x即為針對一次性公鑰P的私鑰，其他人是不可知曉的.此時，S接收到加密選票，且不會暴露自己身份.

S進行逆盲變換，計算：

r′=rβmod(p-1)

(7)

s′=r′r-1smod(p-1)

(8)

得到簽名(m，(r′，s′))，但不會知曉消息內容.同時，S用公鑰pkV去驗證簽名的有效性.若簽名無效，則忽略；有效則發送回V.

S用私鑰sks解密，得到hash(m).哈希函數的存在，使得原始選票內容不可逆推，即S不知道消息m，也就無法知道V的選票投給了誰，從而保證了選票的隱私性.一旦選票被記錄在區塊鏈上，V的投票任務就完成了.

之后，S將選票發送給管理者，進入計票階段.

3.7 計票階段

到達規定的投票結束時間時，管理者向智能合約發送通知，智能合約將檢查所有投票者是否都完成投票.接著，智能合約停止接收投票者的選票，并對接收到的全部選票進行統計，還未投票的投票者視為棄權.計票時，智能合約對于接收到的每一張選票，檢查是否包含用于簽名該選票的隨機數k，如果不存在則接收該選票，存在則拒絕接收.在所有驗證之后，包含選票的區塊將被添加到區塊鏈中，其他的對等節點則驗證并更新他們的鏈.結果會在鏈上以廣播形式發布，區塊鏈中的所有節點都會同步消息以確保數據準確性.

具體計票過程如下：

1)首先，投票者審查自己的選票是否被記錄，若沒有，則可以提出申訴，要求智能合約添加自己的選票；

2)智能合約檢查投票記錄是否已經存在；

3)智能合約將收到的選票密文與投票者列表ID進行對比，將未收到的選票視為棄權票；

4)統計選票，增加相應候選者的票數；

5)智能合約宣布投票結果，并共享給所有節點.

4 本文方案分析

4.1 安全性分析

為了評估所提電子投票方案的安全性，采用STRIDE威脅建模方法，分析系統受到的威脅.威脅建模讓我們從攻擊者角度去思考問題，更好地去分析每個組件是否可能被篡改、仿冒或是信息泄露等.威脅建模數據流圖如圖6所示.

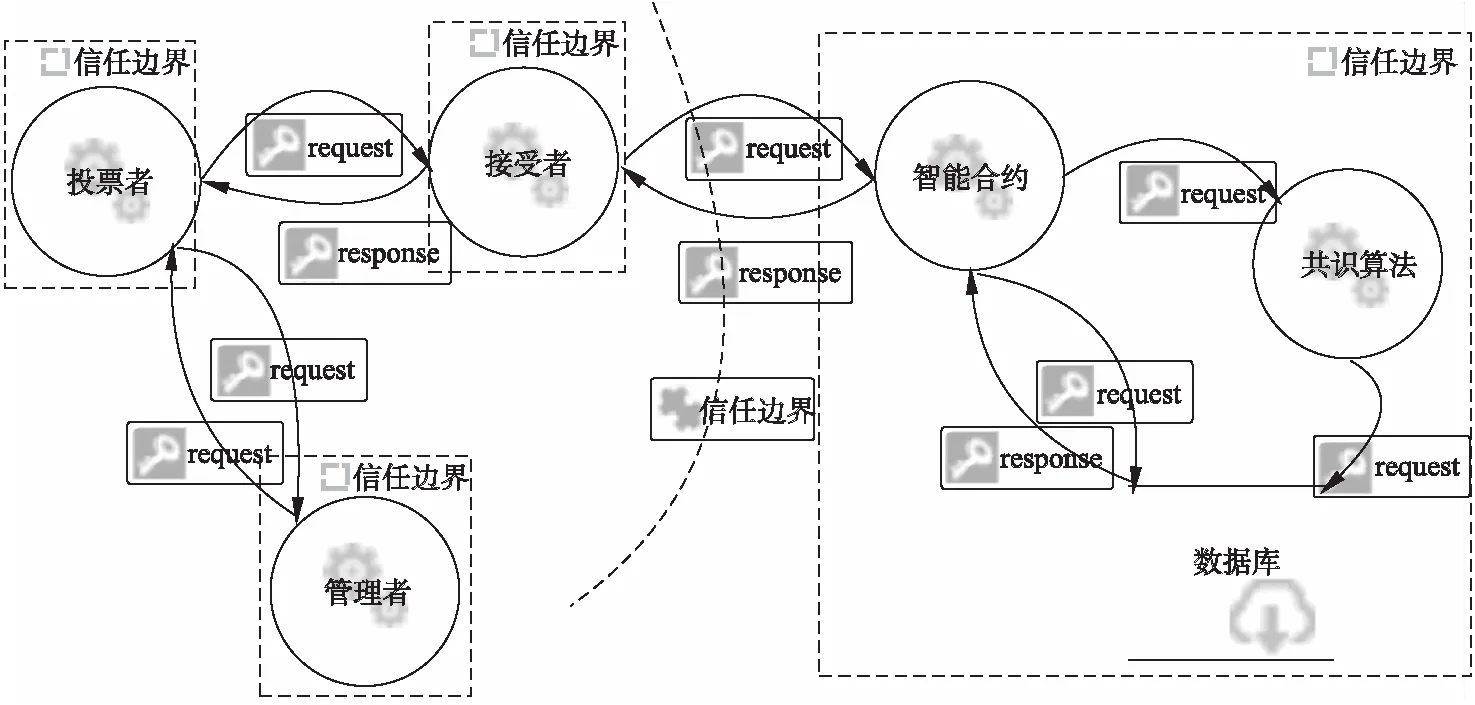
圖6 投票方案數據流圖

分析建模報告可知本文方案面臨的威脅主要有欺騙攻擊、拒絕服務等.投票者和管理者可能會被攻擊者欺騙，在惡意節點上進行投票.這種情況需要惡意節點擁有超過全網51%的算力，可能性非常小.拒絕服務是指消耗資源或者服務、功能不可用.分布式的賬本數據庫，保證了即使某一節點受到攻擊，整個系統數據仍能更新，不會丟失，但這帶來的資源消耗問題也是值得重視的.服務不可用情況一般是負載均衡沒有做好，本方案屬于小規模投票，不存在訪問壓力過大情況，一般不會出現.區塊鏈的去中心化有效保障了節點安全，但我們需要足夠多的節點來保護網絡，否則也會增加51%的攻擊風險.本方案的設計是為了實現加密傳輸選票并能自動正確計票，從這一角度來看，安全性還是可以得到保證的.

下面對方案的其他屬性進行簡要分析：

1)合法性：結合了基于Elgamal的強盲簽名算法的投票方案，利用盲簽名的不可偽造性，任何非法人員都無法獲得身份授權，有效維護了投票者身份的合法性.

2)完整性：由于區塊鏈不可篡改的特性，在所有選票被發送到智能合約后，任何人都不能對其進行修改和刪除，并且這一過程是所有節點共同監督的.由基于Elgamal的強盲簽名算法可知，投票者的私鑰不泄露情況下，他人無法進行冒充投票.

3)可驗證性：本方案提供了公開驗證投票過程的機會，根據智能合約公布的總票數份額，以及給投票者發送的簽名認證，對等節點或任何人都可以監視正在發生的投票活動，每位投票者都可以查看自己的選票是否被統計.

4)隱私性：強盲簽名和哈希函數的存在使得任何人都不知道原始消息m，保護了選票隱私，即保護了候選者隱私.采用一次性不可鏈接地址，使任何人不可逆推公鑰對(A，B)，保護了選票接收者的隱私.

5)匿名性：投票者在投票過程中，利用接收者公鑰對選票進行加密，利用自身私鑰對選票簽名，除了投票者本人，任何人都不能將投票者的身份信息和簽名、加密選票間建立聯系，即實現了投票者匿名.

6)公正性：在到達規定的投票結束時間時，智能合約開始自動執行計票，無需第三方機構參與，并只對有效選票進行統計，投票結果無法被任何人或機構知道，滿足了公正性.

7)唯一性：注冊階段，每個投票者會生成一個唯一的隨機數作為標識，在后續投票中，如果重復計算了隨機數，就認為該投票者重復投票，是無效的.基于Elgamal的強盲簽名算法確保了一個投票者只能簽名一次，只能進行一次投票，滿足了唯一性要求.

8)穩健性：整個計票過程由智能合約完成，投票時間截止后，將不再接收選票.選舉結果在公布在公告欄，任何人都無法修改投票最終結果.區塊鏈共識機制使得所有對等節點同步消息，且投票不可篡改，投票過程滿足穩健性要求.

4.2 對比分析

本節將該方案與文獻[14]和文獻[15]提出的方案進行定性對比分析，結果如表2所示.

表2 不同電子投票方案對比分析

文獻[14]利用分布式Elgamal算法對已有的安全電子投票方案進行了改進，有效隱藏了傳輸矩陣中的數據，使得串謀者無法得到傳數矩陣中的具體數值，有效保護了選票隱私，實現完全保密性.方案的不足是仍要求第三方計票機構絕對.文獻[15]提出了基于區塊鏈的電子投票方案，方案中利用了分布式Elgamal加密體制和零知識證明協議，保證了選票內容的安全傳輸，保證了投票者及選票內容的合法性，有效防止重復投票.但方案可能會泄漏候選者的隱私，也沒有考慮到大規模投票場景.和上述兩種電子投票方案對比，本文方案取消了傳統方案中的計票第三方，滿足了區塊鏈去中心化的特性，避免了計票機構的欺騙行為，保護了投票者和候選者的隱私.

5 性能分析

本方案的性能分析實驗在本地以太坊私有區塊鏈網絡上進行，系統為ubuntu 18.04.

為了驗證方案的正確性與有效性，通過調試不同數量的投票者，在不同數量的候選者情況下，對計票時間進行統計，結果如圖7所示.可以看出，計票時間與投票者數量基本呈線性相關，即隨著投票者數量的增多，計票時間也相應地增加，候選者數量的不同對計票耗時無較大影響，因此本文方案能夠滿足基本投票場景要求.

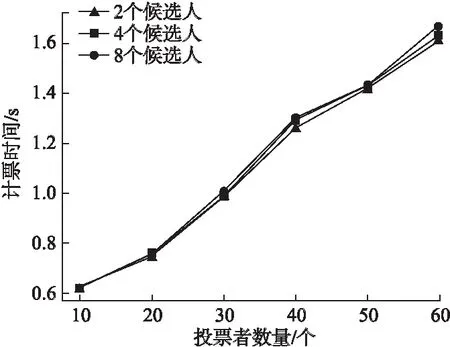
圖7 不同投票者數量下計票時間對比

為了驗證計票效率，將本文方案與文獻[14]和文獻[15]方案在相同數量候選者、不同數量投票者情況下所用計票時間進行對比，結果如圖8所示.圖8表明隨著投票者數量增多，方案所用時間都相應地增多，但時間差卻逐漸增大.本文方案計票耗時相較于文獻[14]和文獻[15]來說，整體較少，計票效率有一定提高.

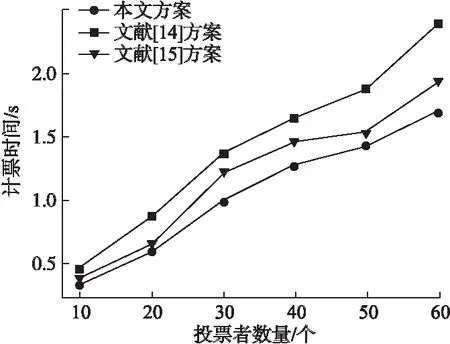
圖8 不同電子投票方案計票時間對比

為了驗證方案的匿名性，以條件熵[16]作為評價指標，來表示不確定度.由于候選者的支持者肯定會將票投給該候選者，這里指的是保持中立的投票者的匿名性.將投票者匿名性定義為投票者選擇的不確定性，這樣就可以用條件熵來量化匿名性.

簡化投票模型，假定只有兩個候選者P1、P2，得票數分別為p1、p2，保持中立的投票者數量為d，則三者之和即為投票者總數.下面給出當投票者組成為P1：P2：d=1：1：2時，條件熵與投票者數量的關系.H(X|Y)表示投票結果只公布勝出者，不公布各候選者具體得票數情況下的條件熵；H(X|Z)表示宣布各候選者具體得票數情況下的條件熵.實驗結果如圖9所示.

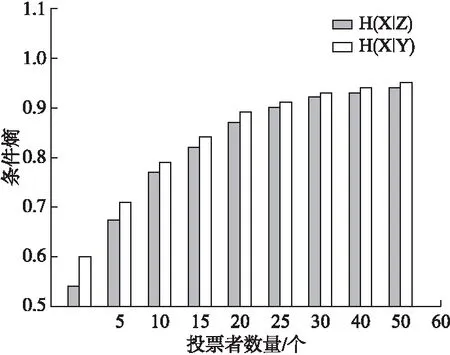
圖9 投票者匿名性與投票者數量的關系

計票結果未公布時，投票者完全匿名，即條件熵為1.由圖9可以看出，公布計票結果，使得投票者的匿名性降低.隨著投票者數量的增加，即投票規模越大，投票者匿名性越高.H(X|Y)與H(X|Z)始終存在差值，即在公布所有候選者得票數情況下，投票者身份更易泄漏，匿名性更低，這也是符合常理的.在電子投票中，為了保證投票者匿名性，有時可以選擇不公布各候選者的得票數，公布結果的方式可以根據實際情況適當調整.

6 結束語

本文通過分析區塊鏈的底層密碼學原理，結合基于Elgamal的強盲簽名算法和不可鏈接支付技術，提出了一種可公開驗證的匿名電子投票方案.智能合約的存在，允許在沒有可信第三方的基礎上完成選票的統計，提高了計票效率，并能對欺騙行為進行檢測.區塊鏈技術確保各節點共同維護賬本信息，降低了傳統中心機構對數據的絕對控制權，同時可以避免因中心機構故障導致的數據丟失問題.方案滿足電子投票的基本安全性需求，實現了較好的匿名性，在計票效率上有一定程度的提高，符合實際投票場景需求.