Supersymmetric structures of Dirac oscillators in commutative and noncommutative spaces*

Jing-Ying Wei(魏靜瑩) Qing Wang(王青) and Jian Jing(荊堅)

1Department of Physics and Electronic,Beijing University of Chemical Technology,Beijing 100029,China

2College of Physics and Technology,Xinjiang University,Urumqi 830046,China

Keywords: Dirac oscillator,anti-Jaynes-Cummings model,Jaynes-Cummings model,supersymmetry

1. Introduction

Dirac oscillator was introduced in Ref.[1]and further illustrated in Ref. [2]. The interaction term was introduced by the replacementpi →pi ?imβωxifrom the free Dirac Hamiltonian. It could be regarded as a relativistic generalization of the non-relativistic harmonic oscillator since it reduced to the non-relativistic harmonic oscillator together with a strong spin-orbit interaction in the non-relativistic limit.[3]Due to its exact integrabilities and wide applications, Dirac oscillator was studied extensively from various aspects[4-9]since it has been introduced. Interestingly,it has been realized experimentally in recent years.[10,11]

The relations between the planar Dirac oscillator and the quantum optics model were revealed in Ref. [12]. In this paper, authors found an exact map from 2+1-dimensional Dirac oscillator to the Jaynes-Cummings (JC) model, which described the interaction between a single-mode quantized electromagnetic field and a two-level atom in the rotatingwave approximation.[13]Then, this work was generalized to the model of a charged planar Dirac oscillator coupling to a uniform magnetic field. In Ref. [14] authors showed that this model could be mapped onto a quantum optics model,which contained both the anti-Jaynes-Cummings (AJC) and the Jaynes-Cummings interactions. Interestingly, each interaction only depended on certain chiral phonons, and there was a competition between these two opposite chiral phonons when the magnetic-field intensity changed. Moreover, when the magnetic field intensity passed the critical point,a chirality quantum phase transition[15]would occur. Shortly after,an alternative approach to study this model was suggested.[16]

The symmetry properties of Dirac oscillator were also investigated. In Ref. [17], authors found that the symmetric properties of a 3+1-dimensional Dirac oscillator were described by so(4)⊕so(1,3). Interestingly,authors of Ref.[18]found a supersymmetric structure in 3+1-dimensional Dirac oscillator. In the work[19], authors found an so(4)algebraic structure in 1+1-dimensional Dirac oscillator.

One the other hand, the noncommutativity becomes one of the foci of the theoretical research nowadays. The concept of the spatial noncommutativity was introduced in physics in the middle of 1940s.[20]At the end of 1990s,it was found that spatial noncommutativity could be derived naturally from the superstring theories.[21-28]Since then,both quantum field theories and quantum mechanics in the noncommutative space have been extensively studied.[29-44]The noncommutative phase space,i.e.,both coordinates and momenta are noncommutative,also attracted much interests.[45-49]

In this paper,we will study the supersymmetric structures of the model of a charged Dirac oscillator interacting with a uniform perpendicular magnetic field both on commutative and noncommutative planes. The organization of this paper is as follows. In Section 2,we will study this model on the commutative plane. We will show that this model has anN=2 supersymmetric structure. We construct the generators of the supersymmetric structure explicitly and then map them onto the ones which only contain left or right-handed phonons according to the signs of a dimensionless parameter. Then, in Section 3, we generalize our studies to the noncommutative case. The corrections due to the noncommutativity are studied. Some conclusions and remarks will be given in the last section.

2. The charged Dirac oscillator in the commutative plane

The model we will analyze is a charged planar Dirac oscillator in the background of a uniform perpendicular magnetic field. The Hamiltonian of this model is

In view of the interaction strengthsglandgr, one finds that the dimensionless parameterζseparates the model (1)into two distinct regions. They are theζ>0 andζ<0 regions, respectively. In the regionζ>0, the AJC interaction is stronger than JC interaction,i.e.,|gl|>|gr|,so the AJC interaction is dominated. Contrarily,in the regionζ<0,the JC interaction dominates.

It was shown that by applying unitary transformations,one can map the Hamiltonian(8)to the ones which only contain AJC or JC interaction according to the signs of the dimensionless parameterζ.Furthermore,a quantum phase transition would happen whenζpassed the zero point.[14,16]This quantum phase transition was named chirality quantum phase transition since the chiralities of the phonons would also change abruptly at the critical point.[14]

Obviously, Hamiltonian (13) shares the common eigenfunctions with Hamiltonian (1). Therefore, it plays the same role as Hamiltonian(1). In Ref.[18], authors found a hidden supersymmetric structure in the 3+1-dimensional Dirac oscillator and constructed the generators which contained a similar Hamiltonian(13). The supersymmetric structure in model(1)is described by Hamiltonian (13) and two supercharges. The two non-Hermitian supercharges are

Thus,it shows that the model(1)possess anN=2 supersymmetric structure.

The generators of the supersymmetric structure, i.e, the Hamiltonian(13)and the supercharges(16), contain both the left and right-handed phonons. Inspired by the work,[14,16]we show that the generators of the supersymmetric algebra can be expressed by the phonons with certain chiralities. This purpose can be realized by a unitary transformation. The unitary operator is

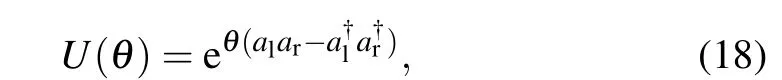
whereθis a parameter which will be determined according to the regions the parameterζcharacterized. The unitary operatorU(θ)transforms the chiral operatorsal, aras

Therefore,in the regionζ<0,the generators of the supersymmetric structure only contain the right-handed phonons.

3. The charged Dirac oscillator in the noncommutative plane

In this section, we will generalize the studies in the previous section to the noncommutative plane. The noncommutative plane we considered is characterized by the algebra(in order to avoid the problem of unitary, we only consider the noncommutativities among position-position and momentummomentum)[45-48]

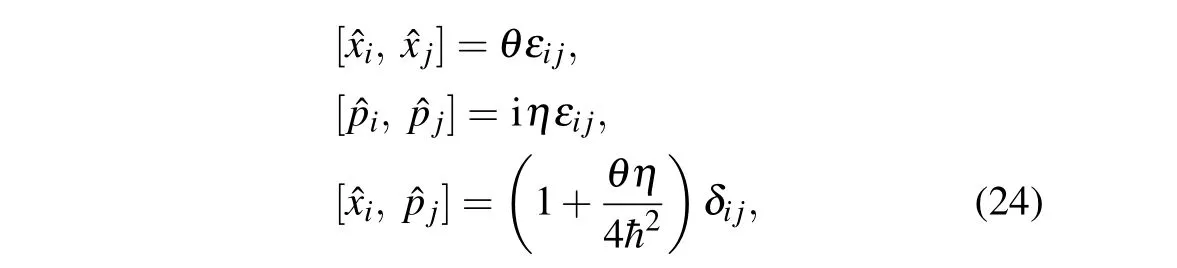
whereθ,ηare two parameters which are characteristics of the noncommutativities.

The Hamiltonian in the noncommutative space(24)takes the same form as the commutative one(1). However,the variablesxi,piin Hamiltonian (1) are replaced by the noncommutative ones ?xi, ?pi. We map the noncommutative variables(?xi,?pi)to the commutative ones by the Bopp shift

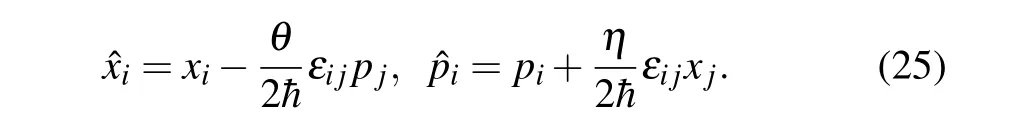
In Ref. [47], authors proved that in order to keep the gauge invariance of the charged Dirac particle interacting with the magnetic field in noncommutative space,we must drop the noncommutativity between the spatial coordinates. Therefore,we setθ=0 in the following.

Mapping the noncommutative variables ?xi,?pito the commutative ones via the Bopp shift and defining a new parameter with the frequency dimension

we get the Hamiltonian

The results(36),(38)not only indicate that the noncommutative generalization of the model (1) possesses anN=2 supersymmetric structure,but also imply that similar with the commutative case,the generators of the supersymmetric structures can also be constructed by using phonons with certain chiralities.

4. Conclusion

In this paper,we study the supersymmetric structures of a charge planar Dirac oscillator in the background of a uniform perpendicular magnetic field. We find that this model possesses anN=2 supersymmetric structure in the commutative space.

Previous studies showed that the model(1)would experience a chirality quantum phase transition when the parameterζpasses the critical point. Our studies show that the chiralities of the phonons which construct the generators of the supersymmetric structures change abruptly when the quantum phase transition occurs. It can certainly be regarded as an evidence of the chirality quantum phase transition.

Then we generalize our studies to the noncommutative space(24). Noticing the fact that the spatial noncommutativity should be dropped for the charged Dirac particle interacting with the magnetic field, we confine ourselves toθ=0. Our results show that the model (1) also has anN=2 supersymmetric structures in the noncommutative plane(24).