A composite micromotor driven by self-thermophoresis and Brownian rectification*

Xin Lou(婁辛) Nan Yu(余楠) Ke Chen(陳科) Xin Zhou(周昕)Rudolf Podgornik and Mingcheng Yang(楊明成)

1University of Chinese Academy of Sciences,Beijing 100049,China

2Beijing National Laboratory for Condensed Matter Physics and Key Laboratory of Soft Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

3Institute for Advanced Study,Shenzhen University,Shenzhen 518060,China

4Songshan Lake Materials Laboratory,Dongguan 523808,China

5Wenzhou Institute,University of Chinese Academy of Sciences,Wenzhou 325001,China

Keywords: Brownian motors,self-phoretic microswimmers,thermal noise,hydrodynamic effect

1. Introduction

Active matter consists of units that individually convert environmental or stored energy into self-propulsion or mechanical force[1]- as is the case for motor proteins,bacteria and artificial active colloidal particles - becoming a fascinating subject of nonequilibrium physics and micro-/nanotechnology. Due to intrinsically out-of-equilibrium features, active matter often exhibits exotic phenomena that are unattainable in equilibrium systems, including the motilityinduced phase transition,abnormal rheology as well as emergent collective behavior.[2-7]Generally, microscale active units are also called micromotors in order to highlight their similarities with macroscopic motors. In terms of the inevitable thermal and/or other types of noise, micromotors can be roughly classified into Brownian motor type and selfpropelled active particle type,for whose performances the effect of the noise is positive and negative,respectively.

Brownian motors refer to submicron-scale machines,which can utilize - but do not necessarily have to - noise combined with unbiased external input signals to achieve a directed motion in asymmetric rachet potentials,[8-13]such as biological ion pumps and bio-molecular motors.[14-19]When the external ratchet potential is time-modulated to alternately switch on and off, such microdevices are termed pulsatedratchet-type Brownian motors.[12]The interplay between the time-modulated ratchet potential and noise generates a directed drift without any net external force. On the other hand, self-propelled active particles generate a driving force along their inherent axis through different physical and chemical effects such as non-reciprocal shape change, bubble release or self-phoresis. Prominent examples would include biological microorganisms[20,21]and artificial active Janus colloids.[22-28]In these cases the external ratchet potential is absent and the noise only disturbs the persistent directed swimming motion of the active particle, randomizing its trajectory. Consequently,the self-propelled particles behave like effective Brownian particles at long timescales. The thermal noise is in this case thus not conducive to the operation of the self-propelled active particles,demanding an extra steering strategy to achieve a directed transport on large length scales.

Given the negative effect of thermal fluctuations on the self-propelled particle, an interesting issue emerges, whether the self-propelled particle can actively exploit thermal noise to improve its performance? Inspired by the Brownian motor,a possible and straightforward scheme would be to construct a composite micromotor by combining the self-propelled particle with the Brownian ratchet. Such a composite motor could possess features of both, the self-propelled particle as well as the Brownian motor. Recently, static asymmetric external fields or boundary walls have been employed to regulate the motion of the self-propelled particles,[29-31]although these designs still correspond to a Brownian motor,in which the active motion acts like an input signal. More recently, rectification of active Brownian particles by a time-oscillating potential has been numerically investigated,[32]with the self-propulsion artificially imposed rather than arising naturally from a physical process. In addition, the hydrodynamic effects have not been taken into account in this case.

In the present work,based upon the mesoscale fluid simulations, we investigate the transport of a two-dimensional self-thermophoretic Janus particle in a time-modulated dynamic ratchet potential, amounting to a composite motor formed from the pulsated-ratchet Brownian motor and the selfphoretic active particle. This composite motor exhibits a directed transport,where thermal noise is actively exploited due to the time-modulated ratchet potential.By extensively exploring the parameter space,we show that the transport velocity of the Janus particle depends sensitively on the modulated frequency of the external potential. Furthermore, the mesoscale simulation method used in the work allows us to study the hydrodynamic effects on the orientation of the active Janus particle and hence its transport,exhibiting a significant polarization of the self-thermophoretic Janus particle in direct contrast to the case of the active Brownian particle.

2. Simulation method and systems

2.1. Solvent

2.2. Self-thermophoretic Janus particle

The colloidal particle is modeled by a single bead that interacts with the solvent via a Lennard-Jones (LJ)-type potential

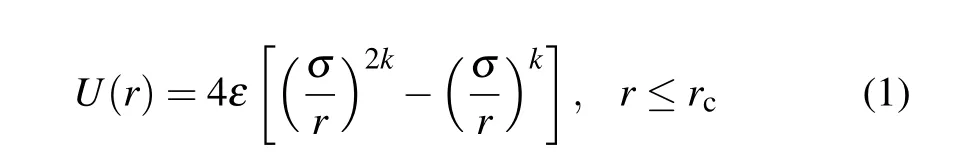
with the potential intensityε=1,the colloidal particle radiusσ=4.0, and the positive integerk=14, which controls the potential stiffness. Here,ris the distance from the bead center to the solvent,withrc=5.3 the cutoff distance.The Janus particle is constructed by defining a body-fixed orientation vectorn(symmetry axis), with its two hemispheres having different physical properties. The forward hemisphere(with the polar angleθ ≤π/2 with respect ton, Fig. 1(a)) is modeled as the heated hemisphere by using local thermostats to heat its surrounding solvent.[38-40]Briefly, the thin layer of fluid around the forward hemisphere is divided into several small areas. For each area, the thermal kinetic energy of solvent is improved by rescaling their velocities relative to the center-ofmass velocity of the element. Outside the thin layer, the energy is locally conserved so that the heat conduction process is physically correct. Experimentally, the Janus particle can heat the surronding solvent under an illumination by coating a light-absorbing material on its heated hemisphere.[26]The input energy is drained from the system by fixing the mean temperature of the solution to a lower value,which is realized by uniformly rescaling the velocities of all the fluid particles relative to the solvent center-of-mass velocity. Since the system is large, this operation hardly affects the particle dynamics. The resulting temperature field is consequently compatible with the heat diffusion equation.

The MPC solvent has an ideal gas equation of state, so the solvent density is lower around the heated hemisphere than the non-heated one. The larger number of particles on the non-heated side produces a stronger attraction. Consequently, the Janus particle self-propels towards the low temperature area, namely, against thenaxis. Moreover, in order to model the rotational diffusion of the colloidal particle, a sticky boundary condition is implemented on the particle surface through a revised bounce-back collision rule.[40]With the system parameters employed in the mesoscale simulation, the self-thermophoretic Janus particle has the selfpropelled velocityvs= 0.018, the rotational diffusion coefficientDr=0.0038,and the translational diffusion coefficientDt=0.015.The simulation box is a rectangle with dimensionsLx×Ly=102×40,where the periodic boundary condition and the stick wall are applied in thexandydirections,respectively.

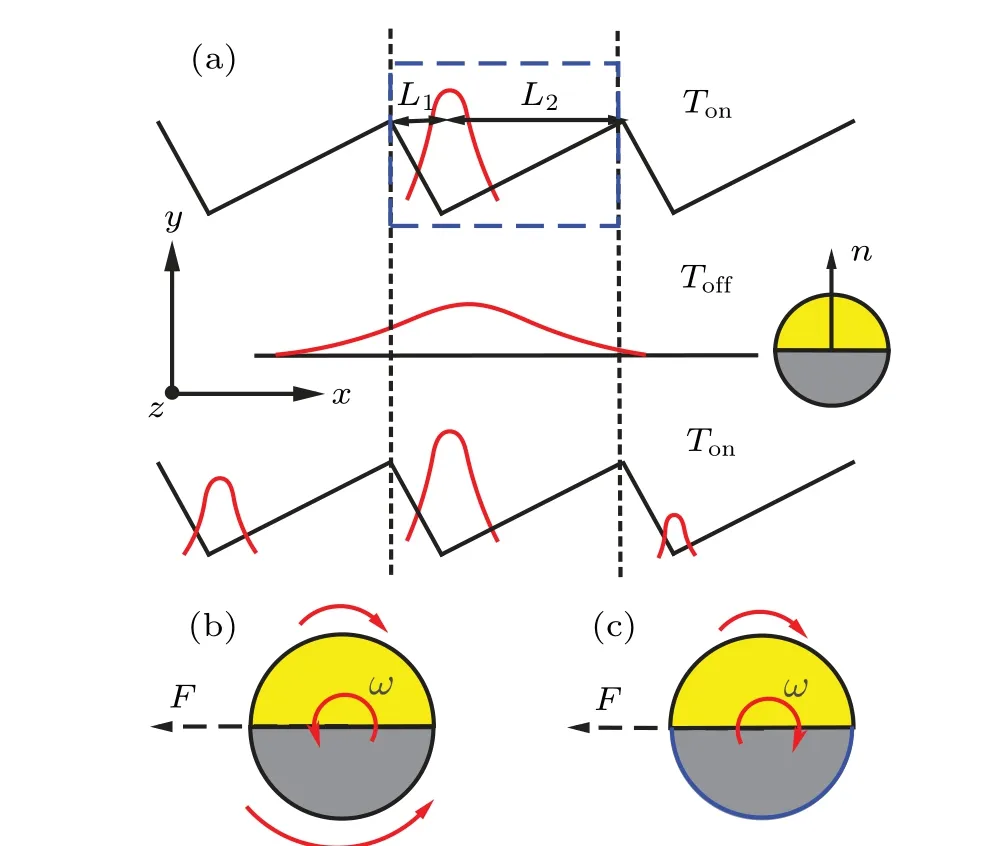
Fig. 1. (a) Schematic diagram of a self-thermophoretic Janus particle in an asymmetric external ratchet potential characterized by two length scales L1 and L2. The self-thermophoretic Janus particle selfpropells against its heated side (yellow hemisphere). The red curves sketch the spatial probability distribution of the active particle with the ratchet potential off or on. (b),(c)Hydrodynamic alignment of the selfthermophoretic Janus particles, moving in the x-direction, induced by asymmetric surface friction(red arrows): (b)corresponds to the case of the stick boundary for the whole particle surface,while(c)corresponds to the slip boundary at the nonheated surface(blue line).

2.3. External ratchet potential

In order to model the pulsated Brownian ratchet that utilizes thermal noise, an external sawtooth-like potentialV(x)is applied to the active Janus particle, with a spatial periodL=5.1 that is comparable to the persistent length of the selfthermophoretic particle. The external potential is spatially asymmetric by skewing the barriers to the right with different ratchet lengthsL1=0.71 andL2=4.39, as sketched in Fig. 1(a). The ratchet potential is constructed in a piecewise manner, with both the potential and its first-order derivative being continuous. Within a repeated unit,the force applied on the colloidal particle due to the ratchet potential has the form

The ratchet potential is time modulated by periodically turning it on and off, with residence timeTonin the on state andToffin the off state (Ttot=Ton+Toffthe modulation period). The strength of the external ratchet force is stronger than the selfthermophoretic force on the Janus particle,Fs=kBTvs/Dt,so that the active Janus particle stays in a close vicinity of the potential minima when the ratchet potential is on.

3. Results and discussion

3.1. Brownian motor with a passive colloidal particle

We first use the mesoscale fluid method to simulate a traditional Brownian motor,with a passive colloidal particle subjected to a periodically varying ratchet potential. Figure 2(a)displays the contour plot of the transport velocity of the Brownian motor, showing that the passive colloidal particle moves to the left(i.e.,toward the steeper potential side)in the range of parameters under study. This result is consistent with the standard pulsated-type Brownian motor[41-43]and can be well understood accordingly. Briefly,when the ratchet potential is on,the passive colloidal particle basically stays in close vicinity of potential minima because the depth of the potential well is much larger thankBT. When the ratchet potential is off,the particle can diffuse freely with a relatively larger probability, crossing the area corresponding to its left-side barrier(the short edge of the sawtooth potential). Consequently, the passive colloidal particle drifts with a negative velocity. The transport velocity is found to sensitively depend on the modulation periodTtotand the residence timeTon.Within an optimal range ofTonandTtot,the Brownian motor can achieve a maximum transport velocity around?0.018. This optimal performance can be easily understood by noticing that for smallTtotor largeTonthe passive particle is difficult to diffuse across the barrier region, while for longTtotor shortTonthe ratchet potential hardly plays a role.

For comparison,we also performed overdamped Brownian dynamics simulations to calculate the contour plot of the Brownian motor transport velocity (Fig. 2(b)), in which the particle diffusion coefficients are imposed to be the same as those in the mesoscale fluid simulation. It is found that the absence of hydrodynamic effects can largely change the transport velocity map of the Brownian micromotor. Particularly,in this case,the optimal transport parameters(TonandTtot)are different from those in the case of the mesoscale fluid simulation.

3.2. Composite micromotor with a self-thermophoretic particle

In this section, we model a composite micromotor by replacing the passive Brownian motor particle with a selfthermophoretic Janus particle, as sketched in Fig. 1. Figure 2(c)depicts the contour plot of the transport velocity of the composite motor. In a wide range of parameters,the composite micromotor drifts along the negativex-direction,similar to the pure Brownian motor. Nevertheless, the maximum transport velocity of the composite micromotor(vtran=?0.021)is larger than that of the Brownian motor. This is mainly because the self-propelled Janus particle can cross more easily the potential barrier region than the passive particle,when the ratchet potential is off.

Interestingly, for smallTtotandTon, the composite micromotor reverses its transport velocity and drifts toward the slanted edge of the ratchet potential. This reversed transport can be understood based on the following fact: the selfthermophoretic force of the Janus particle(Fs=1.2)is much smaller than the external force produced by the steep side of the ratchet potential, but comparable to the strength of the slanted side. Thus the composite micromotor self-propelling along the slanted side of the ratchet potential is dragged back toward the potential minimum only slightly by the short-lived ratchet potential during each on-state. In this case,the persistence length of the active Janus particle(vs/Dr?4.74),which is hardly affected due to the weak slanted-side force and the shortTon,is beyond the length of the slanted side(L2=4.39).Thus, the Janus particle has a non-vanishing probability to cross its right-side barrier. In contrast, the active Janus particle cannot surmount its left-side barrier,since the strong force produced by the steep side of the ratchet potential can rapidly drag the Janus particle back to the potential well during each on-state. As a consequence, the composite micromotor displays a weak positive transport in the narrow range of the modulation parameters.

For comparison, we also determine the transport velocity distribution of the active Brownian particle in a timemodulated ratchet potential by Brownian dynamics simulations with the samevs,DtandDras the composite micromotor in the hydrodynamics simulation, as shown in Fig.2(d). It is found that for smallTtotandTonthe active Brownian particle can also experience a weak transport along thex-direction,although its transport contour plot is different from that of the composite micromotor.

Fig.2. Contour plots of the micromotor transport velocity in the x-direction as a function of the modulation period Ttot and Ton/Ttot. Brownian motor with a passive particle with(a),and without(b)hydrodynamics,(c)composite motor composed of the self-thermophoretic Janus particle,(d)an active Brownian particle moving in a ratchet potential,(e)composite motor with the self-thermophoretic Janus particle having a slip boundary on its non-heated hemisphere. The results in(a), (c), (e)are all obtained by the hybrid mesoscale simulation,while those in(b),(d)are obtained through the Brownian dynamics simulation without explicit solvent.

An important difference between the composite micromotor and the active Brownian particle is reflected by their orientational distributions. The active Brownian particle has a uniform orientational distribution(Fig.3), as the alignment effect is lacking, while the self-thermophoretic Janus paricle tends to align its heated part towards the steep side of the ratchet potential, as shown in Fig. 3, displaying an inhomogeneous orientational distribution. This alignment is hydrodynamic in its origin. Compared to the non-heated part of the Janus particle, the heat part feels a lower fluid viscosity(weaker friction with the solvent)due to the enhanced temperature. As a result of this asymmetric friction the composite micromotor that transports against thex-direction experiences a (restoring) frictional torque that orients the Janus particle against thex-direction, as sketched in Fig. 1(b). In this situation, the self-thermophoretic direction of the Janus particle is opposite to the transport direction of the composite micromotor.

A natural question thus arises whether we can change the hydrodynamic alignment of the self-thermophoretic Janus particle so as to improve the performance of the composite micromotor.This can be in fact easily achieved by modifying the surface properties of the Janus particle. For instance, when the non-heated surface of the Janus particle is a slip boundary,the anisotropic hydrodynamic friction experienced by the composite micromotor drifting against thex-direction will result in a restoring frictional torque[Fig.1(c)],with the stable orientation of the Janus particle pointing along thex-axis, as confirmed by the mesoscale fluid simulation(Fig.3).

For the Janus particle with its non-heated part having a slip boundary, its stable orientation is thus consistent with the transport direction of the composite micromotor. In this case therefore the hydrodynamic alignment effect will enhance the transport of the composite micromotor. Figure 2(e)plots the transport velocity distribution of such a composite micromotor, displaying a higher maximum transport velocityvtran=?0.026. In addition, this maximum transport velocity is close to the superposition of the self-propelling speed of the pure self-thermophoretic particle and the drift speed of the pure Browmian motor under the same ratchet potential.

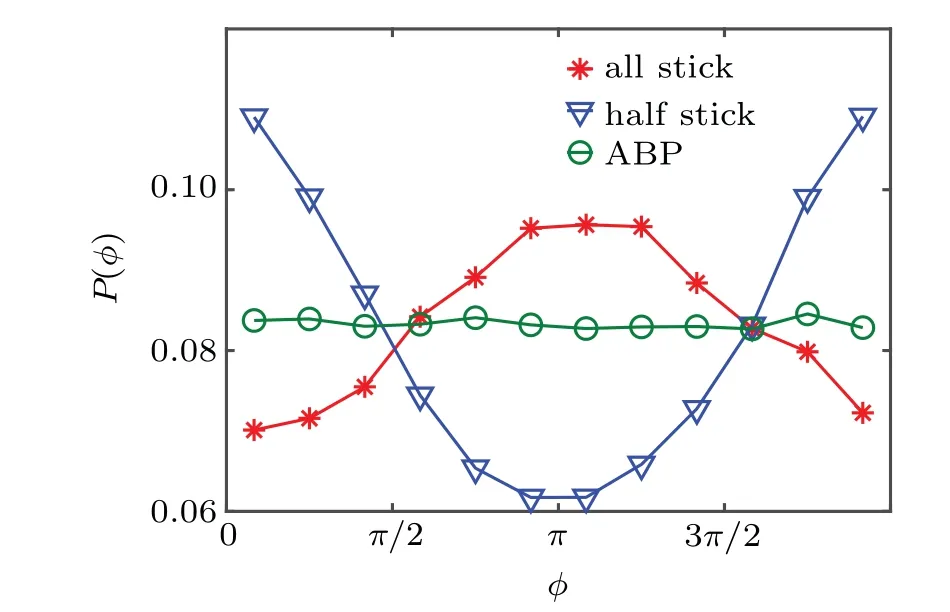
Fig.3.Orientational probability distribution of different active particles in a ratchet potential, with φ the angle between the n and x axes. The simulations are perfomed with Ttot =80 and Ton/Ttot =0.4, for which the particle drifts against the x-direction. The circle refers to the active Brownian particle simulated by the Brownian dynamics method,the cross to the self-thermophoretic particle with the stick surface,and the triangle to the self-thermophoretic particle with the slip boundary for its non-heated part.

4. Conclusion

In this paper, we perform mesoscale dynamics simulations to investigate the transport behaviors of the composite micromotor composed of a self-thermophoretic colloidal particle in a time-modulated ratchet potential. It is found that the composite micromotor exhibits a unidirectional transport,whose direction can be reversed by tuning the modulation frequency of the ratchet potential. Moreover, due to anisotropic surface friction,the active Janus particle exhibits a significant hydrodynamic alignment, in stark contrast to the traditional active Brownian particle. With the alignment effect,the composite motor is able to achieve a maximum transport velocity even close to the superposition of the self-propelling speed of the pure self-thermophoretic particle and the drift speed of the pure Browmian motor.Given the potential applications of selfpropelled microswimmers and the ubiquity of thermal fluctuation, our work provides an interesting attempt to actively utilize thermal fluctuations in the performance of microswimmers.