Effect of pulse duration on generation of attosecond pulse with coherent wake emission*

Siyu Chen(陳思宇) Zhinan Zeng(曾志男) and Ruxin Li(李儒新)

1School of Physical Science and Technology,ShanghaiTech University,Shanghai 201210,China

2State Key Laboratory of High Field Laser Physics,Shanghai Institute of Optics and Fine Mechanics,Chinese Academy of Sciences,Shanghai 201800,China

Keywords: coherent wake emission,carrier envelope,attosecond pulse,high-order harmonics

1. Introduction

Laser-plasma interaction is one of the promising methods for high-order harmonics generation(HHG)with high conversion efficiency. Research of generation and basic characteristics of high-order harmonics is important for a broad application prospect of light sources with extreme properties,such as attosecond pulse,[1,2]extreme ultraviolet light sources,and soft x-ray monochromatic light sources.[3,4]In addition,studying the dynamics of high-order harmonics generated by laserplasma interaction is of great scientific significance for different physical mechanisms of HHG,[5]temporal domain characteristics of attosecond pulse,[6]spectral domain characteristics of HHG,[7]frequency chirp characteristics of high-order harmonics.[8]

The interaction between the super-intense laser and the plasma produces high-order harmonics with different physical mechanisms.[9]Most of these physical mechanisms occur in the range of laser intensityIλ2l>1.37×1018μm2·W/cm2.However, one of these physical mechanisms, coherent wake emission (CWE), has a certain peculiarity. Qu′er′eet al.have carried out detailed research on CWE and carefully demonstrated that within each laser cycle,Brunel electron[10]generated by the laser causes plasma oscillation,and phase matching occurs locally to generate high-order harmonics. The maximum frequency of the generated high-order harmonics is limited by the local oscillation frequencyωpeof overdense plasma.[11]In order to offer a laser electric field component perpendicular to the plasma surface, it is required to use the p-polarized laser, and it is necessary to generate the maximum plasma oscillation frequency within the limited plasma layer on the front surface of the plasma.[12-14]The CWE process mainly occurs under the condition ofIλ2l<1.37×1018μm2·W/cm2. At such laser intensity,relativistic effect is generally weak.

In recent years, research on CWE has gradually increased.In 2010,Thauryet al.described the theoretical model and calculated the motion of Brunel electron, the transverse current generated in the high-density plasma, the plasma oscillation and the high-order harmonic emission time under the interaction between the long-pulse-width laser and plasma.[15]Through theoretical calculation and function fitting,Malvacheet al.and Qu′er′eet al.analyzed the influence of different laser periods on the emission time of attosecond pulses in CWE mechanism.[16,17]However, previous studies mainly focused on the characteristics of CWE attosecond pulse and HHG analytically in the form of plane waves, and ignored the influence of limited laser pulse envelope. As we know, for laserplasma interaction with short pulse,laser periodic electric field changes by its envelope and laser carrier-envelope phase. This may cause the influence on the Brunel electron motion under different carrier-envelope phases and the laser pulse width,and further influence on overdense plasma oscillation frequency.Furthermore,it results in pulse output delay and the chirp characteristics of high-order harmonics.

In this work, we investigate the influence of laser pulse duration on attosecond pulse chirp in CWE based on particlein-cell (PIC) code and some analytical results. We find that for a few-cycle pulse, the chirp of the high-order harmonics corresponding to a single attosecond pulse generated by one laser cycle becomes very prominent because of the CEP effect on the motion of Brunel electron.

2. Effect of different full widths at half maximum of the laser pulse

In the CWE process, when a laser interacts with the plasma, the electrons of the plasma surface are firstly pulled out of the plasma into the vacuum by the strong laser electric field. Then, after the laser field changes the sign, the electrons change the direction of motion and are accelerated back to the high-density plasma region. These clumped electrons penetrate the front surface of the plasma and excite the plasma oscillation by the wake field of the electron beam. In this process,the electron returning velocity and density distribution determine the maximum oscillation frequency of overdense plasma.[18]We describe the time related to the movement of electrons during the laser plasma interaction,as shown in Fig.1. The generation time of the electron entering the vacuum is set to bet0, and under the action of the reverse laser electric field force,the return time of the electron back to the plasma critical density region is set to betr, and the time for election reaching some positionxωin the overdense plasma istc.

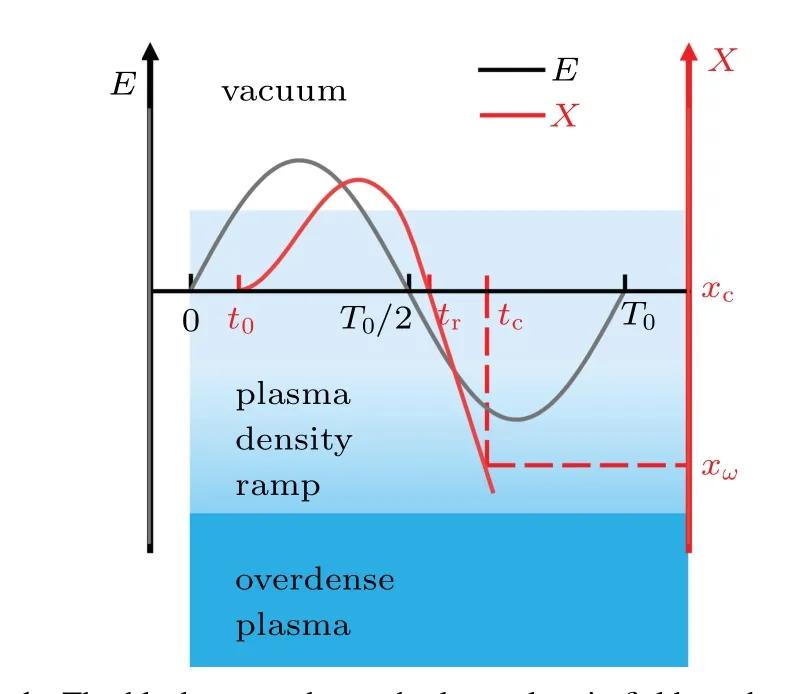
Fig. 1. The black curve shows the laser electric field on the electron with time in one laser cycle. The red curve shows the electron movement to the overdense plasma region xω. Several key times are marked in the figure, including the return time tr when the electron enters the vacuum region and falls back to the critical density,and the time tc when the particle passes through the plasma density gradient and reaches the overdense plasma coordinate xω.

On the plasma surface, Brunel electrons pulled out att0are acted by laser electric fieldELand the electrostatic field.According to Brunel’s point of view,[10]we can approximately consider that the interaction force between electrons in vacuum is 0,and the electrostatic field is constant and oppositely equals the laser electric field att0,and the following equation can be obtained:[17]

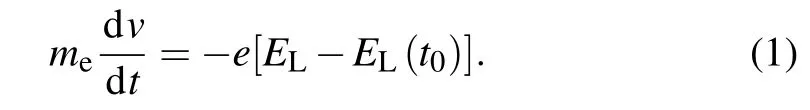
For a short pulse with a certain CEP, the influence of carrier envelope on the laser electric field in each cycle cannot be ignored here. The laser electric field is expressed as

In the following,we discuss the influence of laser pulse duration on the emission delay of attosecond pulse and the chirp characteristic of high-order harmonics with Eqs. (5) and (6).According to the analysis in Ref. [15], the emission time of attosecond pulse is decided by the speed of electrons in the high-density plasma, the position of phase matching, and the scale of plasma density gradient. Based on these results, we calculate electron velocities of different laser pulse duration,and analyze the influence of the laser FWHM on the attosecond pulse emission delay and harmonic chirp characteristics.The laser electric field cannot enter the overdense plasma. It is generally believed that after electrons return back to the critical density plasma, they will enter the overdense plasma and propagate at a constant speedVFWHM(tr)to the positionxωexciting the plasma oscillation of frequencyω. The arrival time istc,which can be written as[15]

wheretcis the unit of laser periodTL, as shown in Fig. 1.With the increase of the laser amplitude, the electron returning speed increases,and the emission time of attosecond pulse decreases.[19]Therefore, the intensity envelopeI(t) of the laser pulse directly leads to the inhomogeneous emission of the attosecond pulse sequence. The influence of laser FWHM on attosecond pulse sequence and the chirp properties of high order harmonics are investigated in this work.

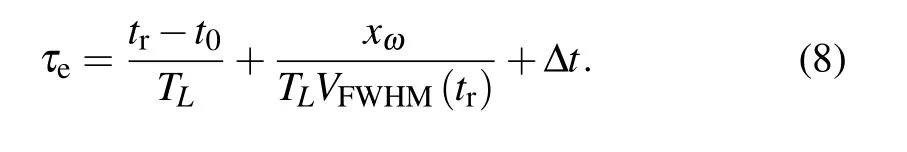
According to Eqs.(7)and(26)in Ref.[15],the total time to generate attosecond pulse starting from electron into vacuum from the plasma surface can be written as Here, ?t=[2L(1/c+1/vp)]/TLis the time interval between the excitation of plasma oscillations and the attosecond pulse emission time. We substitute the electron velocityv(tr) into Eq.(8),the result is shown in Fig.2(a).

According to Ref. [16], the emission time of attosecond pulse of each laser cycle can be fitted by an analytical formula.With the decrease of the pulse duration,the effect of the pulse envelope becomes important because the increase of electric field from 0 to the peak will be more rapid, which induces the change of attosecond pulse emission timete, as shown in Fig.2(b).

Fig.2. The output delay τe of attosecond pulse generated by laser pulse of FWHM=10, 5, 3, 2, respectively. The unit of FWHM is laser cycle TL. (a)Theoretical simulation result and PIC simulation result. The Gaussian curves are laser envelope of different FWHMs. Plasma of maximum density 120nc (nc the critical density at the laser frequency)is driven by laser pulse with different Gaussian envelopes at 45° incidence, and the exponential density gradient scale length is λ/100. (b)The chirp of individual CWE harmonics obtained from PIC simulations.The unit of FWHM is laser cycle TL.

The spatial phase characteristics of CWE high-order harmonics are also determined by the time offset of the attosecond pulse. Therefore,in order to investigate the chirp characteristics of CWE high-order harmonics under the influence of pulses with Gaussian intensity envelope,[16]the time interval of two adjacent attosecond pulses can be calculated by

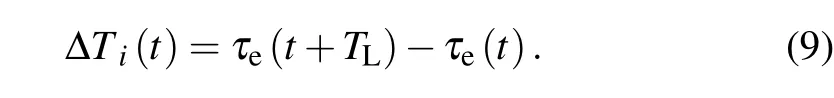
As ?Ti(t)increases with timet,it leads to a negative chirp of the individual harmonic.[17]The emission delayτwill introduce a phase forqthharmonic as eiωq?Ti(t),and the frequency chirp of the harmonic orderqisωq?Ti(t). Thus, the chirp is proportional to the harmonic order. The PIC simulation result shows that the attosecond chirp from the 2nd harmonic to the 8th harmonic around the pulse crest is linear dependence, as shown in Fig. 2(b). From Fig. 2(a), the emission delays for different laser pulse FWHM are different. Especially, when the FWHM=2, the emission delay difference of attosecond pulse is slightly larger than others, which induces a clearly larger harmonic frequency chirp in Fig.2(b)(green line).

3. Effect of different carrier envelope phases of the laser pulse

There is another problem that, if the laser pulse is very short, e.g., shorter than 3 laser cycles, the effect of CEP may be distinct. Then the chirp characteristics of harmonics may not only depend on the pulse width of the laser, but also be affected by laser CEP.In order to investigate the influence of laser CEP on the generation of high-order harmonics,we need to calculate the motion of electrons starting from Eqs.(3)and(4), and then calculate the chirp characteristics of high-order harmonics. Therefore, to get the relationship betweenv(tr)andx(tr)under different laser pulse CEPs intuitively,we firstly draw the trajectory and velocity of the electrons driven by different CEP laser pulses,as shown in Fig.3.

Figures 3(i)-3(l)show the movement of the different electron trajectories driven by the laser pulse with different CEPs,part of Brunel electrons cannot return to plasma in a cycle.The electrons returning to the plasma critical density have speedv(tr)in distribution dramatically dependent on laser CEP.This can be directly related to the time of the reverse electric field working on the electron. The electrons having an earlier excitation time will experience longer positive electric field,which leads to a larger electron energy and ultimately cannot return to the plasma. The electrons being pulled out later will experience a longer reverse electric field acceleration,returning back to the plasma with a higher speed.

Next, we discuss the motion of Brunel electrons as they pass through the critical density region of the plasma. After the electron beam enters the overdense plasma, due to the shielding effect on the laser electric field,the electrons can be considered moving at a uniform speed with the return velocityv(tr). Because electrons reach the critical density later with higher speed,the trajectories of electrons in the overdense area will cross to a certain extent. To describe the overall motion status of electrons well,we can refer to the trajectories of electron density peaks(red dashed curve)as shown in Fig.4.

For those electrons returning back the plasma surface around the timetrwith trajectories across at a given positionx=xc,we can obtain[15]

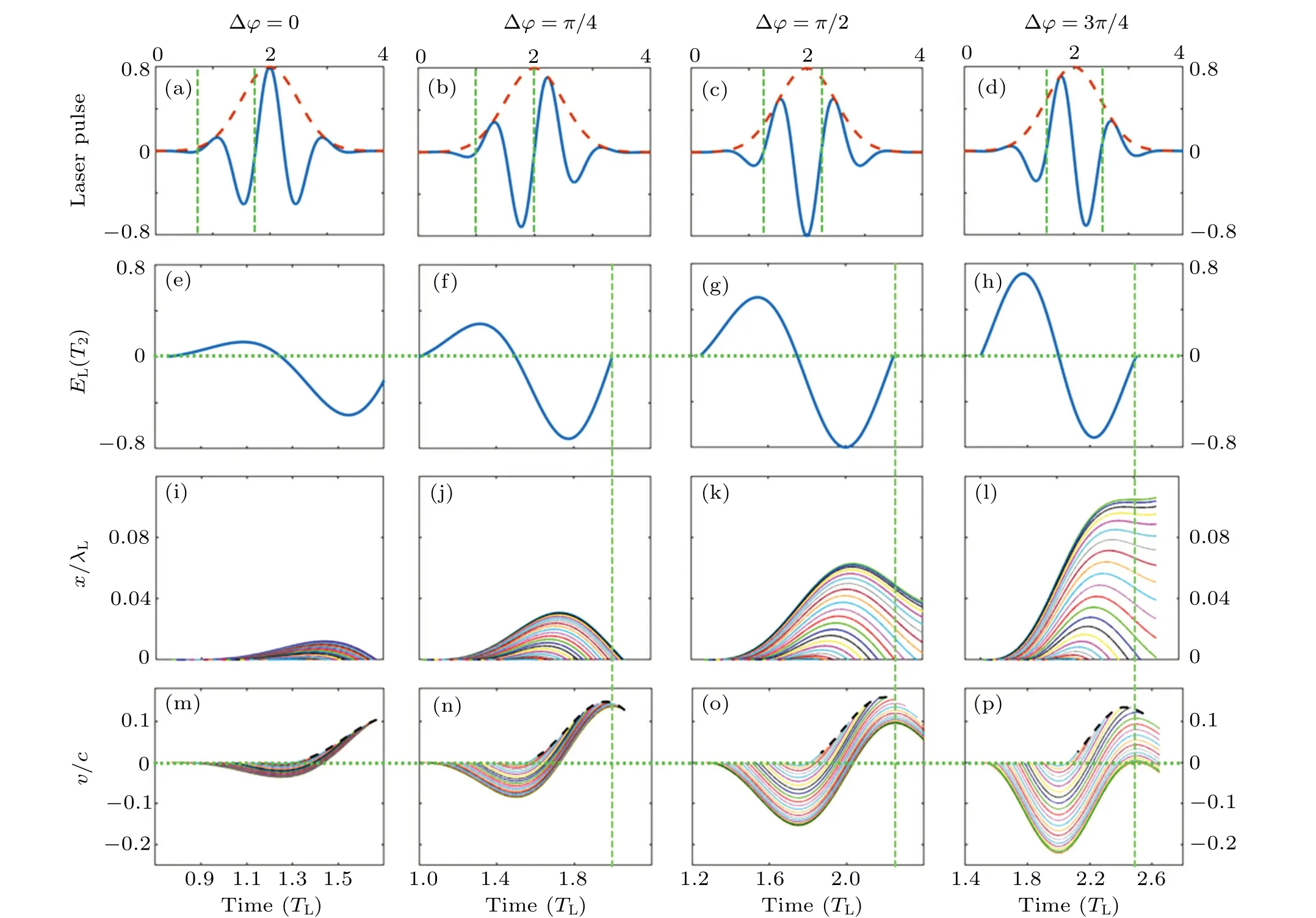
Fig.3. Laser pulses with the CEP(a)? =0,(b)? =π/4,(c)? =π/2,and(d)? =3π/4;(e)-(h)the corresponding laser electric fields of the second laser period;(i)-(l)the corresponding displacement x(τ)of Brunel electron movement from the plasma surface into vacuum,then back to the plasma surface; (m)-(p)the corresponding velocities v(τ)of Brunel electrons as a function of time, where the thick black dotted lines are the return velocities v(tr)of different electrons returning to the plasma surface.

Fig. 4. Trajectories of Brunel electrons traveling in high-density plasma. The red dashed line shows the trajectory of the electron density peak xc.

Then the motion of electron density peak can be obtained,as the red dashed curve in Fig.4. In order to discuss the CEP influence on the movement of electron density peak, a set of relationshipsx?(t)can be obtained,as shown in Fig.5(a). The velocity of electron density peakv?(t)under different CEPs is calculated by

The calculated curves are shown in Fig.5(b).According to the curves in Fig. 5(b), there exists an obvious difference for the velocityv?(t). At some specific positionxc,we can calculate the velocityvp(?)[15]of electron density peak under different CEPs by

The density peak velocities at some specific positionxcwith different laser pulse widths are shown in Fig.6(a). For a fewcycle laser pulse,the electron density peak has obvious maximum speed at some CEP,while for multi-cycle laser pulse,the electron density peak velocity with different CEPs tends to a constant value. As the CEP increases in the interval 0-3π/4,the electron density peak velocityvp(?)increases at first and then decreases. Moreover, this change is very distinct for a few-cycle laser pulse.

Next, we discuss the influence of the laser CEP on the maximum emission frequency which can be achieved in one cycleT,and spectral chirp characteristics.

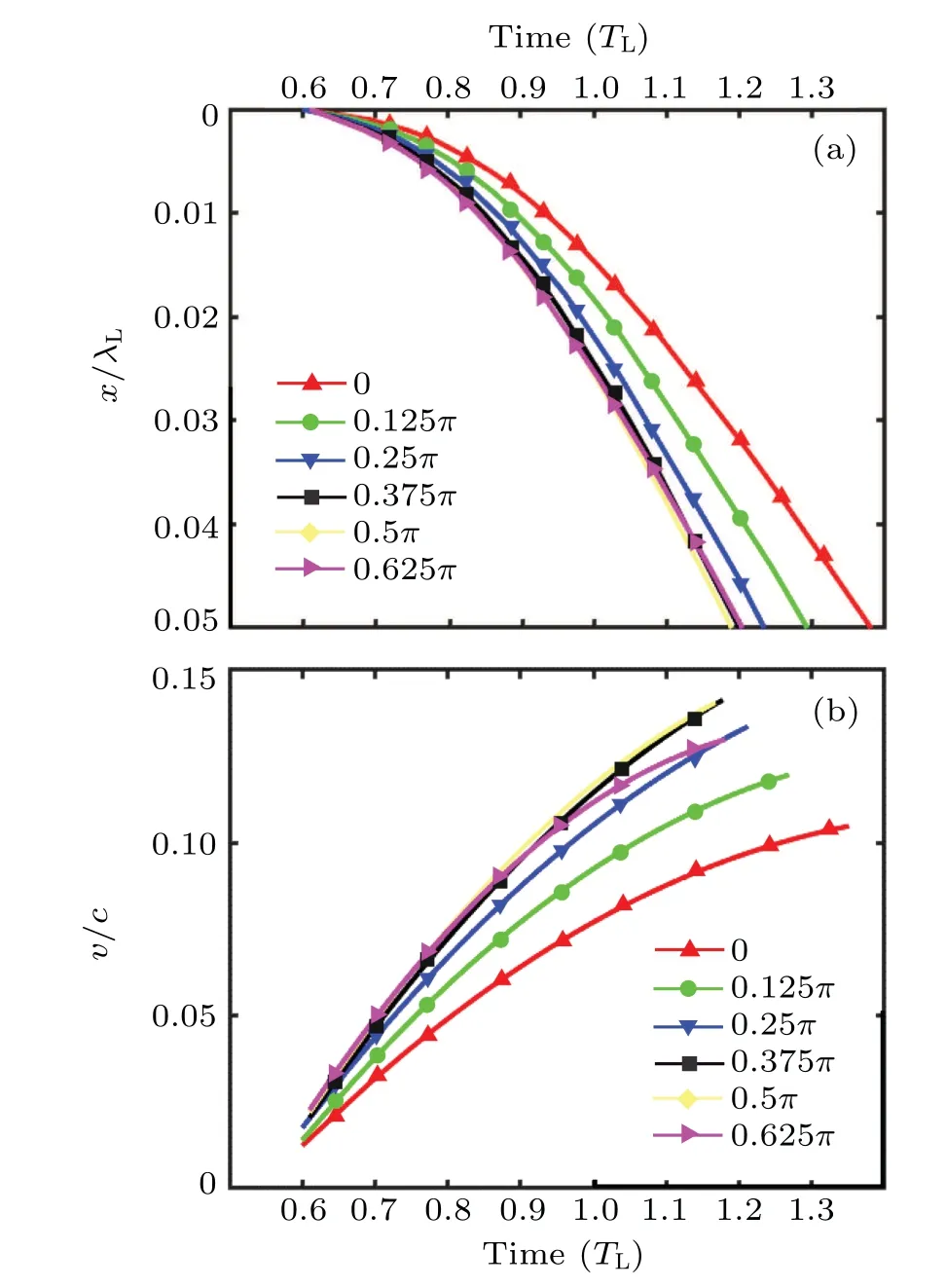
Fig.5. (a)Trajectories of electron density peaks x?(t)in high density plasma under different CEPs. (b)The velocity of electron density peak v?(t)in high density plasma under different CEPs. The horizontal axis is the normalized time in TL.

The maximum emission frequency is decided by the plasma frequencyωp(x)=ωL·exp(x/2L). In a laser cycle of different CEPs,we can calculate the maximum distance in which the electron can propagate:

Thus,according to Fig.6(a),if only considering one cycleT,we can reachx?max≈x0.625π=0.028λL,and if the scale length of the plasma density gradient is set toλL/100,then the resulting plasma frequency will beωp≤8ωL. Thus, for the CWE with few-cycle laser,the CEP of laser needs to be controlled,the gradient scale length is equally significant.For the chirp of the emitted harmonics,we take the 8th harmonic as an example for calculation and analysis. As shown above, laser CEP will affect the emission time. For a few-cycle pulse, the 8th harmonic chirp changes as shown in Fig. 6(b). For the effect of the laser CEP,when the few-cycle pulse laser interacts with the plasma,the harmonic frequency generated by a single cycle will shift. As shown in Fig. 6(a), compared with longpulse lasers,the electron density peak velocity of the few-cycle laser is smaller,and the changes of the harmonic chirp become more pronounced. Although we take 8thharmonic as an example here, the dynamics of Brunel electrons can always be described universally by the above equations and their trajectories look like that shown in Fig. 3 even for different laser intensities, which will induce the similar result for other harmonics.

Fig. 6. (a) Velocity of electron density peak under different envelope FWHMs in units of laser cycle TL. (b)The chirp parameter of CWE 8th harmonic under the envelope at FWHM=2,1.5,1.

4. Conclusion

In summary, the attosecond pulse produced by CWE is directly determined by the motion of Brunel electrons and the plasma density. Because the laser pulse envelope affects the laser electric field in each optical cycle,and then affects the return velocityv(tr)of Brunel electrons in each optical cycle,the variation of the attosecond pulse emission time in each optical cycle leads to the chirp characteristic of the CWE high-order harmonics. The PIC simulation shows different results with the analytical result on both front and rear edge of the short laser pulse. For a shorter few-cycle pulse,the chirp characteristics of the high-order harmonics will be further affected by the laser CEP.