2020年高考全國Ⅲ卷理科第20題的解答與拓展
林國紅
(廣東省佛山市樂從中學 528315)
一、題目呈現
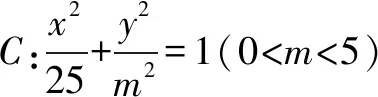
(1)求C的方程;
(2)若點P在C上,點Q在直線x=6上,且|BP|=|BQ|,BP⊥BQ,求△APQ的面積.
由于問題(1)較為簡單,本文不作討論,下面對問題(2)進行解答與探究拓展.
二、解法探究
分析由已知可得點B是定點,可考慮設P(x0,y0),Q(6,n),通過參數將題目的條件進行翻譯與轉化.
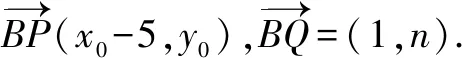
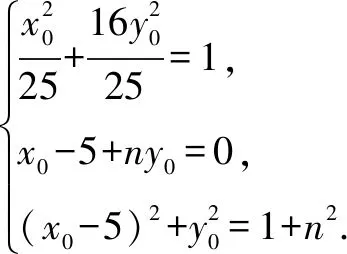
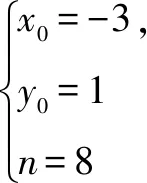
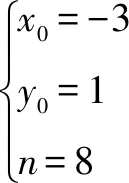
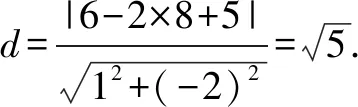
分析由題意,點P由直線BP與橢圓C確定,點Q由直線BQ與直線x=6確定,結合已知條件,利用直線BP的斜率k作為參數將題目的條件進行翻譯與轉化.
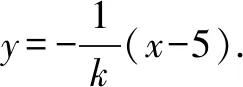
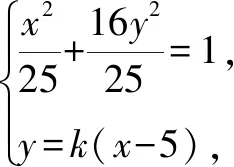
整理,得(1+16k2)x2-160k2x+(400k2-25)=0.
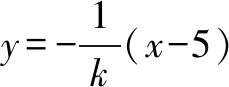
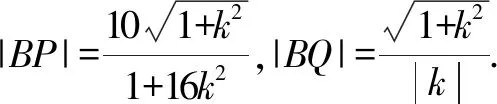
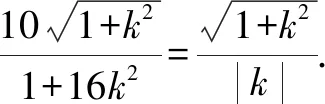
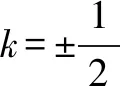
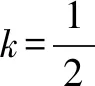
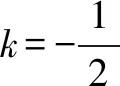
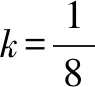
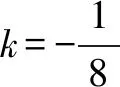
以下同解法1.
分析由條件|BP|=|BQ|,BP⊥BQ,可知由點P的坐標可以確定點Q的坐標,反之亦然.由于點Q的橫坐標為6,故可用點Q的坐標來確定點P的坐標.仍然用斜率作為參數將題目的條件進行翻譯與轉化.
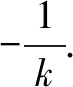
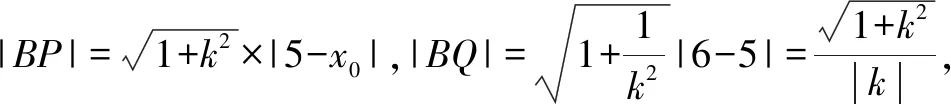
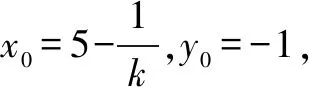
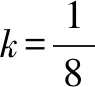
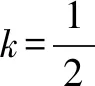
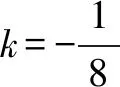
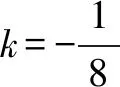
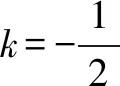
以下同解法1.
分析由橢圓的對稱性,不妨設點P,Q在x軸上方.如圖1,過點P作x軸垂線,垂足為點M,設x=6與x軸交于點N,由△PMB≌△BNQ,可求得點P坐標以及直線AQ的方程,根據點到直線距離公式和兩點間的距離公式,即可求得C的面積.
解法4(平面幾何角度)由橢圓的對稱性,不妨設點P,Q在x軸上方.因為點P在C上,點Q在直線x=6上,且|BP|=|BQ|,BP⊥BQ,過點P作x軸垂線,垂足為點M,設x=6與x軸交于點N,如圖1.
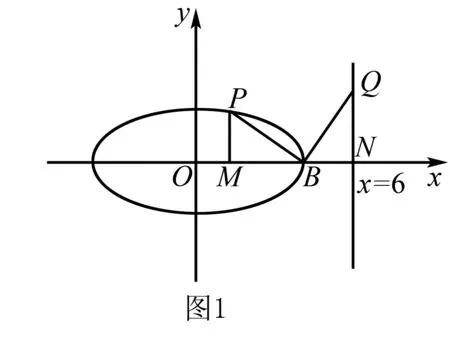
由于|BP|=|BQ|,BP⊥BQ,∠PMB=∠QNB=90°,又因∠PBM+∠QBN=90°,∠BQN+∠QBN=90°,故∠PBM=∠BQN,所以△PMB≌△BNQ.
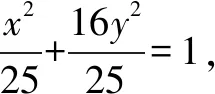
所以|PM|=|BN|=6-5=1.
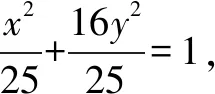
①當點P為(3,1)時,故|MB|=5-3=2.
因為△PMB≌△BNQ,所以|MB|=|NQ|=2,可得點Q為(6,2),如圖2.
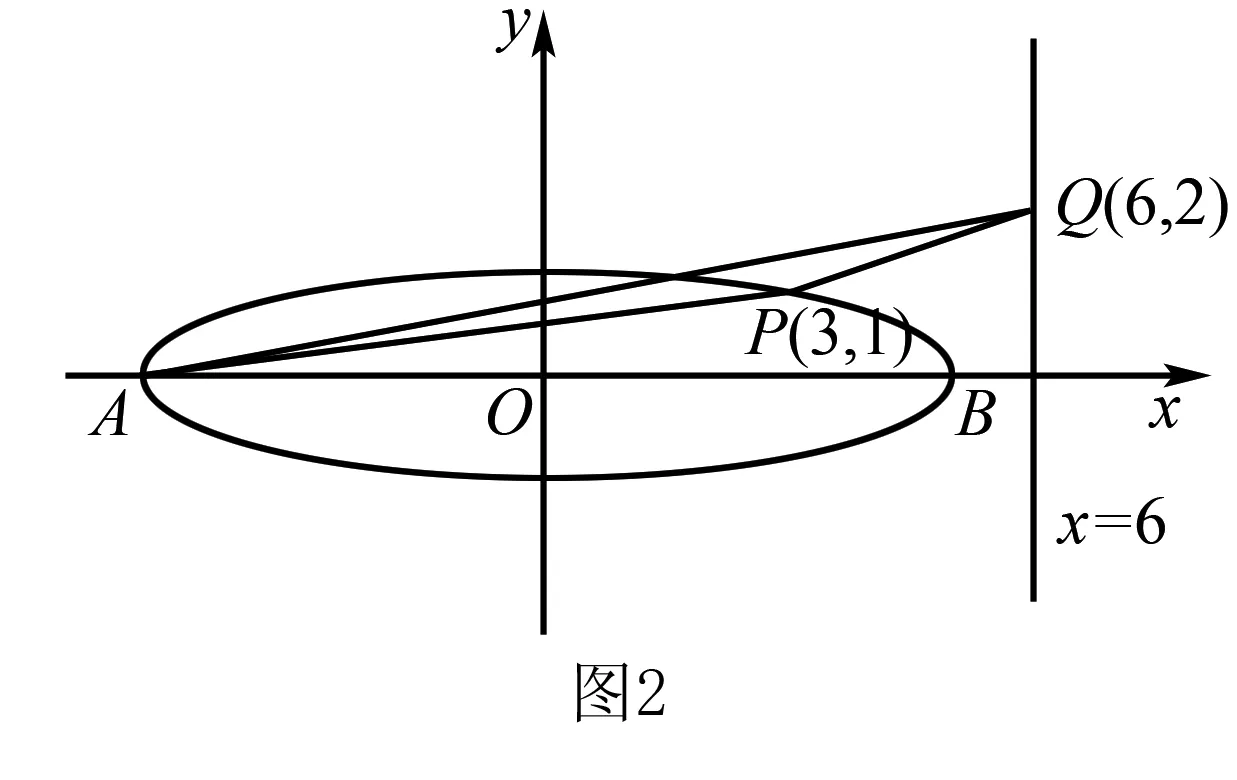
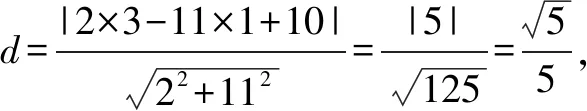
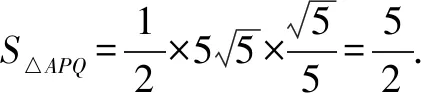
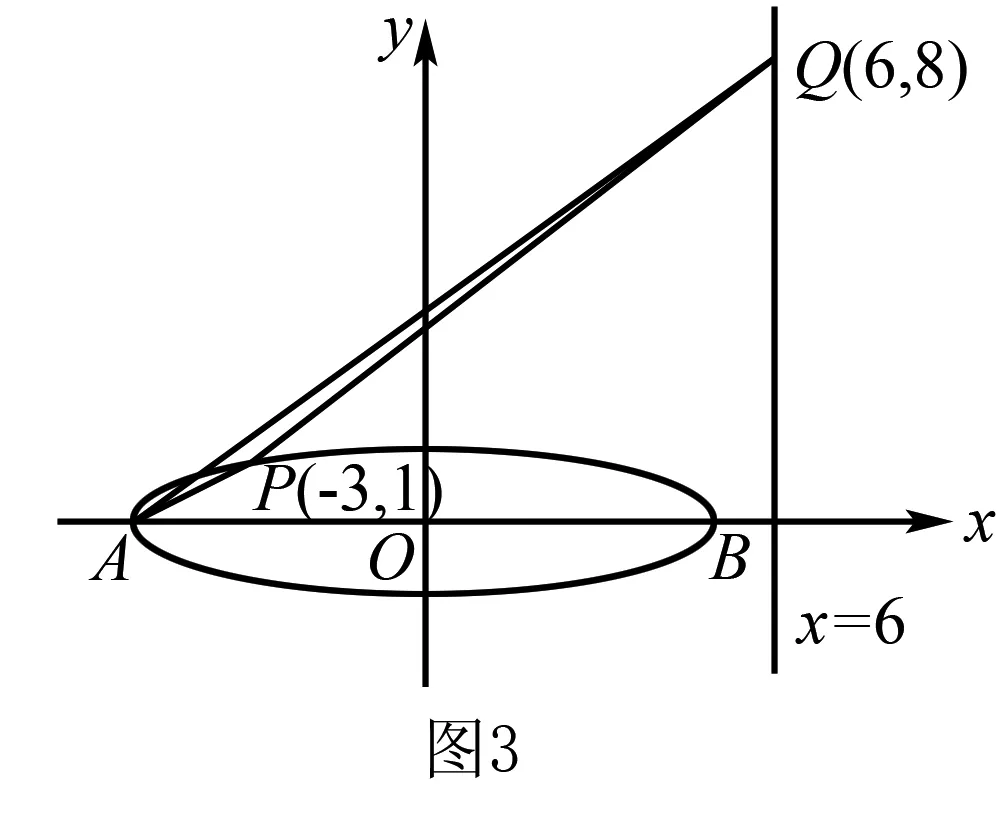
②當點P為(-3,1)時,故|MB|=5+3=8.因為△PMB≌△BNQ,所以|MB|=|NQ|=8,可得點Q為(6,8),如圖3.
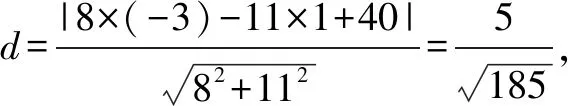
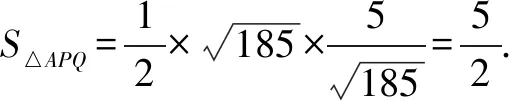
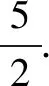
三、試題推廣
將考題一般化,可以得到如下結論:

證明由橢圓的對稱性,不妨設點P,Q在x軸上方,設P(xP,yP),Q(k,yQ).因為點P在C上,點Q在直線x=k上,且|BP|=t|BQ|,BP⊥BQ,過點P作x軸垂線,垂足為點M,設x=k與x軸交于點N,如圖4.
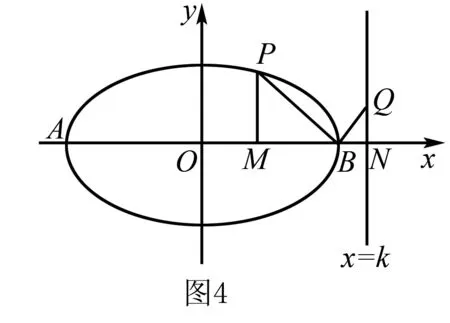
由于|BP|=|BQ|,BP⊥BQ,∠PMB=∠QNB=90°,又因為∠PBM+∠QBN=90°,∠BQN+∠QBN=90°,故∠PBM=∠BQN,所以△PMB∽△BNQ.
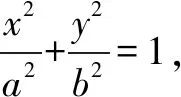
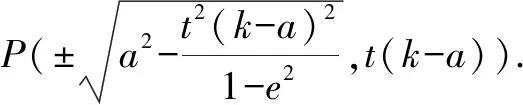

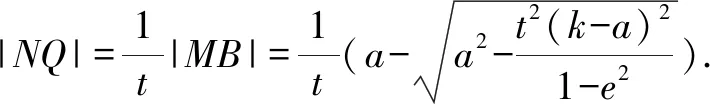
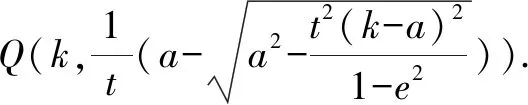
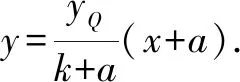
整理,得yQx-(k+a)y+yQa=0,
即yQ(x+a)-(k+a)y=0.
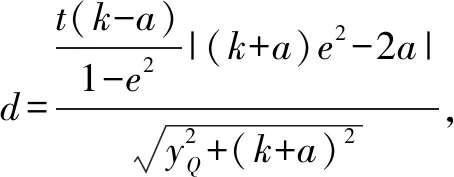
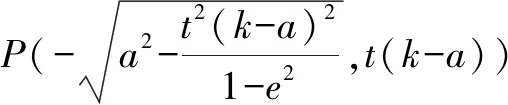
四、類比拓展
經探究,在雙曲線中也有類似的結論:
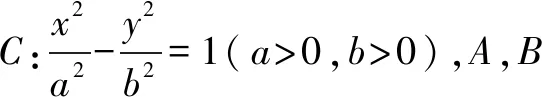
學數學離不開解題,對于一道優秀的試題,應該在獲得解答的基礎上,多角度展開嘗試與聯想,借助題目,探索隱藏在題目背后的奧秘,力求擴大戰果.從特殊到一般的數學思想是解析幾何中數學發現的重要手段,只有養成多思善想、舉一反三,鉆研到底的學習習慣,才能在學習中獲得無窮的樂趣,使思維得到發展.

