例談不等式解法常見的逆用
杜紅全
(甘肅省康縣教育局教研室 746500)
對于已知不等式的解集求不等式的相關參數的取值范圍等問題,解題時,應從不等式解的結構入手,得出相關參數所滿足的條件,進而求解.
一、已知不等式的解集求參數的值

分析本題是解不等式過程的逆向應用,可由解集出發,逆向分析,找出a,b之間的關系式即可.


二、已知不等式的解集求解另一個不等式的解集

分析由已知不等式的解集確定系數的取值情況后,再解所求不等式.

點評求解本題的關鍵是根據不等式的解集,利用根與系數的關系把b,c用含a的式子表示出來,將不等式cx2+bx+a<0轉化為不等式2x2+5x-3<0.
三、已知不等式的解集求參數之比
例3 設a>0,不等式|ax+b| A.1∶2∶3 B.2∶1∶3 C.3∶1∶2 D.3∶2∶1 分析根據題目所給不等式的解集,可將參數b,c用含a的式子表示出來,進而求得a∶b∶c的值. 由①+②,得2c=3a;由①-②,得2b=a. 所以a∶b∶c=2∶1∶3.故選B. 例4 若不等式|x-4|+|3-x| 分析根據題目所給不等式進行分段討論,求出滿足條件a的取值范圍. 綜合①②③可知,當a>1時,原不等式有解,當0 點評求解本題的關鍵是利用分類討論的數學思想方法. 總之 ,已知不等式的解集求參數,此類題常常是利用不等式與相應的方程關系來解題,即轉化為相應方程對應的根,運用根與系數的關系來解題.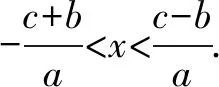
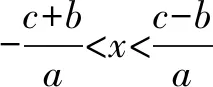
四、已知不等式的解集求參數的取值范圍


