橢圓中的斜率定值問題研究

謝賢祖

(華南師大附中汕尾學校 516600)

圓錐曲線題型多樣，結論眾多，下面筆者先提供常見結論1和結論2，再設計一系列題組，通過例題的分析與變式，總結解決問題的通性通法，希望對高三復習備考有所幫助.限于篇幅，對于一些比較容易的例題，只提供思路，留給讀者自己研究，詳細解答略.

一、證明斜率之積(比)為定值

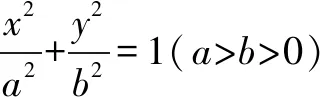
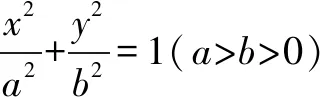
①

總結通過以上例題可以發現，只要已知條件符合結論1和結論2的使用前提，我們便可以利用這兩個結論為我們解題“探路”，但并不是所有的斜率定值題型都可以套用結論，下面看難度更大的例4.

二、由斜率之積(和)為定值，證直線過定點

(1+2k2)x2+4kmx+2m2-6=0

由AM⊥AN，得kAM·kAN=-1.

代入坐標，整理,得(k2+1)x1x2+(km-k+2)(x1+x2)+(m-1)2+4=0.

借助韋達定理，得(2k+m-1)(2k+3m+1)=0.

①

總結(1)對于例7，由于先發現kBD·kBC為定值，所以根據結論2，可以預測直線CD過定點，再用通性通法寫過程，則輕松很多；(2)通過以上例題可以發現，對于橢圓的內接三角形，只要有兩邊的斜率之積或者斜率之和為定值，則第三邊所在直線會過定點.

總結(1)例8的題設條件與例4完全相同，解題思想一樣.對于無法借助斜率之積或斜率之和為定值來解決的難題，如例8，唯有利用通性通法硬算破解；(2)可以總結解題經驗：只要點E和F是x軸上的定點，直線MN必會過定點.

通過以上8道例題的分析可以發現，斜率之積(和)為定值和直線過定點經常具有等價性，有時彼此之間可以互相推導，但不是絕對.我們可以粗略地總結如下經驗：直線過定點，斜率之積(或和)為定值；斜率之積(或和)為定值，則直線過定點.這樣可以幫助我們預判解題之路.而對于像例4和例8這樣的無結論可直接套用的題目，唯有通性通法是“王道”.最后提供兩個變式題供讀者選用.