高中物理解題的整體法和隔離法的應用研究
龐亞茹
(甘肅省慶陽第一中學 745000)
高中物理的解題方法是學生學習相關物理知識的重要障礙,大部分學生因為無法正確的運用相關方法實施解題,就會影響到學生考試成績的提高.因此,物理教師在具體教學時,需注重教學方式的轉變,不能太過于注重對物理知識進行機械記憶,需注重教學方法與解題技巧的講解.方法作為溝通思想、知識、能力的橋梁,由此可知,物理方法也是物理思想的實際表現,學生只有學會了方法,學生的問題分析以及解決能力也就能得到相應的提高,并促進物理成績的不斷提高.而整體法與隔離法作為物理解題過程中的重要方法,教師通過該方法的講解,通常能夠使學生分析與解決相關物理問題的能力得到有效提高.
一、整體法與隔離法概述
整體法主要將涉及到的多個物體或過程看作為整體,對解題思路進行思考.在只涉及到系統,而沒有涉及到系統內的運動、力與其他特殊狀況下,可充分考慮整體法,以促使整體法的教學優勢得到充分發揮.整體法通常能分成兩類,第一,整體研究的物體系統;第二,整體研究的運動全過程,而忽略當中的細節.
隔離法主要將物理問題的相關對象或者狀態、過程由系統或整個過程當中隔離出的實施研究的思維方式.如果想搞清楚系統當中某個物體的具體受力以及運動的相關信息,此時,就能運用隔離法.隔離法通常有兩種狀況,第一,對研究對象實施隔離分析;第二,對研究的過程實施分段研究.
高中物理的解題中,通過隔離法與整體法的運用,對高中物理的相關問題進行解決,不僅可以使學生形成創新性的探究思維,而且還能滿足當前教育的改革方向,從而使學生的解題效率得到有效提高.
二、高中物理解題的整體法和隔離法的應用策略
1.平衡狀態的應用
如圖1所示,質量為5 kg的長方體木塊放在質量為10 kg的粗糙三角形物體的斜面上,斜面與地面夾角30度.現在給小長方體木塊一個沿斜面向上,大小為30N的力F,長方體木塊沿斜面做勻速運動,這一過程中三角形物體保持靜止.那么,地面對三角形斜面物體的支持力和摩擦力各是多少?

圖1
解析本題是一道斜面物體受力分析的試題,在解題方法上,可以將兩個物體進行單獨隔離分析,也可以進行整體分析.
隔離法:先對長方體木塊進行受力分析,其受沿斜面的推力F,重力G,摩擦力f,和支持力N,如圖2(a);三角形物體受重力G1,長方體木塊的摩擦力f1,地面的摩擦力f2,地面支持力N1,如圖2(b).

圖2
由圖2(a)可得:N=Gcos30°,F=f+Gsin30°
由圖2(b)可得N1+f1sin30°=G1+Ncos30°,f1=f,
f2=f1cos30°+Nsin30°

由此可得,在進行試題分析的時候,可以根據已知條件選擇合適的方法,往往可以達到事半功倍的效果.
2.牛頓運動定律的應用
如圖3,水平地面上有三個靠在一起的物塊P、Q和R,質量分別為m、2m和3m,物塊與地面間的動摩擦因數都為μ.用大小為F的水平外力推動物塊P,記R和Q之間相互作用力與Q與P之間相互作用力大小之比為k.下列判斷正確的是( ).

圖3

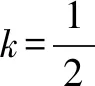


解決本題首先用整體法求出三個物塊的加速度,當各物體的運動狀態相同時,可選用整體法然后再隔離各個物塊進行分析求解,先用整體法求解加速度使得這個題簡單了許多.對較復雜的問題,通常需要多次選取研究對象,交替應用整體法與隔離法才能求解.
3.能的轉化與能量守恒的應用
如圖4所示,質量是m的劈A與質量m的物體B位于靜止的光滑水平面,物體B的左端用輕質彈簧進行固定,一個質量是m的小球C從劈光滑的弧面上距離水平面的高度是h的地方從靜止下滑,求運動中彈簧的最大彈性勢能.

圖4

本題的解題難度通常不大,學生只要充分掌握了動量守恒以及機械能守恒兩大定律,就能輕松解決該問題.因此,在對能量轉化與能量守恒相關問題進行處理時,需注重整體思想,也可運用隔離法,從而使學生實現高效解題.
綜上所述,高中物理具體解題中運用整體法與隔離法時,首先需依據題目選擇合適的方法,通常是外力選擇整體,而內力選擇隔離,在對物理其他的知識學習時,也需學會整體與隔離的配合,這不僅可以使學生更好的理解物理力與運動之間關系的掌握,而且還能使學生自身的思維能力得到有效提升.

