基于Quanser平臺的旋轉單級倒立擺控制系統的研究與實現

戴 彥，呂宏麗

(唐山學院a.河北省智能數據信息處理與控制重點實驗室；b.唐山市智能運動控制系統重點實驗室，河北 唐山 063000)

0 引言

在控制系統傳統設計中，多通過純數字仿真的方式對系統進行分析，而純數字仿真大都以近似的數學模型為基礎，往往由于對一些參數的忽略而得不到理想的控制效果，甚至會出現仿真的結果與實際應用的效果相差很大的情況[1-2]。為解決該問題，可以考慮把實際系統放置在仿真系統中進行研究，此過程稱為半實物仿真[3-5]。加拿大Quanser公司開發的Quanser平臺即可以把控制對象引入仿真系統中，通過Quanser的實時內核實現控制器參數的在線調整。倒立擺系統是典型的高階次、多變量、強耦合的非線性系統。對倒立擺系統的仿真研究能有效反映許多關鍵問題，如非線性、魯棒性、跟蹤問題等。因此，本文基于Quanser平臺，在Matlab/Simulink中搭建旋轉單級倒立擺的實時仿真與控制平臺。

1 旋轉單級倒立擺系統動力學模型

旋轉單級倒立擺系統模型如圖1所示。旋轉臂轉軸連接于直流伺服電機SRV02系統上，且可被其驅動。該臂長度為Lr，轉動慣量為Jr。當旋轉臂逆時針旋轉時，旋轉臂旋轉角θ增大。當直流電機電壓為正時，旋轉臂轉向逆時針方向。擺桿與旋轉臂的末端相連，長度為Lp，質心在Lp/2處，質心的轉動慣量為Jp。當擺桿完全處于直立即在垂直位置時，其擺桿角度α為0；當它轉向逆時針方向時，則擺桿角度α增大。

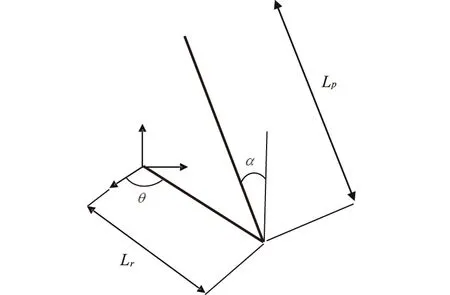
圖1 旋轉單級倒立擺系統模型

由圖1可知，旋轉單級倒立擺系統的動能可由四部分組成：旋轉臂在水平面內的轉動動能、擺桿在豎直平面內的轉動動能、擺桿質心在水平面內的移動動能、擺桿質心在豎直平面的移動動能。旋轉臂所在的水平面為零勢能面，則系統的勢能即為擺桿的重力勢能[6-8]。

運用拉格朗日方程建立倒立擺系統的動力學模型[9]。設整個系統的動能為T，勢能為V，模型如式(1)、式(2)所示。

(1)

(2)

式中，Jr為旋轉臂的慣性力矩(kg·m2)，Jp為擺桿的慣性力矩(kg·m2)，mp為擺桿的質量(kg)，Lr為旋轉臂的長度(m)，Lp為擺桿的長度(m)，θ為旋轉臂的角度(°)，α為擺桿的角度(°)，g為重力加速度(m·s-2)。

動能與勢能差設為L，則

(3)

得到旋轉單級倒立擺的拉格朗日方程式(4)，

(4)

式中，t為時間(s)，τ為旋轉臂扭矩(N·m)，Br為旋轉臂的粘滯摩擦力矩或粘性阻尼(N·m·s/rad)，Bp為擺桿的粘滯摩擦力矩或粘性阻尼(N·m·s/rad)。

對式(4)進行線性化處理，得到線性方程組如式(5)所示。

(5)

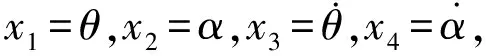
(6)

式中，A為

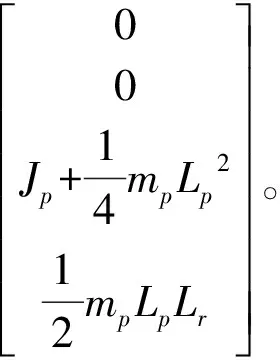
(7)

2 控制器設計

本文采用PID控制器對旋轉單級倒立擺進行控制，其仿真框圖如圖2所示。PID算法的控制規律如式(8)所示。

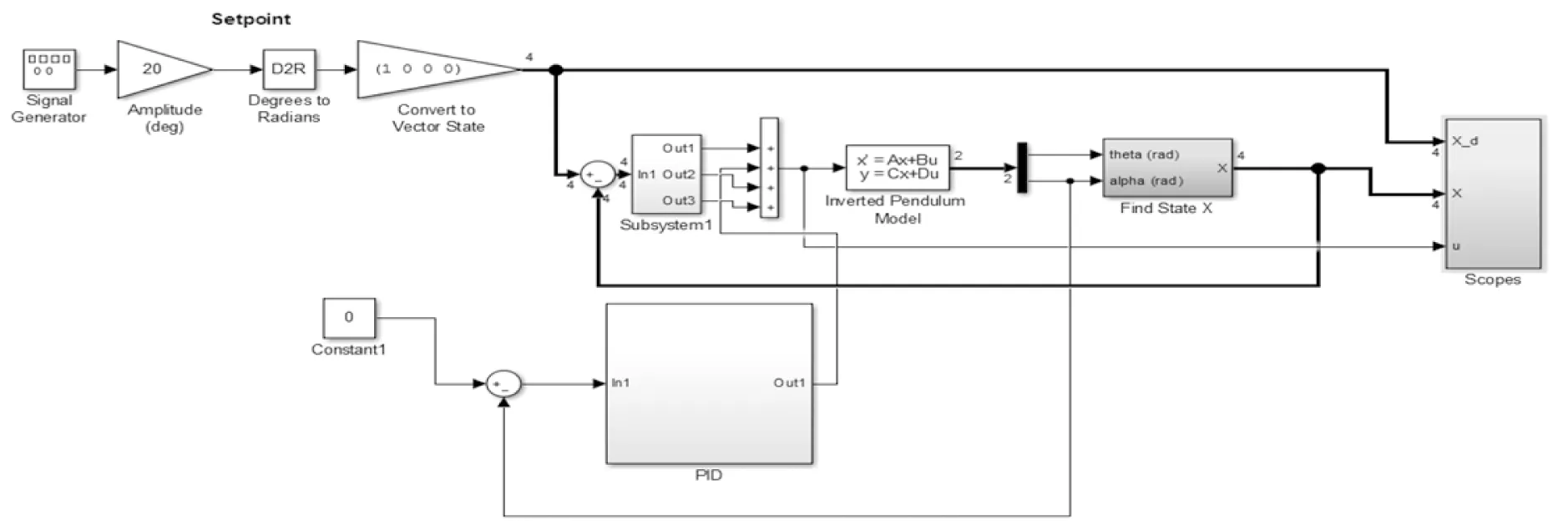
圖2 旋轉單級倒立擺控制系統仿真框圖

(8)

式中，kp表示比例系數，顯示誤差信號的瞬時值大小，能改變系統響應的快速性；ki表示積分時間常數，顯示誤差信號的累加值，能改變系統響應的準確性；kd表示微分時間常數，顯示誤差信號的變化趨勢，能改變系統響應的平穩性。

3 旋轉單級倒立擺控制系統

3.1 硬件介紹

旋轉單級倒立擺控制系統裝置如圖3所示。在此裝置中，在水平面上剛性旋轉臂的一端用一個旋轉伺服電機來驅動，另外一端安裝一個一自由度的轉軸。在此轉軸上安裝擺桿，電機通過控制旋轉臂的轉動可使擺桿穩定于垂直倒立的狀態。

圖3 旋轉單級倒立擺控制系統裝置

3.2 對旋轉單級倒立擺控制系統的實時控制

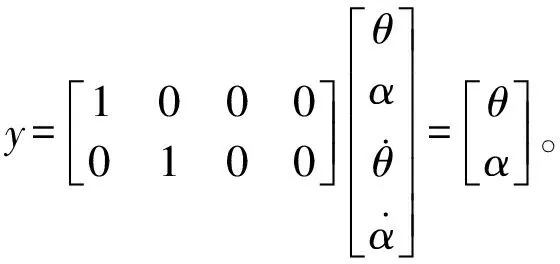
圖4為旋轉單級倒立擺控制系統實時控制Simulink框圖。Swing-up模塊為起擺模塊；Enable Balance Control模塊為角度比較模塊，擺桿角度期望值為12°，當角度小于12°時啟動PID控制模塊，大于12°時開關不變繼續執行起擺模塊。SRV02-ET+ROTPEN-E為直流伺服電機和倒立擺模塊構成的旋轉單級倒立擺控制系統硬件采集模塊。

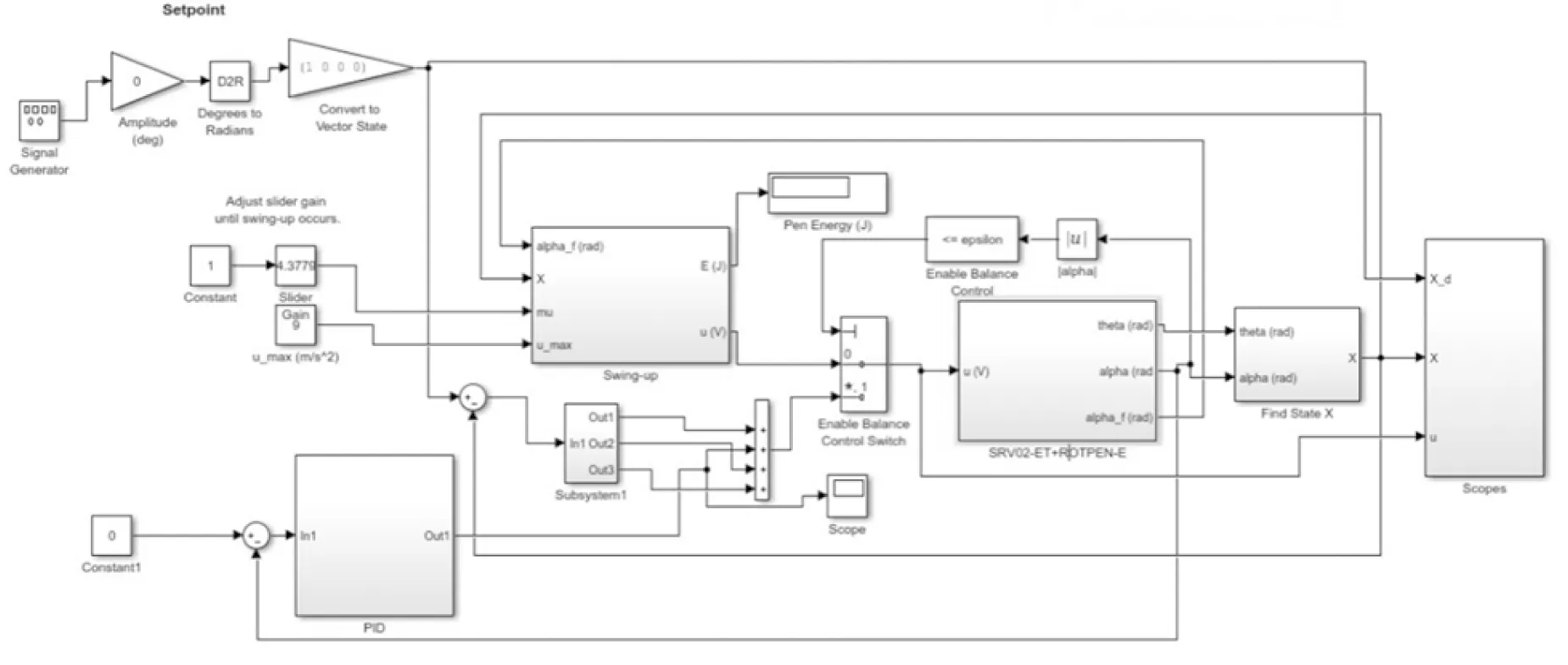
圖4 旋轉單級倒立擺控制系統實時控制Simulink框圖

旋轉單級倒立擺控制系統的硬件設備通過數據采集卡將計算機與受控對象相連，構成閉環控制結構[10]。Quanser軟件兼容Matlab軟件，在Windows環境中能夠啟動由Matlab/Simulink模型生成的硬件可識別代碼，通過USB接口由數據采集卡向受控對象發送或收集數據，達到實時控制的目的。

3.3 旋轉單級倒立擺控制系統實時控制仿真

調試程序時，采用湊試法確定PID調節參數：對參數進行先比例、后積分、再微分的整定步驟。首先進行比例整定：將比例系數由小調大，并觀察相應的系統響應，直至得到反應快、超調小的響應。僅調節比例系數，系統將會產生極大的靜差。其次進行積分整定：先設為一個比較小的數，慢慢增大，觀察系統的響應變化，使系統不僅能夠實現其所要的功能，而且還能夠消除靜差。根據系統的響應情況不斷修改比例系數和積分系數，直至可以實現系統要求的功能。最后進行微分整定：將微分系數從零遞增，以改善動態過程。最終確定控制參數為kp=11，ki=0.2，kd=0.2，倒立擺控制可達到要求。旋轉單級倒立擺控制系統實時控制仿真如圖5所示。由圖5可知，倒立擺控制系統調節時間為7s，其中α，θ，u響應平滑，抖動小。

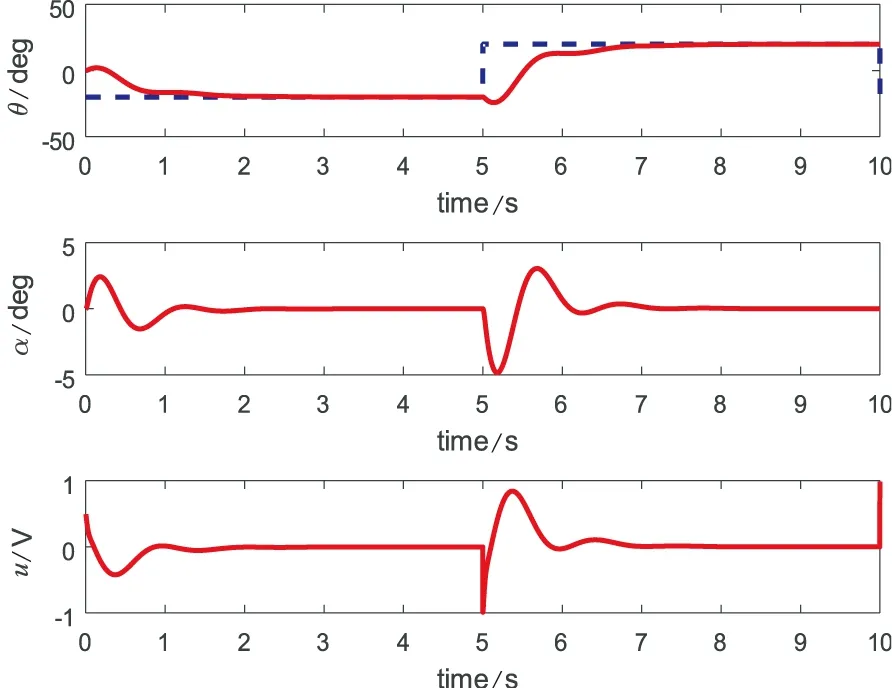
圖5 旋轉單級倒立擺控制系統實時控制仿真圖

4 結論

本文基于Quanser平臺搭建了旋轉單級倒立擺實時控制系統，建立了旋轉單級倒立擺系統動力學模型，分析了系統的穩定性。面向實物受控對象設計了PID控制器，由仿真圖和實物控制效果可知，控制器實時控制效果較好。同時，在該控制系統平臺上，可以開發控制算法，實時修改控制器參數。通過人機界面，可以直觀地比較不同控制算法的優劣，為控制算法的研究提供依據。