發動機連桿熱-結構耦合性能分析及優化

李曉婧，張穎博，高 欣

(1.唐山學院a.交通與車輛工程系；b.河北省智能裝備數字化設計及過程仿真重點實驗室，河北 唐山 063000；2.阜新德爾汽車部件股份有限公司，遼寧 阜新 123000)

0 引言

連桿作為發動機重要的組成部件，其作用是連接活塞和曲軸并將活塞的往復運動轉化為曲軸的旋轉運動而對外輸出動力[1-2]。為此，連桿的運動既包含平動又包含轉動，其受到載荷的大小和方向均是變化的，這導致了連桿的破壞形式以疲勞斷裂為主[3-5]。目前，對連桿的研究主要集中于在單純力載荷下的疲勞壽命分析和結構優化[6-9]，但是在實際的工作中連桿往往受到較高的溫度載荷，在溫度載荷作用下連桿的應力和應變均與單純力載荷下的應力和應變存在較大的差異。因此，本文主要對某型連桿在熱-結構耦合作用下的應力分布和疲勞壽命進行分析，并以分析的結果為依據對連桿進行結構優化，以改善其性能。

1 連桿機構的運動學分析

發動機的連桿機構如圖1所示。

圖1 連桿機構

圖1中，在活塞的上極限位置建立坐標系，曲柄與水平基線的夾角為α，連桿與水平基線的夾角為β，活塞中心B與B1點的距離為x，根據連桿機構的位置關系可求得x為：

x=OB1-OB=l+r-(rcosα+lcosβ)，

(1)

式中，r為曲柄的半徑，33.65mm；l為連桿的有效長度，139.65 mm。

根據△OAB可得協調方程：

lsinβ=rsinα。

(2)

三角函數的恒等式：

sin2β+cos2β=1。

(3)

將式(2)和式(3)帶入式(1)可得：

(4)

式中，λ為曲柄半徑與連桿長度比，λ=r/l；ω為曲柄的角速度，ω=2πn/60，n=5 000 r/min。

對式(4)關于時間求二階導數，求得活塞的加速度為：

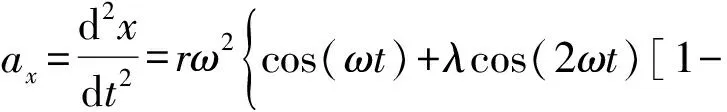
(5)

根據式(5)繪制加速度曲線，如圖2所示。

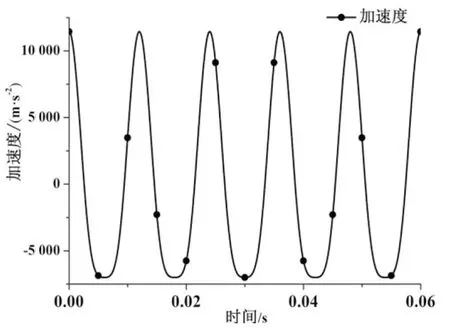
圖2 加速度曲線

2 連桿機構的受力分析

連桿的質心示意圖如圖3所示。

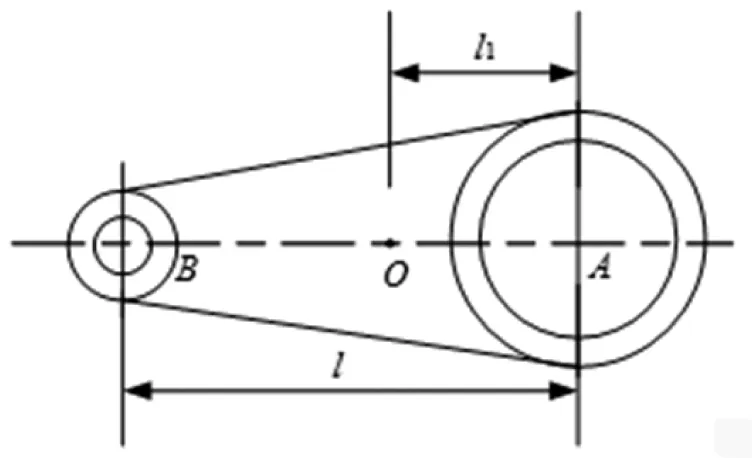
圖3 連桿的質心示意圖

曲柄連桿機構工作時，連桿會受到氣體燃燒時作用到活塞的壓力和系統的慣性力。連桿在工作平面做平動和旋轉的復合運動。為了簡化分析，采用質量代換法將連桿質量轉化為平動質量和旋轉運動質量，則連桿的平動質量計算公式為式(6)；連桿的旋轉運動質量計算公式為式(7)。

m1=mh+ml(l-l1)/l，

(6)

m2=mq+mll1/l，

(7)

式中，m1，m2分別為平動質量和旋轉運動質量；mh為活塞的等效質量，0.34 kg；mq為曲柄的等效質量，5.68 kg；ml為連桿的等效質量，0.68 kg；l1為連桿大頭圓心距質心的距離，34.03 mm；l為連桿小頭圓心距連桿大頭圓心的距離，76.47 mm。

系統的慣性力主要包括兩部分：一是平動慣性力F1；二是旋轉慣性力F2。結合式(5)可求得兩個慣性力分別為：

F1=-m1ax。

(8)

F2=m2rω2。

(9)

活塞受到的燃氣壓力Fp為：

(10)

式中，D為活塞直徑，78 mm；ΔP為缸體內氣體壓力差，7.95 MPa。

3 連桿的熱-結構耦合分析

3.1 連桿的三維模型

連桿的三維模型采用Creo2.0繪制，并導入Workbench中。連桿模型是裝配體，結構比較復雜。為了減少分析時間，同時為了研究連桿強度，在保證計算準確的情況下，采用布爾運算將連桿的端蓋和連桿合并成一個整體，處理后連桿的三維模型如圖4所示。

圖4 連桿的三維模型

3.2 材料屬性及網格劃分

連桿的材料為40Cr，其材料性能參數為：密度7 870 kg/m3；彈性模量211 GPa；泊松比0.277；屈服強度785 MPa[7]；材料在95%存活率下的疲勞壽命滿足lgN=19.68-5.837 lgσ，其中N的單位為103次，應力的單位為MPa；比熱容553 J/(kg·K)；熱導率44 W/(m·K)；線膨脹系數1.279×10-5/K[10]。

對模型進行四面體網格劃分，為了保證計算結果的精度，對連桿大頭、小頭的過渡處做網格細化，結果如圖5所示，模型共有157 828個節點，103 314個單元。

圖5 連桿的網格模型

3.3 載荷的確定

連桿正常工作時會受到系統的慣性力和活塞的燃氣壓力，同時由于燃氣燃燒的影響還會受到熱載荷。四沖程發動機在一個工作循環(兩次圓周運動)中，缸體內有一次氣體燃燒，但發動機的轉速較高，這次燃燒和下次燃燒間隔的時間非常短，所以可認定連桿受到的是一個大小恒定的溫度載荷。根據參考文獻[7]可知溫度載荷為700 ℃，因此，在連桿小頭的外表面施加700 ℃的熱輻射載荷，同時在連桿的所有外表面添加空氣對流載荷。

經分析可知，當發動機位于對外做功沖程起點時，連桿受最大的壓縮力；當發動機位于吸氣沖程起點時，連桿受最大的拉伸力。本文分析這兩種工況的熱-結構應力狀態。連桿工作時實際是“二力桿”，當連桿處于最大壓縮狀態時，連桿小頭的載荷為爆燃壓力減去活塞組件的慣性力，連桿大頭的受力為連桿小頭受力減去連桿的慣性力；當連桿處于最大拉伸狀態時，連桿小頭的載荷為活塞組件的慣性力，連桿大頭的受力為連桿小頭受力減去連桿的慣性力。

熱-結構耦合分析模型采用如下方法建立：首先在Workbench軟件工作頁面添加Transient Thermal熱分析模塊，然后在熱分析選項的Solution選項中建立結構分析模塊，熱-結構耦合分析模型的關聯關系如圖6所示。分別在熱分析模塊和結構分析模塊施加上述載荷。

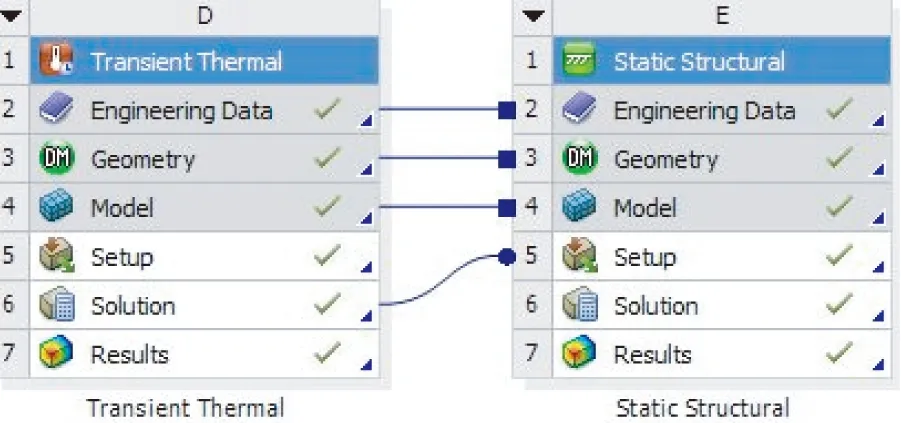
圖6 熱-結構耦合分析模型

3.4 結果與分析

連桿的溫度分析結果如圖7所示。根據圖7可知，連桿小頭的最高溫度為673.33 ℃，從連桿小頭到大頭溫度呈逐漸下降趨勢，至連桿大頭溫度衰減為339.45 ℃。

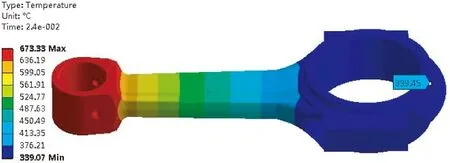
圖7 連桿的溫度

對連桿進行熱-結構耦合分析，在受壓和受拉兩種工況下的應力云圖如圖8所示。連桿受拉時最大應力為172.02 MPa，連桿受壓時最大應力為496.16 MPa。兩種工況下連桿最大應力出現的位置相同，均在連桿小頭與連桿柄連接處。同時連桿柄與連桿大頭連接處以及連桿小頭的內圓面也存在比較大的應力。根據以上分析可知，連桿應力均小于屈服強度。

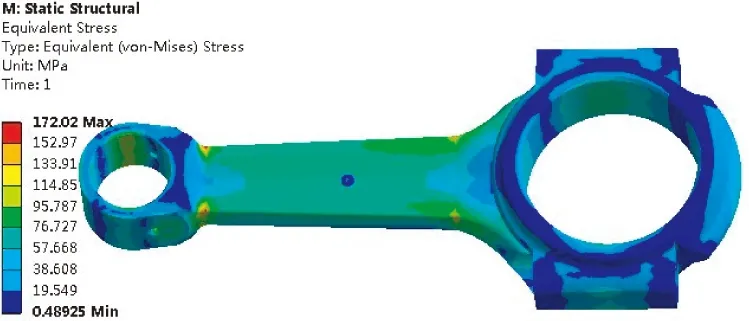
(a)受拉

(b)受壓圖8 連桿的應力云圖

由熱-結構耦合分析結果可知，因承受最大應力，連桿小頭與連桿柄連接處的截面為危險截面。此處在受拉和受壓時應力方向相反，其應力分別為-172.02 MPa和496.16 MPa，則應力循環特性系數R=-172.02/496.16=-0.346 703，應力幅值為334.09 MPa，材料的綜合疲勞影響系數為0.79。利用軟件中Fatigue Tool模塊分析連桿的疲勞壽命，采用“Good man”理論進行計算，計算結果如圖9所示。由圖9可知，連桿小頭與連桿柄連接處最小疲勞壽命為1.527 9×105次，且連桿柄的疲勞壽命從兩端過渡處向中間遞減。

圖9 連桿的疲勞壽命

4 連桿的優化設計及性能分析

4.1 連桿的優化設計

根據上文的分析可知，連桿小頭與連桿柄連接處的截面為危險截面，其原因是圓角過小出現了應力集中的現象，因此可以適當地增加圓角以降低應力集中，同時該位置圓角過大易與缸體發生干涉，所以對此處的結構進行優化設計：增加此處截面的過渡圓角為1 mm，連桿中心上下兩側的厚度分別增加0.5 mm(如圖10所示)，該截面其他輪廓尺寸不變，且連桿大頭過渡處的輪廓尺寸保持不變。然后采用Creo2.0中“掃描混合”命令重新建立連桿柄模型。

圖10 連桿的優化設計

4.2 優化后連桿的性能分析

對優化后連桿的網格劃分及施加的熱載荷和力載荷與原型分析時一致。由于連桿的改動較小，其溫度變化較小，與原型連桿的溫度幾乎一致，因此不再對溫度分布結果進行討論。

對優化后的連桿進行熱-結構耦合分析，在受壓和受拉兩種工況下的應力云圖如圖11所示。連桿受拉時最大應力為140.96 MPa，連桿受壓時最大應力為406.54 MPa。兩種工況下優化后連桿最大應力出現的位置相同，且與優化前的位置一致。優化后的連桿在受拉和受壓工況下的最大應力與原型相比分別減小了18.05%和18.06%，且連桿柄的應力與優化前相比也顯著減小(圖中藍色區域增大)。

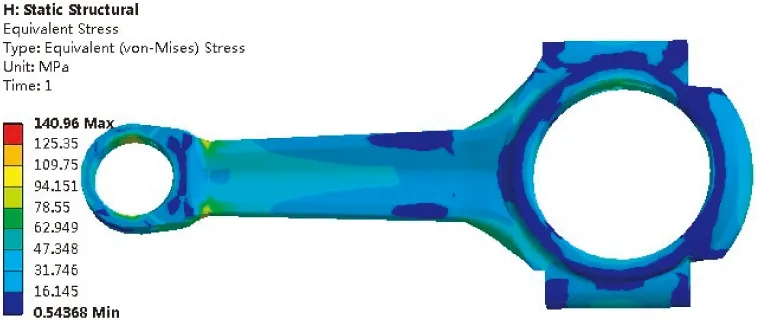
(a)受拉

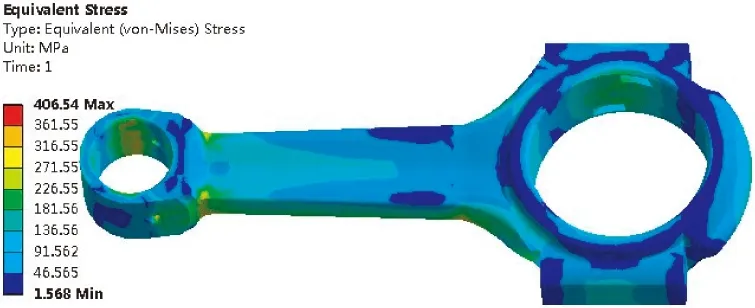
(b)受壓圖11 優化后連桿的應力云圖

利用熱-結構耦合分析結果對優化后連桿的疲勞壽命進行分析。根據兩種工況下的最大應力可知，連桿小頭與連桿柄連接處應力循環特性系數R=-140.96/406.54=-0.346 731，應力幅值為273.75 MPa，材料的綜合疲勞影響系數不變，分析理論與原型分析時相同，分析結果如圖12所示。由圖12可知，優化后連桿的疲勞壽命分布形式基本保持不變，但其最小疲勞壽命已為3.003 9×105次，比原型連桿的疲勞壽命提高了96.60%。

圖12 優化后連桿的疲勞壽命

5 結論

(1)采用有限元仿真法建立了連桿的熱-結構耦合分析模型，分析了連桿在熱載荷和力載荷耦合作用下的應力分布和疲勞壽命，該方法可以用于連桿結構的設計及優化。

(2)對原型連桿進行了優化改進，優化后連桿的應力顯著減小，但其疲勞壽命增加了96.60%，很好地改善了連桿的性能。