基于“工學一體化”的傅里葉級數教學設計探討

嚴 明

（福州職業技術學院，福建福州，350108）

一、引言

“信號與系統”是我國電子信息大類相關專業都需開設的一門專業基礎課，目前國內主流的教材[1-3]對該課程撰寫的思路都十分清晰，即由求解微分方程的方法引入，由淺入深地將傅里葉級數（變換）、拉普拉斯變換、Z 變換等知識環環相扣，串成一條主線。然而，傅里葉級數作為時域跨入頻域的第一道門檻，因理論公式繁多，讓部分學生望而卻步，于是出現了死記公式的現象，并對公式感到迷茫且無從下手。為提高學生對傅里葉級數知識的吸收效果，國內本科院校教師進行了一系列教學研究。國防科技大學曹聚亮等[4]提出指數信號的三層次法，通過數學層面、圖形層面、應用層面等，盡可能使學生較好地理解時域頻域分析過程；西北師范大學唐榮安等[5]建議在教學中從物理詮釋方面對傅里葉變換性質進行講解；王靜等[6]從學生認知調查和原因分析入手，在教學設計中設置懸念引出傅里葉級數主題，通過簡單、典型的舉例進行教學，并進行課后反饋。有的本科院校教師則利用Matlab GUI界面查看傅里葉級數展開項等方式，使學生從直觀上理解傅里葉變換。[7-9]而高職高專院校目前在這一方面尚未有探討。

本文根據高職學生實際情況，提倡“教為主導，學為主體”的教學思想，學生通過動手實踐，自主疊加展開項來驗證波形，同時利用Matlab 仿真查看三維空間圖，從而對傅里葉級數的認識從“客觀存在”提升到能“加以分析”的程度。

二、傅里葉級數的教學總體設計

（一）“工學一體化”教學模式簡介

工學一體化教學模式從理實一體化發展而來。[10]在傳統理論教學中，教師以灌輸知識為主，學生被動接受，這勢必導致學習積極性的磨滅。著名的職業教育專家趙志群教授中指出，教學要逐漸轉變為以學生為中心。為了突出課堂以學生為中心，工學一體化教學以項目或任務為驅動，在確定項目（任務）的主題后，分析為完成該任務需要在任務實施前準備什么；在任務實施過程中做什么、學什么；在任務實施完成后如何進行相應的評價。該教學思路強調學生在實施任務過程中掌握新知識和技能，比較適合高職教育的工科課堂教學。[11]

（二）教學過程結構表設計

為使教學思路更清晰，傅里葉級數教學從單頻正弦信號引入，到任務實施與驗證，再到師生互動分析等過程，均需進行詳細的教學過程設計。現借助工學一體化教學模式，用表格展現任務實施過程中教師和學生需完成的事項和對應的知識點、評價標準等（如表1）。

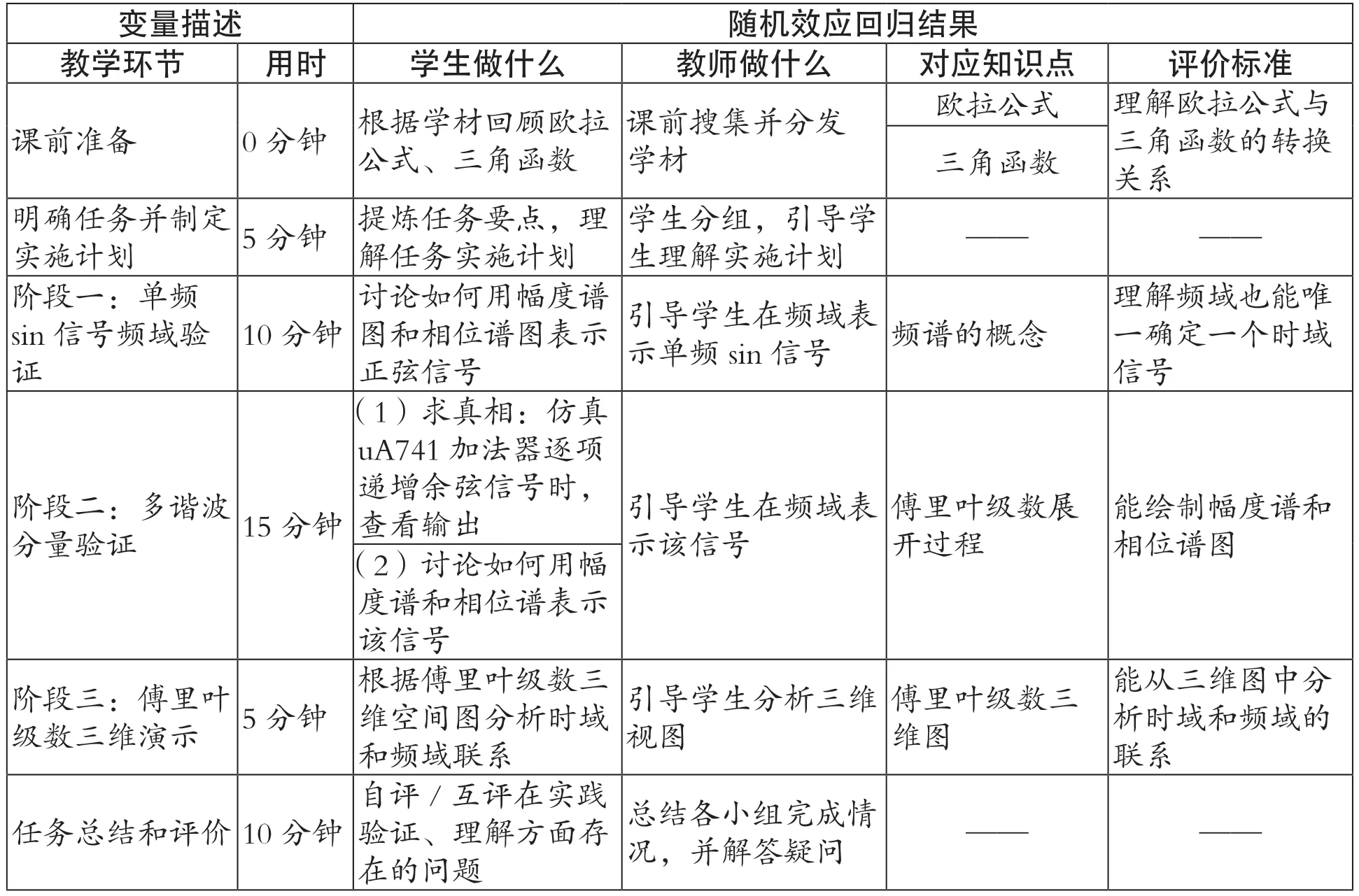
表1 教學過程表格化設計

三、傅里葉級數教學過程詳細設計

（一）課前準備

歐拉公式及三角函數是傅里葉級數兩種表示形式間的轉換橋梁，因此需要學生課前做好一定的準備工作。教師在課前需提供指數與三角函數如何建立聯系的學材：任意一個復數A可在復平面上找到對應的一個點（如圖1），當加入單位圓概念后，A 點坐標不僅可以表示為A=a+jb，也可以表示為z=r(cosθ+jsinθ)，教師由此根據極坐標表示方式，引出歐拉公式e^jθ=cosθ+jsinθ，這就在復平面上建立起指數與三角函數間的聯系。

令θ=ωt，其中ω 為角頻率，則歐拉公式變為：e^jωt=cosωt+jsinωt，隨著時間t的推移，歐拉公式等號左邊可看作是繞著圓周逆時針不停旋轉的點A（如圖1），等號右邊是A 點繞圓周運動時在時間軸上的投影，即可理解為歐拉公式是A 點的兩種表示方式。由于A 點在時間軸t 上的推移，慢慢拉出一條螺旋線，其x 軸投影為cosωt，其y 軸投影為sinωt（如圖2）。

圖1 復平面上的點

（二）明確任務并制定實施計劃

明確本教學任務為：驗證傅里葉級數展開式，并理解頻譜概念。考慮到任何周期信號的傅里葉級數展開項均由正余弦函數線性疊加而成，學生若能獨立分析單一的、或某幾個正余弦函數疊加，就可理解無限個線性求和的結果。因此在實施教學時，首先思考單頻正弦信號在頻率軸上如何表示（即幅度譜和相位譜）。反過來，已知頻譜圖，求時域的正弦信號表達式，進而得到結論：頻域和時域均可唯一表示一個信號（即同一信號的兩種表示方法）；更進一步，當展開項（諧波分量）逐漸增多時，驗證其趨于某個（矩形）波形；當展開項個數趨于無限個，即為傅里葉級數展開式。

根據以上實施思路，本單元教學場所需為模擬電子技術實訓室，或者機房（電腦均已安裝Proteus 軟件，且可播放音頻），本文的教學環境以機房教學為例。

階段一：從單頻正弦波引入頻譜概念

已知正弦信號如下：

其中f=50Hz，或ω=2πf，初始相位為π/4（如圖3）。為了使學生更快建立起頻譜概念，將該波形的橫軸由時間t 轉為頻率后，用幅度譜、相位譜圖表示單頻正弦信號。反過來，根據幅度譜、相位譜寫出時域的正弦信號表達式（注意圖3 相位譜中初始角是π/4=0.7854，因此相位譜高度接近0.8）；最后引導學生理解：在頻域也能唯一確定正弦信號，頻域是信號的另一種表示方式。于是得出結論：我們習慣思維在時域表示一個信號，其實在頻域也可表示一個信號，而且時域和頻域表示同一個信號的效果是完全相同的。

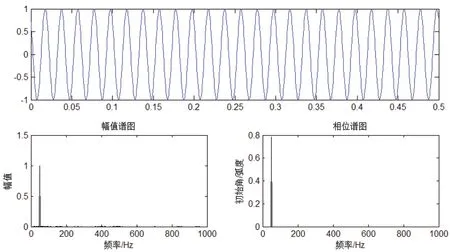
圖3 正弦信號的時域和頻域表示（Matlab 單邊譜）

階段二：傅里葉級數展開項驗證

為了驗證矩形波傅里葉級數是無限多個余弦信號疊加而成，可根據傅里葉級數系數公式，引導學生求解前10 個展開項，學生根據展開項設置Proteus 元器件參數，并在設計的加法器電路（如圖4）左邊逐項遞增地接入展開項的余弦波，通過示波器觀察波形變化。電路輸出端接喇叭，可對比不同展開項疊加波形后的音頻。即通過動手求解系數、眼睛觀察波形、耳朵辨別音頻等方式加深對傅里葉級數展開項的理解。

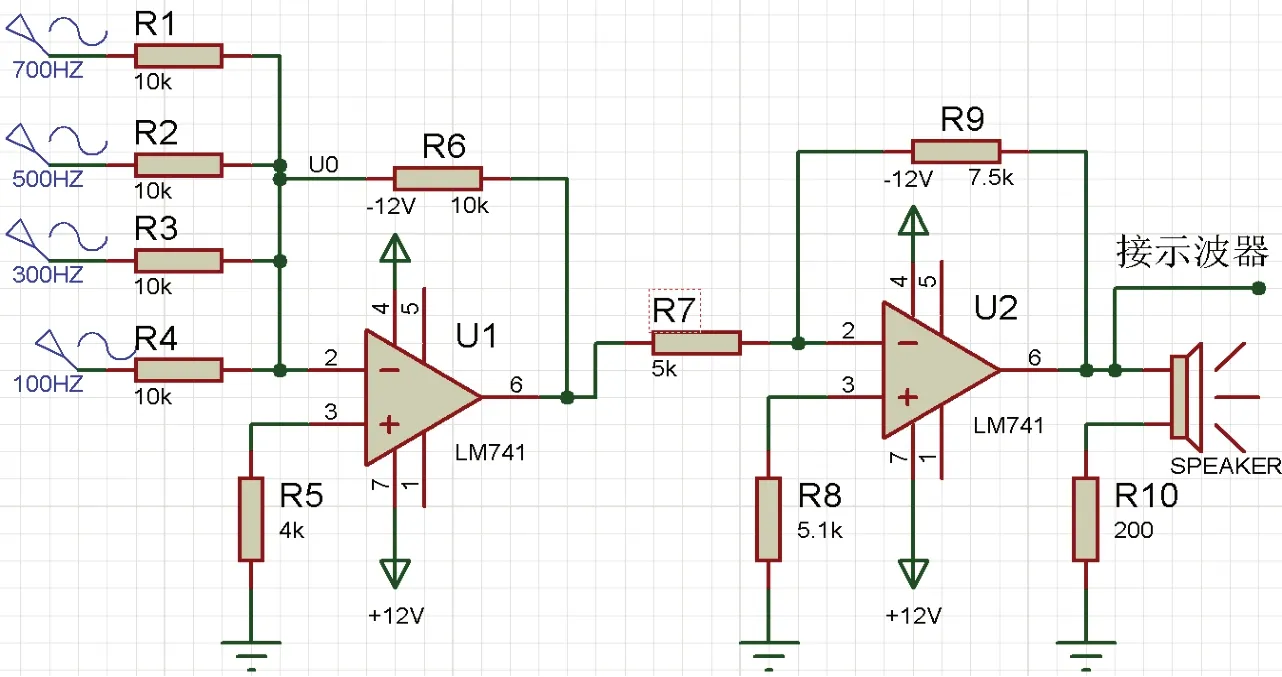
圖4 多個正余弦信號相加放大的電路圖（Proteus）

通過本階段任務，得到結論：隨著諧波分量逐漸增多，疊加的波形越來越接近矩形波（如圖5）。當在時域波形越來越接近矩形波時，對應的頻域圖則按順序增加對應的譜線（如圖6）。也即時域每增加一個諧波分量，頻域中就增加一條對應頻率的譜線，由此也可說明頻域和時域在表示一個信號的形成過程是完全相當的。隨著諧波分量無限疊加，波形就趨近于矩形，也就得到傅里葉級數展開式。

圖5 諧波分量遞增的時域波形（Matlab）

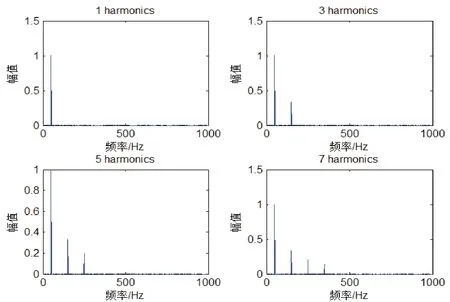
圖6 諧波分量遞增的頻譜波形（Matlab）

階段三：三維傅里葉級數分析

以上階段任務實施采用了Proteus、Matlab仿真實踐，分別通過驗證時域和頻域波形來引導學生理解傅里葉級數和頻譜的概念，本階段將時域和頻域的圖示結合在一張三維空間圖中，仍以矩形波的傅里葉級數展開為例。

由于矩形波既是偶函數，又是奇諧函數，因此其傅里葉展開只可能含有奇次諧波的余弦項。圖7 為了分析方便，只取前3 次諧波分量分析時域和頻域的統一性。從時間軸往右邊看，時域疊加波形是由1 次諧波和3 次諧波相加而成；從頻率軸往里看，1 次諧波對應頻率ω_1，3 次諧波對應頻率3ω_1，即兩個諧波疊加的波形在頻域中也可唯一確定。這將使學生進一步加深在時域和頻域中分析同一個信號的理解程度。然而時域的缺陷在于時域波形隨著諧波分量的增多，波形計算越來越復雜；而頻域分析卻十分簡單，即一個諧波分量增加一條譜線，因此在信號系統中分析頻域是十分有利的。

圖7 傅里葉級數的三維空間圖

四、教學評價

工學一體化教學中，應盡可能讓所有的學生都參與到評價過程中。[12]在本單元的傅里葉級數教學過程中，2 人為一組，以實踐過程評價為主，結果性評價為補充。評價的主體包含學生自評、互評和教師評價，除了評價學習態度、溝通協調方面，主要以階段性任務完成情況為評價單元，根據表1 右側的評價標準，細化具體行動。評價的目的主要是為學生提供本次課堂實踐過程中需要改善的方面，同時也幫助學生梳理知識架構。

五、結束語

本文針對學生在學習傅里葉級數章節時，因理論較多而迷茫問題，借助工學一體化教學中以學生為主體的思路，讓學生參與其中，教師引導解惑完成教學任務。通過在高職課堂實踐，學生在課堂上不再木然，個別學生甚至在課堂上獨立完成三角波的疊加演示圖，表明該教學思路提高了學生學習的積極性，而且對提升傅里葉級數教學效果具有一定實際意義。