模塊化生產模式下的服裝產品組合優化決策
韓曙光, 顏偉雄, 胡覺亮
(1. 浙江理工大學 理學院, 浙江 杭州 310018; 2. 浙江理工大學 服裝學院, 浙江 杭州 310018)
服裝產品組合決策是服裝零售商的重要經營問題。零售商需要提供多款式的服裝來滿足消費者的個性化需求。在消費者需求越來越多元化的今天,對服裝部件元素、款式和版型進行多樣化的模塊化組合生產,可以快速滿足消費者的需求[1]。然而,如何選擇由供應商提供的多款式服裝是一個非常具有挑戰性的問題,因為這需要權衡消費者的選擇偏好和零售商可能的盈利情況等。零售商要獲得利潤最大化的服裝產品組合,最簡單的方法就是窮舉所有可能的服裝組合,然后選擇利潤最大的組合;然而同一款風格的服裝,往往具有多種垂直差異化產品[2],不可能對其一一羅列,這樣很難通過窮舉確定最優的產品組合。
近年來,模塊化的思維設計方法開始運用到服裝上,將服裝部位進行模塊劃分,在部位模塊上增添或刪減元素,設計出具有多樣性和新穎性的服裝產品族[1,3];此外,在服裝工藝生產中,有學者提出將服裝工序進行模塊劃分,并運用于服裝智能傳輸系統,可有效改善現有服裝流水生產[4-5]。現已有企業在服裝個性化定制方面應用模塊化生產:辛巴達作為一家專注于服裝生產的柔性供應鏈平臺,劃分有打板、裁剪、縫紉、面料多個模塊工廠,運用互聯網技術對傳統工廠進行模塊化改造,取得了一些進展[6];國外李維斯推出Future Finish線上服務,采用模塊化設計技術理念,對牛仔褲進行自主模塊設計,實現牛仔褲數字化開發與生產[7]。因此,市場上產生了越來越多垂直差異化的多款式服裝產品,單一產品的經營策略是不可取的,提供多屬性且不同質量水平的產品策略才是最優的[8-9]。零售商需要根據消費者類型、產品價格、產品質量、產品的搜索成本以及產品規格大小等因素[10-12]對產品進行正確的組合決策。
本文主要討論模塊化服裝的產品組合優化問題。在模塊化生產模式下,生產垂直差異化服裝,分析模塊化服裝時尚度對消費者在服裝選擇性上的影響,討論為獲得利潤最大化,零售商對多款服裝進行產品組合決策;本文還研究了在多款式的服裝市場環境下,寡頭供應商與多個不同產品組合決策的零售商進行最優的利潤分配等。
1 問題描述與符號說明
傳統服裝生產是以服裝成衣為單位,按直線型流水作業,依次傳遞生產;而模塊化生產,則是結合服裝工藝和服裝結構劃分進行作業調整,擺脫傳統的設計生產模式束縛,將服裝部件模塊化分割,組合出造型元素時尚度不同和款式多樣化的服裝。
對于多款由模塊化組成不同時尚度的垂直差異化服裝,零售商需要根據市場消費者偏好對服裝產品進行組合決策。本文考慮在需求確定下,構建基于效用最大化的消費者選擇模型,設計關于垂直差異化服裝產品之間的有向圖,以最短路徑求得零售商最大利潤的產品組合。此外,進一步考慮,多零售商在不同貨架空間產生不同產品組合決策的情況下,供應商根據市場情況,通過最大流問題對多零售商進行合理的利潤分配。
符號說明如表1所示,對服裝產品組合有以下假設:1)不考慮銷售周期末產品殘值;2)不考慮補貨情況;3)每位消費者最多只購買單件產品;4)消費者心理估值服從均勻分布。

表1 參數定義Tab.1 Parameter definition
2 數學模型
本文將針對具有垂直差異的模塊化服裝產品構建服裝時尚度模型、消費者選擇模型和需求確定時零售商以及供應商決策模型。
2.1 模塊化服裝時尚度模型
服裝具有典型的季節性,其時尚度很大部分取決于服裝產品內包含的時尚元素:款式、花色圖案以及裝飾配件等[13-14]。假定服裝是由部件模塊和部件造型模塊組成[15],由于是垂直差異產品,其服裝風格固定,故服裝時尚度是在部件模塊的基礎時尚度上,對其他部位進行造型模塊的選擇,可以組成多款時尚度不同的服裝。
部件模塊可分為衣領、衣身、袖子、門襟、廓形等,而造型模塊是在部件模塊的基礎上進行多個屬性細分。由于服裝各部件的模塊都有其相應的服裝時尚元素,各屬性數值按該周期流行趨勢的時尚指數表示[13],由多個包含屬性的模塊向量組成矩陣[16],用0~1規劃整合求得時尚度。某部件i的屬性向量為Xi=(xi1,xi2,…,xij,…,xim)。yij=1表示選擇了時尚度為xij的部件造型;yij=0表示未選擇時尚度為xij的部件造型,則部件造型選擇向量為Yi=(yi1,yi2,…,yij,…,yim)。
服裝時尚度wj是由基礎款式的時尚度w0和各部件造型模塊的時尚度累加求和得到,其表達式為
(1)
故多款不同組合時尚度不同的服裝,其各款服裝的時尚度關系為:0≤w1≤w2≤…≤wj≤…≤wn。
2.2 消費者選擇模型
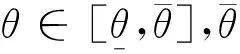
(2)
依據文獻[17],假設消費者估值分布函數為F(θ)=1-(1-θ)b,b>0,消費者根據效用最大來購買產品,由此得到的購買概率為
(3)
為保證αj≥0,即購買概率不小于零,需滿足式(2)。
2.3 單一零售商決策模型
假設產品需求確定,存在一個零售商,不考慮商品庫存、貨架空間且不存在競爭關系,根據到店消費者人數μ和購買概率αj,可確定產品j的需求量為Dj=μαj,則零售商利潤函數表示為
(4)
尋找垂直差異化產品的最優組合,即極大化利潤函數:
(5)
2.4 市場利潤分配模型
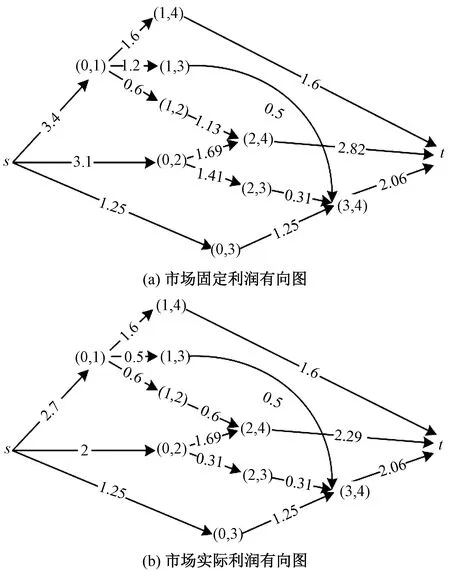
從市場利潤最大化的角度看,假設單寡頭的服裝供應商為零售商供貨,而服裝零售商在進貨中,由于服裝款式的多樣性,每個零售商固定的貨架空間η(η代表單位空間最大毛利潤)是不同的。零售商為獲得最大利潤,需要根據自身的固定空間,有選擇性地對服裝款式進行組合入貨,因此多零售商市場為獲得更多利潤,需要根據不同生產情況下的供應商為多個零售商進行合理供貨。
將構造以寡頭供應商為源點s,多個款式服裝作為節點和市場消費群t為終點的有向無環圖,通過最大流對市場t求最大利潤分配。如圖1所示,s為供應商,t為市場消費群,供應商s向市場消費群t輸出款式為A和B的服裝,其中s到t的1條路徑代表一零售商。圖中供應商到市場消費群有3條路徑,每一路徑表示為1種產品組合決策的零售商,故圖中表示有3種不同產品組合的零售商(s→A→t,s→A→B→t,s→B→t),對3個零售商進行利潤分配。該網絡中的最大利潤分配模型為
maxval(f)
(6)
f(vi,V)-f(V,vi)=0,vi∈M
(7)
f(s,V)-f(V,s)=val(f)
(8)
f(t,V)-f(V,t)=-val(f)
(9)
0≤fij≤ηij
(10)
式中:val(f)為服裝款式網絡流f的利潤,最大利潤分配為利潤值最大的網絡流;V={M,s,t},為網絡頂點的集合;s為源點;t為終點;M={v1,v2,…,vm},為網絡中除源點s和終點t之外的服裝款式集合;fij為款式{i}與款式集合{i,j}的實際利潤差;ηij為款式{i}與款式集合{i,j}的固定利潤差。
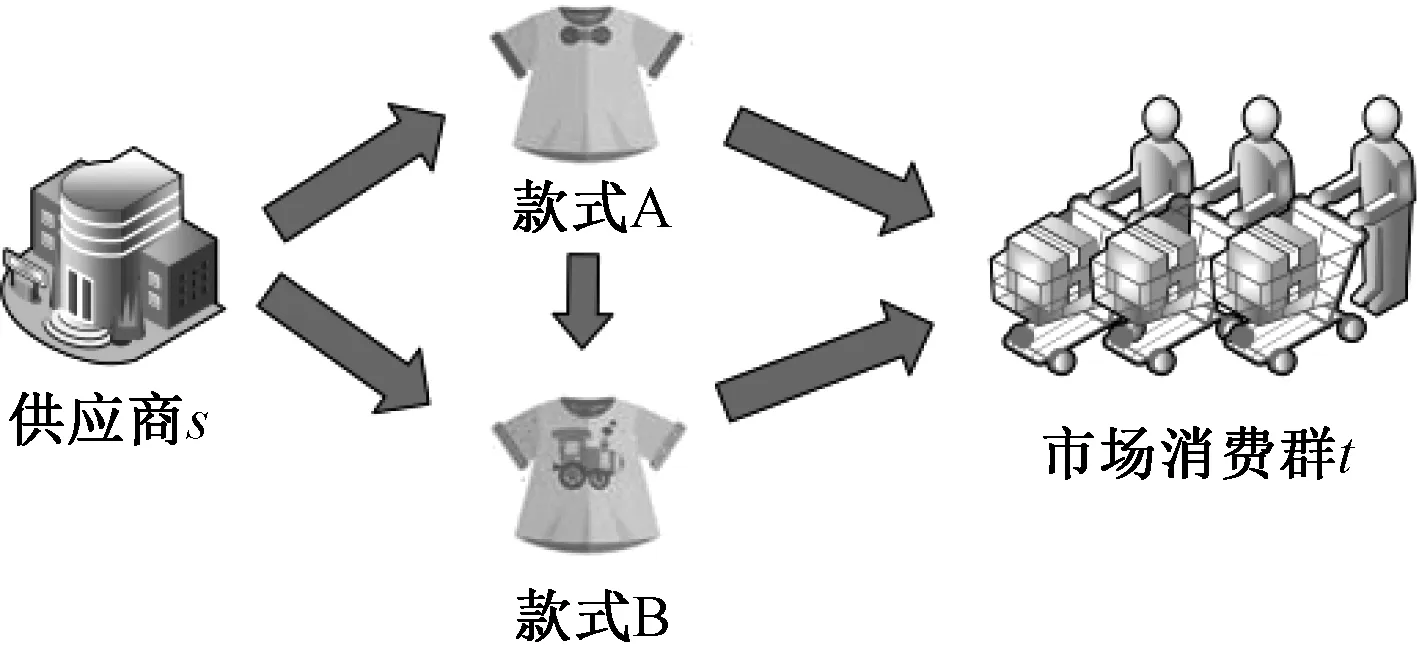
圖1 零售商選擇決策Fig.1 Retailer selection decision
式(7)~(9)為利潤流量的平衡約束。其中:式(7)表示中間節點的輸入利潤等于輸出利潤;式(8)、(9)分別表示源點和終點的輸入利潤流量等于其輸出利潤流量。式(10)為容量約束,即實際利潤不能超過固定利潤。
3 模型求解
3.1 最佳產品集合
通過滿足式(11)~(13)的條件優化多產品集合,并構建產品間的一個有向圖,通過最短路徑對式(5)進行零售商最大利潤求解并獲得最佳產品組合S*。
定理: 最佳組合S*產品集合滿足以下3個條件[18]:
(11)
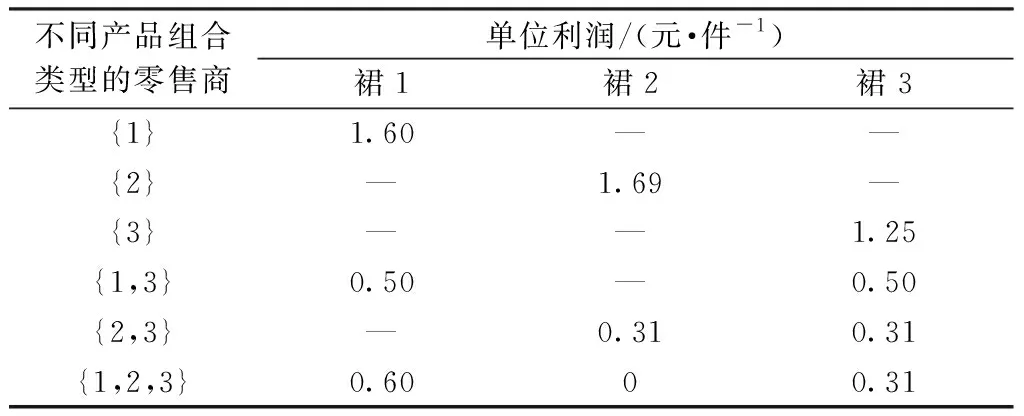
p1 (12) p1-c1≤p2-c2≤…≤pn-cn (13) 以上定理表明:在產品組合中,價格在時尚度水平上是嚴格遞增的,式(11)、(12)是最佳產品組合的必要條件;利潤在時尚度水平上是遞增的,說明在服裝周期內,根據服裝部件模塊的時尚元素選擇,時尚度越高,價格也將隨之遞增;式(13)說明時尚度越高的服裝,可獲得更高的收益。 步驟1:構造節點集,引入源節點(0,0)和目標節點(n+1,n+1)。 V4={(0,0),(n+1,n+1)} V=V1∪V2∪V3∪V4 步驟2:節點之間弧的距離為 (14) 在有向圖構造步驟中,n表示有向圖中共有n款服裝,引入0和n+1,分別表示產品集合的初始點和結束點,并不代表某一款式服裝。式(14)是節點(i,j)與(j,k)之間的距離,表示產品j利潤值的相反數。由于產品間的利潤大小為負,即從(0,0)到(n+1,n+1)的路徑值均為負,則得到的路徑值越小,產品組合利潤值越大,因此,可通過最短路徑求得利潤最大的服裝產品組合。 步驟1:構造節點集,引入源節點s和目標節點t: V4={s,t} V=V1∪V2∪V3∪V4 步驟2:節點之間弧的距離為 (15) 由于將有向圖的每個路徑看作一種產品組合類型的零售商,式(15)為零售商在自身的貨架空間下獲得的最大固定利潤。單一寡頭供應商根據服裝市場變化,從源點s為不同類型的零售商輸出服裝。供應商需要滿足自身的最大輸出,同時也要合理分配零售商的實際利潤。因此,根據供應商與各類型零售商之間構建的有向圖,將本問題轉化為供應商對各零售商的最大流利潤分配問題。 本文基于上文的求解方法,對模型進行求解分析,并討論服裝成本和其時尚度對零售商、供應商和整個供應鏈利潤的影響。 如果使用窮舉方法對3款裙子進行產品組合決策,則需要考慮7個分類:{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}。通過產品組合的優化設計,構造產品集,通過產品之間的利潤弧線連接起來,以有向無環圖(見圖2)表示各產品之間有效路徑的對應關系,圖中坐標(i,j)表示由一對產品(i,j)∈V組成,(0,0)和(4,4)為源點和終點,節點之間權重表示產品間帶負權值的單位利潤。通過帶負權值的最小路徑計算服裝零售商產品組合的最大利潤。 圖2 服裝產品集合有向圖Fig.2 Directed graph of apparel product set 圖2所示網絡包含5個有效路徑,路徑分類如表2所示。相比窮舉7種產品組合路徑,該組合優化的效果明顯,可排除2個無效組合。 表2 有效路徑與利潤Tab.2 Effective path and profit 由上述分析可知,將多款服裝進行有效組合,形成有效路徑,由于每個零售商的貨架空間產生單位利潤不同,因此不同的零售商根據其貨架空間進行最優產品組合決策,即每個零售商的最優產品決策各不相同。在時尚服裝市場中,往往會存在供不應求和供過于求的情況,為了盡可能滿足市場需求,在只有單一供應商下,供應商對多個不同產品組合類型的零售商進行合理的利潤分配,使市場的利潤最大化。 4.2.1 供不應求情形 圖3 供不應求情形下市場的利潤分配Fig.3 Profit distribution in market with short supply. (a)Directed graph of market fixed profit;(b)Directed graph of market actual profit 圖3(a)中弧的容量大小表示產品的單位固定利潤,即源點s向市場分配利潤為:裙1的單位固定利潤12.5元/件,裙2為18.27元/件,裙3為20.35元/件。源點s的單位固定利潤小于終點t,說明市場對該季度系列服裝需求過大,造成供不應求的狀態。圖3(b)中的弧表示產品實際的單位貨架利潤,供應商根據各貨架空間不同的零售商,按照市場需求利潤最大化,對零售商進行分配。求解得到市場最大單位利潤為51.12元/件,各類型零售商服裝組合中的單位利潤如表3所示。 表3 供不應求情形下實際利潤分配Tab.3 Distribution of actual profits with short supply 由表3可知,產品組合為{1},{2},{3}的零售商在供應商分配所獲得的實際利潤均比零售商{1,3},{2,3}高,因為供應商受到訂貨成本、運輸裝載成本和布料成本因素的影響,單個產品生產會大量減少供應商的其他開支成本,所以供應商更愿意為單個規格數量較多的零售商供貨。 4.2.2 供大于求情形 圖4 供大于求情形下市場的利潤分配Fig.4 Profit distribution in market with oversupply.(a)Directed graph of market fixed profit;(b)Directed graph of market actual profit 通過計算,在供應商對多個零售商最大化利潤分配下,市場得到的最大單位利潤為5.95元/件。在供大于求的環境下,市場環境變為買方市場,零售商成為主導,供應商愿意把貨盡可能銷給零售商,但零售商需要根據自身需求情況進行訂貨。表4示出供大于求情形下實際利潤分配。 表4 供大于求情形下實際利潤分配Tab.4 Distribution of actual profits with oversupply 由表4可看出,產品組合為{1,2,3}的零售商,固定最佳組合是進貨3件服裝,由于市場情況,零售商對裙2所得到的利潤為0,原因是為了保證零售店的產品多樣性,得到最大利潤;從表中同時可看出,零售商{2}獲得的利潤最大,其余是{1},{3},都是單款產品銷售,很大原因是由于存在不同地區消費者的偏愛程度有所差異和市場供大于求,消費者不愿消費導致的。 本文基于服裝的模塊化生產,由供應商提供多款垂直差異化的服裝產品,在消費者效用最大化和零售商利潤最大化情況下,零售商對多款服裝產品進行最優產品組合決策。 通過設計不同的模塊化時尚度,尋找產品組合集合,構建一個有向無環圖,將問題設計為一個最短路徑問題,尋求利潤最大的服裝產品組合,相比于對所有服裝進行窮舉組合決策更加快速有效。本文進一步考慮零售商不同貨架單位固定利潤產生不同的產品組合,分析寡頭供應商對市場最大利潤分配的情況。當供不應求時,供應商為了節省資源,給愿意為產品款式需求較少的零售商配送,市場獲得更大的利潤;當市場供大于求時,服裝零售商根據市場產品時尚度需求對產品進行合理組合。 本文對垂直差異化服裝進行組合優化,為供應商分配和零售商訂貨提供一定的參考,但在本文研究中,只是定義服裝零售商存在貨架空間的單位固定利潤所產生不同的產品組合情況,并沒有對貨架空間進行具體描述,也沒有考慮缺貨影響消費者產生替代的行為,這些都值得進一步探究。 FZXB3.2 服裝產品組合優化決策
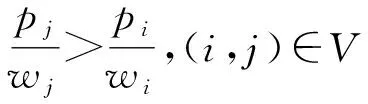
3.3 供應商與零售商之間的最大利潤分配
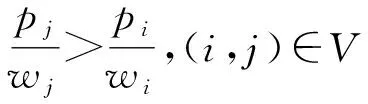
4 算例分析
4.1 服裝垂直差異化最佳產品組合
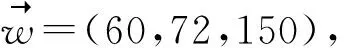
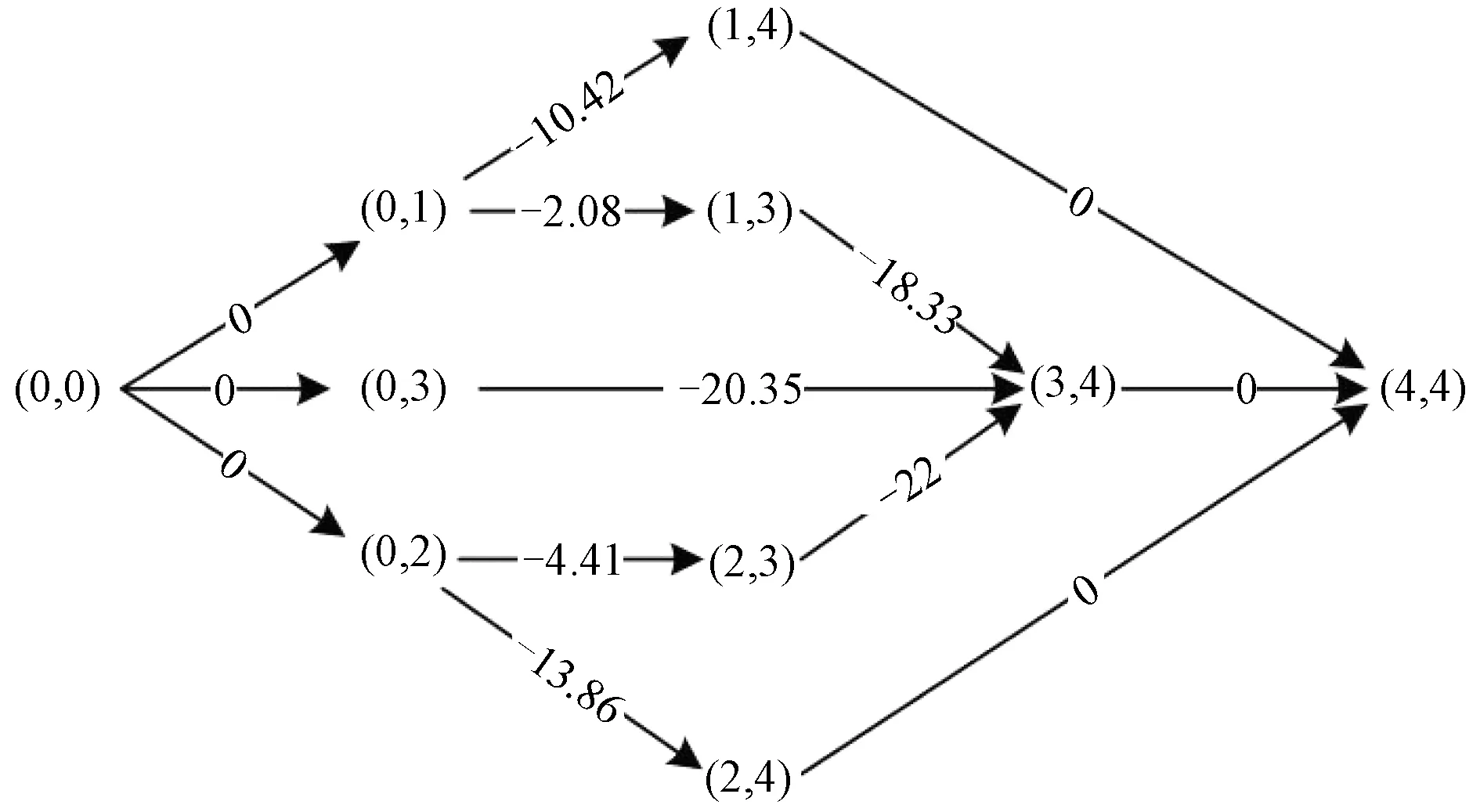

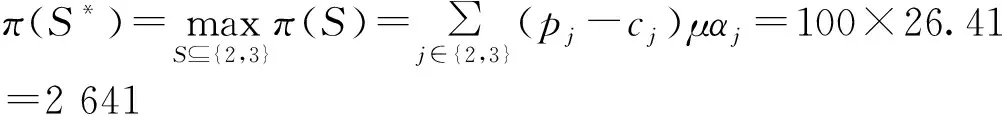
4.2 市場利潤最大化
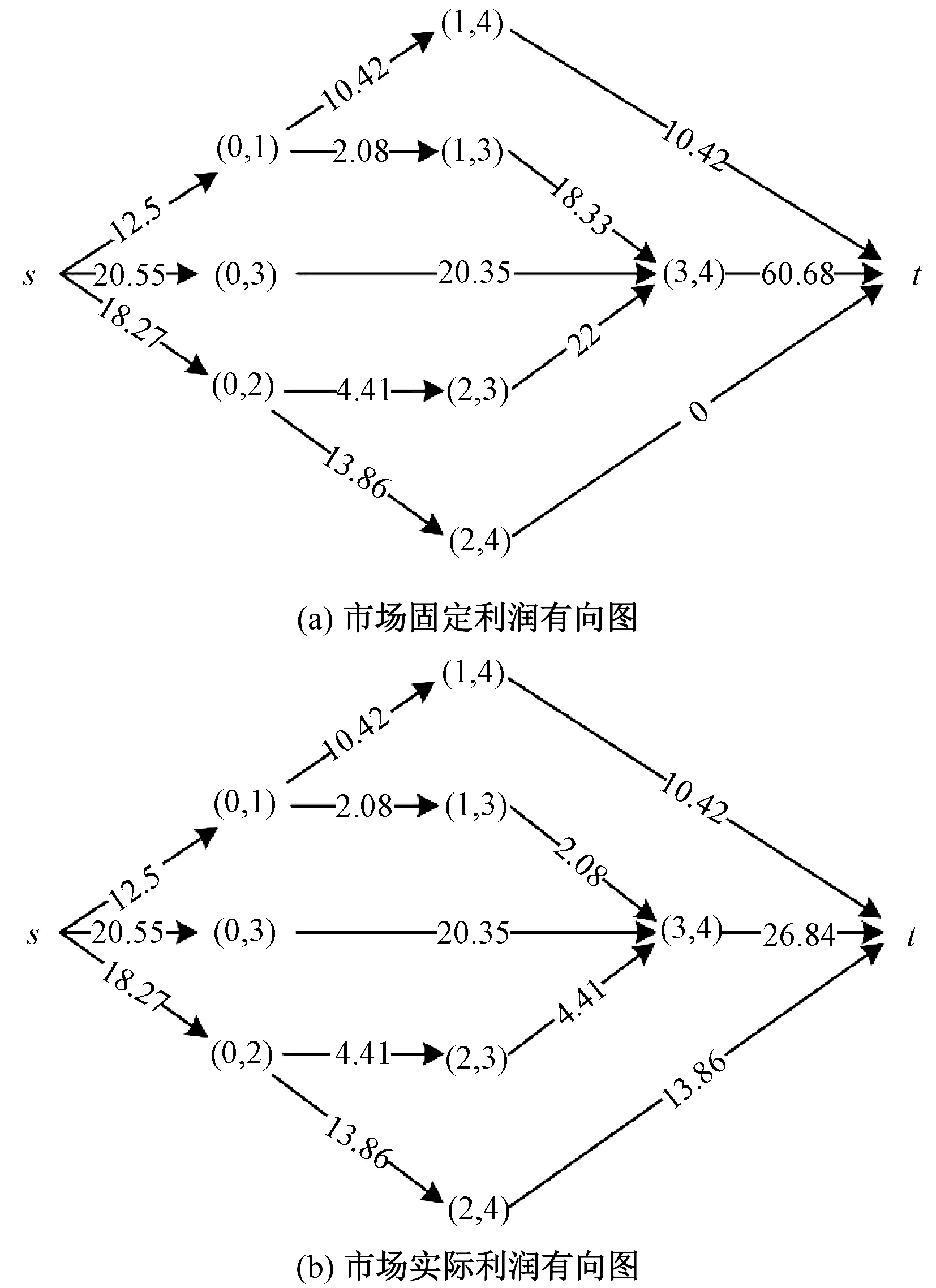

5 結 論

