對不連續帕累托前沿的一種改進的MOEA/D*

張寧 高尚

（江蘇科技大學計算機學院 鎮江 212003）

1 引言

隨著Schaffer［1］提出了第一個多目標進化算法（MOEA），越來越多的人將進化算法應用于求解多目標優化問題。傳統的MOEA主要是基于帕累托支配的思想，例如文獻［2～4］。他們已通過實驗與應用驗證了對處理多目標優化問題的有效性。但是近年來基于分解的MOEAs越來越被人們關注，例如文獻［5～9］。

Zhang和Li最先提出了基于分解的多目標進化算法的框架［5］。相比于基于帕累托最優的方法，大多情況下MOEA/D可以得到更好的帕累托近似前沿，并且其效率也已被證實。自此之后，越來越多的學者對MOEA/D展開了深入的研究：Li和Zhang將差分進化操作應用于MOEA/D［10］；Ke Li提出了一種結合支配與分解的MOEA，通過結合支配和分解的優點以平衡進化的收斂性與多樣性［11］；Xiaoyu He等提出一種基于動態分解的MOEA，使用解本身作為權向量而不是使用預定義的權向量［12］。

雖然MOEA/D對于簡單帕累托前沿的MOP有著非常好的表現，但是對于復雜帕累托前沿的問題，并不能得到一個很好的近似解集。尤其是對于不連續的帕累托前沿問題，MOEA/D得到的近似帕累托前沿，幾乎都會出現近似帕累托前沿分布不均勻以及無法覆蓋完整帕累托前沿的問題。

本文提出了一種改進的MOEA/D解決這些問題。核心思想是使用基于密度的聚類算法判斷是否為不連續帕累托前沿的優化問題。如果是，則將其轉化為數個連續帕累托前沿的優化問題并協同演化。通過權向量重生成和種群重分配解決不均勻和不完整的問題。本文將這種算法命名為MOEA/D-DE-DC。

2 相關知識

2.1 多目標優化問題

在現實世界中存在著許多多目標優化問題（MOP），其可以被定義為

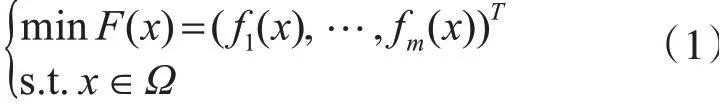
其中x為決策向量，Ω為n維決策空間，F:Ω∈Rm中包含了m個需要同時優化的目標函數，Rm為目標空間。

2.2 MOEA/D

MOEA/D的主要思想是將一個多目標問題通過聚合函數分解為若干個單目標問題，然后同時優化所有的單目標問題。Zhang和Li提出了三種聚合函數：懲罰邊界交叉、加權和以及切比雪夫［5］。在本文中，為了簡單我們選擇使用切比雪夫分解方法，公式如下：

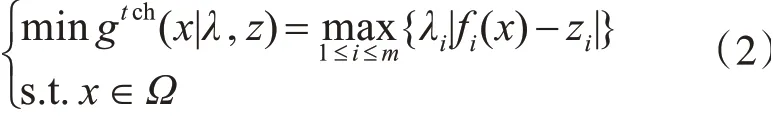
其中λ為權向量，z為參考點。每一個權向量所對應的子問題的最優解就是MOP問題的帕累托最優解，所以可以將所有子問題最優解的集合看作PF的良好近似。

2.3 DBSCAN

DBSCAN是一種經典的基于密度的聚類算法［13］。它具有無需預先設定聚類的數量，可以識別任意形狀的簇等優點。本文中的算法需要在第一階段結束時對得到的近似PF進行聚類，通過聚類的數量判斷是否屬于不連續PF的問題，所以將DBSCAN引入其中。DBSCAN需要的輸入的參數為鄰域半徑ε和正整數MinPts。

3 MOEA/D-DE-DC

3.1 算法的總體框架

算法1為MOEA/D-DE-DC的總體框架。由于我們不知道一個MOP問題的PF是否為不連續的，所以整個算法分為兩個階段。第一階段使用正常的MOEA/D-DE算法，獲得PS和近似PF。第二階段，通過DBSCAN判斷PF是否為不連續的，如果是不連續的，則將種群按聚類劃分，將其轉化為數個連續的PF的子問題并協同演化，最后輸出近似PF。如果是連續的PF則仍然使用第一階段的算法完成演化。

3.2 參考點集的設置

在算法1中步驟8需要為每一個類設置參考點。我們定義這一組參考點為參考點集Z，公式如下：

其中c為通過聚類算法得到的類別數。為了方便后面內容的描述，這里還給出反置參考點集R的定義：

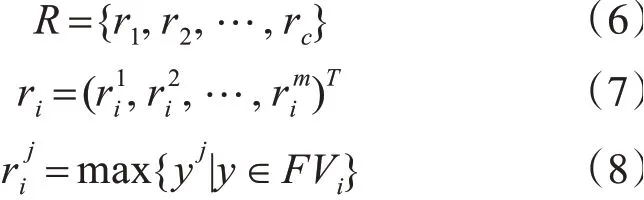
3.3 權向量的重生成和種群的重分配

由于將整個種群劃分為C個子種群，如果C大于1，在第一階段中生成的權向量已經不適用于第二階段了，需要為每一個子種群生成一組新的權向量。而每一個子種群的權向量的個數決定了最終解集的分布。為了解決在第一階段結束帕累托解集分布不均勻的現象，需要通過每一子類種群中目標向量分布空間的大小占總分布空間的比重來衡量其需要生成的權向量的數目，公式如下：

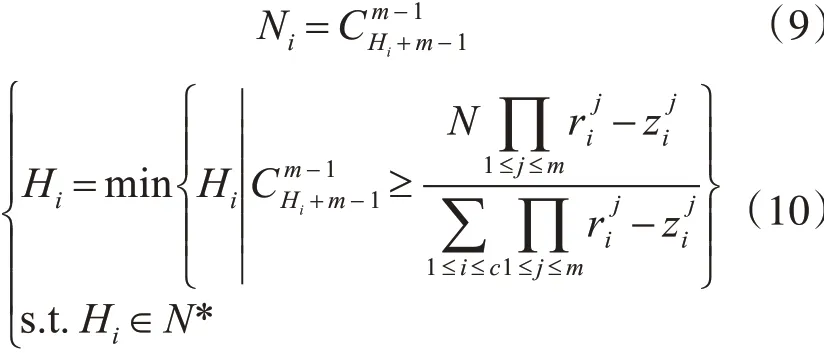
其中Ni為第i個子種群生成權向量的數量，對于每一個子種群的權向量的分解方法仍然使用的是Das和Dennis的方法［14］。第i組權向量的鄰居數量設置為：

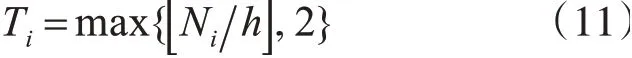
然后將種群重新分配給新生成的數組權向量。不重新生成新的種群，是為了最大程度的利用第一階段的計算資源，加快優化速度。種群重分配的過程如算法3中所示：

這種算法的好處在于可以最大程度地保存種群的多樣性，同時又不會使得某個個體重復的次數過多。在分配個體的時候引入貪心策略，因為種群重分配不需要達到最優，在第二階段的進化中算法可以自行調整。

3.4 種群更新

種群更新的詳細過程如下：

算法3種群更新

輸入：經過聚類的種群x；

經過聚類的近似帕累托前沿FV。

輸出：經過聚類的種群x；

經過聚類的近似帕累托前沿FV。

步驟1 Fori=1，2，…，c，j=1，2，…，NiDo：

步驟1.1選取父代個體：生成一個隨機數u∈[0，1]，然后通過公式4.1設置Q；

步驟1.2生成子代：從Q中隨機選擇兩個索引k與l，將xi、xk和xl使用差分進化算子產生子代個體x′，在通過多項式變異產生x″；

步驟1.3調整：若x″不在鄰域目標可行域中，則重新生成x″；否則計算其所屬子類種群的索引b；

步驟1.4更新參考點zb：對每一個a=1，2，…，m，如果，則將

步驟1.5計算評價函數F(x″)

步驟1.6更新種群：設置o=0，然后：1）如 果o=nr或Q=? ，則 轉 至 步 驟1，否 則 從M={(b，1)，(b，2)，…，(b，Nb)}中隨機選擇一個索引（b，d）；

3）將（b，d）從M中刪除，o=o+1，轉至1）。

步驟2輸出x和FV。

步驟1.1Q的計算公式如下：

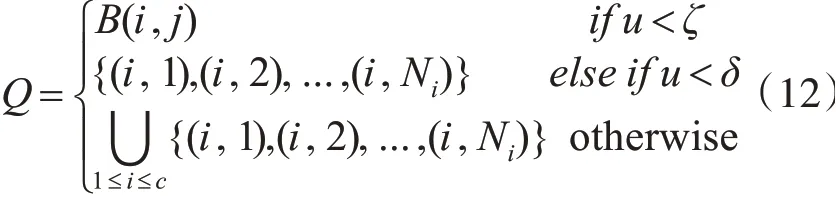
其中u為隨機數，取值范圍為[0，1]；δ，ζ為控制參數，0<ζ<δ<1。

步驟1.3中需要計算鄰域可行目標域。對于i=1，2，…，c，定于第i個子類種群的鄰域目標可行域SPi為

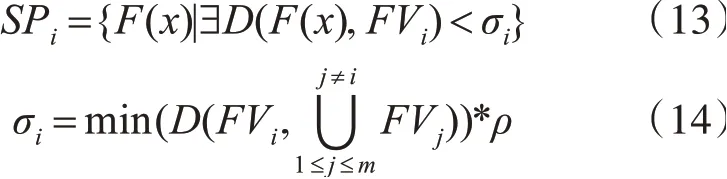
其中ρ表示收縮因子，是控制σi大小的參數，取值范圍為(0，0.5)。

4 實驗結果與分析

4.1 測試函數與對比算法

為了驗證本改進算法的性能。選取了廣泛使用的測試測試函數ZDT，DTLZ，WFG和MOP。其中ZDT1和ZDT2的PF為連續的；其他測試函數的PF均為不連續。MOP4為三目標測試函數，其余測試函數為兩目標。所有測試函數的決策域均為30維。使用MOEA/D-DE與其改進的算法MOEA/D-DE-DC進行對比。

4.2 參數設置

本次實驗使用Matlab2019平臺。操作系統為Win7。為了相對公平，兩算法相同的參數都設為相同的值。所有算法的參數設置如下：

1）DBSCAN的參數設置：MinPts=2，WFG2中ε=0.3，MOP4中ε=0.2，其余ε=0.1。

2）DE算子：CR=1.0，F=0.5。多項式變異算子：η=20，pm=1/n。

3）每個測試函數獨立運行20次。算法在達到最大迭代次數600次后停止運行。

4）兩目標的種群規模為100，三目標的種群規模為300。

5）其他控制參數：Mr=0.75，h=4，ζ=0.3，δ=0.9，T=N/10，nr=2。兩目標問題ρ設為0.35，三目標ρ設為0.3。

4.3 評價指標

本文采用多目標進化算法中最廣泛使用的評價指標，即IGD（Inverted Generational Distance）［15］。IGD可以提供有關所得解集的多樣性與收斂性的可靠信息。設PF為從真實POF均勻采樣的一組解，PF*為目標空間中的一組近似解，IGD的計算公式如下：

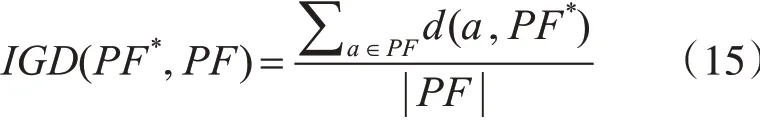
其中d(a，PF*)是a與PF*中所有點的歐幾里德距離的最小值。IGD的值越低表示PF*越趨近與真實PF。本次實驗中所有測試函數從PF中采樣點的數量設置為500。

4.4 性能測試

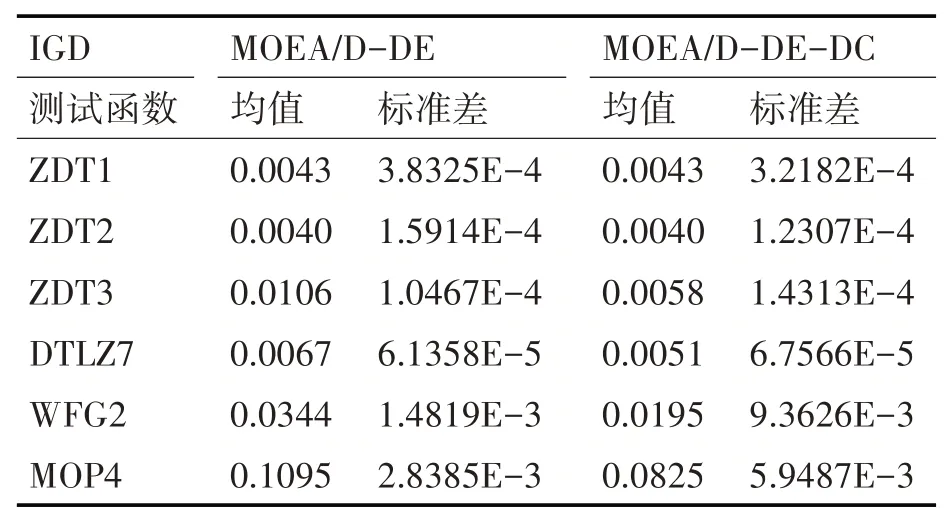
表1 MOEA/D-DE與MOEA/D-DE-DC的IGD

圖1 為兩個算法種群的平均IGD值隨迭代次數變化的折線圖。因為兩個算法前半部分相同所以只截取了從401～600次迭代的數據。從圖中可以看出MOEA/D-DE-DC在不連續的多目標優化問題中在IGD度量方面都表現的更加優秀。其中450次迭代是MOEA/D-DE-DC第一階段與第二階段的分界線。可以看到圖3～圖5在迭代次數450的刻度附近都存在一段尖峰，這是因為種群的重分配一般會對解集的分布產生一定的影響。隨后IGD值都快速地收斂到了一個更低的值，說明本算法對處理不連續PF的問題有很大提升。

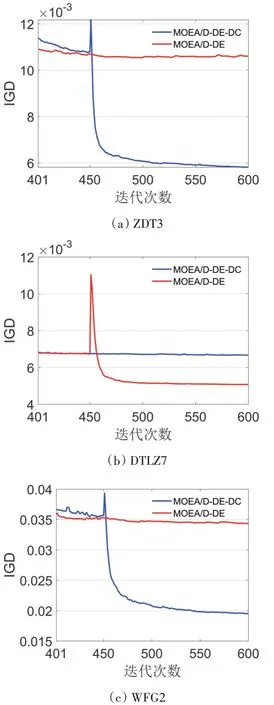
圖1 MOEA/D-DE與MOEA/D-DE-DC的IGD收斂曲線

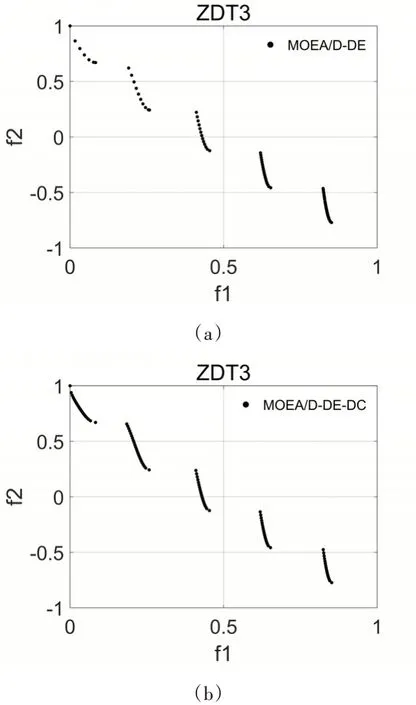
圖2 為兩個算法在個測試函數上得到的近似PF，所有圖均取20次獨立測試的第一次測試數據繪制。由圖可以明顯地看出所有MOEA/D-DE-DC的不連續PF的測試函數獲得的近似PF分布明顯更加均勻與完整。

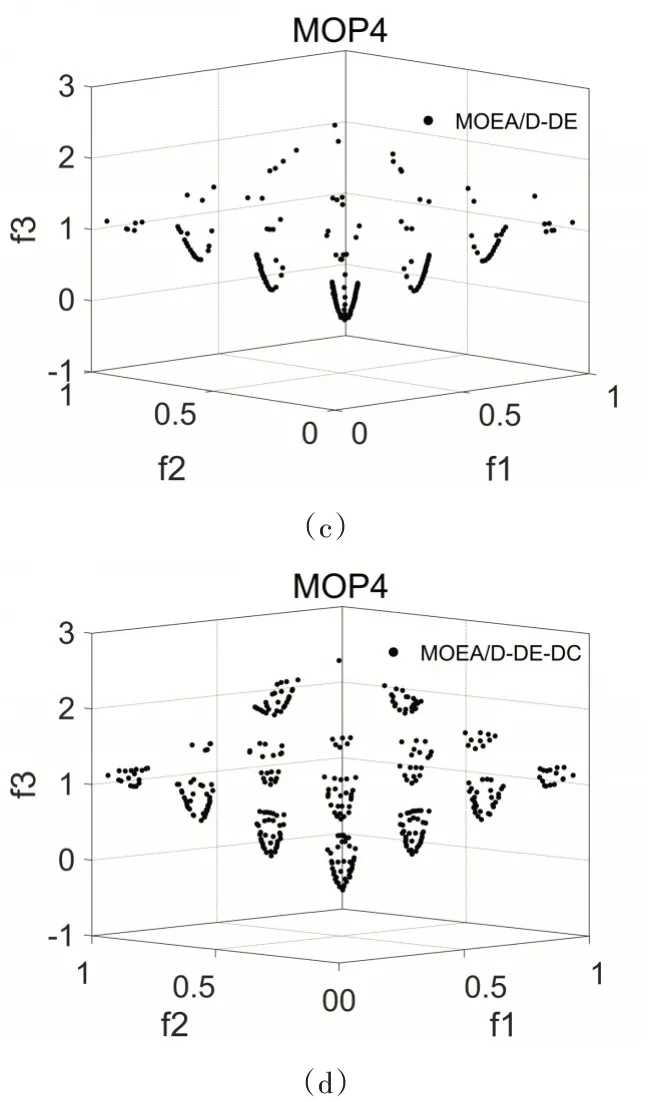
圖2 MOEA/D-DE與MOEA/D-DE-DC在測試函數上的近似帕累托前沿分布圖

5 結語

本文提出了一種改進的MOEA/D，即MOEA/D-DE-DC。其可用于解決不連續PF的多目標優化問題中出現的近似PF不均勻與不完整的問題。將其與未改進的MOEA/D-DE進行對比。實驗結果表明MOEA/D-DE-DC在不連續PF的優化問題中性能有著顯著的提升。通過將不連續的PF問題轉化為數個連續的PF子問題，可以有效地降低PF形狀對算法性能的影響。將來，我們計劃研究MOEA/D解決更多目標以及更復雜PF的MOP的能力。