圓柱形貨物三維裝箱問題簡便解法

賈春玉，樸惠淑，溫 良

(1. 廣東培正學(xué)院 管理學(xué)院, 廣州510830 2. 大連海事大學(xué) 交通運(yùn)輸工程學(xué)院， 遼寧 大連116026) 3. 長春大學(xué) 管理學(xué)院，長春 130022)

一、主要問題

圓柱形貨物平面擺放方式有對齊擺放方式、緊湊壓縫擺放方式和松散擺放方式等形式。三維分層裝箱(擺放)也有對齊擺放方式、緊湊壓縫擺放方式和松散擺放方式等形式。組合擺放比條塊狀貨物擺放得多且復(fù)雜，因此圓柱形貨物三維裝箱問題是比條塊狀貨物裝箱問題更為復(fù)雜的難題。貨物裝箱下料問題的研究成果眾多[1-2]，但針對圓柱形貨物裝箱問題的研究成果非常少，而針對圓柱形貨物三維裝箱問題的研究成果就更少，幾乎查不到相關(guān)的文獻(xiàn)，能查到的相關(guān)文獻(xiàn)多數(shù)為圓形貨物二維下料問題[3-4]，且多數(shù)為遞歸智能解法。雖然裝箱與下料問題互為反問題，有些方法可以互用，但還是有明顯區(qū)別的，其主要區(qū)別是下料問題具有最大毛坯排數(shù)限制、切割寬度損耗等，在許多情況下不能直接互用，因此有必要研究圓柱形貨物裝箱問題。傳統(tǒng)的方法是人們憑經(jīng)驗(yàn)裝箱或下料，存在優(yōu)化程度低、成本高等弊端。為了解決這些問題，學(xué)者們提出了多種解法，如動(dòng)態(tài)規(guī)劃算法[5-6]、啟發(fā)式遞歸解法[7-8]等。這些方法雖然可以解決這類問題，但通常需要建立較為復(fù)雜的數(shù)學(xué)模型和編制求解軟件進(jìn)行求解，不易掌握。為了更好地解決這一問題，本文提出新的線性規(guī)劃解法，該方法簡單、易于掌握、優(yōu)化程度高。因?yàn)榫o湊壓縫擺放方式優(yōu)化程度通常較高、貨垛穩(wěn)定、擺放規(guī)律性強(qiáng)、擺放效率高，所以這里只針對這種擺放方式提出新的簡便解法。

(一)豎立擺放時(shí)三維裝箱解法

貨物有時(shí)要求必須豎立擺放，尤其是圓柱形容器裝滿貨物時(shí)更是如此。在這種情況下，三維裝箱相對比擺放無約束時(shí)簡單，只需按要求優(yōu)化求解出按貨箱高度方向豎立擺放一層的優(yōu)化數(shù)量，再乘以貨箱按高度方向能擺放的層數(shù)即可。因此，首先是求解出平面二維優(yōu)化擺放數(shù)量，然后計(jì)算出能擺幾層，最后根據(jù)兩者乘積得出總的擺放數(shù)量。

單一圓柱形貨物平面放的三種擺放方式在一定條件下均可能是最佳擺放方式。在擺放方式的組合上，可以是單一一種擺放方式，也可以是兩種或兩種以上擺放方式的組合，垛高方向可以是與貨箱長度方向相同，也可以是與貨箱寬尺寸方向相同，擇優(yōu)作為最終優(yōu)化方案，獲得平面擺放近似最優(yōu)解，據(jù)此獲得三維擺放近似最優(yōu)解。

(二)擺放無約束時(shí)三維裝箱解法求解思路

總體求解思路是分別按貨箱長J1、寬J2和高J3三個(gè)維度優(yōu)化擺放，將三個(gè)維度優(yōu)化方案擇優(yōu)為最終優(yōu)化方案，獲得滿意近似最優(yōu)解。每個(gè)維度優(yōu)化時(shí)可分為兩個(gè)階段，以最終按貨箱高度優(yōu)化為例，求解過程分為兩個(gè)階段：第一階段是求出按貨物直徑和高度尺寸每擺一層的優(yōu)化擺放數(shù)量；第二階段是按貨箱高尺寸三維優(yōu)化求解。第一階段的求解步驟為：計(jì)算貨物兩個(gè)維度的尺寸(直徑和高度)每層擺放數(shù)量，即在貨箱長和寬的二維平面內(nèi)，先計(jì)算按貨物直徑尺寸擺放一層的優(yōu)化擺放數(shù)量，此時(shí)的貨物可用尺寸是直徑和高度，暫時(shí)把貨物直徑尺寸視為矩形貨物的長(H1)，貨物高度尺寸視為貨物的寬(H2)，貨箱可用尺寸是貨箱的長和寬，選用一種或幾種優(yōu)化擺放方式進(jìn)行優(yōu)化求解，擇優(yōu)得出按貨物直徑尺寸擺放一層的數(shù)量；再計(jì)算按貨物高度(如桶高)擺放一層的優(yōu)化擺放數(shù)量，此時(shí)的貨物可用尺寸是直徑，貨箱可用尺寸是貨箱的長和寬，選用一種或幾種優(yōu)化擺放方式進(jìn)行優(yōu)化求解，擇優(yōu)得出一層貨物高的擺放數(shù)量。第二階段的求解步驟為：按貨物直徑擺放一層和按貨物高度擺放一層的優(yōu)化擺放數(shù)量，再按貨箱高度進(jìn)行三維立體優(yōu)化擺放，優(yōu)化求解各擺多少層，使總的擺放數(shù)量最多，得出近似最優(yōu)解。其他兩個(gè)維度(按貨箱的長和寬)優(yōu)化類似，三個(gè)維度優(yōu)化結(jié)果擇優(yōu)作為最終優(yōu)化結(jié)果。

(三)求解過程

以按貨箱高度三維立體優(yōu)化為例，詳細(xì)介紹求解過程。其他兩個(gè)維度優(yōu)化與高度優(yōu)化類似，所以只作概略介紹，只介紹第二階段求解的數(shù)學(xué)模型。

1.按貨箱高度三維優(yōu)化求解過程

(1)第一階段求解過程及數(shù)學(xué)模型。擺放方式有單一緊湊擺放方式、組合緊湊擺放方式、單一松散擺放方式和組合松散擺放方式；優(yōu)化方法有數(shù)量優(yōu)化方法[9]、邊長優(yōu)化方法[9]、5塊法[10]、線性規(guī)劃解法和非線性規(guī)劃解法等。這里只介紹最簡單、擺放效率最高的單一緊湊擺放方式，雖然該方法優(yōu)化程度略低，但簡單、實(shí)用、裝箱效率高。

首先，按貨箱長二維優(yōu)化時(shí)規(guī)劃求解數(shù)學(xué)模型。

單一緊湊擺放方式是指貨物在平面內(nèi)只有一種擺放方式，如壓縫擺放方式1(按貨箱長J1優(yōu)化擺放，即垛高為貨箱長J1方向)；壓縫擺放方式2(按貨箱寬J2優(yōu)化擺放，即垛高為貨箱寬J2方向)，列出優(yōu)化數(shù)學(xué)模型求解，兩種擺放方式優(yōu)化程度擇優(yōu)作為優(yōu)化結(jié)果。

模型1：按貨箱長二維優(yōu)化時(shí)按貨物直徑尺寸擺一層的數(shù)學(xué)模型

設(shè)貨物“長”為(直徑)H1=2R，“寬”(貨物高)為H2；貨物“長”對貨箱長擺放個(gè)數(shù)為N11，對貨箱寬擺放個(gè)數(shù)為N12；貨物“寬”對貨箱長擺放個(gè)數(shù)為N21，對貨箱寬擺放個(gè)數(shù)為N22。X11為貨物“長”擺放的列數(shù)(按貨箱長方向擺放個(gè)數(shù))，X21為貨物“寬”擺放的列數(shù)(按貨箱長度方向擺放個(gè)數(shù))，總的擺放數(shù)量為ZQ1。為了簡化問題，暫不考慮剩余空間可擺放數(shù)量(計(jì)算例題中考慮了)，則數(shù)學(xué)模型如下[9]。

目標(biāo)函數(shù)：MaxZQ1=X11×N22+X21×N12

約束條件:X11×H1+X21×H2≤J1

X11、X21為正整數(shù)。

在符號Nij中，i代表貨物維度，1代表貨物的“長”，2代表貨物的“寬”; j代表貨箱維度，1代表貨箱長，2代表貨箱寬。則有如下計(jì)算公式：

Nij=[Jj/Hi]1

符號“[ ]1”代表向下取整。

例如:N12= [J2/H1]1，代表貨物“長”在貨箱“寬”方向上最多可擺放的個(gè)數(shù)。

模型2：按貨箱長二維優(yōu)化時(shí)按貨物高擺一層的數(shù)學(xué)模型

圓柱形貨物半徑R，對齊擺放一層高度為2R(參見圖1，參見圖2和圖3，帶方格線部分)、壓縫單數(shù)和雙數(shù)層一層高度為H(參見圖2和圖3，帶底色為壓縫單數(shù)層，無底色、無方格線為雙數(shù)層)，對齊擺放、壓縫單數(shù)擺放和壓縫雙數(shù)擺放層對應(yīng)3個(gè)變量。設(shè)按貨箱長度J1優(yōu)化時(shí)(壓縫擺放方式1)圓柱形貨物對齊擺放、壓縫單數(shù)層、壓縫雙數(shù)層3個(gè)變量分別為X11、X21、X31, 按貨箱寬尺寸方向貨物對齊、壓縫單數(shù)層、壓縫雙數(shù)層每層擺放個(gè)數(shù)(已知數(shù))分別為N11、N21、N31, 總的擺放數(shù)量為GQ1，則數(shù)學(xué)模型如下。

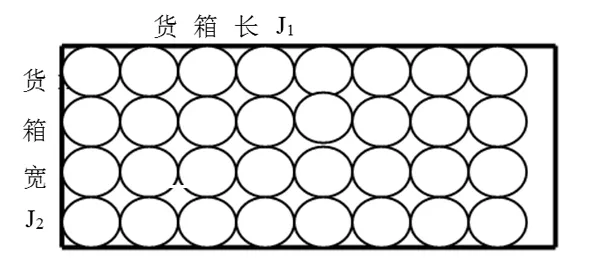
圖1 上下對齊擺放方式

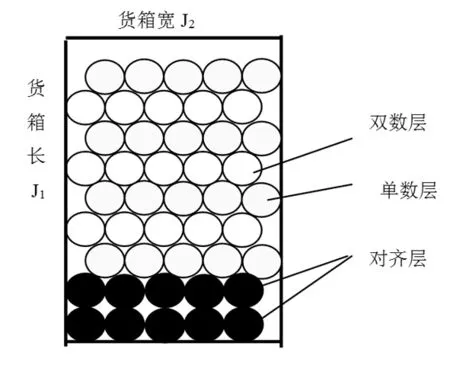
圖2 壓縫擺放方式1

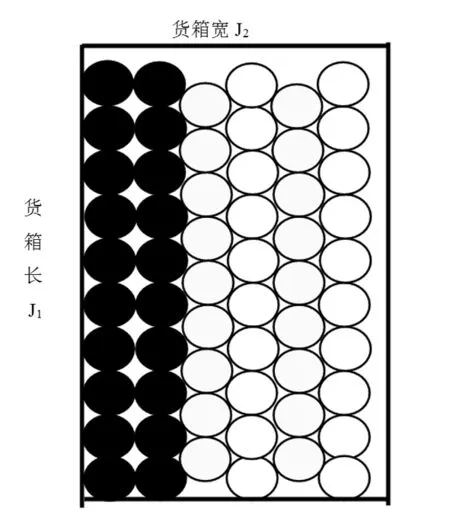
圖 3 壓縫擺放方式2

目標(biāo)函數(shù)：MaxGQ1=X11×N11+X21×N21+X31×N31

S．T．X11×2R+X21×H+X31×H≤J1

X21≥X31

X21-X31≤1

X11≥1

變量為非負(fù)整數(shù)。

其中，H=30.5R，N11= N31=[J2/2R]1,N21=[(J2-R)/2R]1; 變量Xij和Nij中的下角標(biāo)i代表第i個(gè)變量(i=1，2，3)，1、2、3分別代表對齊、壓縫單數(shù)、壓縫雙數(shù)層；j代表貨箱維度(j=1，2)，1和2分別代表按貨箱長度J1和寬度J2優(yōu)化時(shí)的對應(yīng)變量或擺放個(gè)數(shù)。以下類似符號代表意義相同。

其次，按貨箱寬二維優(yōu)化時(shí)規(guī)劃求解數(shù)學(xué)模型。

模型1：按貨箱寬二維優(yōu)化時(shí)按貨物直徑擺一層的數(shù)學(xué)模型

設(shè)X12為貨物“長”擺放的列數(shù)(按貨箱寬尺寸方向擺放個(gè)數(shù))，X22為貨物“寬”擺放的列數(shù)(按貨箱寬尺寸方向擺放個(gè)數(shù))，總的擺放數(shù)量為ZQ2。為了簡化問題，暫不考慮剩余空間可擺放數(shù)量(計(jì)算例題中考慮了)，則數(shù)學(xué)模型如下[9]。

目標(biāo)函數(shù)：MaxZQ2=X12×N21+X22×N11

約束條件:X12×H1+X22×H2≤J2

X12、X22為正整數(shù)。

模型2：按貨箱寬二維優(yōu)化時(shí)按貨物高擺一層的數(shù)學(xué)模型

設(shè)按貨箱寬J2優(yōu)化時(shí)(壓縫擺放方式2), 圓柱形貨物對齊擺放、壓縫單數(shù)層個(gè)數(shù)、壓縫雙數(shù)層個(gè)數(shù)3個(gè)變量分別為X12、X22、X32，按貨箱長度方向貨物對齊、壓縫單數(shù)層、壓縫雙數(shù)層每層擺放個(gè)數(shù)(已知數(shù))分別為N12、N22、N32，總的擺放數(shù)量為GQ2，則數(shù)學(xué)模型如下。

目標(biāo)函數(shù)：MaxGQ2=X12×N12+X22×N22+X32×N32

S．T．X12×2R+X22×H+X32×H≤J2

X22≥X32

X22-X32≤1

X12≥1

變量為非負(fù)整數(shù)。

其中，H=30.5R，N12= N32=[J1/2R]1、N22=[ (J1-R)/2R]1，符號“[ ]1”為向下取整。

最后，最終二維優(yōu)化結(jié)果。

按貨物高擺一層最終優(yōu)化結(jié)果(GQ3)：

GQ3=Max(GQ1，GQ2)

按貨物直徑擺一層最終優(yōu)化結(jié)果(ZQ3)：

ZQ3=Max(ZQ1，ZQ2)

(2)第二階段求解過程及數(shù)學(xué)模型。設(shè)按貨箱高尺寸三維優(yōu)化時(shí)貨物直徑尺寸擺X1層，貨物高尺寸擺X2層，優(yōu)化擺放數(shù)量為Q3，則按貨箱高尺寸三維優(yōu)化時(shí)數(shù)學(xué)模型如下[9]。

目標(biāo)函數(shù)：MaxQ3=X1×ZQ3+X2×GQ3

約束條件:X1×H1+X2×H2≤J3

H1=2R

X1、X2為正整數(shù)。

2.按貨箱寬尺寸優(yōu)化求解過程

按貨箱寬尺寸優(yōu)化求解過程與按貨箱高尺寸優(yōu)化求解過程類似，只需把平面二維優(yōu)化時(shí)的貨箱尺寸換成貨箱長和高的尺寸，再按貨箱寬尺寸進(jìn)行三維優(yōu)化，優(yōu)化結(jié)果為Q2，設(shè)ZQ2和GQ2分別為按貨箱寬尺寸三維優(yōu)化時(shí)按貨物直徑和高度尺寸平面優(yōu)化擺放數(shù)量。為了節(jié)省篇幅，第一階段求解過程及數(shù)學(xué)模型從略，設(shè)按貨箱寬尺寸三維優(yōu)化時(shí)貨物直徑尺寸擺X1層、貨物高尺寸擺X2層，則按貨箱寬尺寸三維優(yōu)化時(shí)的數(shù)學(xué)模型如下[9]。

目標(biāo)函數(shù)：MaxQ2=X1×ZQ2+X2×GQ2

約束條件:X1×H1+X2×H2≤J2

H1=2R

X1、X2為正整數(shù)。

3.按貨箱長尺寸優(yōu)化求解過程

按貨箱長尺寸優(yōu)化求解過程與按貨箱高尺寸優(yōu)化求解過程類似，只需把平面二維優(yōu)化時(shí)的貨箱尺寸換成貨箱寬和高的尺寸，再按貨箱長尺寸進(jìn)行三維優(yōu)化，優(yōu)化結(jié)果為Q1，設(shè)ZQ1和GQ1分別為按貨箱長三維優(yōu)化時(shí)按貨物直徑和高度尺寸平面優(yōu)化擺放數(shù)量。為了節(jié)省篇幅，第一階段求解過程及數(shù)學(xué)模型從略，設(shè)按貨箱長尺寸三維優(yōu)化時(shí)貨物直徑尺寸擺X1層，貨物高尺寸擺X2層，則按貨箱長尺寸三維優(yōu)化時(shí)的數(shù)學(xué)模型如下[9]。

目標(biāo)函數(shù)：MaxQ1=X1×ZQ1+X2×GQ1

約束條件:X1×H1+X2×H2≤J1

H1=2R

X1、X2為正整數(shù)。

4.最終三維優(yōu)化結(jié)果

取按貨箱三維優(yōu)化結(jié)果最好的作為最終優(yōu)化結(jié)果ZQ。

ZQ=Max(Q1，Q2，Q3)

最優(yōu)解下限LQ=[(J1×J2×J3)/(3.14159×R2×H2)]1

優(yōu)化程度=(ZQ/LQ) ×100%

二、求解實(shí)例

實(shí)例1: 貨箱長(J1)1200cm，寬(J2)234cm，高(J3)269cm,貨物為半徑(R)21cm的圓柱形，圓柱高(H2)31cm，問圓柱形貨物擺放無約束情況下最多能擺多少貨物？

解：最優(yōu)解下限LQ=[(1200×234×269)/(3.14159×212×31)]1=1758, 經(jīng)計(jì)算得知，在三維立體優(yōu)化中按貨箱寬尺寸三維優(yōu)化最好，所以二維優(yōu)化時(shí)只用到貨箱長和高的尺寸。在貨箱長和高的二維優(yōu)化中，用數(shù)量優(yōu)化方法按貨物直徑尺寸擺放一層時(shí)按貨箱高尺寸優(yōu)化擺放最多，按貨物直徑每一列可擺38個(gè)，優(yōu)化擺4列；按貨物高尺寸每一列可擺28個(gè)，優(yōu)化擺3列，兩種擺放方式優(yōu)化組合一共擺236個(gè)。按貨物高尺寸擺放一層時(shí)，按貨箱高尺寸優(yōu)化擺放最多，在二維擺放中對齊層每層擺放28個(gè)，優(yōu)化擺放2層；單數(shù)層每層擺放28個(gè)，優(yōu)化擺放3層；雙數(shù)層每層擺放28個(gè)，優(yōu)化擺放2層，按貨物高尺寸擺一層時(shí)優(yōu)化組合共可擺196個(gè)。

在三維立體優(yōu)化中，按貨箱寬尺寸優(yōu)化，按圓柱直徑尺寸每層可擺236個(gè)，優(yōu)化擺1層；按圓柱高尺寸每層可擺196個(gè)，優(yōu)化擺6層：兩種方式共可擺1412個(gè)，優(yōu)化程度為80.32%。而用其他優(yōu)化方法(如5塊法[10])，在二維平面優(yōu)化中按貨物直徑尺寸擺放一層時(shí)，按貨箱高尺寸優(yōu)化擺放最多，可擺239個(gè)，比簡便解法多3個(gè)；按貨物高尺寸擺放數(shù)量一樣，三維立體優(yōu)化也是按貨箱寬尺寸優(yōu)化最好，可擺1415個(gè)，優(yōu)化程度為80.49%，僅多0.17%，差別不大。

實(shí)例2: 貨箱長(J1)960cm，寬(J2)234cm，高(J3)242cm,貨物為半徑(R)16cm的圓柱形，圓柱高(H2)40cm，問圓柱形貨物擺放無約束情況下最多能擺多少貨物？

解：最優(yōu)解下限LQ=[(960×234×242)/(3.14159×162×40)]1=1689, 經(jīng)計(jì)算得知，在三維立體優(yōu)化中按貨箱高尺寸三維優(yōu)化最好，所以二維平面優(yōu)化中只用到貨箱長和寬的尺寸。二維優(yōu)化時(shí)，用數(shù)量優(yōu)化方法按貨物直徑尺寸擺放一層時(shí)按貨箱寬尺寸優(yōu)化擺放最多，按貨物直徑每一列可擺24個(gè)，優(yōu)化擺6列；按貨物高度尺寸每一列可擺30個(gè)，優(yōu)化擺1列：兩種方式優(yōu)化組合共擺174個(gè)。按貨物高尺寸擺放一層時(shí)，按貨箱寬尺寸優(yōu)化擺放最多，在二維擺放中對齊層每層擺放30個(gè)，優(yōu)化擺放2層；單數(shù)層每層擺放29個(gè)，優(yōu)化擺放3層；雙數(shù)層每層擺放30個(gè)，優(yōu)化擺放3層，按貨物高尺寸擺一層時(shí)優(yōu)化組合共可擺237個(gè)。

在三維立體優(yōu)化中，按貨箱高尺寸三維優(yōu)化，按圓柱直徑尺寸每層可擺174個(gè)，優(yōu)化擺0層；按圓柱高尺寸每層可擺237個(gè)，優(yōu)化擺6層：兩種方式優(yōu)化組合共可擺1422個(gè)，優(yōu)化程度為84.19%。而用其他優(yōu)化方法(如5塊法[10])，也是按貨箱高尺寸優(yōu)化最好，可擺1422個(gè)，優(yōu)化程度為84.19%，結(jié)果一樣。

三、結(jié)論

根據(jù)圓柱形貨物的特點(diǎn)及緊湊壓縫擺放方式優(yōu)化程度高、貨垛穩(wěn)定、擺放規(guī)律性強(qiáng)、擺放效率高等特點(diǎn)，為了克服現(xiàn)有圓柱形貨物二維裝箱問題解法相對復(fù)雜、不易掌握、三維立體裝箱缺乏有效解法困境，提出新的簡便線性規(guī)劃解法。經(jīng)比較，雖然優(yōu)化程度有時(shí)比非線性規(guī)劃解法略低，但結(jié)果仍然相當(dāng)理想，可有效克服非線性規(guī)劃解法求解時(shí)間長、經(jīng)常出現(xiàn)局部最優(yōu)解、求解效率低等弊端。新的線性規(guī)劃解法相對簡單、容易理解、易于掌握、優(yōu)化程度高，求解效率也高，運(yùn)用Excel軟件就可快速求解，可有效解決圓柱形貨物擺放無約束這類復(fù)雜NP難問題。