異構集群系統分布式自適應輸出時變編隊跟蹤控制

田 磊 董希旺 ,2 趙啟倫 李清東 呂金虎 ,2 任 章 ,2

集群系統中個體之間通過局部的感知和簡單的行為交互,可以在宏觀上涌現出更為復雜與高級的群體行為,即集群智能.生物界中有很多集群智能的例子:鳥群利用上洗氣流編隊飛行,可以降低飛行阻力,實現遠距離大范圍遷徙;狼群通過協同圍捕,利用時空優勢,能夠以弱勝強,捕食大型獵物;蟻群通過協同搬運,可以充分彌補個體力量薄弱的劣勢,以小博大,提高覓食效率.軍事領域也有很多通過集群協同方式提升作戰效能的例子:多個微納衛星通過協同可以構建一個虛擬衛星,實現深空探測及高精度三維成像等復雜功能,完成單個衛星無法完成的任務;多架低成本無人機通過協同方式可以實施蜂群作戰模,使敵方高價值防空體系的火力通道陷入飽和,進而大幅度提高突防能力、毀傷能力和作戰效費比.正是因為集群智能可以實現上述1+1?2的效果,近年來備受學者關注.編隊控制作為集群智能的重要基礎性研究分支,也涌現出了較為豐富的研究成果.早期的編隊控制方法主要是集中式,即存在中心節點,且對通信拓撲要求高.隨著一致性理論的發展,分布式編隊控制方法以其不依賴中心節點、具備良好的可擴展性等優點,取得了長足的發展[1].研究的方向從固定編隊[2]擴展到時變編隊[3?4],研究的內容從普通編隊控制[5?6]發展到編隊跟蹤控制[7?8]、編隊合圍控制[9?10]等,研究的模型也逐漸豐富,包括了線性系統[11]、非線性系統[12?13]、同構系統[14]、異構系統[15?16]等,研究的通信拓撲也涵蓋無向拓撲、有向拓撲、連續性拓撲、非連續性拓撲、拓撲固定、拓撲切換等[17?20].不僅如此,研究的編隊穩定性問題也從漸近穩定問題逐漸發展到有限時間穩定問題甚至固定時間穩定問題[21?22].隨著研究的深入,如何盡可能減少編隊控制所需的全局信息成為分布式控制的研究重點,如文獻[3]、[8]、[10]、[17]、[19]中設計控制協議參數時需要計算與通信拓撲相關的拉普拉斯矩陣的特征值,文獻[16]、[17]、[19]、[21]中構造控制協議時需要用到領導者輸入的上界值.此外,文獻[2?22]中時變編隊函數是需要設定的全局信息,也并非分布式實時可調控的.

基于上述分析可知,編隊控制方法在理論上尚有許多可以研究和改進的地方.同時,由于理論研究通常受實際應用驅動,根據不同的任務場景,實際應用中期望集群系統的智能體模型既可以是同構的(無人機蜂群作戰任務場景),也可以是異構的(空地/空海協同搜索任務場景),而考慮到強對抗博弈和強電磁干擾帶來的影響,還期望通信拓撲是有向切換的,并且實際應用中陣風、紊流等未知外部擾動也是不可忽略的因素.需要指出的是,在研究編隊跟蹤問題時,跟隨者跟蹤的領導者通常分為合作目標和非合作目標.所謂合作目標是指領導者與跟隨者之間存在協同合作關系,通常情況下,領導者為己方可控目標,其控制輸入大多是已知可獲取的.所謂非合作目標是指領導者與跟隨者之間不存在協同合作關系,通常情況下,領導者為非己方不可控目標,其控制輸入大多是未知不易獲取的.經過文獻調研發現,目前尚無研究成果能夠解決高階異構集群系統在領導者存在已知或未知控制輸入、領導者和跟隨者均存在未知擾動、有向通信拓撲存在切換等多種因素并存的情況下的輸出時變編隊跟蹤控制問題.

受上述理論研究和工程應用價值的激勵,本文研究了高階異構集群系統的時變編隊跟蹤控制問題.主要創新有以下兩點:1)集群系統中所有智能體均采用異構模型,同時研究了領導者存在已知和未知控制輸入兩種情況.需要說明的是,考慮到異構集群系統中智能體的動力學模型可能完全不同,當領導者的控制輸入是已知時,可以在領導者層和跟隨者層構造對自身狀態的觀測器,基于該觀測器構造的控制協議不需要利用領導者的全部狀態,只需要利用領導者的輸出信息.而在領導者的控制輸入是未知時,無法通過領導者的輸出信息得到其全部狀態信息,進而需要某個跟隨者能夠獲取領導者的全部狀態信息.2) 在上述領導者存在已知或未知控制輸入的情況下,進一步考慮領導者和跟隨者存在未知擾動以及有向通信拓撲存在切換等多種因素并存對集群系統的影響,結合觀測器理論、自適應理論和滑模控制理論,構造了完全分布式的控制協議,所有跟隨者均不需要獲取領導者輸入的上界值,也不需要利用與通信拓撲相關的拉普拉斯矩陣的特征值,此外,協議中還針對時變編隊函數設計了分布式觀測器,使其不再是全局信息,成為分布式實時可調控的.由于本文研究的集群系統均采用有向通信拓撲,因此極大降低了集群系統對通信帶寬需求.綜上所述,本文研究的內容兼具理論研究與工程應用價值.考慮到有人?無人機協同飛行(領導者為合作目標,見圖1)和空地協同圍捕打擊(領導者為非合作目標,見圖2)等任務場景下,集群系統中個體間動力學模型差異較大即異構模型,同時強電磁干擾時的通信限制和強對抗博弈時外界環境的不確定干擾為集群系統的協同控制帶來了一定的困難,因此本文研究的方法能夠為實戰場景下的分布式 協同控制提供有力的理論支撐和技術保障.

圖1 有人?無人飛行器協同飛行示意圖Fig.1 The illustration of cooperative flight strategy for manned and unmanned aerial vehicles

圖2 空地協同圍捕目標示意圖Fig.2 The illustration of hunting target by air-ground collaboration

1 預備知識和問題描述

1.1 圖論知識

集群系統的通信拓撲關系對應的數學基礎即為圖論知識中關于拉普拉斯矩陣的相關知識.假設集群系統中含有q個智能體,智能體g和智能體k之間存在著從k到g的有向通信,則wgk=1,否則wgk=0.定義鄰接矩陣為W=[wgk]∈Rq×q,定義度矩陣為D=,g=1,2,···,q},定義拉普拉斯矩陣為L=D?W.如果在集群系統的通信拓撲中,某個智能體r到其他所有智能體都存在至少一條有向連接,則稱集群系統的通信拓撲中存在一個以 智能體r為根節點的生成樹.

1.2 問題描述

假設集群系統中含有 1 個領導者和N個跟隨者,不失一般性,所有智能體采用如下異構模型:

通過上述異構模型可知,集群系統中所有智能體的動力學模型可以完全不同.為實現集群系統的輸出編隊,假定所有智能體的輸出具有相同的維度,即pi=p(i=1,2,···,1+N).同時為方便后續表達,領導者標號為1,跟隨者標號為2,3,···,1+N.

假設 1[16].集群系統的通信拓撲包含一個以領導者為根節點的生成樹,且領導者與跟隨者之間的通信方式是單向的,方向是從領導者到跟隨者,不同跟隨者之間的通信方式可以是單向的,也可以是雙向的.

定義集群系統的通信拓撲在固定時間間隔內保持不變,該時間間隔被稱為駐留時間,記為α,其最小值被稱為最小駐留時間,記為αmin.定義t=t0=0為初始時刻,t=tβ(β=0,1,2,···) 為通信拓撲發生變化的時刻,稱為切換時刻.如果假設1 成立,則系統在 [tβ,tβ+1)內的拉普拉斯矩陣Lβ有如下形式:

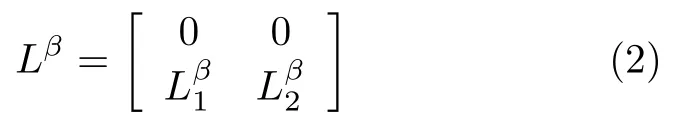
為了前后表達方式的連貫性,后續帶有上標β的變量都表示其位于由區間 [tβ,tβ+1) 定義的時間間隔內.

假設 2.矩陣方程組(3)存在對解矩陣 (Rg,Sg),同時矩陣方程(4)存在解矩陣Tg.

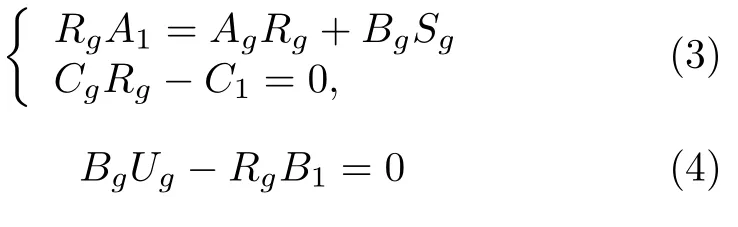
其中,g=2,3,···,1+N.

注1.假設2 要求方程(3)和(4)有解,其可解性是異構集群系統實現輸出編隊跟蹤的必要條件,其物理意義是領導者的已知或未知輸入能夠通過跟隨者的控制輸入ug(t) 進行補償.該假設與文獻[16]中的假設3 和假設4 類似,由參考文獻[16]中的注釋3 可知,式(3)的可解性是異構集群系統能夠實現輸出調節的必要條件[23?27],式(4)的可解性類似采用魯棒控制方法時匹配條件[28?29],因此假設2 是合理的.

假設 3.所有智能體的控制輸入和未知擾動是有界的,即滿足‖ui‖1≤χ,‖di‖1≤,χ和為未知正實數,同時未知擾動滿足limt→∞di(t)存在.

注2.實際物理系統中智能體的控制輸入和未知擾動是有界的,但是其界限值通常不易獲取,假設3 要求擾動的極限存在是由于下文中設計控制協議時借鑒了文獻[30]中擾動觀測器的設計方法,此假設為文獻[30]中擾動觀測器能夠收斂的前提條件.需要說明的是,針對不同于假設2 的擾動形式,下文中的注釋4 給出了相應改進方案,因此假設3是合理的.

定義 1.如果通信拓撲如假設1 所述,且對于任意有界初始狀態,等式(5)成立,則稱異構集群系統能夠實現有向拓撲切換條件下的輸出時變編隊跟蹤.

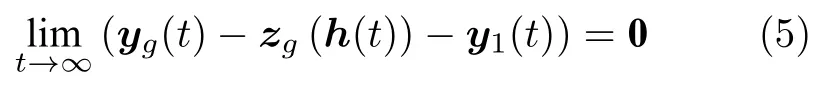
其中,g=2,3,···,1+N,zg(h(t)) 為由h(t) 定義的時變向量,可以表征跟隨者之間輸出編隊的隊形以及整個編隊隊形與領導者之間的相對關系.

由定義1 可知,集群系統的輸出時變編隊跟蹤隊形刻畫為以h(t)為自變量zg(h(t)) 為因變量的復合向量函數,與現有研究時變編隊的文獻[2?22]不同,h(t) 不是固化的全局信息,而是由領導者或與領導者存在直接拓撲連接的跟隨者調控的時變向量.后續將構造分布式觀測器對其進行估計,估計值記為.顯然,如果,則.假設輸出是1 維的,根據式(5) 所描述的等式關系,圖3 給出了二維XOY平面內集群系統輸出時變編隊跟蹤示意圖,其中.在圖1中,δg(h(t))表示跟隨者g與領導者1 在二維XOY平面內相對距離,分別表示跟隨者g與領導者1 在OX軸和OY軸方向上的相對距離,h(t) 為調整上述相對距離的時變信息,例如當跟隨者繞領導者做旋轉運動時,h(t) 可表示旋轉半徑和旋轉角速度信息(見數值仿真部分).

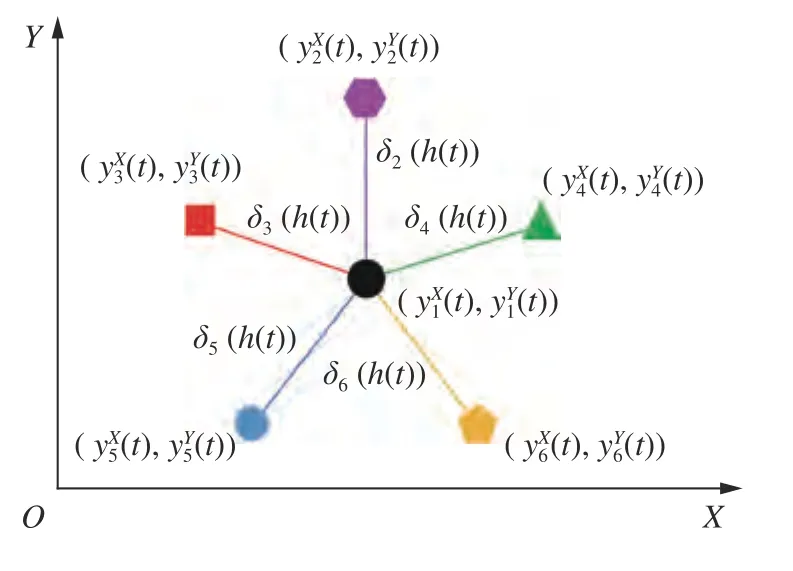
圖3 集群系統輸出時變編隊跟蹤示意圖Fig.3 The illustration of time-varying output formation tracking for swarm systems

引理 1[17].對于任意正定實對稱矩陣J1,J2∈Rn×n和任意向量a∈Rn,以下不等式關系成立:

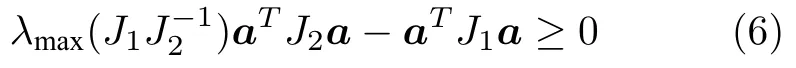
其中,λmax(J)表示矩陣J的最大特征值,下同.

引理 2[31].如果假設1 成立,式(2)中分塊矩陣的所有特征值均具有正實部.同時,存在正定對角矩陣使Eβ >0,記表示的最小特征值.

2 控制協議的設計

本節將給出控制協議的設計方法,考慮到集群系統中領導者存在已知或未知控制輸入,領導者和跟隨者存在未知擾動,有向通信拓撲存在切換等多種因素影響,且領導者的控制輸入在已知和未知兩種情況下控制協議的設計并不相同,因此對這兩種情況進行分開討論.

2.1 領導者存在已知輸入時控制協議的設計

當領導者的控制輸入是已知可設計時,通常對應領導者為合作目標的情況,則對領導者設計如下控制協議:

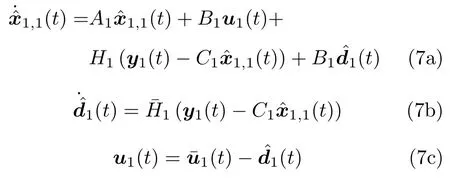
其中,式(7a)和(7b)為具有未知擾動時領導者對自身狀態的觀測器,式(7c)為基于該觀測器設計的控制器,表示領導者對自身狀態x1(t) 的估計值,表示領導者對其未知擾動d1(t) 的估計值,表示根據任務需求和領導者模型設計的控制輸入,以實現對領導者輸出軌跡的實時調控,H1、由下文中的算法1 確定.對跟隨者g ∈{2,3,···,1+N}設計如下控制協議:

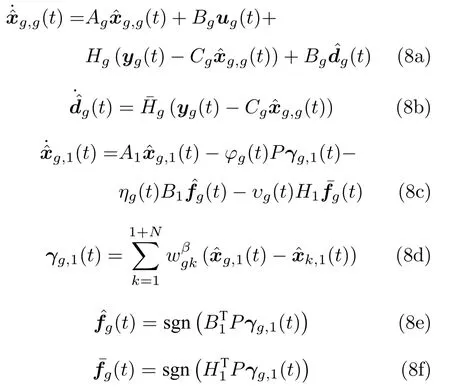
算法 1.通過下列步驟確定控制協議(7)和(8)中的待定參數:

步驟1.設計Rg、Sg和Ug使等式(3)和(4)成立.

步驟2.選取矩陣Hi和Hˉi使得矩陣Aˉi是Hurwitz 的,其中i=1,2,···,1+N.

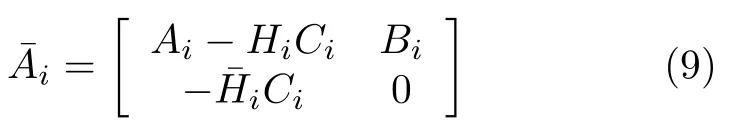
步驟3.選取θ >0,求下列Riccati 方程的正定實對稱解陣P.

其中,In1為n1階單位陣.由于 (A1,In1) 是可控的,所以存在唯一的解使得等式(10)成立[16].

步驟4.選取?g >0,ρg >0,?g >0,μ>0,σg >0,選取使得Ag+是Hurwitz 的,計算

步驟5.求下列Lyapunov 方程的正定實對稱解陣Qg.

其中,Ing為ng階單位陣.

步驟6.選取和滿足,且為非奇異矩陣.

證明.首先證明觀測器的收斂性.有關自身狀態觀測器(7a)和(7b)以及式(8a)和(8b)的收斂性證明過程詳見文獻[30],本文不再贅述.根據文獻[30]中的定理,定義dg(t),可知.現證明分布式觀測器(8c)～(8i)以及式(8j)和(8k)的收斂性.

構造Lyapunov 函數如下:

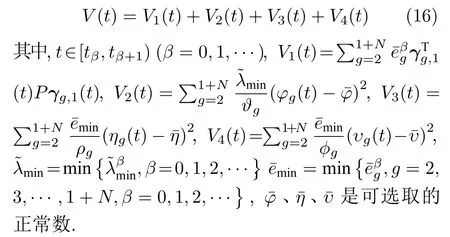
對V(t) 求導可得

令ζ(t)=V2(t)+V3(t)+V4(t),根據算法1 中的步驟3,可將式(25)進一步化為

更進一步由式(26)可得

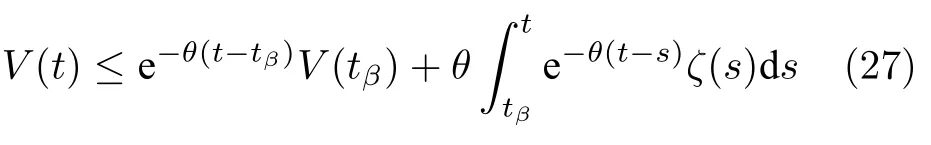
因為系統通信拓撲在t=tβ發生變化,如果β ≥1,則由引理1 可知

結合式(27)和(29)可得

同理根據式(26)可以推出

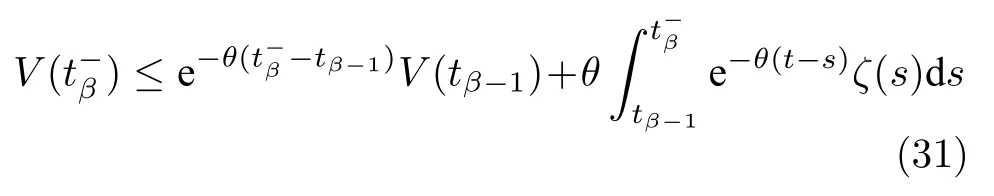
進一步根據遞歸方法可得

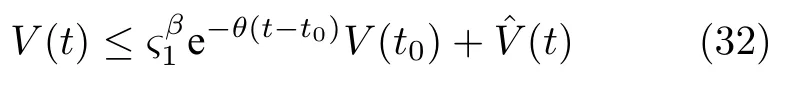
其中

討論以下兩種情況:

由t?t0=t?tβ+tβ?tβ?1+···+t1?t0≥t?tβ+βαmin且 ln?1?θαmin<0可得limt→∞V(t)≤ζ(t),矛盾,所以上述假設不成立.

進一步可得

接下來證明在控制器(8m)～(8q)的作用下異構集群系統能夠實現輸出時變編隊跟蹤.將控制器(8m)～(8q)代入式(1)中可得

由算法1 中的步驟6 和等式(12)可知

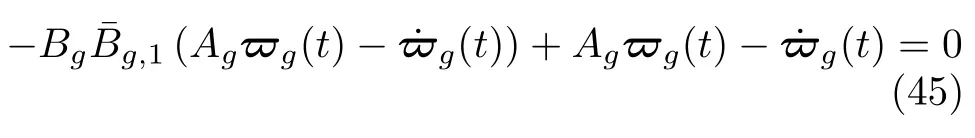
進而式(44)可化簡為

考慮如下Lyapunov 函數:

進而可得

2.2 領導者存在未知輸入時控制協議的設計

當領導者的控制輸入是未知不可設計時,通常對應領導者是非合作目標的情況,則只對跟隨者g ∈{2,3,···,1+N}設計如下控制協議:

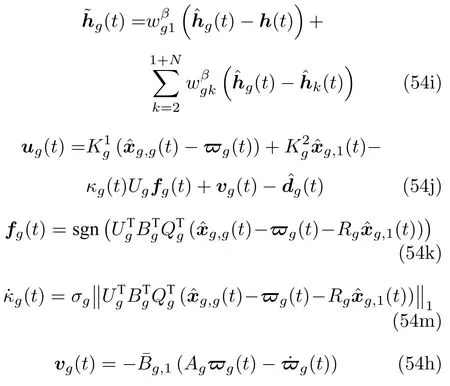
其中,各符號變量表示的含義保持不變.與控制協議(8)對比分析可知,式(54d)中利用的是領導者的全部狀態信息,而式(8d)中利用的是領導者根據輸出信息對其自身狀態信息的估計值,造成上述協議不同的原因是當領導者的控制輸入是未知不可設計時,無法通過領導者的輸出信息估計領導者的全部狀態信息,因此需要某個跟隨者能夠獲取領導者的全部狀態信息.相應的,式(54c)相比于式(8c),去掉對領導者自身狀態觀測器估計誤差的滑模補償項.需要說明的是,此時h(t) 為由某個能夠獲取領導者全部狀態信息的跟隨者調控的時變向量,控制協議(54)中的其他待定參數仍由算法1 確定.值得注意的是,當領導者的控制輸入是未知不可設計時,根據式(1)可知,此時領導者的未知輸入和未知擾動對跟隨者來說可整體看作領導者的未知輸入,因此可以得到下列定理.

定理2.對于任意給定的有界初始狀態,如果集群系統中的跟隨者采用控制協議(54),通信拓撲的最小駐留時間滿足 ln?1?θαmin<0 和ln?2?2μαmin<0,同時等式(12)成立,則異構集群系統能夠在有向拓撲切換條件下實現對存在未知輸入領導者的輸出時變編隊跟蹤.

由于控制協議(8)和(54)的主要不同體現在跟隨者對領導者狀態信息的觀測方法上,因此定理2 的證明過程類似定理1,此處略.由符號函數sgn(·)可知,控制協議(8)和(54)采用滑模控制方法來消除領導者的控制輸入、領導者的未知擾動以及跟隨者自身的未知擾動對集群系統的影響,因此抖振現象必然存在.現對控制協議(8)和(54)進行改進,參考文獻[16]提供的方法,分別用下列連續向量函數、cg(t) 代替控制協議(8) 和(54)中的、fg(t),進而使控制輸入產生較為平滑的連續性變化,能夠很好地抑制滑模的抖振現象.

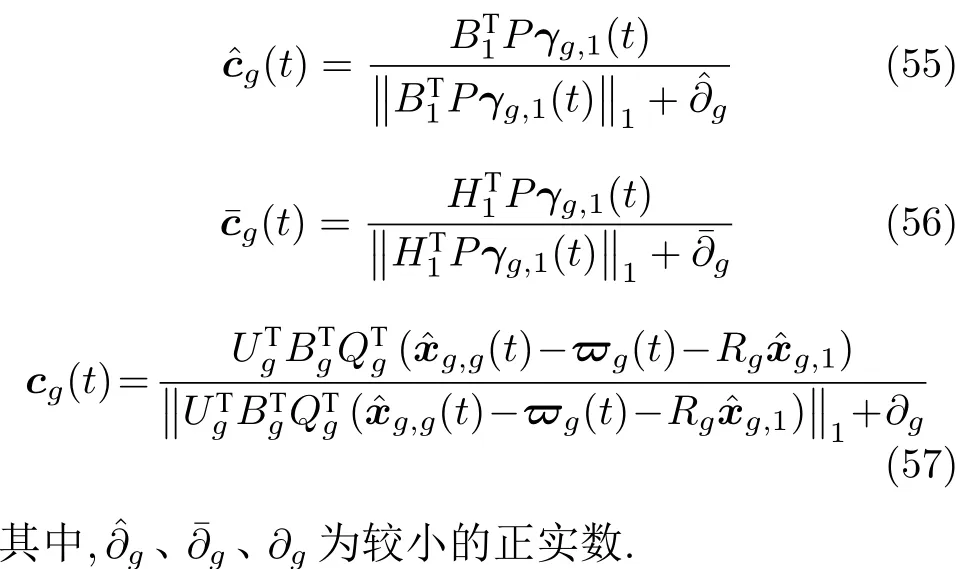
推論1.如果在控制協議(8) 中采用代替控制、fg(t),則異構集群系統對存在已知輸入領導者的輸出時變編隊跟蹤誤差(定義為‖yg(t)?zg(h(t))?y1(t)‖1)是一致最終有界的.

推論2.如果在控制協議(54) 中采用代替控制,則異構集群系統對存在未知輸入領導者的輸出時變編隊跟蹤誤差(定義為‖yg(t)?zg(h(t))?y1(t)‖1)是一致最終有界的.

考慮到篇幅原因,本文略去推論1 和推論2 的證明過程,感興趣的讀者可結合本文定理1 以及文獻[16]中定理2 進行推導證明.由推論1 和推論2可知 limt→∞‖yg(t)?zg(h(t))?y1(t)‖1≤Θg,Θg與、?g的選取有關.通過選取恰當的?g可使‖yg(t)?zg(h(t))?y1(t)‖1收斂到0 附近較小的有界區間內,以滿足實際應用需求.

由于控制協議(8)和(54)中均采用滑模控制方法,分析自適應律(8g)～(8i)、(8p)、(54f)、(54g)、(54m)可知,自適應增益φg(t) 、ηg(t) 、υg(t) 和κg(t)會一直緩慢地變大,因此可對自適應律(8g)～(8i)、(8p)、(54f)、(54g)、(54m)增加如下約束:

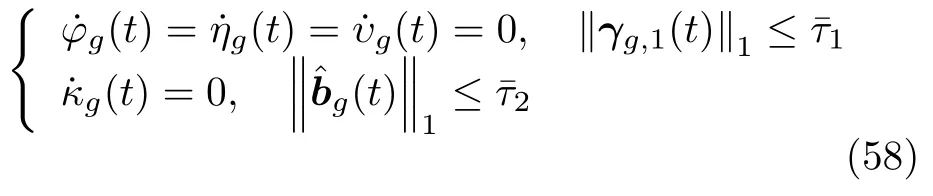
注4.由式(1)可知,本文研究的集群系統模型考慮比較簡單的匹配擾動,同時要求未知擾動滿足假設3,因此設計的自身狀態觀測器(7a)、(7b)、(8a)、(8b)以及(54a)、(54b)借鑒文獻[30]的研究成果,其結構相對簡單.如果模型考慮不匹配擾動或者觀測器匹配條件不滿足等更加復雜的條件時,對于未知擾動的假設條件也會發生相應的變化,可根據擾動形式的不同參考文獻[32?33]設計更加復雜的全維或降維觀測器.需要指出的是,當集群系統模型中擾動形式更加復雜時,除了對觀測器(7a)、(7b)、(8a)、(8b)以及(54a)、(54b)進行改進外,分布式觀測器(8c)～(8i)、(54c)～(54g)以及控制器(8m)～(8q)、(54j)～(54n)也要進行一定的改進,例如模型考慮不匹配擾動,即式(1)寫為

則分布式觀測器(8c)～(8i)、(54c)～(54g)以及控制器(8m)～(8q)、(54j)～(54n)中需要增加針對不匹配擾動Didi(t) 的滑模補償項,此處不作詳細論述,后續將進一步開展相關研究.

注5.本文提供的控制方法具有較強的普適性.首先本文研究的系統模型為異構模型,如果系統模型為同構模型,所有智能體具有相同的動力學模型,滿足Ai=A ∈Rn×n、Bi=B ∈Rn×m、Ci=C ∈Rp×n、可以驗證假設2 能夠成立,此時Rg=In、Ug=Im、Sg=0m×n,因此文獻[2?4],[6],[8],[11?14],[17],[20?21]研究的同構系統模型可以看作異構系統模型的特例.其次,本文研究的集群系統通信拓撲考慮有向拓撲切換的情況,而文獻[10?12]中考慮的無向拓撲固定、文獻[17]中考慮的無向拓撲切換以及文獻[4?9],[13],[15?16],[18?19],[21?22]中采用有向拓撲固定等情況均可以看作有向拓撲切換的特例.再次,本文研究的集群系統考慮考慮領導者存在已知或未知控制輸入,領導者和跟隨者均存在未知擾動的情況,而文獻[16],[19]中研究的領導者不存在輸入或領導者和跟隨者不存在擾動等情況都可以看作本文研究問題的特例.最后,本文對時變編隊函數設計了分布式觀測器,進而使時變編隊函數不再是全局信息,文獻[2?22]中的時變編隊函數均可看作是本文中時變編隊復合函數zg(h(t))的特例.

3 數值仿真

由于定理1 和定理2 的主要區別在于領導者的控制輸入是已知可設計的還是未知不可設計的,對應控制協議(8)和控制協議(54)的觀測器設計方法存在些許差異,在仿真層面上主要體現在領導者的運動軌跡是否可控,對于跟隨者是否能夠實現對領導者的輸出時變編隊跟蹤沒有明顯影響,考慮到篇幅原因,在驗證定理1 和定理2 時,對集群系統模型以及控制協議(8)和(54)的相同參數部分采用同樣的選取方法,并對控制協議(8)和(54)中自適應律(8g)～(8i)、(8p)、(54f)～(54g)、(54m)增加式(58)中的約束.假定集群系統含有7 個智能體,其中包括1 個領導者(對合作目標和非合作目標兩種情況分開討論)和6 個跟隨者,領導者標號為1,跟隨者標號為2～7,所有智能體采用如式(1)所示的異構模型,設定如下:

仿真中僅考慮XOY平面運動,集群系統在OX軸和OY軸方向上的控制可視為兩個獨立方向的解耦控制,所有智能體在OX軸和OY軸方向上的初始狀態在 (?8,8)中隨機選取,未知擾動在(0,1)中隨機選取,當領導者是合作目標時,領導者采用控制協議(7),其中=?0.1 cos(t),跟隨者采用控制協議(8),當領導者是非合作目標時,領導者的未知控制輸入假定為?2 cos(t),跟隨者采用控制協議(54),根據算法1以及式(58),控制協議(7)、(8)和(54)中的其他參數確定如下:

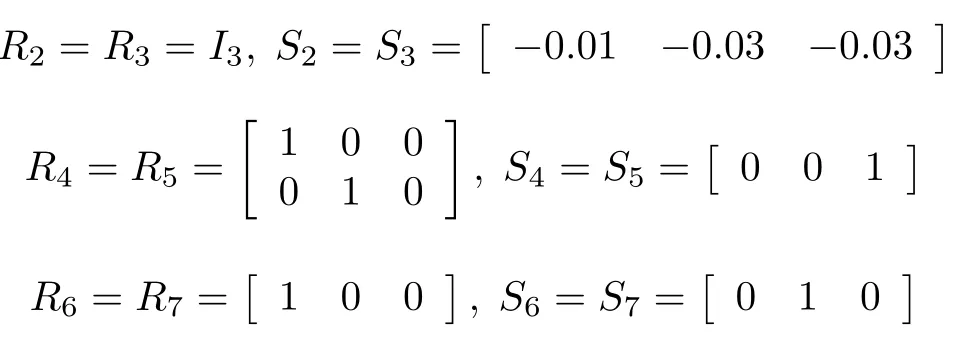
表征輸出時變編隊跟蹤隊形的復合函數及相關參數設計如下:

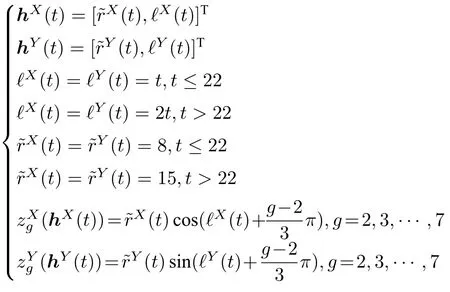
通過分析上述復合函數可知,仿真中期望跟隨者在以領導者為圓心、為半徑的圓弧上繞領導者運動,同時跟隨者之間保持固定的相對距離,領導者或與領導者直接通信的跟隨者能夠對圓弧半徑以及跟隨者繞領導者的轉動角速度的實時調控,當t∈[0,22) 時,圓弧半徑為8,轉動角速度為1 rad/s,當t∈[22,+∞) 時,圓弧半徑增大為15,轉動角速度增加為2 rad/s.圖4 給出了集群系統的通信拓撲關系,設定通信拓撲在駐留時間α=4s保持不變,到達切換時刻后在G1～G4之間切換.接下來對領導者是合作目標和非合作目標兩種情況的圖例進行分別說明.

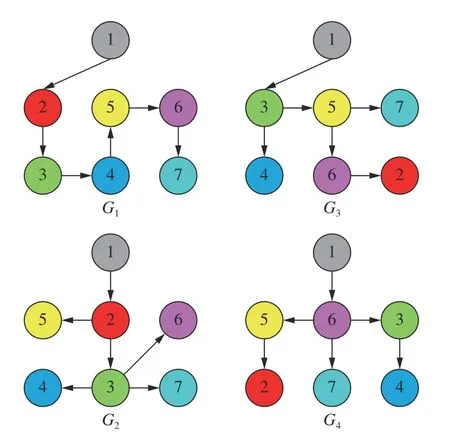
圖4 集群系統的通信拓撲關系Fig.4 The communication topologies of swarm systems

1)領導者是合作目標

圖5 給出了控制協議(7)和(8)中的觀測器的估計誤差(以所有智能體對自身狀態和領導者調控的時變向量的估計誤差為例),定義所有智能體對自身狀態估計誤差的二范數其中i=1,2,···,7,定義領導者調控的時變向量估計誤差的二范數其中g=2,3,···,7.從圖5中可以看出,控制協議(7)和(8)中的觀測器是收斂的.需要說明的是,圖5中在t=22 s時出現非連續的變化,原因是由于在t=22 s時編隊半徑瞬間增大且編隊轉動角速度瞬間增加.圖6 給出了跟隨者控制協議(8)中自適應增益(以和為例) 的變化曲線,其中g=2,3,···,7,由于對上述自適應增益增加了(58)中的約束,同時在t=22 s 時編隊半徑瞬間增大且編隊轉動角速度瞬間增加,因此圖6 中的自適應增益曲線存在部分不可微點.圖7 給出了跟隨者采用控制協議(8) 時在OX軸和OY軸方向上控制輸入的變化曲線,需要說明的是,控制輸入在t=22 s 時發生非連續變化,也是由于該時刻編隊半徑瞬間增大且編隊轉動角速度瞬間增加造成的.圖8 給出了集群系統在35s 內的輸出軌跡,并給出了部分時刻領導者和跟隨者的輸出分布.圖9給出了集群系統XOY平面內的輸出時變編隊跟蹤誤差,定義如下:

圖5 控制協議(7)和(8)中觀測器的估計誤差Fig.5 The estimation errors of observers in control protocol (7) and control protocol (8)

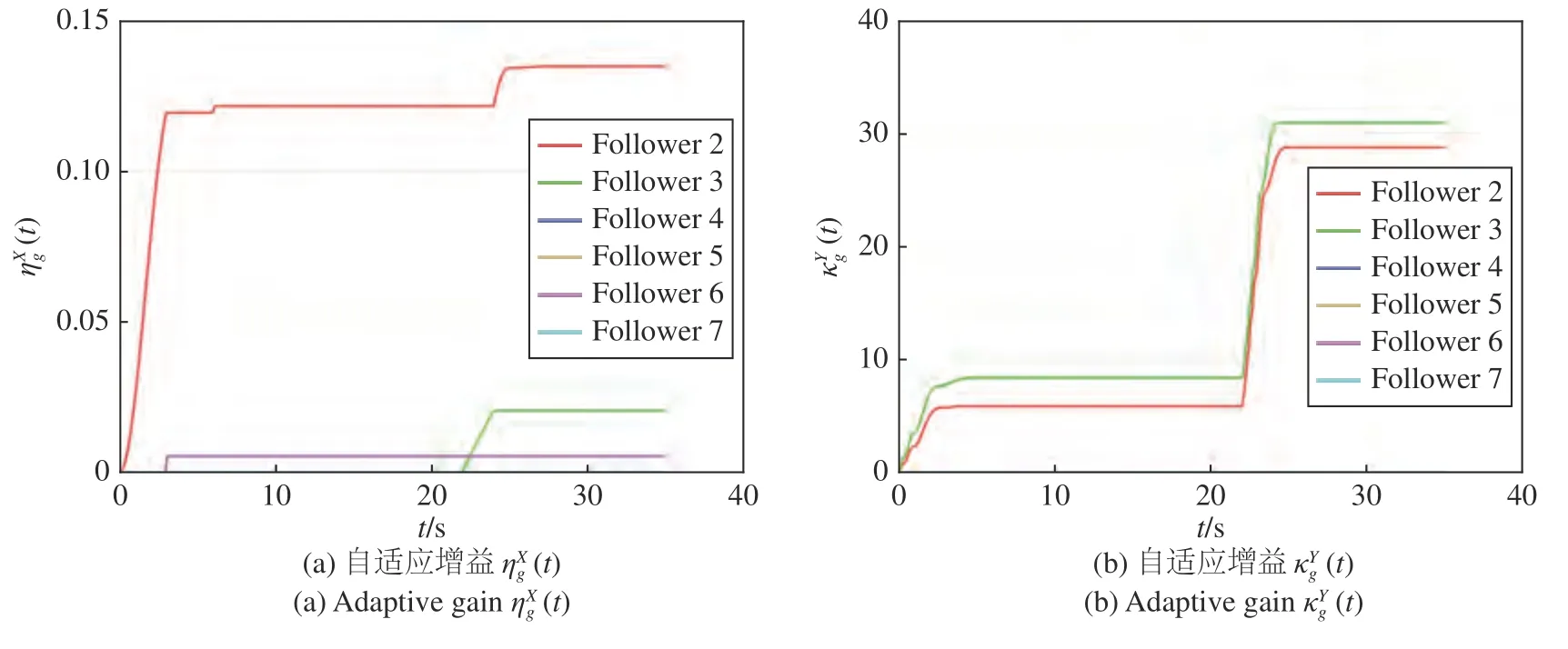
圖6 跟隨者控制協議(8)中的自適應增益變化曲線Fig.6 The varying curve of adaptive gains in followers′ control protocol (8)

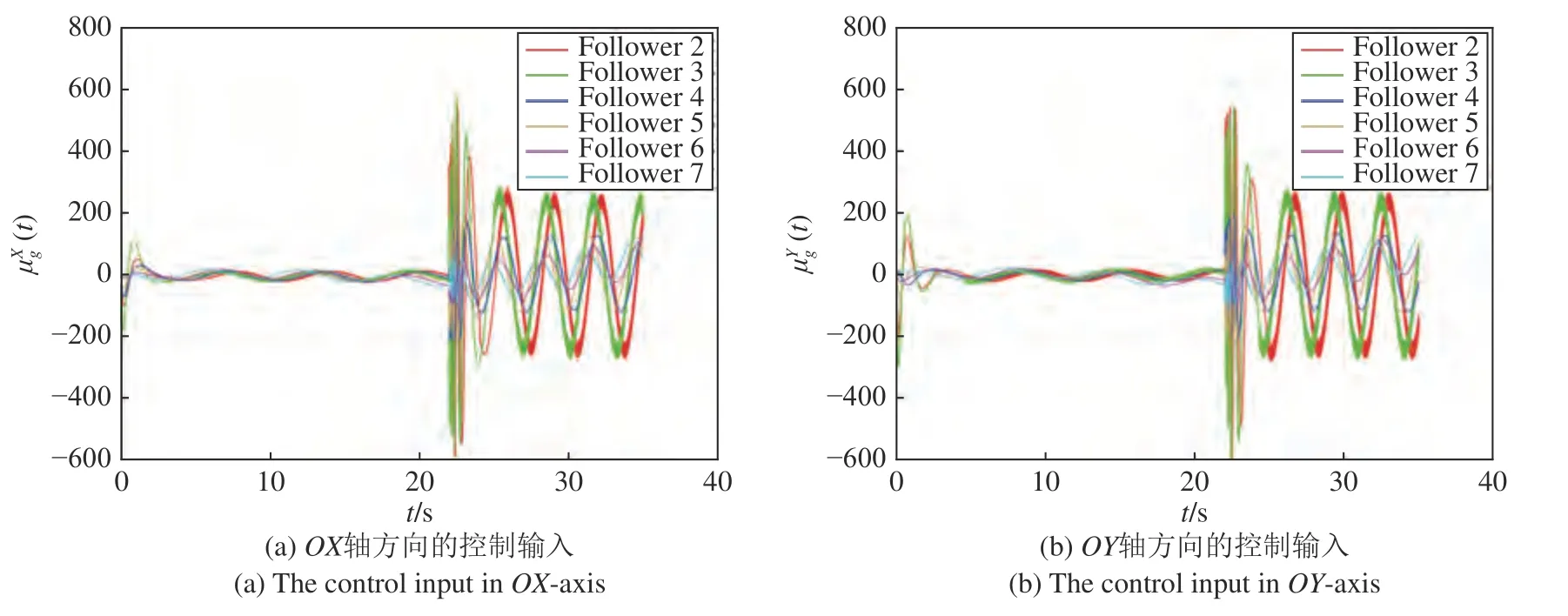
圖7 跟隨者控制協議(8)中的控制輸入變化曲線Fig.7 The varying curve of control input in followers′ control protocol (8)

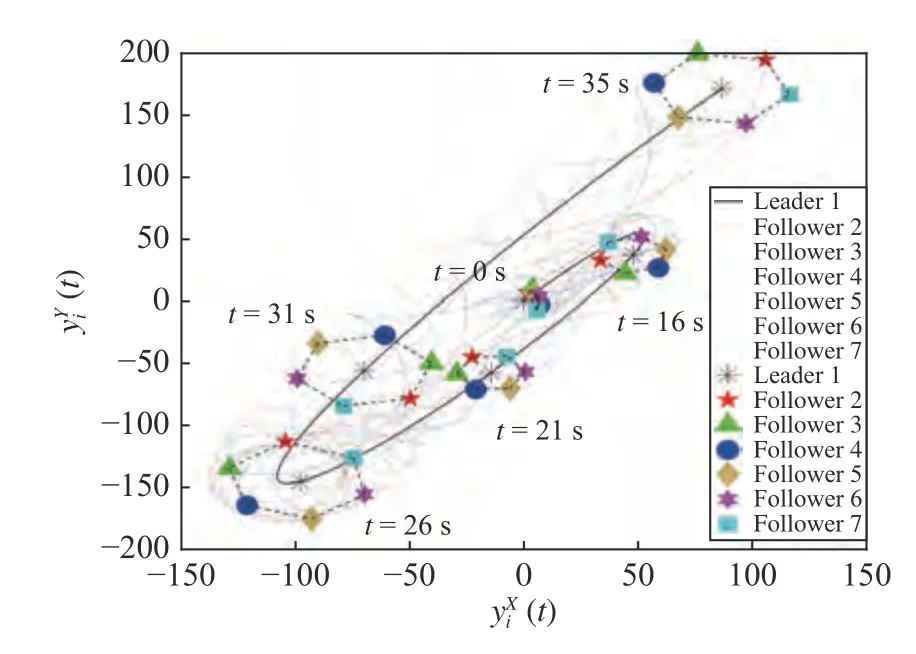
圖8 當領導者是合作目標時集群系統的輸出軌跡以及部分時刻的輸出信息Fig.8 The trajectory of output and the output information at partial moments associated with swarm systems when leader is cooperative target

其中,g=2,3,···,7.從圖9 中可以看出輸出時變編隊跟蹤誤差在編隊函數連續變化時快速收斂到0,在非連續變化瞬間會短暫增大(對應t=22 s 時編隊半徑瞬間增大且編隊轉動角速度增加),隨即快速收斂到0.

圖9 當領導者是合作目標時集群系統輸出時變編隊跟蹤誤差Fig.9 The error of time-varying output formation tracking related to swarm systems when leader is cooperative target

2)領導者是非合作目標

考慮到領導者是合作目標和非合作目標兩種情況下,仿真中集群系統參數選取的差異主要體現在領導者控制輸入的不同,為更直觀地進行仿真對比,當領導者是非合作目標時,仿真結果僅展示集群系統的輸出分布和編隊跟蹤誤差.圖10 給出了集群系統在35s 內的輸出軌跡,并給出了部分時刻領導者和跟隨者的輸出分布.與圖8 中領導者相對規律的軌跡相比,圖10 模擬了非合作領導者進行惡意機動的場景.圖11 給出了集群系統XOY平面內的輸出時變編隊跟蹤誤差 Υg.與圖9 類似,從圖11中可以看出輸出時變編隊跟蹤誤差在編隊函數連續變化時快速收斂到0,在非連續變化瞬間會短暫增大(對應t=22 s 時編隊半徑瞬間增大且編隊轉動角速度增加),隨即快速收斂到0.因此定理1 和定理 2 通過數值仿真得到了驗證.

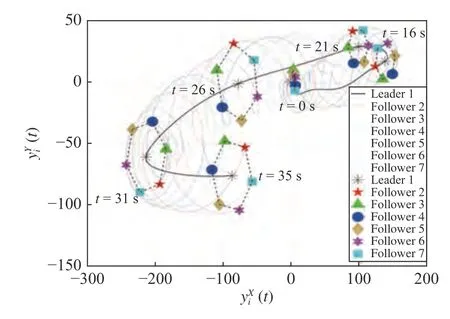
圖10 當領導者是非合作目標時集群系統的輸出軌跡以及部分時刻的輸出信息Fig.10 The trajectory of output and the output information at partial moments associated with swarm systems when leader is noncooperative target

圖11 當領導者是非合作目標時集群系統輸出時變編隊跟蹤誤差Fig.11 The error of time-varying output formation tracking related to swarm systems when leader is noncooperative target

4 結論

本文研究了高階異構集群系統輸出時變編隊跟蹤控制問題.基于觀測器理論、自適應控制理論、滑模控制理論等構造了分布式的控制協議,該控制協議分為觀測器和控制器兩個部分,觀測器包括對自身狀態的觀測器和跟隨者對領導者狀態的分布式觀測器,還包括針對時變編隊函數的分布式觀測器,基于上述觀測器構造了控制器,擺脫了對領導者的控制輸入上界值、與通信拓撲相關的拉普拉斯矩陣特征值以及時變編隊函數等全局信息的依賴,使本文的控制方法成為完全分布式的控制方法,因此本文提供的控制方法具有較高的理論研究和實際應用意義.未來會進一步將相關理論成果在無人機和無人車等實際物理系統上進行試驗驗證.