地球物理勘探中坐標轉換方法的探討

韓善朋

（吉林省有色金屬地質勘查局六〇五隊，吉林延吉133000）

1954北京坐標系和1980西安坐標系是20世紀我國建立的參心坐標系，隨著國民經濟的發展和科學技術的進步，各行各業都對坐標系統提出了更高的要求。因此我國應用現代測量技術手段建立了以地球質心為中心的CGCS2000坐標系。

CGCS2000坐標系于2008年7月1日開始啟用，日前自然資源部發布公告，宣布自2019年1月1日起，全面停止向社會提供1954北京坐標系和1980西安坐標系基礎測繪成果。

在地球物理勘探中，以往物探資料都是1954北京坐標系或1980西安坐標系，為了應用以往資料，坐標轉換及其正確性顯得尤為重要。

本文旨在探討在物探工作中常用的坐標轉換的方法原理及程序實現。

1 方法原理

坐標轉換分為二維坐標轉換和三維坐標轉換，二維坐標轉換是將平面坐標從一個坐標系統轉換到另一個坐標系統，需要4個轉換參數。三維坐標轉換不限制坐標形式可以是大地坐標也可以是平面坐標，一般需要7個轉換參數。為了保留地圖投影信息和坐標的通用性，一般采用三維坐標轉換。在地球物理勘查中坐標轉換流程如圖1所示。

圖1 坐標轉換流程

1.1 不同模型間空間直角坐標系的轉換

目前常用的空間直角坐標轉換模型有布爾沙模型和莫洛堅斯基模型。對于既有旋轉、縮放又有平移的兩個空間直角坐標系的坐標轉換，有7個轉換參數，相應的坐標轉換公式為：

式中：ΔX0、ΔY0、ΔZ0——3個平移參數；

m——尺度變化參數。

為了求得這7個轉換參數，至少需要3個公共點，當多于3個公共點時，可按做小二乘法求得7個參數的最或然值。

1.2 大地坐標與平面坐標間的轉換

在地球物理勘探中，為了方便計算，常采用平面坐標，將大地坐標轉換為平面坐標即地圖投影。在物探工作中最常用到高斯投影，詳查和勘探中常用3°分帶，概查和普查中常用6°分帶。

1.2.1 高斯正算

高斯正算是將大地坐標轉換為平面坐標，公式為：

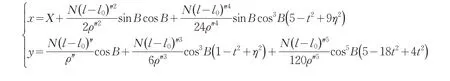
式中：x、y——平面坐標；

B、l——大地坐標；l0——中央子午線；

習主席指出，沒有網絡安全，就沒有國家安全。網絡安全關乎國計民生，更關乎戰爭勝負。未來戰爭，兵馬未動，信息先行。信息化戰爭條件下，網絡攻防行動更是貫穿整個戰爭的始末。新形勢下，省軍區系統在后備力量調整改革過程中，緊跟時代發展，挖掘地方信息科技潛力，組建民兵網絡信息分隊，在近幾年一些重大活動安保行動中發揮了重要作用。目前，民兵網軍這支新質新銳后備力量隊伍雖然已經初步建成，但是仍然面臨較多的問題和矛盾，需要進一步研究和規范。

X——自赤道起的子午線弧長；

N——卯酉圈曲率半徑。

1.2.2 高斯反算

高斯反算是將平面坐標轉換為大地坐標，公式為：

式中：Bf——底點緯度與橢球參數有關。

1.3 大地坐標與空間直角坐標間的轉換

大地坐標與空間直角坐標的轉換指的是在同一坐標下進行的。某點的空間直角坐標（X,Y,Z）和大地坐標（B,L,H）之間的轉換公式為：

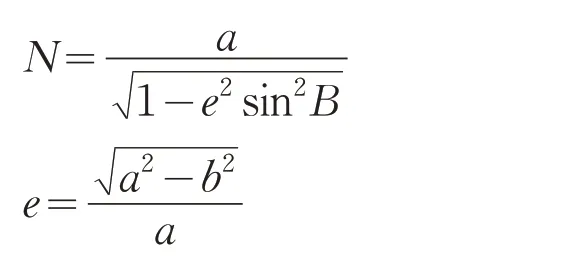
式中：N——卯酉圈半徑；

e——第一偏心率；

a、b——橢球的長半軸和短半軸。

2 程序設計

通過MATLAB編寫坐標轉換程序，程序主要分為轉換參數求解和坐標計算兩個部分。

利用1.1中的坐標轉換公式編寫計算模型參數代碼，利用此段代碼實現轉換參數的計算。

編寫高斯反算代碼，分為兩個函數，第一個函數［Bi,l］=GS_DD_1（a,e,x,y）采用迭代法求出底點緯度，第二個函數［B,L］=GS_DD_2（a,e,Bf,x,y）調用第一個函數進行高斯反算。利用此段程序實現平面直角坐標向大地坐標的轉換。

編寫代碼空間直角坐標和大地坐標的相互轉換。分別用函數［X,Y,Z］=DD_ZJ（B,L,H,a,e）和［B,L,H］=ZJ_DD（X,Y,Z,a,b,e）來實現。

編寫高斯正算代碼，分為兩個函數，第一個函數［X,l,t,l,N］=DD_GS_1（B,L,a,b）用來計算子午線弧長，第二個函數［x,y］=DD_GS_2（B,L,a,b）需要調用第一個文件進行高斯正算。利用此段程序實現大地坐標向平面直角坐標的轉換。

3 實例計算

選擇在吉林省延邊地區某物體工作中的坐標轉換為例，驗證以上原理和程序的正確性。工作中需要將北京54坐標系下的高斯平面坐標轉換為CGCS2000系統下高斯平面坐標。

共收集到工作區兩套坐標下的重合點5個，如表1所示，為了安全起見，本文僅顯示坐標整數位后三位。選擇均勻分布的1、4、5號公共點求取轉換參數。

表1 公共點對一覽表

將求得的轉換參數輸入到程序中，得到轉換模型。利用2號重合點和3號重合點對程序正確性和計算精度進行檢核。計算誤差如表2所示。

表2 計算誤差對比表

經檢驗，程序的計算精度在1m以下，滿足物探工作精度要求。

4 結論

通過對坐標轉換方法原理的研究和分析，利用MATLAB程序設計語言編寫坐標轉換程序，并且在實際物探工作中得到了應用，應用實例表明該程序方法原理正確，計算結果精度滿足現行規范要求。該程序的實現使得在物探工作中的坐標轉換問題得以解決，大大地提高了工作效率。