基于差分進化算法的不同濃度冰漿流動特性研究
邵佳棟,周文杰,郝 帥,許文柱,周延鎖
(1.杭州電子科技大學能量利用與自動化研究所,杭州 310018;2.天津大學機械工程學院,天津 300072)
0 引言
中國的乳制品加工正在從量產轉型為質產。為了減少乳品加工生產過程中的碳排放,提高乳制品質量,關鍵環節是冷卻。冷卻的目的是為了在高溫殺菌后迅速降溫以保證乳品的質量。對國內乳制品加工生產情況的調研發現[1],為了滿足乳制品冷卻需求,我國往往采用大型冷水機組來提供冷源。目前,集聚式冷水機組已經能夠滿足現階段乳制品加工日益增長的冷源需求,但是該方法存在不可忽視的缺點[2]:(1)冷卻速度慢且冷卻過程中溫度不穩定;(2)冷水機組頻繁開停機使其壽命減少的同時用電量增加;(3)所需電功率大,增加了電網負荷;(4)制冷系統自動化程度低,生產效率低。
冰漿由一定體積分數的冰和冷水組成,其相變潛熱較大,比冷水的蓄冷能力和制冷效果好。研究表明,冷水機組須增加80%~350%的流量才能達到與冰漿制冷系統相同的制冷效果[3]。同時,冰漿制冷系統中包括冰漿儲存裝置,該裝置能夠在夜間儲存流態冰供白天使用,節省用電成本。因此,目前在某些領域冰漿制冷系統正在逐步代替傳統的制冷裝置,本文通過研究不同體積分數冰漿的流動特性,為冰漿制冷系統設計提供參考意見。
1 典型冰漿制冷系統
圖1為一家奶酪加工廠冰漿制冷系統的示意圖。該廠每天生產9萬公斤奶酪。奶酪發酵劑冷卻和乳清蛋白濃縮、過濾等過程的冷卻負荷估計為每天2 546 kW·h。冷卻負荷峰值出現在上午7:00,此時干酪發酵劑須從85℃降溫到25.5℃,此過程需要265 kW的冷卻負荷。峰值負荷僅在白天出現,只有1 h,廠內其他冷卻需求使該時間內總峰值負荷達到396 kW,其余23 h中,總冷卻負荷在56~148 kW間變化,占峰值負荷的40%以下[4],如圖2所示。
為了降低負荷高峰,填補負荷低谷,使負荷曲線趨于平滑,安裝了一個冰漿制冷系統,該系統由一個功率為106 kW的冰漿發生器和24.6 m3的儲槽組成,能夠儲存763 kW·h的能量,如圖1和圖2所示。
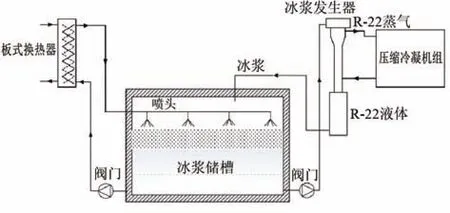
圖1 奶酪加工廠冰漿制冷系統示意圖Fig.1 A schematic of the cheese processing ice slurry plant
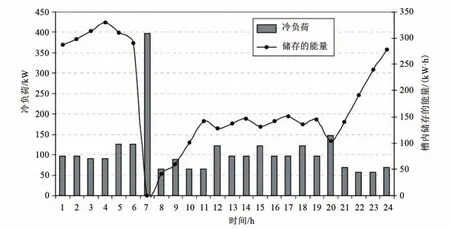
圖2 24 h冷卻負荷分布和儲槽中的能量曲線Fig.2 Load profile and storage tank capacity over a 24-hour period
冰漿制冷系統連續運行,用7%體積分數的丙二醇初始水溶液生成5%~10%體積分數的冰漿。生成的冰漿被泵送到儲槽,由于密度差異,冰晶和冰溶液分離并分別占據儲槽的上部和下部。一個大約為0℃的冷凍溶液從儲槽底部被泵送到換熱器,“溫暖”的溶液返回儲槽,并通過噴霧噴頭分布在冰晶層上。
冰漿制冷系統在不需要或需要較少冰漿時,冰漿發生器產生的冰漿被泵送到儲槽中備用;當有冷卻需求時,將冰漿從儲槽中泵出,通過管道運輸至冷卻區域。王子龍等[5]的研究發現,流動過程中,冰漿會摩擦管道內壁產生壓降,而壓降會對系統的熱容量和功耗造成影響,壓降越大,系統的熱容量越小,功耗越大。因此研究如何在滿足制冷需求的情況下產生盡可能小的壓降,對提高制冷效果和減少功耗具有重要意義。
2 冰漿湍流模型與算法
懸浮液在管內的流動分為三種模式:懸浮流、移動床和固定床,冰漿在管內的流動也分為這三種[6]。流動狀態取決于流體自身的特性,而流體的特性是多種參數相互影響的函數。當冰漿在管道中運輸時,由于其流動的復雜性,冰漿的可視化是困難的,其流型也難以控制。一些學者研究發現,可以通過轉換速度對冰漿的流動狀態進行分類:Wasp等[7]將從層流過渡到湍流的速度稱為“過渡速度”;Shook等[8]把冰漿顆粒層開始形成時的速度稱為“臨界沉積速度”。
以臨界沉積速度為特征,一些冰漿研究學者如Frei等[9]觀察到,當冰漿速度低于臨界沉積速度時,壓降增加,載流體(NaCl溶液)無法攜帶流體中的冰顆粒,這時容易造成冰堵。因此要選取大于臨界沉積速度的流速,使流體處于懸浮狀態。值得注意的是:當臨界沉積速度增加時,出現冰堵的可能性高。
由于冰漿在管內流動的復雜性,常常用經驗函數來計算其臨界沉積速度,常用的有[7]:
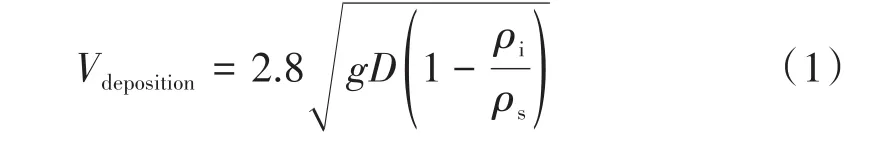
式中:g為重力加速度,9.8 m/s2;D為管道直徑,mm;ρi為冰密度,kg/m3;ρs為溶液密度,kg/m3;
按照式(1)計算,8%質量百分數的NaCl溶液在50 mm管徑下的臨界沉積速度約為0.7225 m/s。許多不同的實驗表明[10],冰漿在低的體積分數時表現為牛頓流體,在高的體積分數時則表現為非牛頓流體。對于等溫流動,溫度是恒定的,不考慮能量方程。這種流動的壓降可以用達西-魏斯巴赫公式(Darcy-Weisbach)計算:
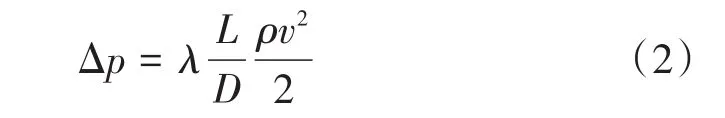
式中:λ為流體摩擦因子;L為管道長度,m;ρ為冰漿密度,kg/m3;v為冰漿的流速,m/s。Darcy-Weisbach公式充分反映了冰漿在管內的流動壓降。
λ可以用不同的流體模型來描述,其中,Sasaki等[11]提出的賓漢姆模型被眾多學者如Kauffeld等[12]采用。Marr等[13]認為冰漿是一種冪律膨脹流體。Snoek[14]更偏愛卡森模型。本文采用Reghem[15]提出的一種針對冰漿在換熱器中流動的半經驗公式:
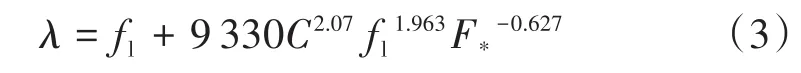
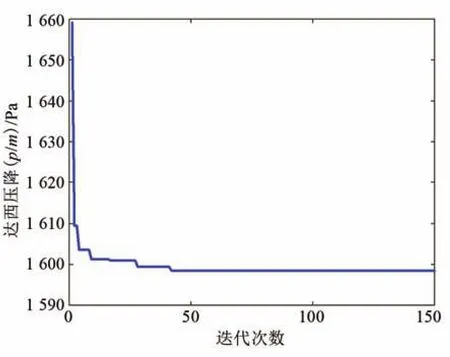
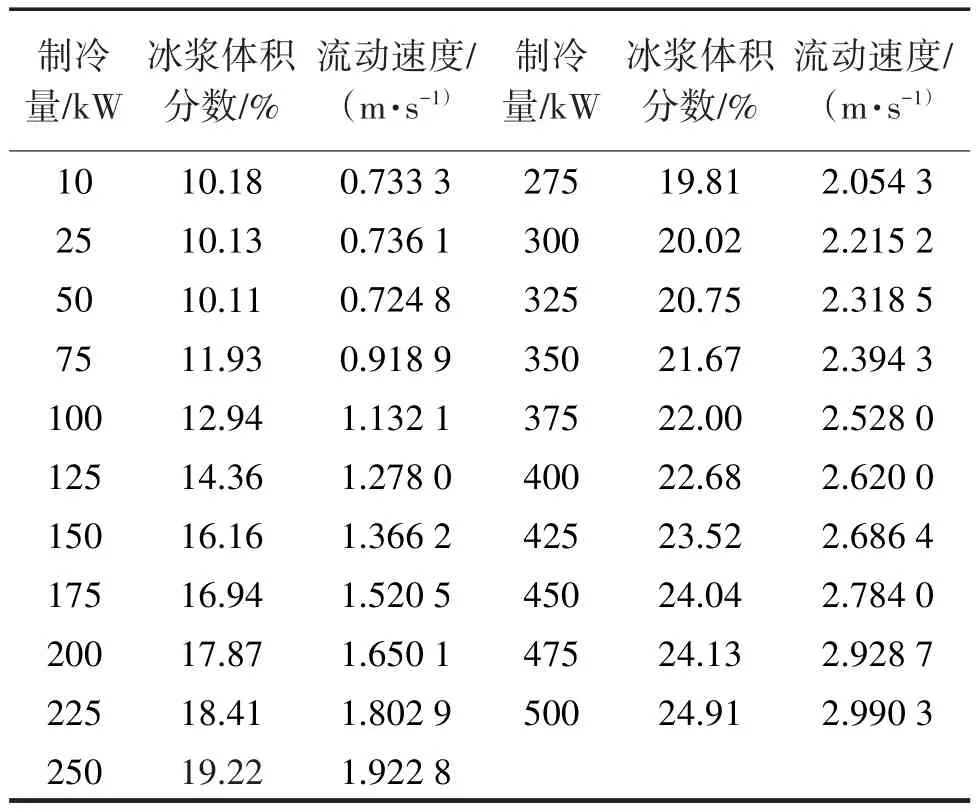
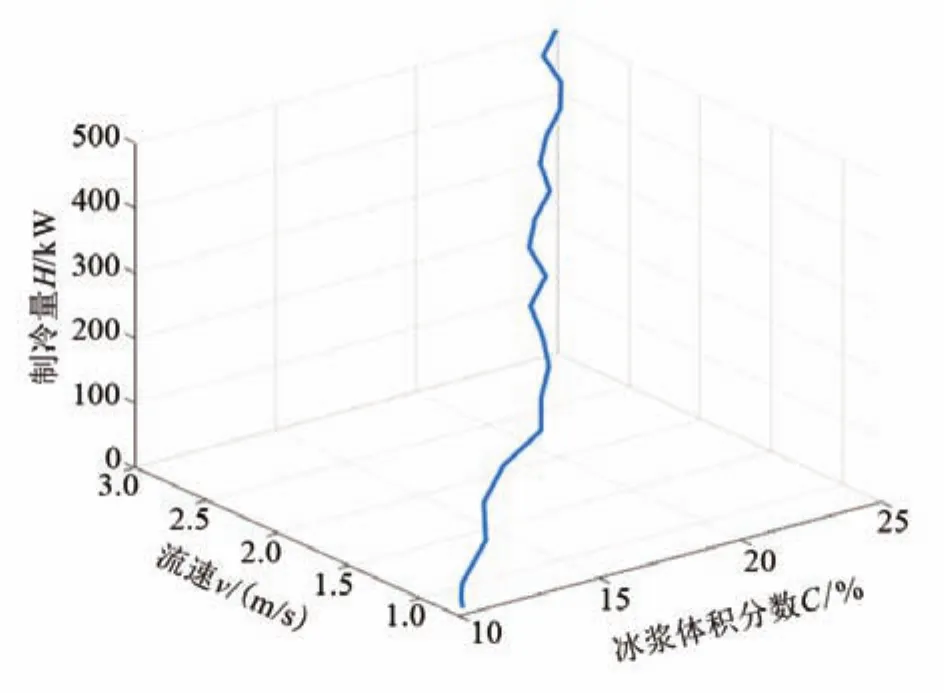
該半經驗公式的適用條件為流速:v<4 m/s,冰漿體積分數:10% fl是Blasius提出的單相流在管內流動的摩擦因子: F*是弗勞德數,其計算公式如下: 隨雷諾數Re不同,流體流動可分為層流和湍流[16]。對于冰漿制冷系統,為了保證生產過程的穩定與安全,須避免冰漿在管內的流動為移動床和固定床模式,防止冰堵現象出現對經濟生產造成損失,因此只考慮冰漿的湍流狀態。雷諾數的計算公式為: ηB為流體黏度,通常根據載液(冰漿)的濃度計算出懸浮液(固體顆粒分散于液體中的混合物)的有效黏度。已有許多不同的模型用于懸浮液黏度的測定,其中大多數實質上是愛因斯坦黏度方程的延伸[17]。本文采用托馬斯方程[18]計算流體黏度: 式中:ηL為溶液黏度;為保證冰漿在管內為湍流,選取雷諾數為0.64×104~0.42×105。 采用海水冰漿(NaCl)作為研究對象,由于NaCl溶液密度與冰密度相近,因此采用線性加全方法來獲得冰漿密度[19],公式如下: 根據式(8)作出圖3。 圖3 冰漿密度與冰漿體積分數和NaCl溶液密度的關系Fig.3 The relation between ice slurry density and ice concentration and NaCl solution density 從圖3可以看出,隨著冰漿體積分數的增加,冰漿密度減小。結合式(2)與式(3)~(8),給出冰漿體積分數、管徑與壓降的關系,如圖4所示;流速、管徑與壓降的關系,如圖5所示;冰漿體積分數、流速與壓降的關系,如圖6所示。 圖4 管內達西壓降與冰漿體積分數的關系Fig.4 The relationship between the flow pressure in the tube and the concentration of flow ice 從圖4可以看出,隨著冰濃度增大,管內達西壓降不斷增大。 從圖5可以看出,隨著流動速度增大,管內達西壓降也不斷增大。 圖5 管內達西壓降與流速的關系Fig.5 The relationship between the flow pressure and velocity in the tube 從圖6可以看出,同時考慮冰漿體積分數和流速時,隨著它們增大,管內達西壓降也增大。 圖6 管內達西壓降與冰漿體積分數和流速的關系Fig.6 The relationship between flow pressure and ice concentration and flow rate in tube 管道輸送能力可以由流體質量流量乘以補給線和返回線之間的焓變表示。冰漿在溫度(T)下的焓變ΔH可以寫成: 式中:Q為單位時間內的流量。 式中:t為時間,s;hice為冰的潛熱,335 kJ/kg。 確定了流量即可計算流體攜帶的冰的制冷能力。當確定了制冷所需的能量時,就能通過改變速度來調整管內的達西壓降。 冰漿是一種被用作熱載體和用來儲存能量的流體。冰漿系統的優化是對其具有產生溫差、傳熱和儲能部件的系統的優化。 冰漿流動過程優化由三個基本部分組成: (1)由Darcy-Weisbach方程獲得冰漿流動過程中壓降最小值; (2)獲得影響壓降最小化的冰漿體積分數和流速變化組合; (3)最終在滿足制冷量要求前提下獲得允許的冰漿體積分數和流速變化取值范圍。 本文采用差分進化算法(DE)[20]作為最優化算法。DE算法是從自然界生物的遺傳、變異、優勝劣汰的進化中感悟而發展的一門基于種群的搜索算法。算法由四部分組成:初始、交叉、變異和選擇。利用DE算法,產生可能的初始冰漿體積分數、流動速度組合,經過交叉、變異兩個操作篩選出滿足要求的組合,再進一步篩選,最終一步步逼近優化值,四個步驟的詳細過程和結果如下。 目標函數為Darcy-Weisbach方程,使達西壓降盡可能的小;變量選擇為冰漿體積分數和流動速度;約束條件為10%~30%的冰漿體積分數、0.722 5~3 m/s的流動速度以及滿足一定要求的制冷量。 (1)初始化種群,在DE中,種群由個體組成,每個個體可以表示為: 在初始化階段,確定最小邊界xmin和最大約束xmax,之后,每個個體被初始化,如式(12)所示。 式中:i,j為自變量;NP為種群規模,取50;CL為染色體長度,本次模擬中表示冰漿體積分數和流速兩個變量,取2;rand[NP,1]為產生一個NP行1列的矩陣;xmin和xmax為變量的最小值和最大值。 經過上述步驟,產生了一個初始種群X[x1,x2],其中x1為冰漿體積分數,x2為流動速度來儲存每一代的解。 (2)交叉 交叉操作是生成子個體的第一部分,每個子體的代表為: 按如下方式創建: CR表示交叉概率,0.1。例如,將X矩陣中的隨機兩組解“冰漿體積分數10%,流速1 m/s”與“冰漿體積分數20%,流速2 m/s”中冰漿體積分數或流速交換,變成“冰漿體積分數10%,流速2 m/s”與“冰漿體積分數20%,流速1 m/s”,就能使數據選取更具隨機性。 (3)變異 DE有三個主要的操作符:交叉、變異和選擇。變異操作符是生成子個體的第二部分,也是DE算法中最重要的一部分。此處Ur1,G,Ur2,G,Ur3,G代表從交叉過后的種群中隨機選擇的三個個體,通過變異算子突變個體與父個體結合生成新的子個體[21]。 每個突變個體如下所示: F為變異概率,0.4;r1,r2,r3在種群中隨機選取且r1,r2,r3和i互不相等。為保證交叉變異后產生的新個體仍然滿足約束要求,根據式(9)為冰漿優化加入制冷量前提,為個體插入邊界約束條件后對新個體再次篩選,若不滿足約束,則返回過程(2)重新進行流程。得到V矩陣,其中儲存了經過一輪篩選過后既滿足變量取值范圍又滿足制冷量需要的冰漿體積分數和流速組合。 (4)選擇 選擇運算符是DE過程的最后一個操作符,這個運算符選擇一些將成為下一代種群的個體,其基礎是比較父個體和子個體的適合度值。如果父個體的適應度值大于子個體的適應度值,則在下一代種群中父個體繼續存在,子個體被淘汰。否則,父個體被替換為子個體。下一代個體的選擇: 將變異得到的子代代入Darcy-Weisbach方程得到相對應的壓降值,通過比較保留每代中壓降值小的個體組成新的父代種群進行下一次迭代篩選。隨著進化代數的增加,種群必然收斂于最優解,即得到滿足制冷前提的最優冰漿體積分數和流速配比。 圖7為DE算法流程圖。 圖7 DE算法流程圖Fig.7 DE algorithm flow chart 圖8是制冷量為250 kW時的尋優結果,在19.22%的冰漿體積分數和1.922 8 m/s的流速下可以既滿足制冷前提,又對管道有最小的壓力,表1、圖9為對不同制冷前提冰漿流動的數值模擬。 圖8 管內達西壓降隨迭代次數增加的尋優結果Fig.8 Optimization results of flow pressure drop in pipe with the increase of iteration times 表1 不同制冷需求下的冰漿體積分數和流動速度配比Tab.1 Ice slurry concentration and flow velocity ratio for different refrigeration requirements 圖9 制冷量隨流速與冰漿體積分數變化的尋優結果Fig.9 Optimization results of cooling capacity with flow rate and ice depth 結合表1和圖9可以看出,在低制冷量需求時,冰漿體積分數和流動速度的組合差別不大;隨著制冷量增加,(1)冰漿體積分數和流速的增加率保持穩定;(2)冰漿體積分數的增加比小于流速的增加比,這反映出冰漿體積分數對壓降的影響大于流速。 本文以海水冰漿為研究對象,采用Darcy-Weisbach方程與DE算法,得到了幾組在管徑50mm、8% NaCl溶液、不同制冷量下的冰漿體積分數和流速配比,該結果可在一定程度上減小冰堵現象的發生、減少系統功耗和提高制冷效果。通過模擬發現,當所需制冷量為250 kW時最佳冰漿體積分數為19.22%且流速為1.922 8 m/s,此時既能滿足制冷要求又能減少系統功耗,提高制冷效果。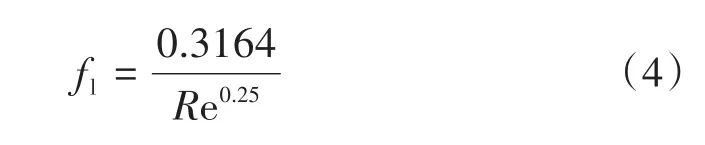
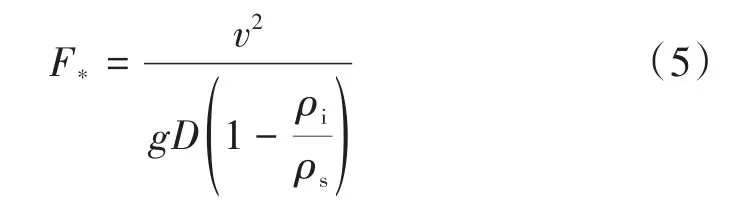

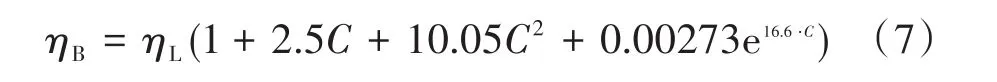
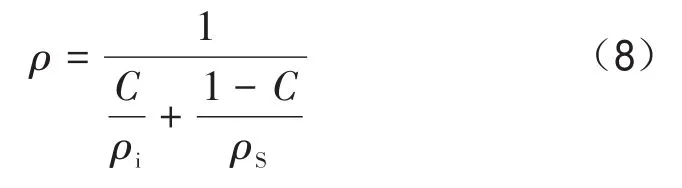
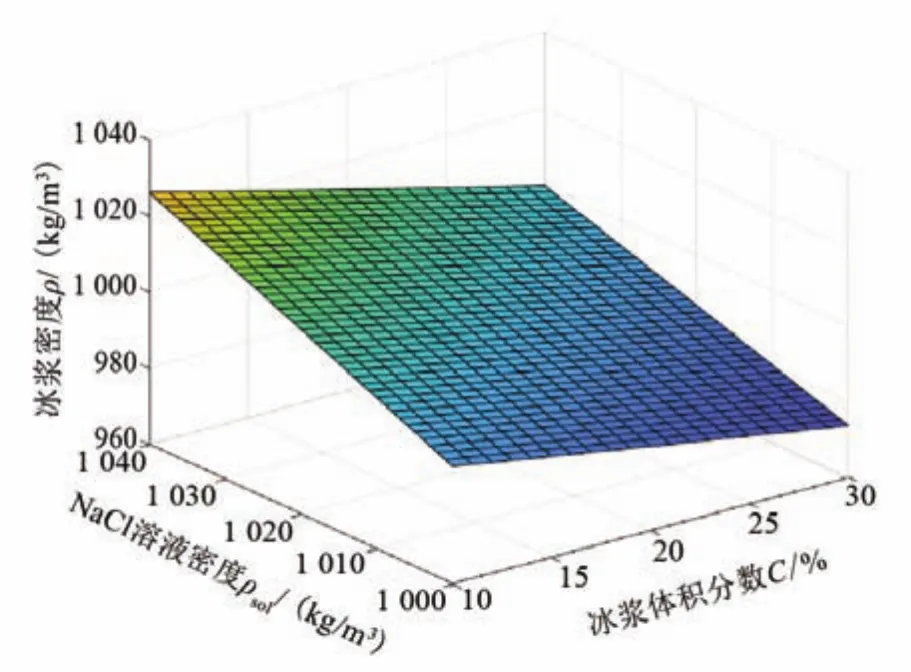
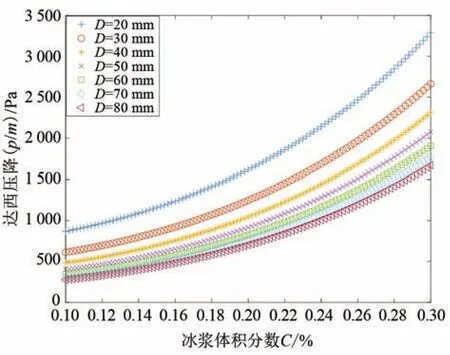

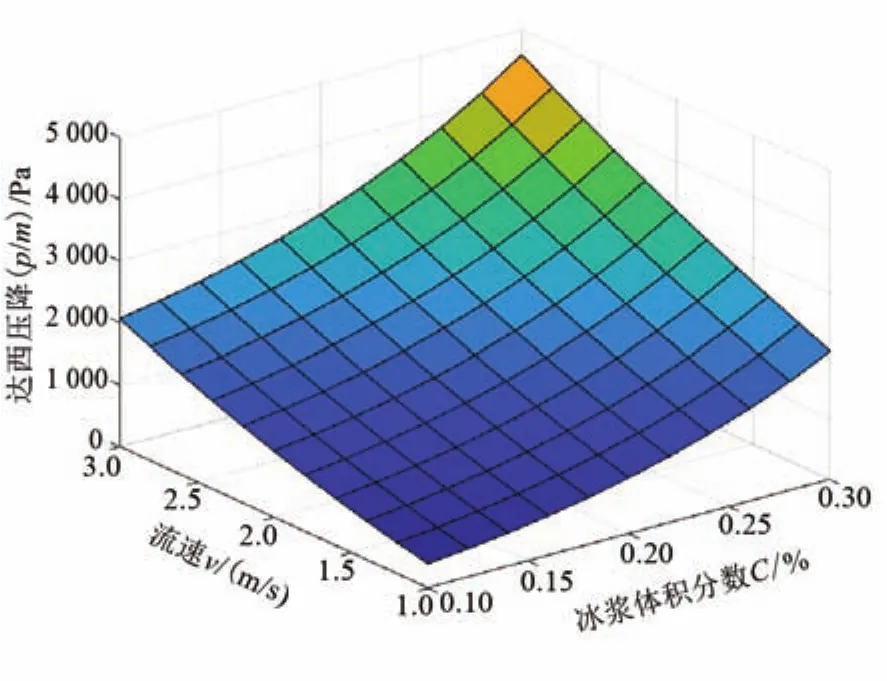





3 數據處理與分析
4 結論

