液氮供給系統液擊特性仿真研究

張 偉，王 柳，黃清妙，陳萬華，高 榮，陳建業，謝軍龍

（1.中國空氣動力研究與發展中心，四川 綿陽 621000；2.國防科技大學 空天科學學院，長沙 410073；3.華中科技大學 能源與動力工程學院，武漢 430074）

0 引言

管路系統中，由于某種原因導致流體流速劇烈變化，例如閥門關閉過快，流體流速驟變，使得流體內部壓力急劇變化的現象，稱為液擊（Liquid hammer）[1]。管道內發生液擊現象時，其最高壓力可達額定工作壓力的數倍甚至上百倍，管道以及管道上的閥門等附件承受巨大應力，可能會因此破損甚至斷裂，威脅系統的安全運行，液擊現象一直是管路系統研究中的熱點問題之一。低溫液體管路系統廣泛存在于航天和超導領域的低溫貯運系統中[2]，液氮是其中最為常見的低溫液體。液氮供給系統也是低溫風洞的核心系統之一，通過它向洞體內噴射液氮實現洞體降溫和低溫持續運行[3]。在機械切削加工領域中，用液氮作為冷卻介質可以強化冷卻刀具與加工區域，改善被加工材料的切削加工性、延長刀具壽命、提高工件的加工精度和表面質量[4-6]；利用液氮相變吸熱，可以使病變組織溫度迅速降低，應用于美容和各種惡性腫瘤的治療等[7-8]；利用液氮氣化絕熱膨脹產生動力的液氮汽車是當前環保汽車的一大發展趨勢[9-10]。上述應用的實現都有賴于液氮管路系統來輸運液氮。然而，液氮飽和溫度低，潛熱較小的特性，使其極易因漏熱、空化等作用而氣化，在管網內形成低溫流體氣液兩相流。液氮等低溫流體與常溫流體氣液兩相流和單相流產生的液擊現象有較大區別，研究液氮供給系統的液擊現象具有重要意義。

液擊現象研究多針對輸水工程和液化天然氣的裝卸船過程，主要圍繞液擊壓力、液擊波速影響因素和抑制措施展開。付鍇等[11]針對水管網中的液擊現象，利用Flowmaster進行了模型的搭建和仿真分析，分析了液擊現象對下游設備的影響，得到了發生液擊現象時管內壓力的變化情況。LNG的裝卸船過程具有歷時短、流量大、壓頭高（液體或液柱的兩點之間的高度差，m）等特點，易發生液擊現象[12]。韓旭等[13]利用特征線法對LNG卸船管道系統進行了模型的建立，計算了液擊壓力最大壓升，結果與文獻[14]中的實驗數據吻合良好，但其計算模型沒有考慮實驗過程中軟管對壓力波的衰減作用。液擊研究中涉及到多相流的相對偏少。李艷等[15]針對深海采礦時垂直輸送管道的液擊現象，基于AMESim模型，分析了管長、管徑以及顆粒濃度對水擊壓力和液體流速的影響，指出隨著固體顆粒濃度的增加，液擊壓力峰值相應增加，但流速下降。低溫推進劑的加注過程存在著盲支管填充和豎直管道的間歇泉（由于氣泡上升導致液體被間斷擠出管路的現象）等不穩定過程。劉海飛等[16]通過實驗，誘發了液氮填充盲支管液擊現象，發現當盲支管處于完全冷卻時，液氮從主管路到盲支管的填充過程導致了液擊現象的發生，管路系統的背壓越大，液擊壓力峰值越大，對系統的破壞性越強。

國內外研究者研究液擊現象時主要針對水工質，對于液氮等低溫流體的研究較少。此外，對間歇泉的研究雖然進行了氣液兩相流分析，但都是基于單管展開，復雜管網系統中的液擊現象仍有待研究。本文將以液氮為工質，采用AMESim仿真平臺，針對實際管網中發生的液擊現象開展研究。

1 液氮供給系統建模

1.1 液氮供給系統簡介

圖1為0.3 m低溫風洞的液氮供給系統（以下簡稱為LNS系統）原理圖[17]。該系統的功能是向噴嘴端輸送壓力穩定可控且調節迅速的液氮。LNS系統由液氮儲罐、柱塞泵、液氮緩沖罐、調節閥（PCV1801～1802、1804～1808）、流量計、壓力傳感器、電磁閥、真空絕熱連接管路以及固定有20個噴嘴的噴射排架組成。系統中布置有4個壓力傳感器和1個流量計。4個壓力傳感器分別監測主管路壓力、噴前壓力（調節閥閥后壓力）、總壓以及回流背壓，流量計監測20個噴嘴的噴射流量總和。通過啟閉噴嘴的數量和調節噴嘴噴射壓差實現精確控制噴嘴端的液氮噴射流量。可以看出，液氮儲罐-柱塞泵-緩沖罐-PCV1804～1807-電磁閥及噴嘴為主干路。此外，設有PCV1801-1802回流支路，目的是通過回流的形式，穩定主管路壓力，為主路噴射壓力和液氮流量調節提供前提條件。噴射排架前安裝有排氣調節閥PCV1808，以便在噴嘴全部關閉的情況下供給管路一定的液氮流量，保證系統正常運行，4個壓力傳感器 P1、P2、P3、P4分別監測主管路壓力p1、噴前壓力p2（調節閥閥后壓力）、總壓p3以及回流背壓p4。

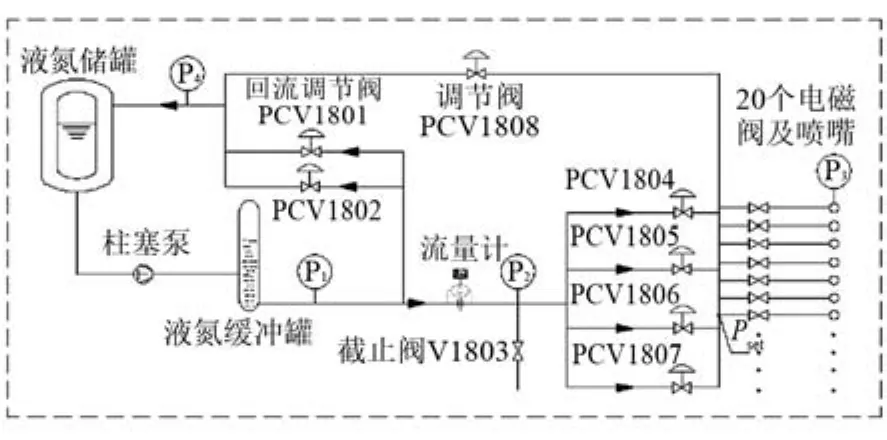
圖1 液氮供給系統原理圖Fig.1 Schematic of LN2 supplying system

1.2 液氮供給系統建模

在AMESim軟件平臺中，對LNS系統的液氮柱塞泵、緩沖罐、調節閥、噴嘴等關鍵部件進行單獨建模。對于管路系統，取流體微元dx，建立其運動微分方程如式（1）：

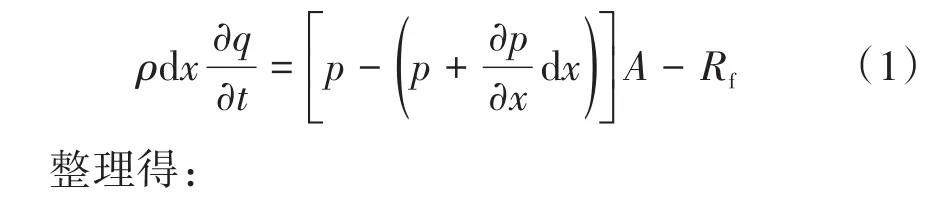
式中：ρ為流體密度，kg/m3；p為壓力，Pa；q為流量，m3/s；t為時間，s；A為流體管路的橫截面積，m2；Rf為與頻率相關的流體摩擦阻力，N；Ke為流體的表觀體積彈性模量，Pa；Ky為流體的體積彈性模量，Pa；D為管道外徑，m；b為管壁厚度，m；E為管材的彈性模量，Pa；ν為管材的泊松比。

通常采用流量系數來評價調節閥的通流能力：

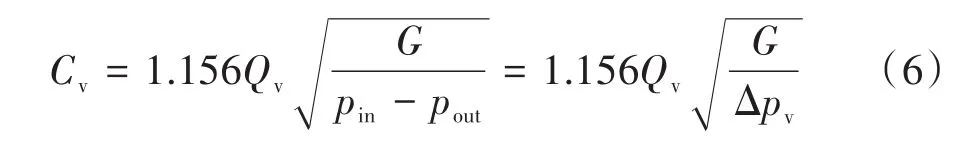
式中：Qv為流量，m3/h；G為比重（以水為參照，即水的比重1）；pin和pout分別為進口和出口壓力，Pa；?pv為閥門前后壓差，Pa。在此基礎上搭建了液氮供給系統的整體模型，對液氮供給系統進行仿真研究，系統仿真模型如圖2所示。

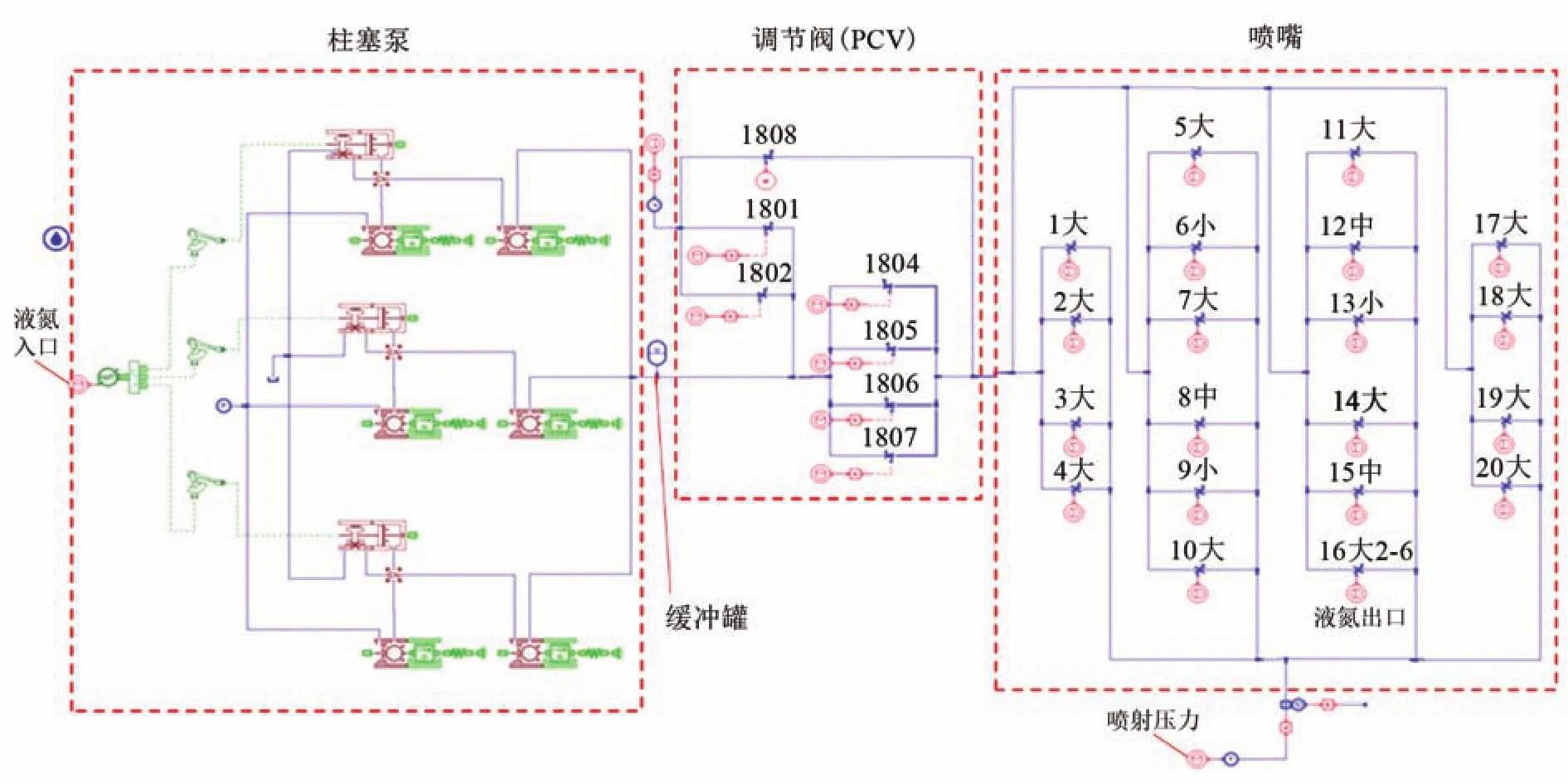
圖2 液氮供給系統仿真模型圖Fig.2 Simulation model diagram of LN2 supplying system

1.3 液氮供給系統仿真驗證

為驗證液氮供給系統液擊仿真模型的準確性，針對某次86.2 s的液擊實驗數據進行了分析。實驗過程中，在保持主管路壓力相對穩定的條件下，通過改變20個噴嘴的開閉實現了液擊。因此將噴嘴動作，柱塞泵轉速（520 r/min），調節閥后背壓和噴嘴出口背壓的實驗數據作為仿真模型的輸入條件。近似取液氮儲罐中0.44 MPa下飽和狀態液氮的物性。20個噴嘴動作如圖3所示，圖中每個噴嘴僅有兩個狀態值0和1，0表示噴嘴關閉，1表示打開。實驗過程中，有10個噴嘴保持常閉狀態，在剩余10個有啟閉動作的噴嘴中，噴嘴3、5、7、10、11、14、19為大流量噴嘴，噴嘴8、12為中流量噴嘴，噴嘴3為小流量噴嘴。三種噴嘴的工作參數如表1所列。調節閥PCV1808和噴嘴出口背壓如圖4所示。

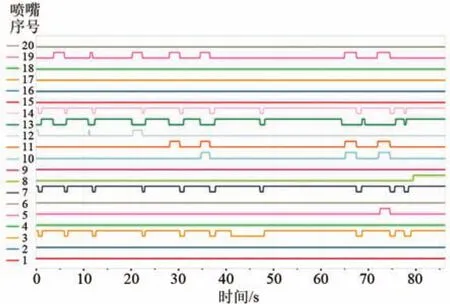
圖3 噴嘴動作示意圖Fig.3 Sketch of the action of the nozzles

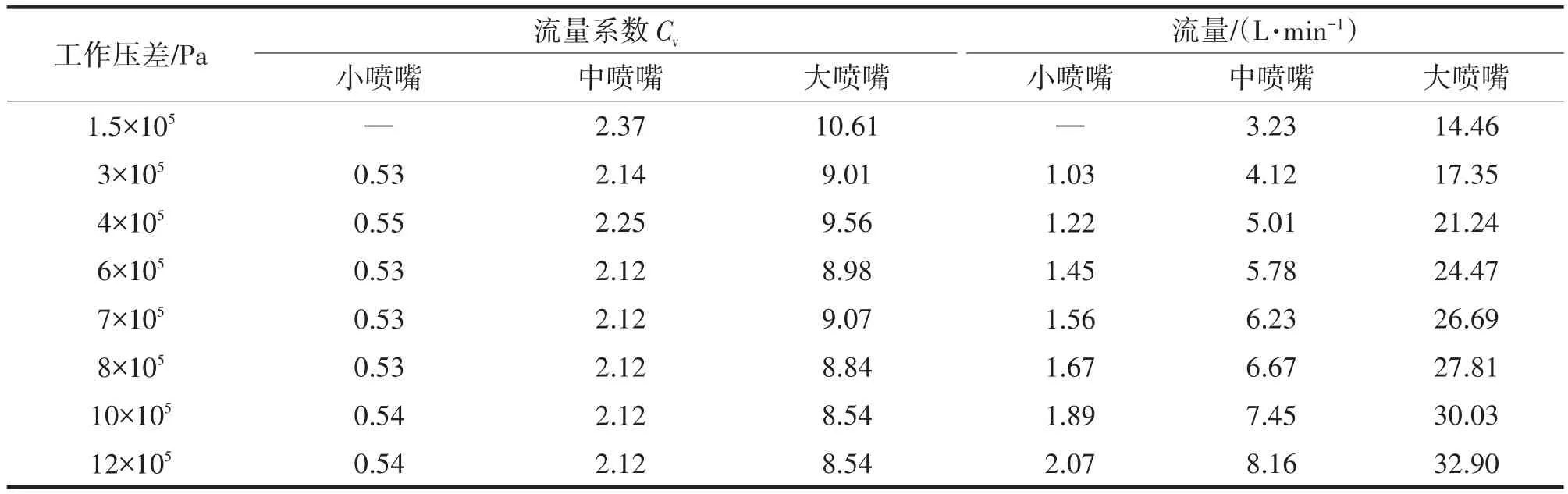
表1 不同壓差下噴嘴的工作參數Tab.1 Working parameters of the nozzles with various pressure difference

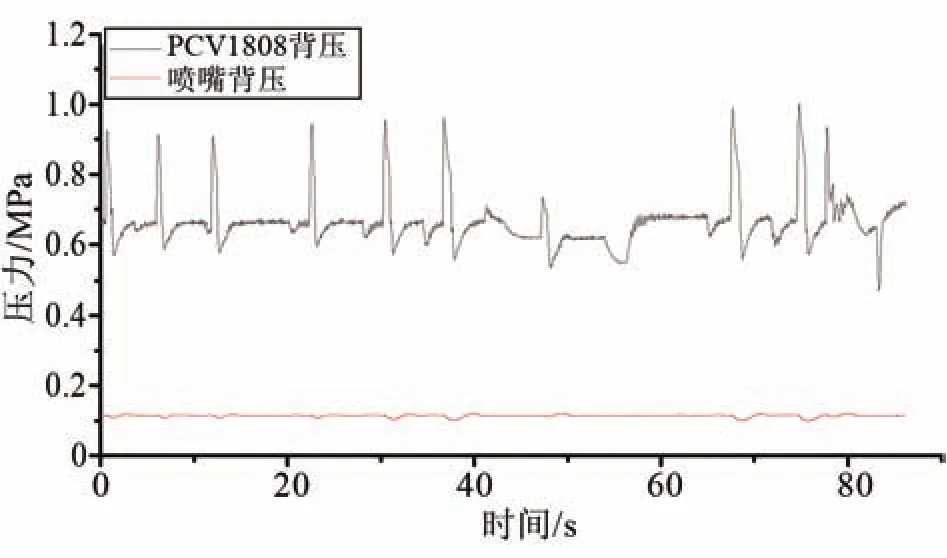
圖4 輸入壓力變化曲線Fig.4 Variation of inlet pressures

圖5和圖6分別為噴射流量和噴前壓力模擬值與實驗值對比圖。從圖中可以看出，隨著噴嘴的連續開閉，噴前壓力和回流背壓呈現出急劇上升又迅速回落的現象，其中噴前壓力可在瞬間達到2.4 MPa的峰值，又迅速回落至1.2 MPa左右。模擬值與實驗值吻合良好，平均誤差不超過2%，準確地描繪了因噴嘴連續啟閉而造成的噴射流量與噴前壓力的“陡升陡降”現象。但是與模擬值相比，噴前壓力實驗測量值存在高頻幅值衰減，如圖6虛線放大框所示。

1102 Down-regulation of grainyhead-like protein 2 promotes drug resistance of tumor cell to gefitinib by inducing epithelialmesenchymal transformation

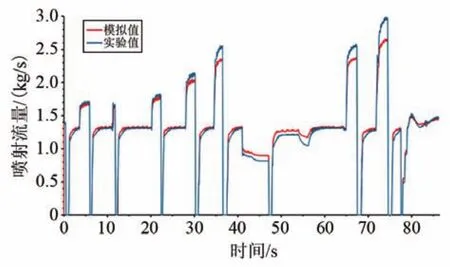
圖5 噴射流量模擬值與實驗值對比Fig.5 Comparison of jet flow rates between experiments and simulations

圖6 噴前壓力模擬值與實驗值對比Fig.6 Comparison of pressures before the nozzles between experiments and simulations

2 液擊現象的影響因素研究

在等徑直管中，當閥門突然關閉時，會造成關閥液擊，流體的動能轉換為壓勢能，最大壓力prmax為：

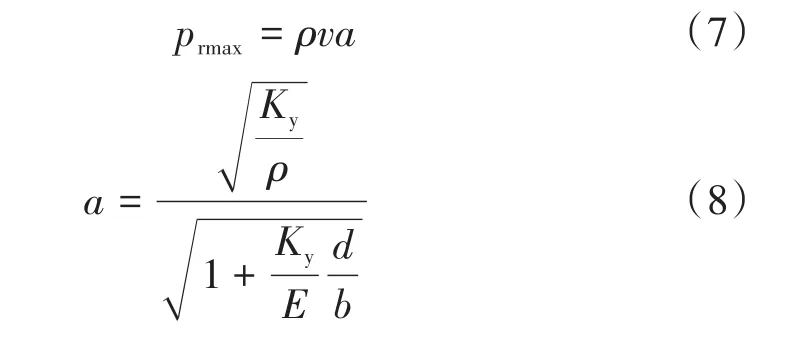
式中：v為穩流時（液擊前）流體的平均流速，m/s；a為流體中壓力波的傳播速度（波速），m/s；d為管道內徑，m。當閥門突然開啟時，會造成開閥液擊，出現的最大壓力pdmax為：

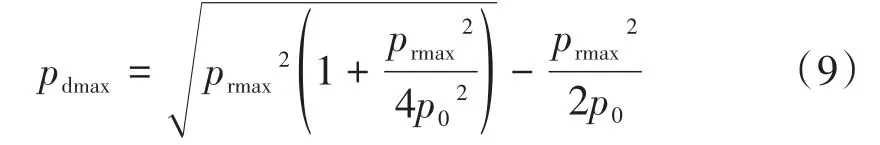
式中：p0為穩流時（液擊前）管道內的工作壓力，Pa。

可見，影響液擊現象的因素較多[18-20]，主要表現在流體物性、管道材料以及系統結構等方面。本節從流體物性和氣液兩相角度研究液氮密度、黏度、體積彈性模量以及含氣率對液擊現象的影響。對于本系統而言，液擊現象是由噴嘴的驟然關閉而致，仿真計算均以32～40 s的時域為研究對象。

2.1 密度對液擊現象的影響

為了研究密度對液擊現象的影響，設定了一組密度值做對比研究，其余物性均與液氮相同。根據實驗中液氮的狀態，取狀態點（100 K，2.6 MPa）下的密度值700 kg/m3進行研究，幾種高密度物質的密度分別設置為1 000、1 300、1 600 kg/m3。

36.5 s末噴嘴3、7、10、11、14、19驟然關閉，歷時0.1 s，此時所有的噴嘴均處于關閉狀態。由于噴嘴的驟然關閉，液氮供給系統形成液擊。當噴嘴突然關閉時，流體在慣性的作用下繼續向噴嘴端流動，直至流速為0，根據伯努利方程，液體的動能轉變為靜壓能，壓力達到液擊壓力的峰值，如圖7中a段所示；此時流體為不穩定狀態，噴嘴近端較噴嘴遠端的流體壓縮程度大，壓力更高，在不平衡的受力下，管內流體由靜止開始向上游流動，流速在數值上表現為負值，如圖8所示。管內流體從被壓縮狀態逐漸恢復，壓力也逐漸降低，直至流體從被壓縮狀態完全恢復為正常狀態，如圖7中b段所示；由于慣性，流體繼續向上游流動，而噴嘴端沒有流體補充，流速變為零，導致壓力也降低，產生減壓波，如圖7中c段所示，該過程中液體不可避免地發生氣化，以此遏制壓力進一步降低；因此，管內流體由靜止狀態又開始向噴嘴端流動，壓力也逐漸回升，如圖7中d段所示。由上述分析可知，當發生液擊現象時，液擊壓力與密度呈正相關關系，具有相同的波形，而速度與密度呈負相關關系。

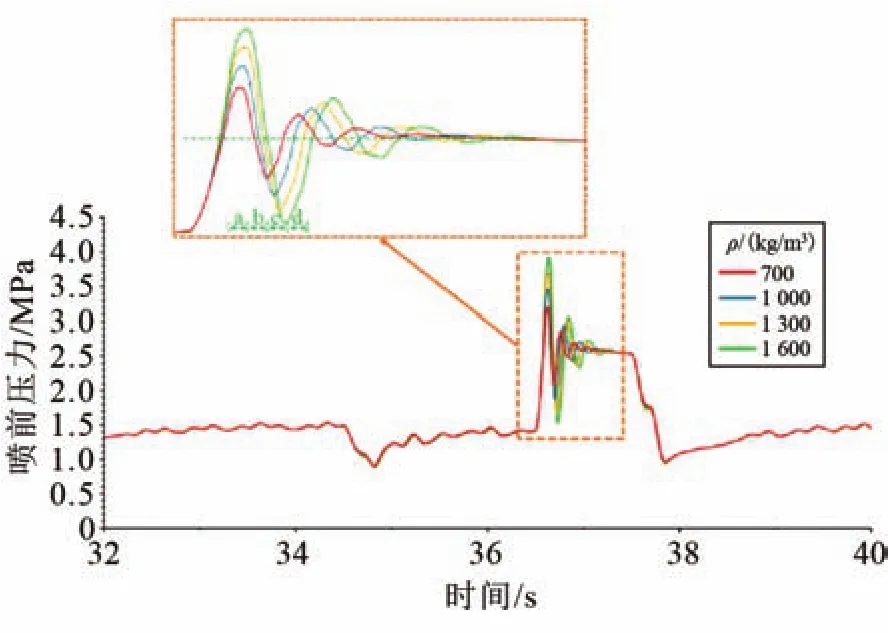
圖7 不同密度下液擊前后噴前壓力曲線Fig.7 Pressure before the nozzles with various densities

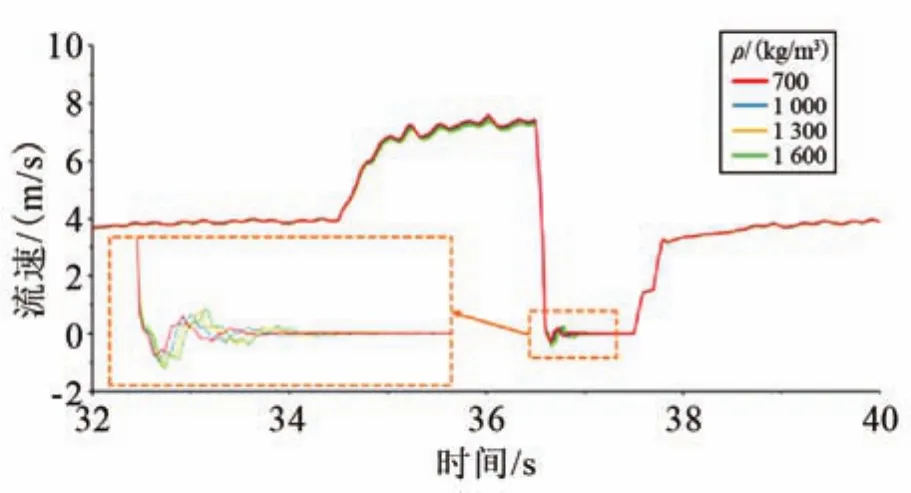
圖8 不同密度下液擊前后流速曲線Fig.8 Velocity with various densities during liquid hammer

當密度從1 600 kg/m3變化到700 kg/m3時，達到液擊壓力峰值的耗時從0.14 s變化到了0.12 s，而液擊壓力峰值從3.93 MPa變化到了3.2 MPa。雖然用各種液擊理論[21-22]計算出的液擊波速、液擊壓力峰值修正形式略有不同，但整體上為液擊波速，液擊壓差?p∝ (a,ρ)，這就解釋了流體密度越小，液擊波速越大、液擊壓力峰值越小的原因。

2.2 體積彈性模量對液擊現象的影響

圖9～10分別為不同體積彈性模量下的液擊壓力和流速對比圖。可以看出，體積彈性模量越小，液擊波速越小，液擊壓力達到峰值的耗時越長。

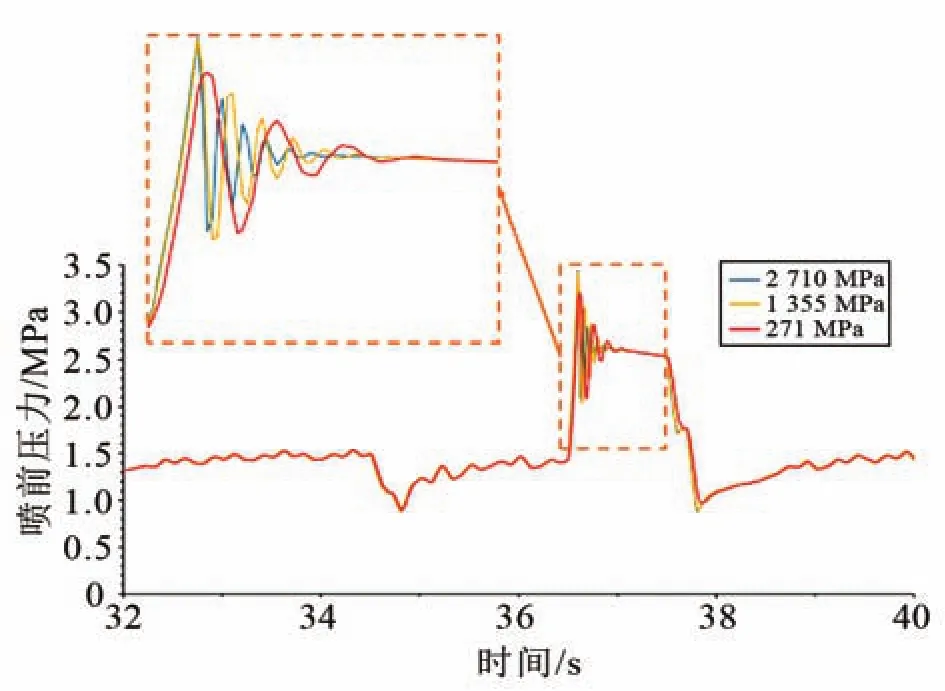
圖9 不同體積彈性模量下流體液擊前后噴前壓力對比Fig.9 Comparison of pressures before the nozzles with vari‐ous bulk modulus of elasticityduring liquid hammer

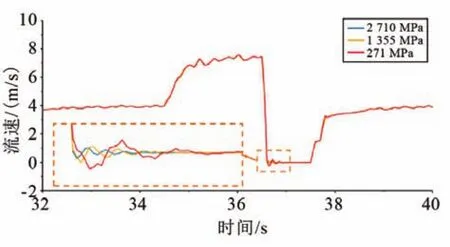
圖10 不同體積彈性模量下流體液擊前后流速對比圖Fig.10 Comparison of pressures before the nozzles with vari‐ous bulk modulus of elasticityduring liquid hammer

由于液擊壓變?p∝(a,ρ)，故而體積彈性模量越小，液擊壓力峰值越小。當體積彈性模量從2 710 MPa變化為271 MPa時，液擊壓力峰值從3.45 MPa變化為3.2 MPa，耗時從0.1 s變化為0.12 s。由此可知，液擊工況下的流速變化是由流體的慣性和可壓縮性導致的，流體的體積彈性模量越小，其可壓縮性越大，液擊工況下的流速波動越大。

2.3 黏度對液擊現象的影響

液氮的動力黏度為7.4×10-5Pa·s，約是常溫水的1/6，可能會導致液氮的液擊現象與水擊現象有著較大差別。圖11～12探究了不同黏度下的液擊壓力與流速對比圖。由圖可知，液擊工況下，流體的黏度越小，噴前壓力峰值越高，噴前壓力與流速波動越劇烈，液擊現象越顯著。當黏度增大到1 Pa·s時，噴前壓力與流速過渡平穩，已經觀察不到液擊現象；同樣可以看出，非液擊工況下的噴前壓力與流速隨著黏度的增大也逐漸減小，這是因為黏度越大，其流動摩擦阻力越大，相應的摩擦損失越大。液氮的黏度遠小于水，所以相同條件下，液氮的液擊壓力高于水，液擊更加劇烈。

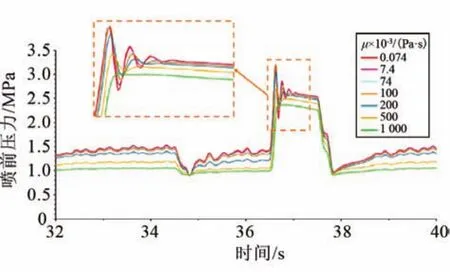
圖11 不同黏度下液擊前后噴前壓力對比Fig.11 Comparison of pressures before the nozzles with various viscositiesduring liquid hammer

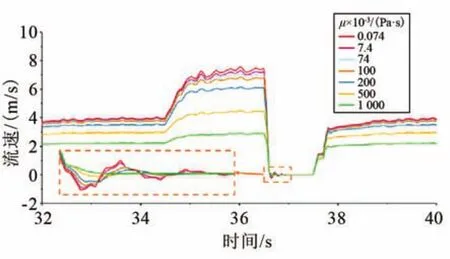
圖12 不同黏度下液擊前后液體流速對比Fig.12 Comparison of velocities with various viscosities during liquid hammer

2.4 含氣率對液擊現象的影響

對于氣液兩相流均相流模型，混合流體的密度ρ可以表示為：

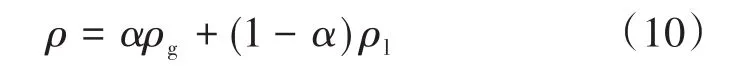
式中：α為含氣率（氣相體積分數）；ρg和ρl分別為氣相和液相的密度，kg/m3；混合流體的應力σ和應變ε有如下關系式：

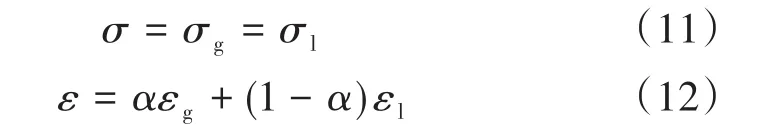
式中：σg和σl分別為氣相和液相的應力；εg和εl分別為氣相和液相的應變。流體的體積彈性模量Ky與流體的應力σ和應變ε的關系可以表示為：

式中：Kg與Kl分別為氣相和液相的體積彈性模量。由式（10）～（13）可得，對于氣液均相流模型，Ky可表示為[18]：

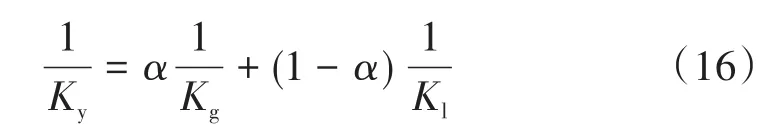
參考McAdams方法[23]，混合流體的兩相黏度μ可以表示為：

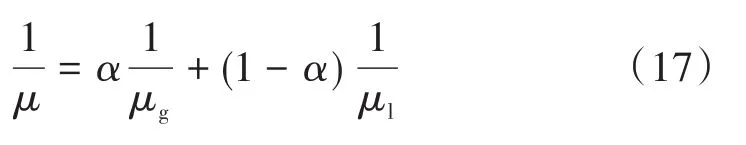
式中：μg和μl分別為氣相與液相黏度。

為探究含氣率的影響，對含氣率分別為0%、1%、2%、5%和10%液體的液擊現象進行研究。由式（8）可知，隨含氣率的增加，液擊波速急劇下降，不同含氣率下的密度、體積彈性模量、動力黏度和液擊波速對比如表2所列。

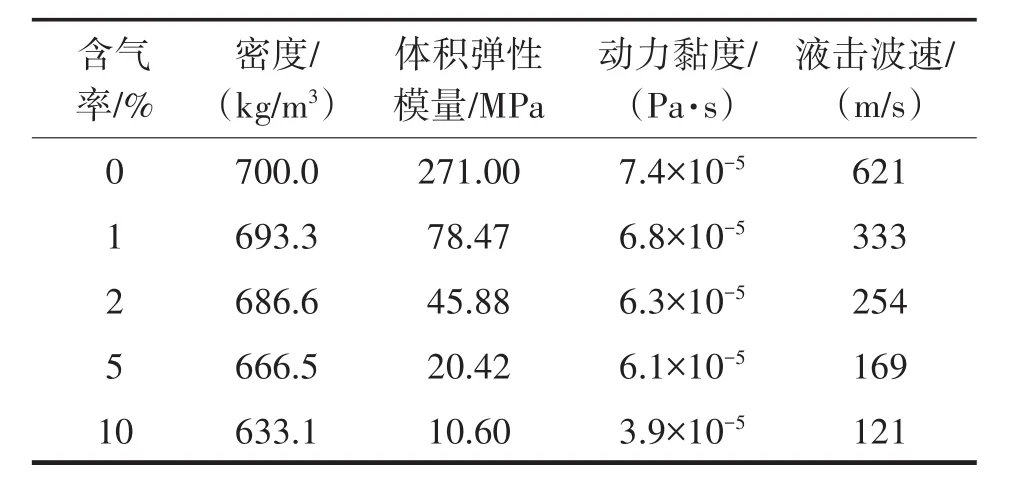
表2 不同含氣率下各參數對比Tab.2 Comparison of parameters with various void fraction

圖13為不同含氣率下的噴前壓力對比圖。隨含氣率的增加，液擊壓力峰值逐漸降低，當含氣率為5%和10%時，已觀察不到明顯液擊現象。這是因為兩相流中的氣泡可視作彈性體，當液體中產生壓力波時，小氣泡受到壓縮，又使周圍的液體加速，加速的液體又壓縮其他氣泡，使壓力波在兩相中的傳播速度明顯低于純液相，且小氣泡的收縮和膨脹消耗了部分能量，使得兩相流中的液擊壓力峰值低于純液相[24]。

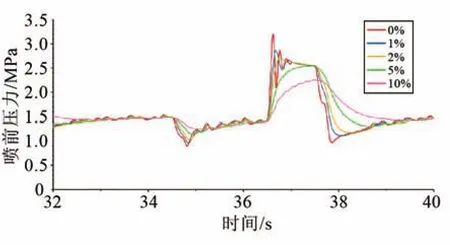
圖13 不同含氣率下液擊前后液體噴前壓力對比Fig.13 Comparison of the pressures before the nozzles with various void fraction

同樣可以由流體密度、體積彈性模量和黏度隨含氣率的變化趨勢分析知道，三者均隨含氣率的升高而降低，其中體積彈性模量的變化最為劇烈，而液擊壓力峰值隨流體密度和體積彈性模量減小而減小，隨黏性的減小而增大，表明在小含氣率下，含氣率主要是通過影響體積彈性模量來影響液擊現象的，表現為液擊壓力峰值隨含氣率的增加而減小。

3 結論

本文針對液氮供給系統的液擊現象問題，結合實驗數據開展了相關仿真研究，結論如下：

（1）對低溫液體供給系統中的典型部件，液氮柱塞泵、緩沖罐、調節閥等精確建模，在此基礎上搭建了供給系統的整體模型，進行了穩態工況下的仿真驗證計算，研究發現，主管路壓力、噴前壓力、噴射流量等主要參數與實驗值的平均誤差不超過2%；

（2）以液氮供給系統為研究對象，開展了液擊現象的仿真研究，模擬值與實驗值吻合良好，準確地描繪了因噴嘴連續啟閉而造成的噴射流量與噴前壓力的“陡升陡降”現象，解釋了實驗測量數據中壓力信號的高頻幅值衰減現象；

（3）分析了密度、體積彈性模量、黏性、含氣率對液擊現象的影響，其中液擊壓力峰值隨密度、體積彈性模量的減小而減小，隨黏性和含氣率的增大而減小。