神經網絡校正EKF在定位追蹤中的應用

部德強

神經網絡校正EKF在定位追蹤中的應用

部德強

（中國海洋大學 工程學院，山東 青島 266100）

針對毫米波雷達雖能獲取極坐標下目標數據，但無法直接獲取目標物位移分量且受系統噪聲影響無法進行高精度定位跟蹤的問題，提出一種利用反向傳播（BP）神經網絡校正擴展卡爾曼算法的無人帆船目標物的精確定位方法。通過擴展卡爾曼算法融合毫米波雷達數據，估計動態目標直角坐標系下的位移分量；并用BP神經網絡算法校正擴展卡爾曼濾波器，以降低動態目標物運動的不確定性及噪聲影響。仿真結果表明，該方法能夠降低系統噪聲的影響，更準確地進行目標物的定位追蹤。

無人帆船目標物；神經網絡；擴展卡爾曼；定位追蹤

0 引言

隨著海洋勘探活動的不斷深入，以風力作為驅動的無人帆船，因其具有更低成本、更長航時、更大范圍、更高時空分辨率等優勢，被越來越多地應用于海上探測活動[1]。當前對無人帆船定位追蹤目標物的研究較少，而隨著海洋環境的不斷惡化，加強對海面漂浮物的追蹤研究顯得十分迫切，因此本文提出了一種利用無人帆船實現海面目標物精確定位追蹤的研究方法。

由于目標追蹤的復雜性，直接獲取目標物精準定位存在一定的困難。國外提供了很多定位追蹤的研究方法[2-4]。國內文獻[5]針對傳統的定位技術誤差比較大，無法預測動態追蹤目標的實時位置等問題，提出了一種結合運動方程與卡爾曼算法的動態目標追蹤預測算法，有效地提高了定位精度，并對目標位置進行了實時預測。文獻[6]提出基于帶外源輸入的非線性自回歸(nonlinear autoregressive with exogenous inputs, NARX)神經網絡技術建立了單海況下的預測數據模型，通過船舶仿真器得到了艦船升降仿真模型，將NARX模型與傳統卡爾曼模型、反向傳播模型的預測結果進行對比，驗證了NARX神經網絡對復雜海浪環境具有更好的適應性和高海況下的高預測精度。文獻[7]針對傳統卡爾曼算法的噪聲方差不能自適應調節的問題，提出了將模糊控制器加入到卡爾曼算法中，對不同環境下的方差進行修正，適時調整噪聲力度，以提高卡爾曼算法的自適應能力與定位系統的抗干擾性。同樣針對噪聲方差不能自適應調節的問題，文獻[8]提出了將反向傳播（back propagation, BP）神經網絡算法加入到卡爾曼算法中，建立了基于BP神經網絡算法和卡爾曼算法相結合的船舶運動跟蹤模型，得到了船舶的運動狀態，實驗結果證明該算法精度高，噪聲抑制能力強，可以實現復雜海情下的船舶運動跟蹤，但該結果基于系統模型是線性系統的情況下，而現實中目標物的測量值與估計值為非線性關系，傳統標準卡爾曼算法不適用于非線性系統。本文將研究更接近實際的非線性系統模型，并通過BP神經網絡算法對擴展卡爾曼濾波器（extended Kalman filter, EKF）進行校正，以期提高擴展卡爾曼濾波器的性能，從而提高定位追蹤能力。

無人帆船通過全球定位系統（global positioning system, GPS）坐標轉換構建平面直角坐標系[9]，使無人帆船與目標物在同一坐標系下。為了更好地實現定位追蹤，需要獲得動態目標在此直角坐標系下的位移分量，激光雷達可以獲取相關數據。但考慮到激光雷達受環境、天氣影響較大，無法全天候精準作業，因此本文提出應用擴展卡爾曼算法融合毫米波雷達的數據估計目標物運動參數分量，并用BP神經網絡算法校正擴展卡爾曼濾波器，以提高擴展卡爾曼濾波器性能，使得無人帆船對目標物的定位追蹤精度得到較大提升。

1 控制系統流程

毫米波雷達在環境感知、目標跟蹤、路徑規劃及自主避障中都發揮了極其重要的作用[10]。將毫米波雷達獲得的目標數據作為觀測值，輸入到擴展卡爾曼濾波器中與估計值融合，擴展卡爾曼濾波器依次完成預測狀態值、預測協方差、計算卡爾曼增益、計算估計值、更新協方差5個步驟后將預測誤差、新息、卡爾曼增益作為BP神經網絡的輸入量并進行訓練，以估計誤差作為神經網絡輸出，與擴展卡爾曼濾波器輸出估計值求和，重新計算最優估計。控制系統流程如圖1所示。

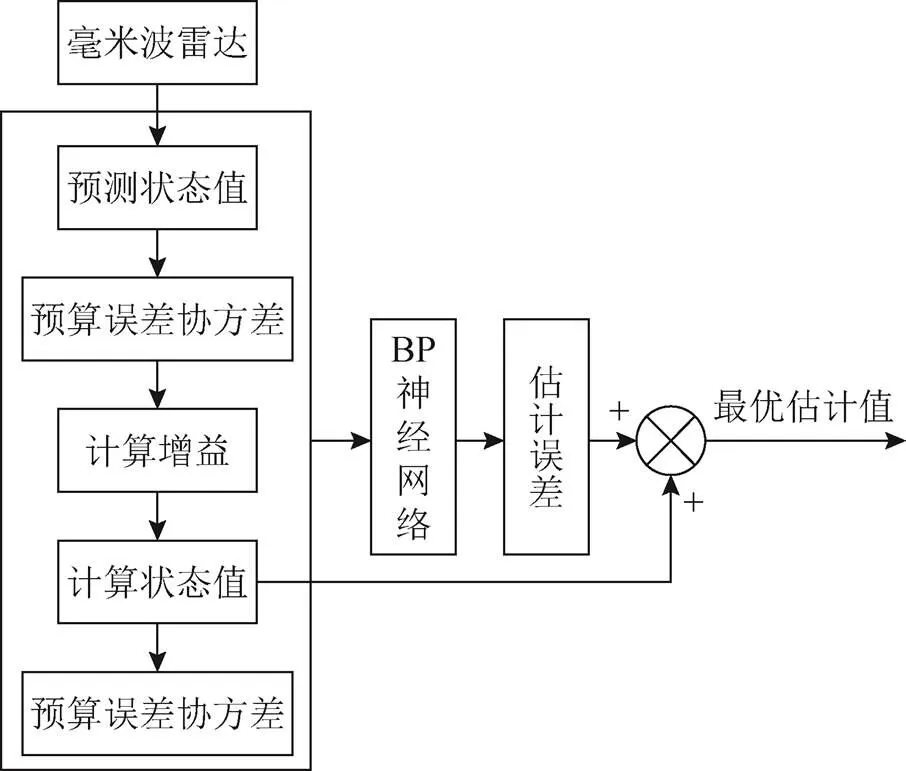
圖1 系統控制流程

2 目標物定位追蹤算法

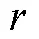
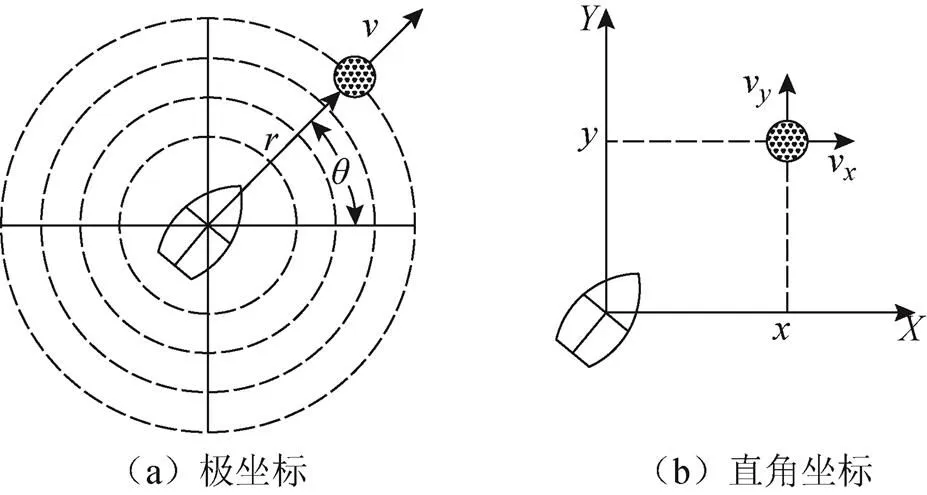
圖2 坐標轉換

2個坐標系之間的轉換關系為

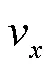
2.1 擴展卡爾曼算法

由式（1）可以看出，目標物的定位為非線性轉化過程，擴展卡爾曼算法可適用于非線性系統，首先建立基本系統模型為

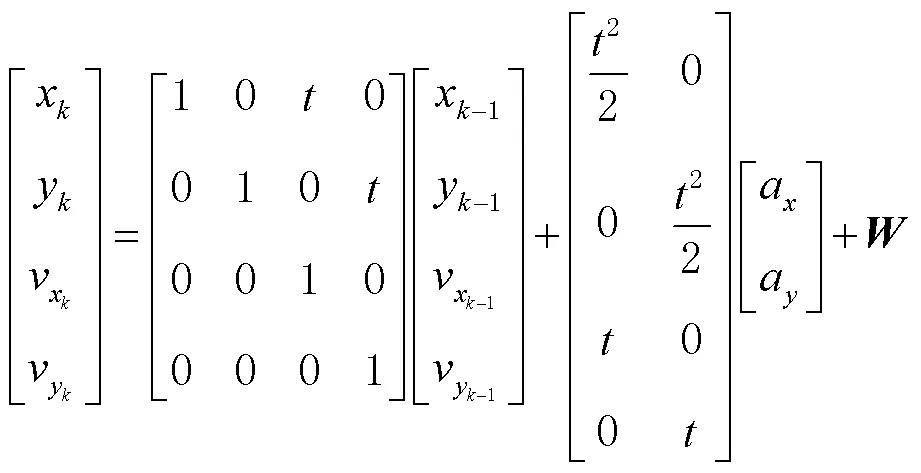
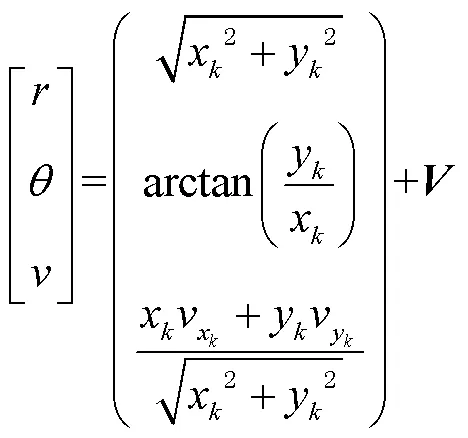
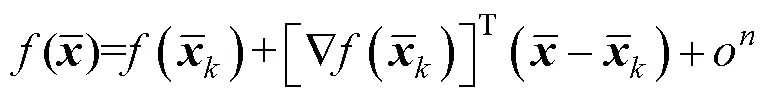
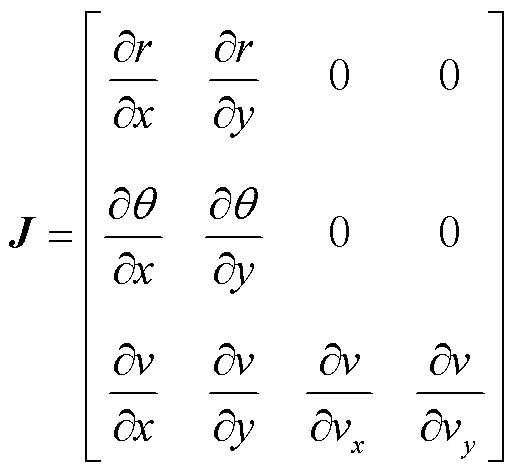
泰勒公式可將非線性系統線性化，線性化系統重新利用卡爾曼算法的5個公式估計位移分量與速度分量。卡爾曼算法5個公式為

采用日立 L-8800氨基酸自動分析儀對醬醪中氨基酸進行測定，測定過程委托貴州大學南區分析測試中心，樣品預處理采用GB/T 5009.124-2003進行處理。儀器進樣時泵1壓力為2～15 Mpa，流速為0.4 mL/min，儀器進樣時泵 2壓力為 0.5～2 MPa，流速為 0.35 mL/min。

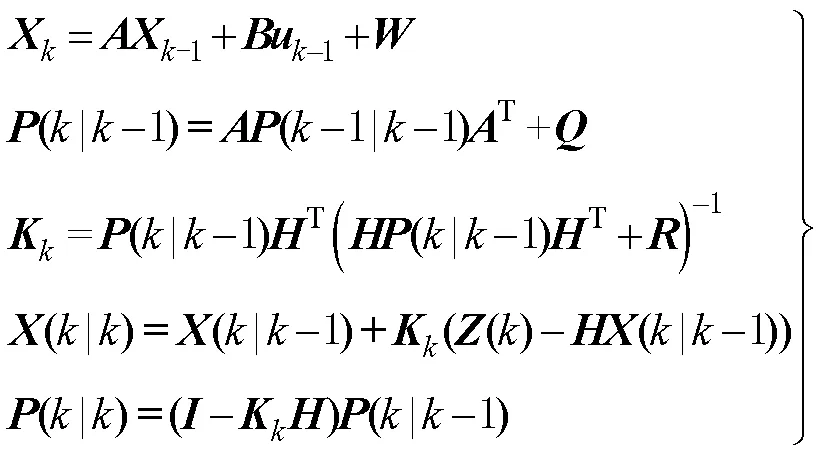
2.2 神經網絡算法校正擴展卡爾曼算法

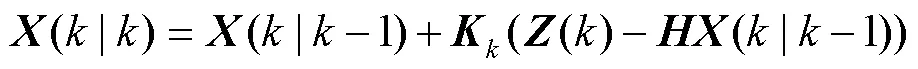
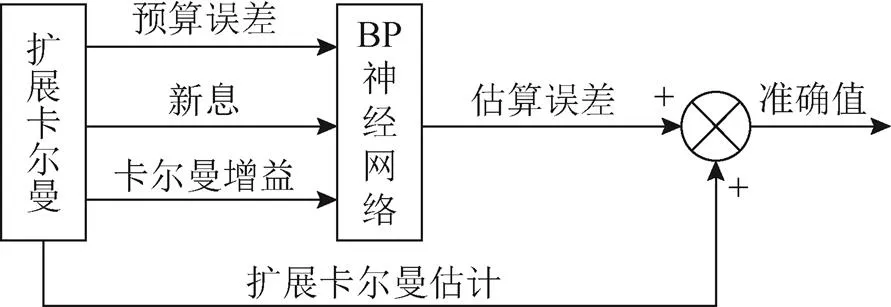
圖3 BP神經網絡優化EKF原理

確定神經網絡的輸入輸出參數后，須確定神經網絡的隱藏層層數和每層結點數。根據以往經驗，隱層的數量越多，對系統的非線性映射能力越強，但每層層數過高會導致神經網絡計算量過大，學習速度變慢和過擬合等情況[12]。擴展卡爾曼算法中預測誤差是4×1維矩陣，新息是3×1維矩陣，卡爾曼算法增益是4×3維矩陣，輸出估計誤差為4×1維矩陣，由式（7）[13]確定BP神經網絡輸入層神經元個數為19個。

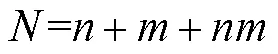
式中：為估計狀態維度；為新息維度。通常設置單層隱藏層且神經元節點個數足夠即可無限逼近真實值。為了提高系統的可靠性[14]，本文設置隱藏層的個數為2層。由式（8）[15]可計算出各層隱藏層的神經元個數為[8，8]。

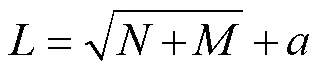
式中：為隱藏層神經元個數；為輸出層神經元個數；的取值為（1,10）。

BP神經網絡算法的訓練過程由信號的正向傳播和誤差的反向傳播2個部分組成。正向傳遞首先隨機初始化權重與偏置，權重的取值范圍為[-1, 1]，偏置的取值范圍為[0, 1]，然后由式（9）正向計算輸出值，進而計算誤差損失。

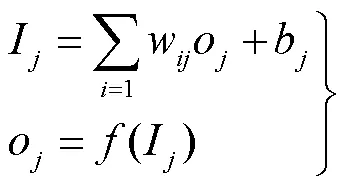
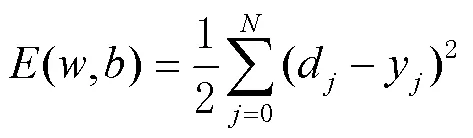
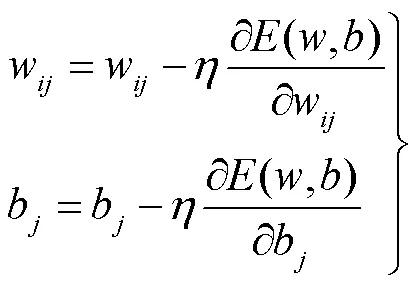
3 仿真與結果分析

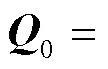
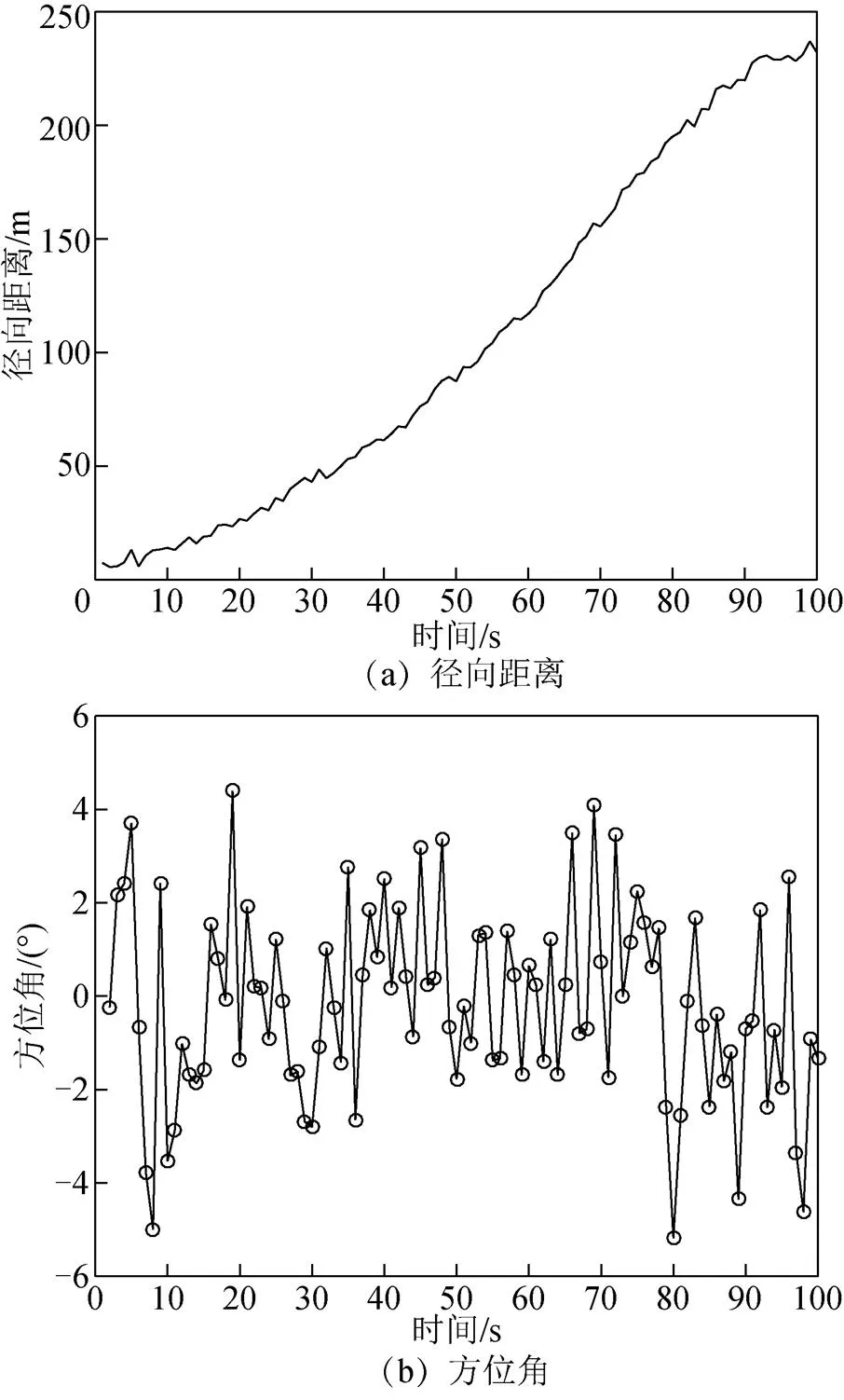
基于以上參數，在MATLAB中得到動態目標物與無人帆船的徑向位移圖、方位角變化圖和徑向速度變化，如圖4所示。

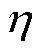
擴展卡爾曼算法與BP神經網絡擴展卡爾曼（BP-extended Kalman filter, BP-EKF）算法通過融合毫米波雷達數據可以獲得動態目標物的位移分量。2種算法的定位軌跡仿真如圖5所示。由圖5（a）可以看出擴展卡爾曼算法可以通過融合毫米波雷達數據完成動態目標的定位，但與圖5（b）BP神經網絡擴展卡爾曼算法的定位軌跡相比，在非線性較強的轉彎段出現相對較大誤差，誤差最大可到5 m左右，且在較為平緩的直線段也存在一定誤差。圖5（b）中，經過BP神經網絡算法校正的擴展卡爾曼算法定位軌跡精度大幅度提高，無論在非線性較強的轉彎部分還是直線部分，定位軌跡基本逼近期望數據，精度較高。

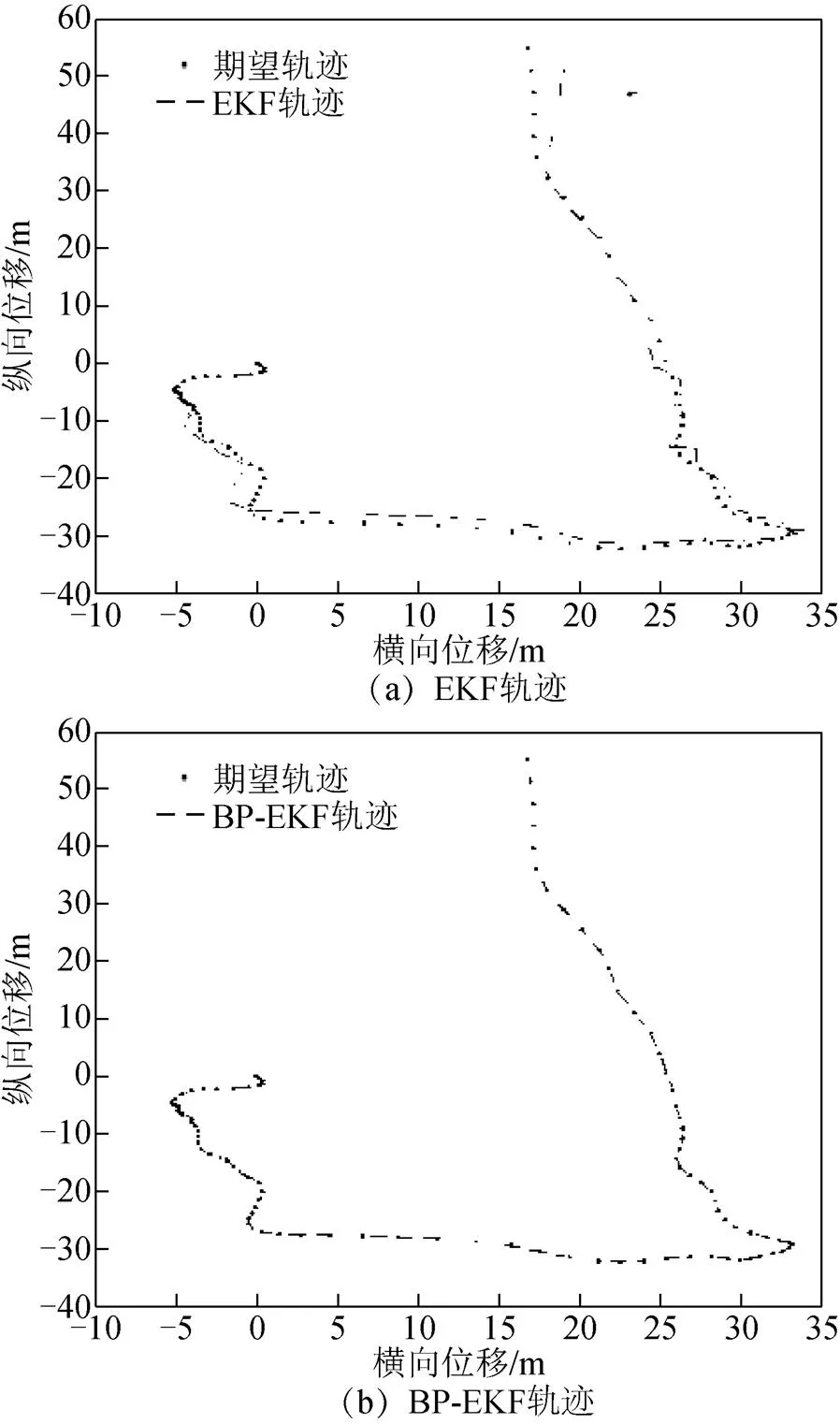
圖5 EKF、BP-EKF仿真對比

為了驗證BP神經網絡對擴展卡爾曼算法的校正作用，仿真另選取非線性較強的有交叉形態的動態目標物軌跡，如圖6所示。在圖6（a）中，擴展卡爾曼算法在交叉軌跡附近，濾波器不穩定出現不收斂趨勢且定位誤差變大；在圖6（b）中，BP神經網絡擴展卡爾曼算法定位更加穩定，且定位精度更高。

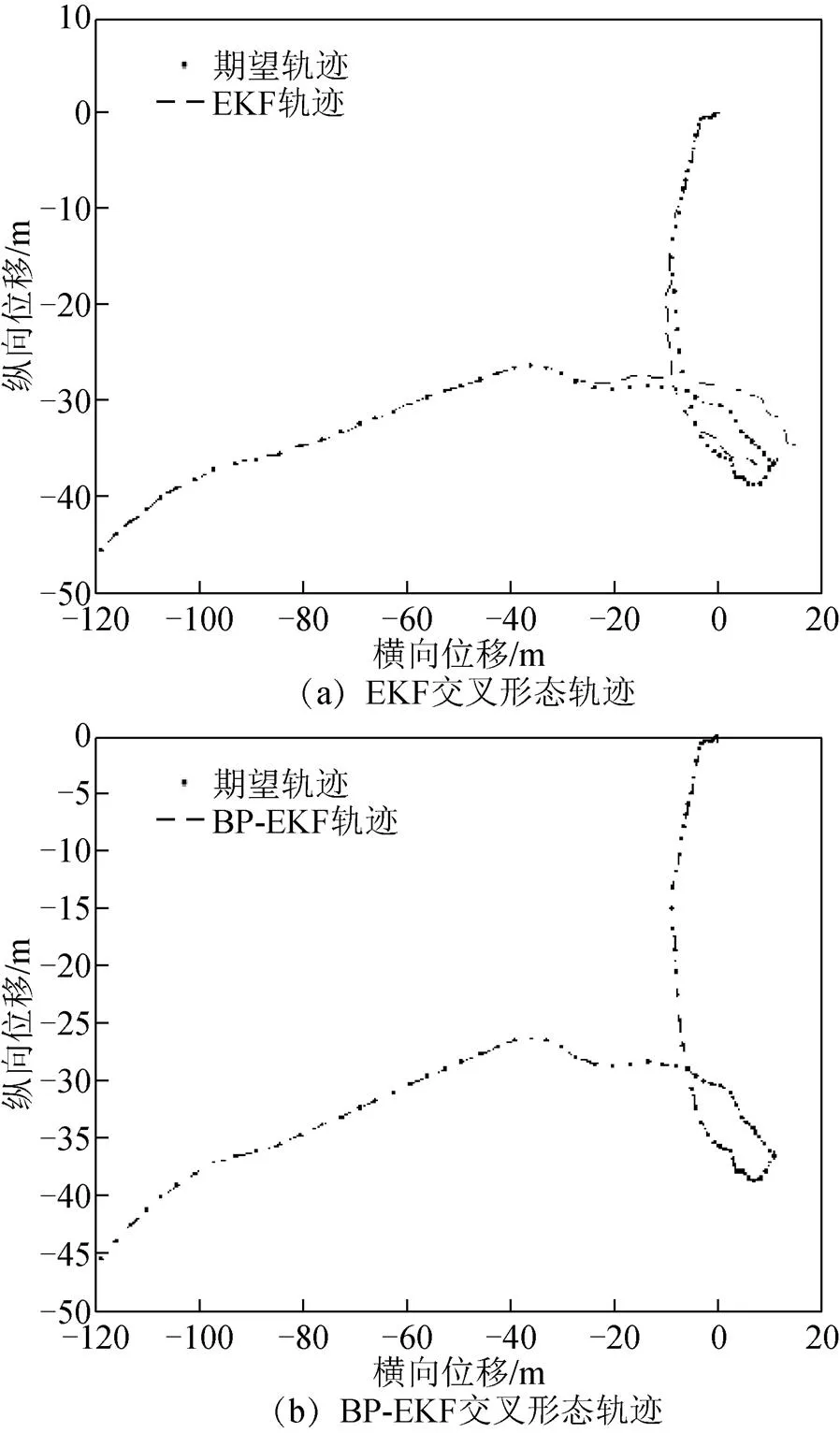
圖6 EKF、BP-EKF交叉形態軌跡仿真對比

為了驗證仿真數據的可靠性，經過多次仿真實驗統計分析，得到2種算法軌跡的橫向位移平均誤差與縱向位移平均誤差，如圖7所示。從圖7（a）、圖7（b）中可以看出：擴展卡爾曼算法軌跡的橫向位移平均誤差與縱向位移平均誤差在0.8 m范圍內，而BP神經網絡擴展卡爾曼算法橫向位移平均誤差與縱向位移平均誤差在0.2 m范圍內，精度提高較為明顯。

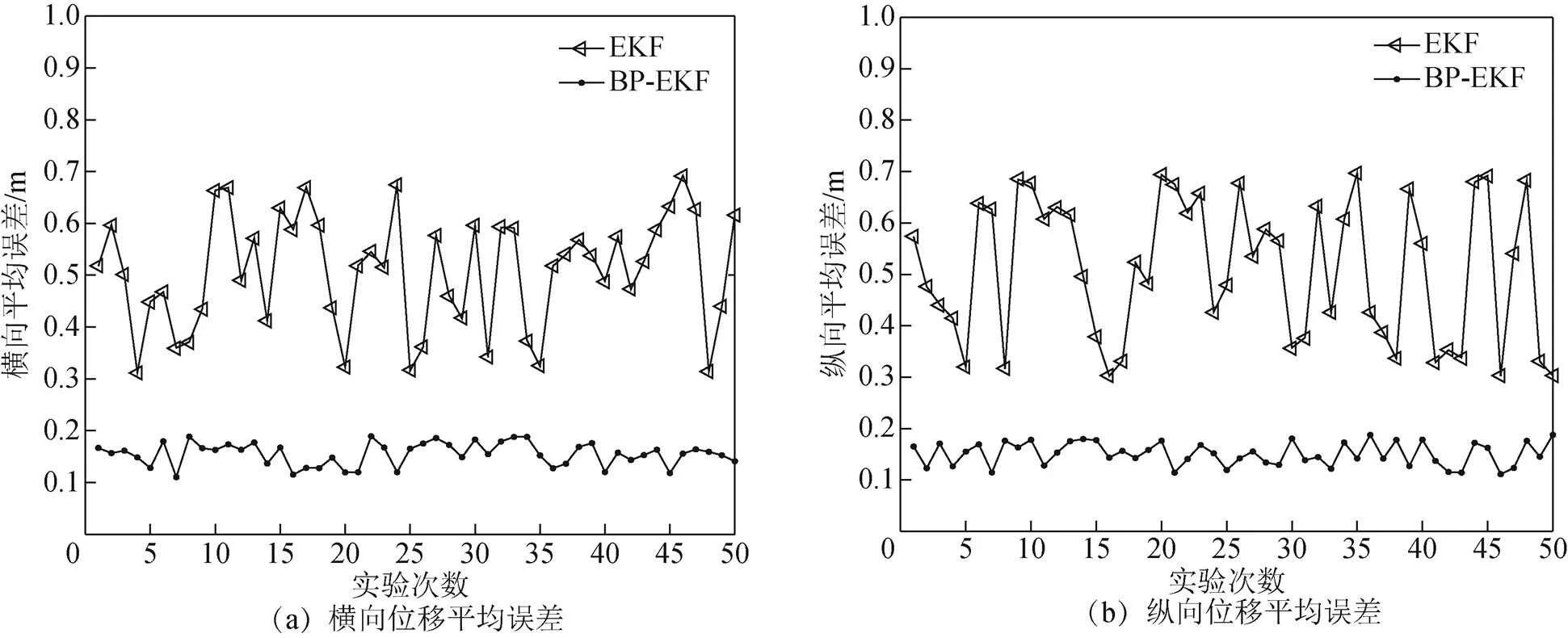
圖7 EKF、BP-EKF平均誤差對比

4 結束語

無人帆船追蹤目標的過程中，為了得到目標物的坐標位置，更好地實現目標物的定位追蹤，本文提出對毫米波雷達獲得的數據用擴展卡爾曼算法進行融合，同時用BP神經網絡算法對濾波器進行校正，來估計目標物的位移分量。

本文在MATLAB中建立目標物的系統模型，通過對比擴展卡爾曼算法與BP神經網絡優化擴展卡爾曼算法2種情況下得到的位移分量，經誤差分析得出：擴展卡爾曼算法能實現目標物的實時追蹤，但在復雜路況下有誤差變大的可能性；BP神經網絡校正擴展卡爾曼濾波器的算法，誤差小、可靠性高，性能優于單一擴展卡爾曼算法。加入神經網絡的擴展卡爾曼算法定位精度雖然得到提升，但如果神經網絡算法計算量大，將導致系統效率降低，因此本算法還可深入研究優化。

[1] 俞建成, 孫朝陽, 張艾群. 無人帆船研究現狀與展望[J]. 機械工程學報, 2018, 54(24): 98-110.

[2] CHIN L. Application of neural network in target tracking data fusion[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(1): 281-287．

[3] VAIDEHI V, CHITRA N, CHOKKALINGAM M, et al. Neural network aided Kalman filtering for multitarget tracking applications[J]. Computers & Electrical Engineering, 2001, 27(2): 217-228.

[4] JARADAT M A K, ABDEL-HAFEZ M F. Non-linear autoregressive delay-dependent INS/GPS navigation system using neural net-works[J]. IEEE Sensors Journal, 2017, 17( 4): 1105-1115．

[5] 王妍, 鄧慶緒, 劉賡浩, 等. 結合運動方程與卡爾曼濾波的動態目標追蹤預測算法[J]. 計算機科學, 2015, 42(12): 76-81.

[6] 樓夢瑤, 王旭陽, 陳瑞, 等. 基于NARX神經網絡的船舶升沉運動實時預測方法[J]. 中國艦船研究, 2020, 15(1): 48-55.

[7] 柏菁, 劉建業, 袁信. 模糊自適應卡爾曼濾波技術研究[J]. 信息與控制, 2002, 31(3): 193-197.

[8] 朱廣華. BP神經網絡和卡爾曼濾波相結合的船舶運動跟蹤[J]. 艦船科學技術, 2016, 38(20): 82-84.

[9] 肖體瓊, 陳怡群, 常春. GPS經緯度坐標轉平面坐標的簡化計算方法及精度分析[C]//中國農業工程學會. 中國農業工程學會學術年會論文集. 廣州: 中國農業工程學會, 2005: 49-52.

[10] 莊加興, 焦儂, 殷非. 毫米波雷達與激光雷達在無人船上的應用[J]. 船舶工程, 2019, 41(11): 79-82.

[11] HAYKIN S. Neural network principle[M]. Beijing: China Machine Press, 2004．

[12] 丁一, 張瑤, 李冠男. 神經網絡校正的EKF在水下被動目標跟蹤中的應用研究[J]. 小型微型計算機系統, 2020, 41(5): 897-901.

[13] 董志榮, 苗艷, 李艷麗. 目標定位和跟蹤的卡爾曼濾波加BP神經網絡的方法[J]. 火力與指揮控制, 1998，23(1): 3-5.

[14] 白宇駿, 徐曉蘇, 劉國燕. 神經網絡輔助卡爾曼濾波技術在組合導航系統中的應用研究[J]. 中國慣性技術學報, 2003,11(2): 42-45.

[15] 趙明, 何書前, 石春, 等. 一種基于神經網絡修正參數的卡爾曼濾波室內定位方法[J]. 現代電子技術, 2020, 43(7): 21-24.

[16] 李忠利, 劉小鋒, 陳修魁, 等. 基于信息融合的拖拉機組合導航定位系統研究[J]. 農業機械學報, 2020, 51(8): 382-390.

Application of neural network-aided EKF in localization and tracking

BU Deqiang

（College of Engineering, Ocean University of China, Qingdao, Shandong 266100,China）

Aiming at the problems that the millimeter-wave radar can obtain the target data under polar coordinates, but it can’t directly obtain the displacement component of the target object, and it is also unable to carry out high-precise location tracking due to the influence of systematic noise, the paper proposed a precise positioning method of unmanned sailboat target object using an extended Kalman algorithm aided by Back Propagation (BP) neural network: the extended Kalman algorithm was fused with the millimeter-wave radar data to estimate the displacement component of the dynamic target in Cartesian coordinate system, and the BP neural network algorithm was used to correct the extended Kalman filter for reducing the motion uncertainty of the dynamic target and the influence of noise. Simulational result showed that the proposed method could help reduce the influence of system noise, and achieve accurate target localization and tracking.

unmanned sailboat target object; neural network; extended Kalman; localization and tracking

P228

A

2095-4999(2021)06-0084-06

部德強. 神經網絡校正EKF在定位追蹤中的應用[J]. 導航定位學報, 2021, 9(6): 84-89.（BU Deqiang. Application of neural network-aided EKF in localization and tracking[J]. Journal of Navigation and Positioning, 2021, 9(6): 84-89.）

10.16547/j.cnki.10-1096.20210613.

2021-01-18

部德強（1991—），男，山東濟南人，碩士研究生，研究方向為海洋機電裝備與儀器。