基于KPCA-LSTM模型的石化生產過程故障診斷

劉會平，李大字

(1. 中國寰球工程有限責任公司 東南亞地區管理公司，新加坡 416202;2. 北京化工大學 信息科學與技術學院，北京 100029)

近年來，伴隨著信息技術的進步與發展，化工、電力、冶金等傳統工業都向著大型化、集中化的方向發展，現代工業體系中大型設備的智能化水平有了顯著提高，工作效率得到了大幅提升。然而，先進的智能化設備必然需要更為復雜的系統結構，所需控制的節點數目也就必然會增多，如果此時生產設備發生故障，按傳統的故障診斷方法是很難實現快速、準確的故障診斷。現代工業生產中會產生大量的運行數據，基于數據的故障診斷方法被廣泛使用[1-3]。

現代石油化工生產過程往往呈現一種非線性，系統結構較為復雜，產生的數據量非常大，而且系統內部產生的故障往往與多個可測變量存在復雜的關聯，大幅增加了利用數據做故障診斷的工作量。主元分析法(PCA)作為一種非常有效的降維技術[2]，對于處理線性數據降低維度的操作具有優良的特性，但無法處理非線性數據，此時對其加入核函數形成核主元分析法(KPCA)，可以實現非線性數據的降維[4-6]。處理復雜多模態，進行關聯、預測和記憶等能力[3]是當前神經網絡普遍擁有的特點。1997年專家提出的長短期記憶網絡(LSTM)對于時間序列數據具有很好的學習效果，同時解決了梯度消失的問題[7-9]。因此，本文提出了一種KPCA與LSTM相結合的故障診斷方法，通過田納西-伊斯曼(Tennessee Eastman, TE過程)化工仿真平臺檢驗過程故障診斷，結果表明： 該方法不僅可以有效減少運算量，還能提高故障診斷的準確率。

1 TE過程簡介

TE過程化工仿真平臺由美國著名化學公司Eastman開發，該平臺模擬實際流程工業的生產過程，工作過程中各節點與節點之間存在強耦合關聯，引入故障后，按連續時間采集工作數據，收集到的數據具有時變性和非線性。

在仿真平臺中，經過了22次的仿真運行，其中包括1次正常仿真運行和21次故障仿真運行。生產過程中有52個變量被觀測，每一次的仿真運行工作為48 h，采集數據時共采集960個時刻，在21次帶故障運行的過程中，每一次故障都是在第161個觀測時刻發生。

2 診斷流程

為解決流程工業中的故障診斷問題，考慮到實際生產過程中數據的非線性和時變性等相關因素，提出搭建KPCA-LSTM故障診斷模型。該種模型既可以去除不相關數據，減少運算量，提升運行速度，又能精準地診斷故障，實現故障數據的降低維度處理、故障檢測、故障預測與分類等功能[10-11]，最后選擇TE過程故障數據集來驗證該模型的性能。基于KPCA-LSTM故障診斷的流程框架如圖1所示。

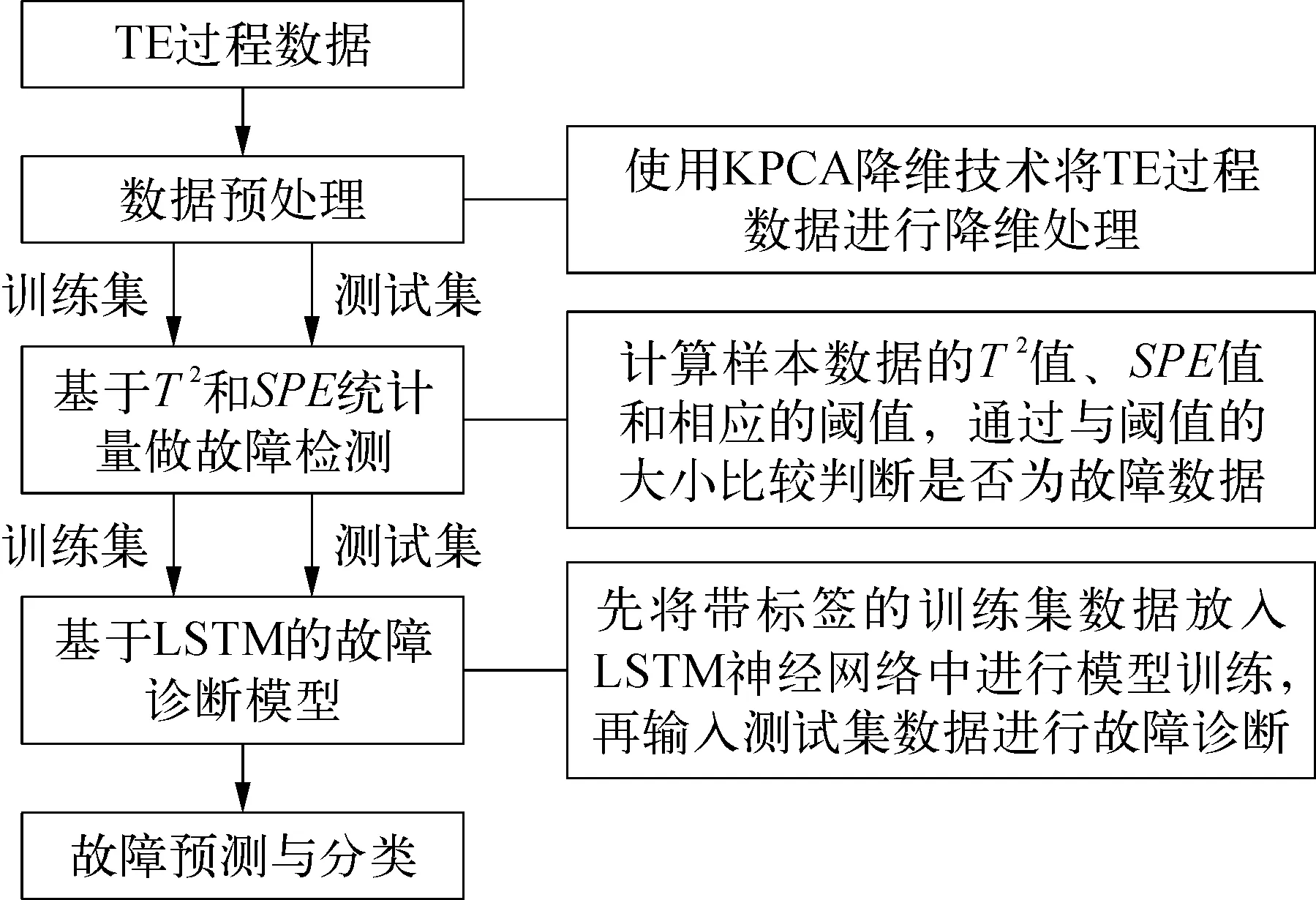
圖1 基于KPCA-LSTM故障診斷的流程框架示意

3 基于KPCA模型的故障檢測

3.1 KPCA原理

KPCA模型建立在PCA算法之上，為了提高對非線性數據的處理能力而提出來的。該方法挖掘非線性信息的能力很強，便于對非線性數據進行降維處理[4-5]。

假設有一個低維的、非線性的數據集可以寫成式(1)所示的矩陣形式，該矩陣有m×n個元素，表明數據集共有n個樣本，每個樣本數據有m個屬性。

(1)

由于該樣本數據是非線性的，因此用一個函數φ把該樣本數據映射到高維空間，在高維空間得到的數據矩陣φ(X)就是線性可分的了，結果如式(2)所示：

φ(X)=[φ(x1)…φ(xn)]

(2)

接下來計算協方差矩陣如式(3)所示：

φ(X)φ(X)Twi=λiwi

(3)

式中：λi——協方差矩陣的特征值。

根據向量的相關知識，空間中的向量wi可由這個空間中的所有φ(x)線性表達出來，如式(4)所示：

(4)

將式(4)中的wi代入到式(3)中，同時消除wi，得到結果如式(5)所示：

φ(X)φ(X)Tφ(X)α=λiφ(X)α

(5)

式中：α——φ(X)Tφ(X)的特征向量。

由于φ(X)是隱函數無法得知其具體表達式，因此引入核函數K來解決該問題，如式(6)所示：

K=φ(X)Tφ(X)

(6)

從而式(5)可以化簡得到式(7)：

Kα=λiα

(7)

因此可以求得核矩陣的特征值，計算出每一個特征值所對應的主元貢獻率，然后對主元貢獻率進行降序排列，求取累計主元貢獻率，當累計主元貢獻率超過90%時確定主成分，實現數據降維。

3.2 KPCA故障檢測

KPCA故障檢測與PCA方法類似，都是利用T2和SPE統計量進行檢測[6]，計算公式如式(8)～(9)所示：

(8)

(9)

式中：P——經KPCA降維后的矩陣，其控制限分別如式(10)和(11)所示：

(10)

式中：Tα——T2控制限；Qα——SPE控制限；1-α——置信度；Fα, k, n-k——服從第一自由度為k，第二自由度為n-k的F分布；cα——標準正態分布的置信極限，當數據的統計量超過其控制限時，認為該數據為故障數據。

4 基于LSTM的故障診斷模型設計

循環神經網絡(RNN)常被用于處理時間序列的問題，但當碰到有較長時間序列的問題時，該方法的效果通常不太理想。因此，對RNN改進得到LSTM，其內部結構使得它更適合對長時間序列進行分類[7]，具體結構如圖2所示。

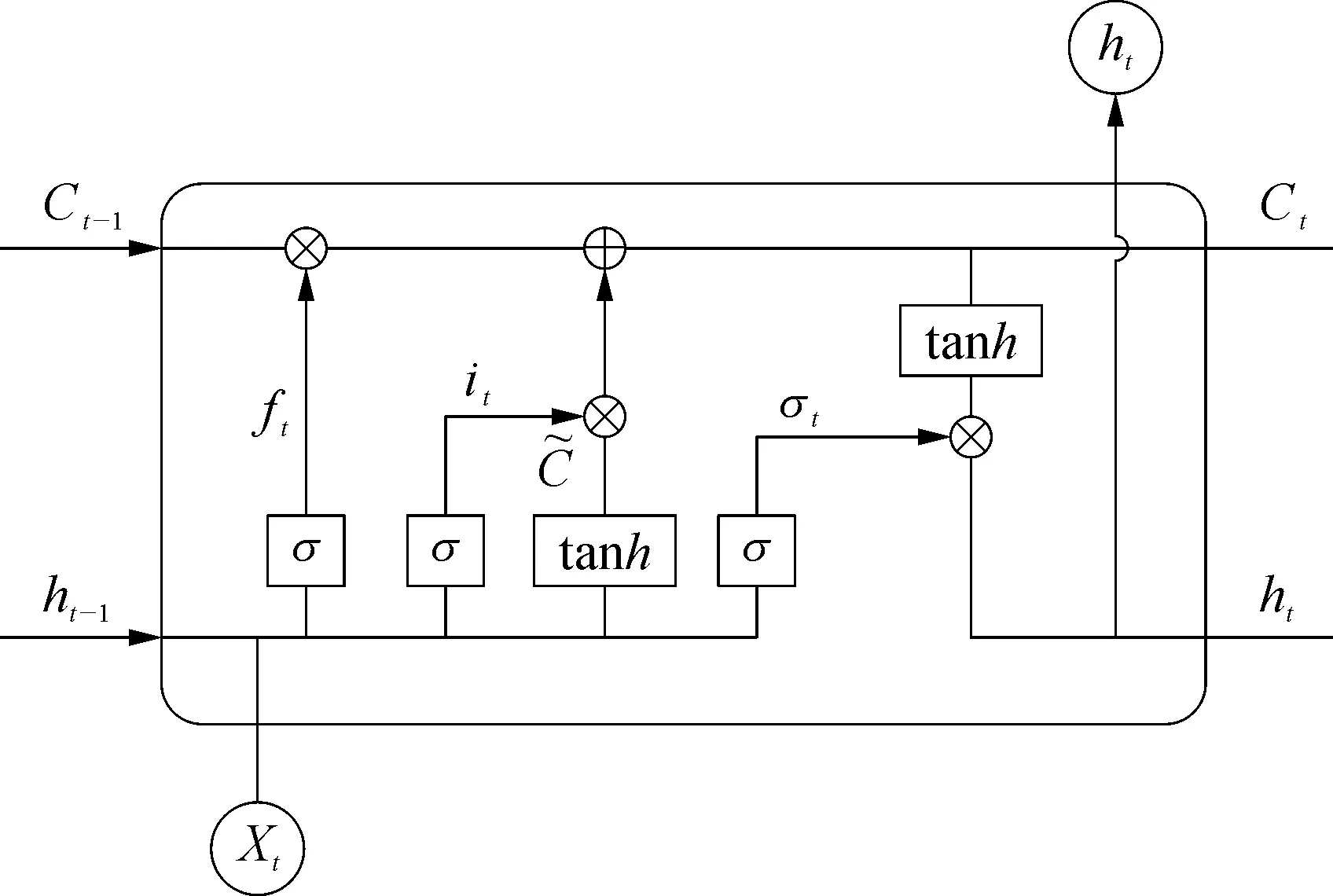
圖2 LSTM的內部結構示意

LSTM的結構主要分為以下三個部分[8-9]：

1)遺忘門。決定是否丟棄上一個細胞中的信息，計算公式如式(12)所示：

ft=σ(Wf×[ht-1,Xt]+bf)

(12)

2)輸入門。選擇留在細胞中的信息，更新細胞狀態，計算公式如式(13)所示：

(13)

3)輸出門。控制流向其他結構單元的信息流，計算公式如式(14)所示：

(14)

基于LSTM的故障診斷的模型如圖3所示。

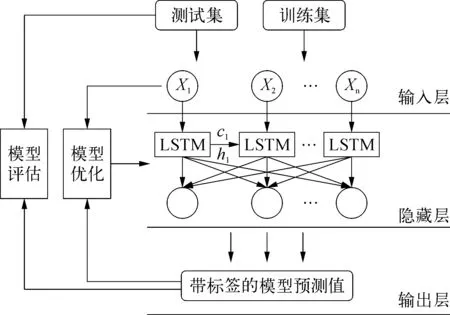
圖3 基于LSTM的故障診斷模型示意

5 實驗及結果分析

在TE過程仿真平臺工作過程中，從仿真的第160個觀測值開始引入故障。

5.1 KPCA故障檢測結果

將TE過程仿真平臺產生的21類故障數據和1類正常無故障運行數據作為訓練集和測試集，每1類數據的大小分別為960×52和480×52。KPCA中的核函數選擇最為常用的高斯核函數，σ取值設置為1×104。

圖4為第1類故障中52個觀測變量所對應的主元貢獻率，貢獻率的大小決定了該觀測變量對故障的影響程度，將貢獻率降序排列并進行累加，得到如圖5所示的累計主元貢獻率曲線，從圖5中可以看出，當主成分個數為12個時，累計主元貢獻率可達到90.47%。

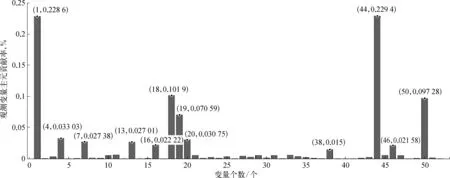
圖4 每個觀測變量的主元貢獻率示意

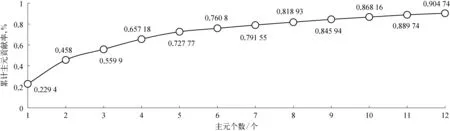
圖5 主成分個數與累計主元貢獻率曲線示意

分別計算降低維度后的數據的T2值和SPE值，按T2和SPE控制限的計算公式分別計算閾值，檢測結果分別如圖6和圖7所示。從圖6，7中可以看出，T2和SPE統計量分別在167和169時高于所計算的閾值，可判斷為故障，準確率分別為98.44%和98.23%，從而驗證了KPCA模型的準確性。

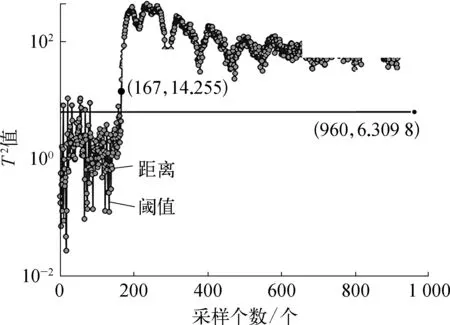
圖6 基于T2統計量的故障檢測曲線示意

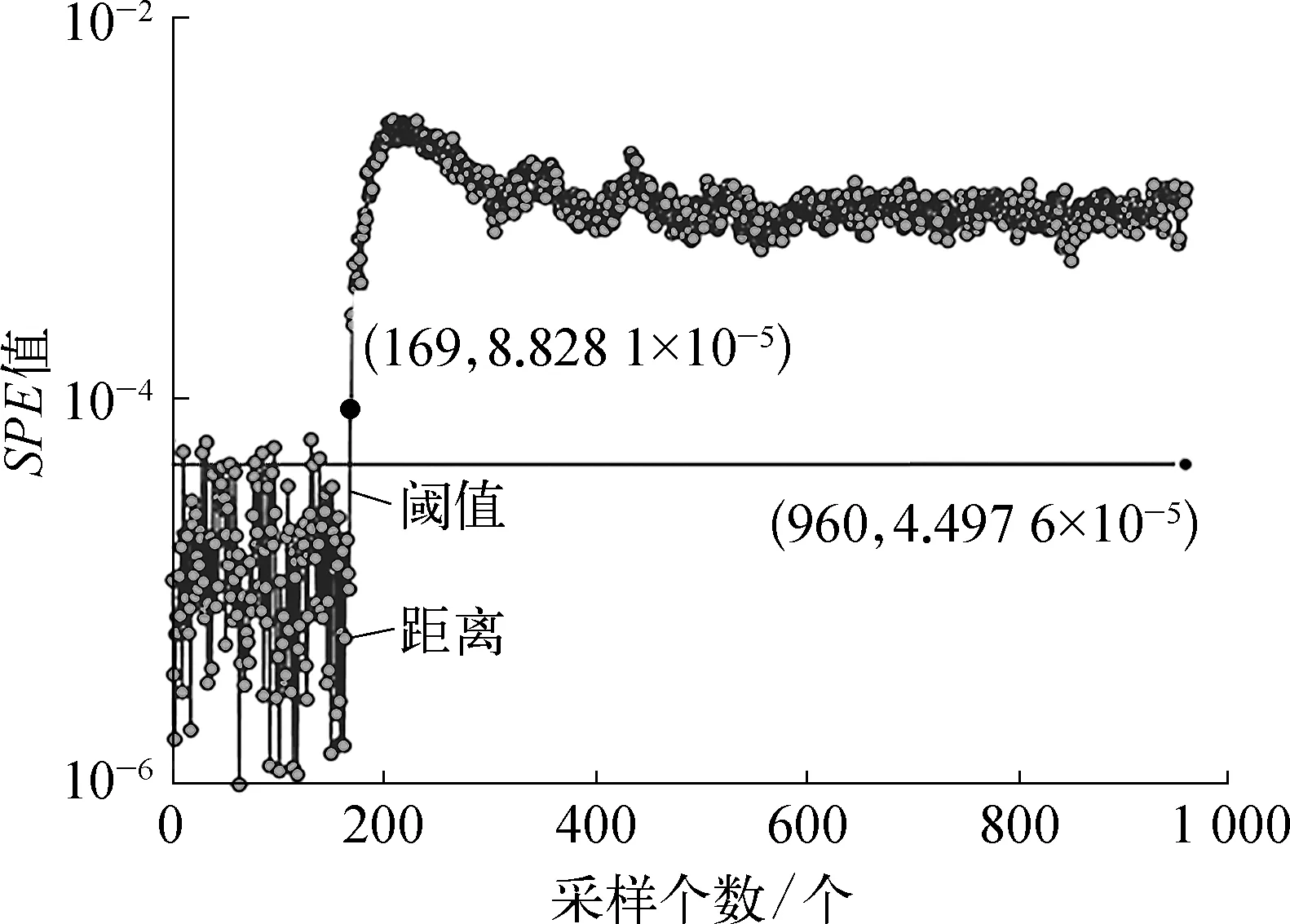
圖7 基于SPE統計量的故障檢測曲線示意

5.2 KPCA-LSTM故障診斷結果

經過KPCA模型降低維度后的樣本數據大小從52×960變成了12×960，將降維后的數據輸入LSTM模型進行診斷。降維數據與原始數據的訓練用時比較見表1所列。

表1 降維數據與原始數據的訓練用時比較

由表1可以看出，使用降低維度后的數據大幅提高了模型的訓練速度。表2為3類故障數據和5類故障數據進行故障診斷時的準確率比較。3類故障分別為1，6和18號故障，5類故障分別為1，2， 6，13和18號故障數據。

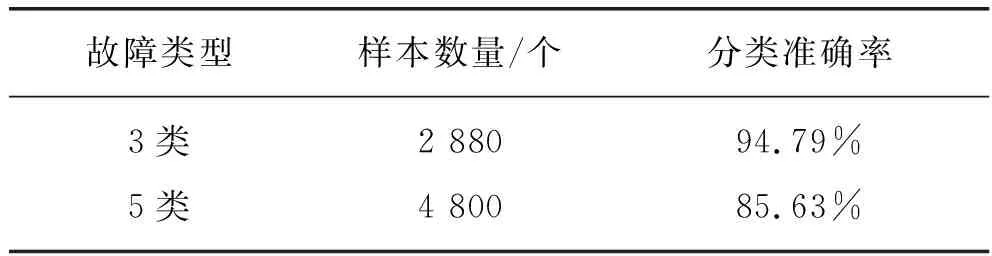
表2 3類和5類故障診斷準確率比較

由表2可知，LSTM可以較為準確地診斷出故障類型，但是隨著故障種類的增多，診斷準確性有所下降。

6 結束語

本文采用KPCA和LSTM相結合的方法對TE過程故障進行診斷，實驗結果表明該方法可以有效地檢測到故障的發生并且準確判斷出故障的類型，同時經過KPCA降維使得LSTM的訓練時間大幅縮減，提高了診斷的速度。