基于廣義最大Versoria準則的稀疏自適應濾波算法

歐躍發，楊鳴坤，慕德俊，柯捷，馬文濤

（1.北部灣大學機械與船舶海洋工程學院，廣西欽州 535011；2.桂林航天工業學院計算機科學與工程學院，廣西桂林 541004；3.西北工業大學網絡空間安全學院，西安 710072；4.西安理工大學電氣工程學院，西安 710048）

0 引言

在許多實際工程系統中，其系統模型脈沖響應參數往往具有稀疏特征，稱其為稀疏系統，如水聲信道以及超寬帶通信系統［1-2］等。如今，稀疏系統參數辨識已成為目前參數辨識研究中的熱點問題。現在，研究者們提出了各種稀疏自適應濾波算法來辨識稀疏參數，其主要思想是將系統稀疏特性作為先驗知識考慮到算法設計中，從而實現優良的稀疏參數估計性能。受最小絕對收縮選擇算子［3］及壓縮感知［4］的啟發，文獻［5-6］將l1-范數及加權l1-范數作為稀疏懲罰約束引入最小均方（Lest Mean Square，LMS）算法構建稀疏自適應濾波器，其中主要包括零吸引LMS（Zero-Attracting LMS，ZALMS）、加權零吸引LMS（Reweighted ZALMS，RZALMS）。事實上，l0-范數是最佳的稀疏約束條件，但由于其優化計算是NP難問題，所以文獻［7］中使用拉普拉斯函數作為l0-范數的逼近形式，提出了l0-LMS。在近期研究中，許多不同形式的稀疏LMS算法被提出，包括lp-范數約束的LMS 及歸一化LMS（Normalized LMS，NLMS）算法、稀疏最小均方/四階算法［8］和低復雜度稀疏仿射算法等［9-10］。

上述稀疏自適應濾波算法在稀疏參數辨識方面具有良好的性能，但多以最小均方誤差（Mean Square Error，MSE）作為代價函數，即其僅在高斯噪聲假設下具有最優性能。然而，在許多實際應用場景中，噪聲往往具有非高斯特性［11-13］，比如無線信道的多址干擾、回聲干擾消除的重音、生物噪聲或各種水聲信道冰裂聲等。在此類環境中，特別當觀測噪聲具有脈沖特征時，基于MSE 準則的方法則具有一定性能缺陷。為解決非高斯噪聲干擾環境下的稀疏參數辨識問題，目前也有相關研究者提出了魯棒性自適應濾波算法［12-13］，如最小絕對偏差（Least Absolute Deviation，LAD）［14］算法、最大互相關熵準則（Maximum Correntropy Criterion，MCC）算法［15-16］、反雙曲正弦函數算法［17］、最大Versoria 準則（Maximum Versoria Criterion，MVC）算法［18-19］等。其中Versoria 函數最早是用來代替粒子群算法中的Sigmoid函數，以提供自適應慣性權重因子來避免指數運算，并確保低穩態失調，使其主要扮演著變步長的角色。文獻［19］則將Versoria 函數作為代價函數并定義了廣義Versoria 函數，在此基礎上推導出了廣義最大Versoria 準則（Generalized MVC，GMVC）算法，該算法可有效地解決非高斯噪聲干擾下的系統辨識問題。本文則主要借鑒GMVC 的優勢，結合稀疏懲罰函數提出稀疏GMVC算法，以實現脈沖噪聲干擾下的稀疏系統參數辨識。

稀疏懲罰約束是稀疏自適應濾波算法構成的主要組成部分。稀疏約束實質上就是要使得待辨識參數向量中非零參數最少，由此便可使用l0-范數作為約束條件。但l0-范數最優化是NP-hard 問題，因此在實際應用中往往使用l0-范數的逼近函數，如l1-范數及加權l1-范數。而互相關熵誘導維度（Correntropy Induced Metric，CIM）［20］可通過選擇合適核寬度來無限逼近l0-范數。基于此，本文將重點以CIM 為稀疏懲罰約束來構建稀疏GMVC——帶有CIM 約束的GMVC（GMVC with CIM constraints，CIMGMVC）算法，并對其均方收斂性能進行分析研究。

1 廣義Versoria準則

考慮如式（1）所示的有限脈沖響應（Finite Impulse Response，FIR）模型來研究基于廣義Versoria 準則的穩健稀疏參數估計算法。設FIR 系統模型中輸入信號向量為u(n)=[u(n)，u(n-1)，…，u(n-L+1)]T，系統參數向量記為wopt=[wopt，1，wopt，2，…，wopt，L]T，L為向量長度。在此僅考慮系統參數為實值情形，且具有稀疏特征，即大部分參數值為0。則接受端信號d(n)可表示為：

其中：v(n)表示n時刻接收端的干擾噪聲。由于系統參數向量wopt往往未知，需要使用自適應算法對其進行辨識，在此設w(n)=[w1(n)，w2(n)，…，wL(n)]T為系統參數向量在n時刻的估計，則系統的估計輸出y(n)=wT(n)u(n)。此時可定義系統瞬時誤差e(n)=d(n)-y(n)。在相關稀疏參數辨識研究中，往往假設噪聲服從高斯分布。然而在許多實際環境中，人為因素以及一些自然噪聲都具有脈沖特性，這意味著實際環境中的噪聲往往具有非高斯特性。而本文則主要是基于Versoria 函數研究一種新型稀疏自適應濾波算法以解決稀疏系統辨識過程中非高斯噪聲干擾問題。

定義合適且高效的代價函數是設計自適應濾波算法的關鍵。受廣義高斯概率密度函數啟發，文獻［20］定義了廣義Versoria函數為：

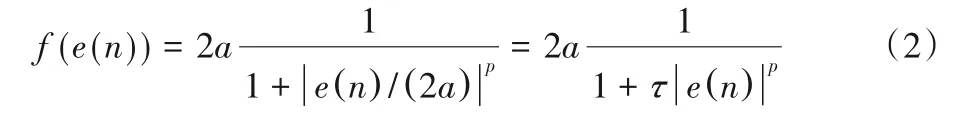
其中，p>0 表示形狀參數，τ=(2a)-p，當p=2 時，其退化為原始Versoria 函數。根據式（2），定義基于Versoria 函數的代價函數為：

其中，E[]表示期望算子。由式（3）可知，當脈沖干擾出現在誤差中時，則會有J(w(n)) →0，其具有抑制脈沖噪聲干擾的作用。當誤差非常小時，易知J(n) ≈。此時，廣義Versoria代價函數將類似于傳統的p-power代價函數。由式（3）可進一步定義瞬時代價函數（即移除期望算子）為：

其梯度可計算為：

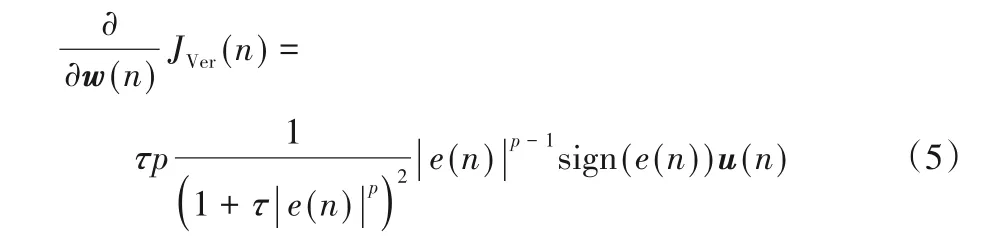
此時應用隨機梯度上升方法得到廣義最大Versoria 準則（GMVC）算法的權值更新方程為：

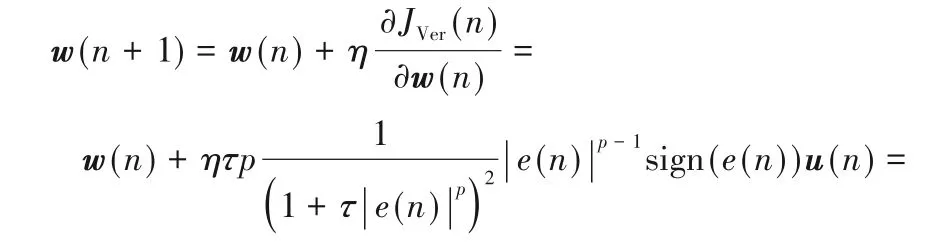
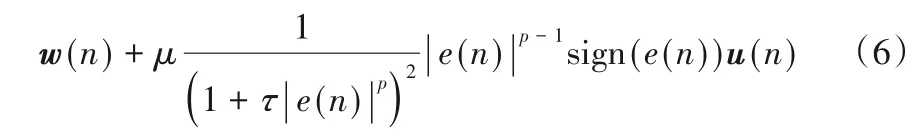
其中：μ=ητp表示步長；sign(?)為符號函數。sign(?)定義如下：

在GMVC算法中，當p=1、τ=0時，其退化為傳統的最小絕對偏差（Least Absolute Deviation，LAD）算法。在式（6）中若設μ(n)=μ，則易知GMVC 算法會等價于步長為μ(n)的變步長LMS 算法。對于變步長LMS 算法，希望在自適應迭代的初始階段收斂要快，所以需要較大的步長，而在自適應的后期需要較小的步長來保證小的穩態誤差。基于此可以看出：1）當GMVC 算法沒有收斂時，誤差項|e(n)|非常大，這就使得μ(n)也具有較大的值，因此GMVC 算法具有快的收斂速度；2）當GMVC 算法達到收斂狀態時，誤差|e(n) |也非常小，這便使得步長和精度都非常小。以上兩點說明了GMVC算法的優勢。

2 基于CIM約束的稀疏Versoria算法

2.1 Correntropy誘導的度量

CIM 作為互相關熵誘導度量，其在選擇合適的核寬度時具有l0-范數的行為［15］。本文將以CIM作為稀疏懲罰約束。若設向量x=[x1，x2，…，xN]T，則選擇高斯核的CIM 作為l0-范數的形式如下：

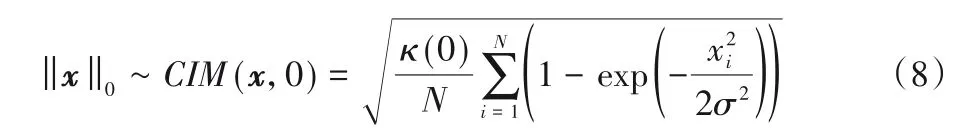
為了計算簡便，常使用式（8）的平方形式作為l0-范數的逼近，即：

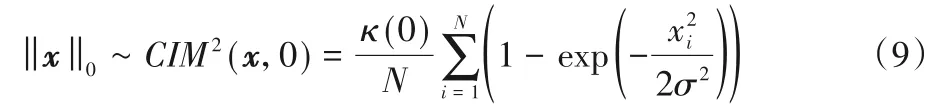
在式（8）中，對于?xi≠0，且 |xi|>δ，若使得σ→0，此時CIM 就可以無限逼近l0-范數，其中δ是一個小的正數。CIM 作為l0-范數的逼近是稀疏懲罰約束的一種很好的選擇，可使用梯度映射方法得到CIM的梯度向量如下：

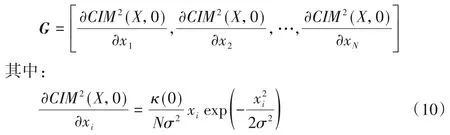
2.2 稀疏最大Versoria算法

為了結合稀疏懲罰約束CIM來研究稀疏Versoria算法，現定義如下代價函數：

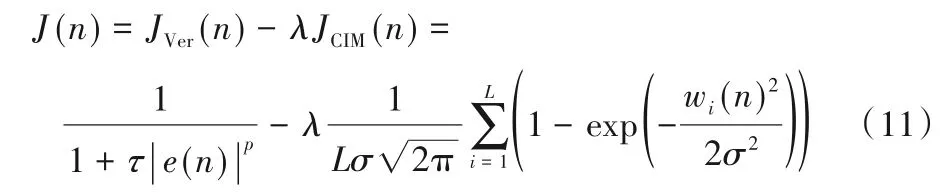
其中，ρ=ηλ為零吸引控制因子。式（12）向量形式為帶有CIM約束的GMVC（CIMGMVC）算法的迭代方程，如式（13）：

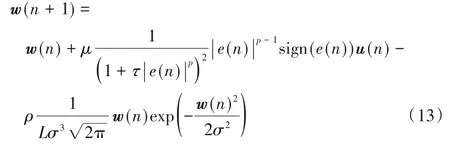
對于CIMGMVC 算法，當選擇合適的p值可使其對于脈沖噪聲具有魯棒性；同時又由于引入了稀疏懲罰約束，使得它適用于受脈沖噪聲干擾環境下的稀疏系統辨識和信道參數辨識問題。

3 收斂性分析

本章將進一步分析所提CIMGMVC 算法的平均和均方收斂性。為分析簡單，將式（13）表示為：

假設1 輸入信號{u(n)}獨立同分布于零均值高斯分布。

假設2 噪聲信號{v(n)}均值為0、方差為，且獨立于輸入信號{u(n)}。

假設3 誤差非線性項f(e(n))與輸入信號{u(n)}及參數向量w(n)相互獨立。

假設4 參數向量w(n)及g(n)與輸入信號{u(n)}相互獨立。

假設5 期望E[f(e(∞))]為有限值。

假設1、2 在參考文獻［21-22］中也得到了應用，其意味著當參數向量存在于最優參數向量wopt的某近鄰域時有效。

3.1 平均收斂性

定義參數誤差向量為：

記(n)的均值與自相關矩陣分別為：

其中Δ(n)的定義如下：

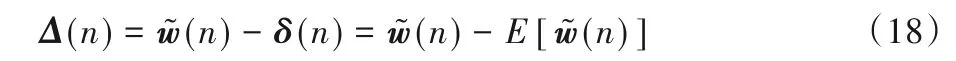
結合式（1）、式（14）及式（15）得到：

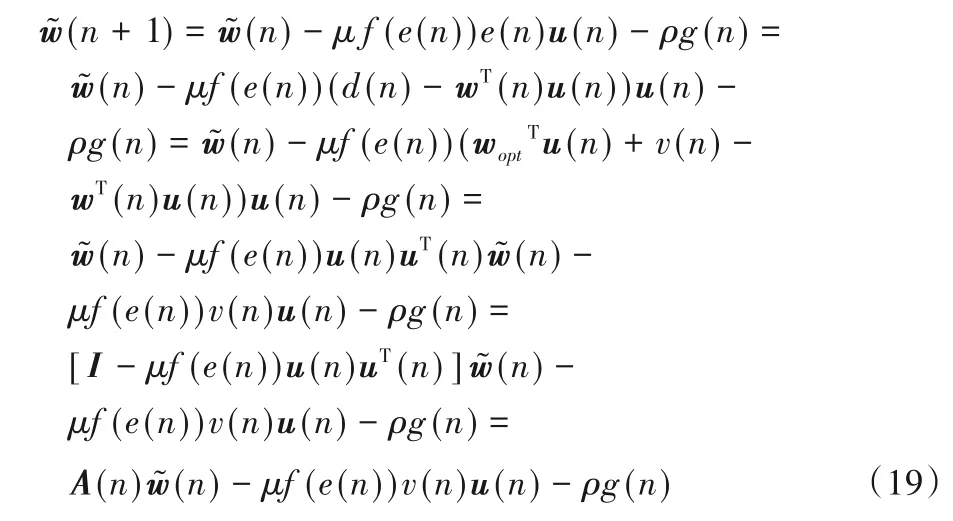
其中A(n)=[I-μf(e(n))u(n)uT(n)]。對式（19）兩邊取期望，且使用獨立假設1、2與3，可得到：

通常情況下，待估計的參數wi(n)是有限的，結合式（25），可知即使wi(n)趨向于無窮，則g(wi(n))仍然有限。根據該結論，可知對于CIMGMVC算法，E[g(∞)]仍然是有限的。

在以上分析的基礎上，結合假設5，可知對于CIMGMC 算法，E[w(∞)]都會趨近于有限向量。因此可知E[w(n)]將收斂于E[w(∞)]，如式（22）所示。至此算法的平均收斂性得以說明。

3.2 均方收斂性

在式（19）兩邊分別減去式（20），且應用式（18）可得到：

在式（32）中，E[w(n)]與C(n)有界，可知E[w(n)CT(n)]收斂。綜上可知當且僅當所提自適應算法滿足如式（33）所述條件時，算法則會達到穩態。

因此由上述不等式（33）可得到：

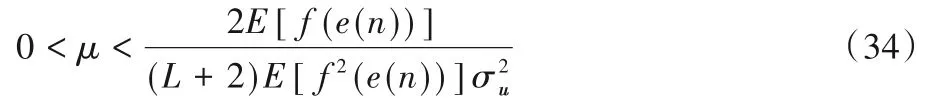
此結果表示，當步長滿足式（34），就可以保證算法的收斂性。據上述均方收斂性分析易知稀疏CIMGMVC 算法的均方收斂性更多依賴于自適應濾波器項，而非稀疏懲罰項。

4 仿真與結果分析

將所提算法應用于脈沖噪聲干擾環境下的稀疏系統參數辨識場景，以此來驗證所提算法的性能。將本文所提CIMGMVC 算法主要與LMS、ZALMS、RZALMS、LAD 和零吸引LAD（Zero-Attracting LAD，ZALAD）算法進行性能比較。在仿真實驗中，輸入信號為服從零均值單位方差的高斯隨機序列，實驗結果由200 次蒙特卡洛仿真實驗結果平均計算得到。均方偏差（Mean Square Deviation，MSD）作為算法性能評價準則，其定義如下：

設系統參數向量長度M為20。定義系統稀疏度Ds為：

其中，Nnon?zero為系統參數向量中非零元素的個數。本文選擇α-stable分布模型來模擬脈沖噪聲，其概率密度函數如下：

其中：

在上述分布中，α∈(0，2]表示特征指數，刻畫該分布脈沖嚴重度，α越小，脈沖強度越大；-∞<δ<+∞為位置參數，刻畫α-stable 分布的均值或中值；β∈[-1，1]是對稱參數，當β=0 時，服從α-stable 分布的隨機變量的概率密度函數關于位置參數δ對稱；γ>0 表示分散系數，刻畫α-stable 分布隨機變量可能取值的離散程度。當β=0、δ=0時，稱其為對稱α-stable分布，即SαS。定義噪聲模型參數向量為Vα?stable=(α，β，γ，δ)。

4.1 時變稀疏系統參數辨識

本節驗證算法在時變稀疏系統參數辨識中的收斂性。設置噪聲模型參數向量Vα?stable=(1.2，0，0.2，0)，算法中各參數分別設置為μ=0.01、ρ=0.0005、τ=0.001 和σ=0.05、p=1.2。稀疏系統模型的稀疏度為3/20。圖1 為各算法在時變稀疏系統參數辨識中的收斂曲線結果。

從圖1中可知，在脈沖噪聲環境下，以MSE 為代價函數的LMS 算法和ZALMS 均無法收斂，具有較大的波動，表明該類算法在脈沖噪聲環境中不穩定，同時也說明構建魯棒稀疏自適應算法的必要性。相應地，可看到LAD、ZALAD、RZALAD、GMVC和所提出的CIMGMVC則具有較好的魯棒性能。然而，對于這類稀疏系統參數辨識問題，可知CIMGMVC 算法的穩態精度明顯高于其他算法。該結果再次表明了當選擇合適的核寬度后，CIM 的確可以很好地逼近l0-范數。這也驗證了本文所提算法的優越性。

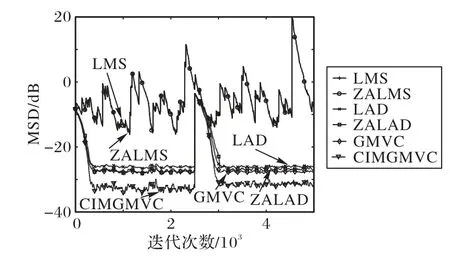
圖1 不同算法的收斂曲線比較Fig.1 Comparison of convergence curves of different algorithms

4.2 自由參數p對CIMGMVC算法性能的影響

在不同α-stable 噪聲環境下研究所提CIMGMVC 算法中自由參數p對其性能的影響。在本實驗中選擇噪聲分布參數向量Vα?stable=(1.6，0，0.2，0)，研究p值對GMVC 和CIMGMVC算法的影響。進行100 次蒙特卡羅實驗，每次實驗進行5000次迭代運算，本仿真通過選擇最后200 次結果來計算穩態MSD。選擇不同p值時的MSD 結果如圖2 所示。由圖2 可以看出，在不同脈沖噪聲干擾下，CIMGMVC 算法的穩態精度均優于GMVC算法，該結果再次表明CIMGMVC算法在引入CIM作為稀疏懲罰約束后可以有效提升此類稀疏系統參數辨識的精度。

圖2 不同p值下GMVC算法及CIMGMVC算法的穩態性能比較Fig.2 Comparison of steady-state performance of GMVC algorithm and CIMGMVC algorithm with different values of p

4.3 CIMGMVC算法的魯棒性能

本節研究CIMGMVC 算法在不同α（0.5、1、1.2、1.4、1.6、1.8）值時算法的魯棒性，同時與GMVC 算法進行比較研究。該算法在不同脈沖噪聲下的穩態MSD 結果如圖3 所示。從圖3結果也易觀察到，當在較大脈沖噪聲（小的α）干擾下算法具有較大的MSD，而隨著α值的增大，則穩態誤差較低。但同時也發現，該算法在不同脈沖干擾下，其結果均能收斂，驗證了該算法的魯棒性。另外，也很容易得出對于不同脈沖強度的干擾，可以通過選擇合適的自由參數來增強其估計性能。

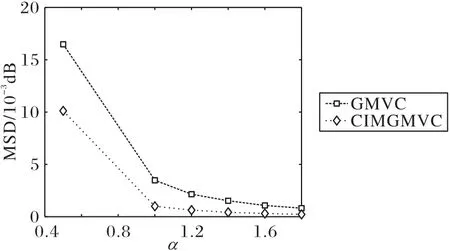
圖3 不同α值下GMVC算法及CIMGMVC算法的穩態性能比較Fig.3 Comparison of steady-state performance of GMVC algorithm and CIMGMVC algorithm with different values of α

4.4 核寬度σ對CIMGMVC算法性能的影響

核寬度σ是影響CIMGMVC 算法性能的一個主要自由參數，這里繼續研究其對CIMLMP 算法性能的影響。本仿真實驗中選擇核寬度分別為：0.001、0.005、0.01、0.05、0.1 及0.5，噪聲參數向量與上述仿真一致。圖4 給出了算法的收斂曲線。由圖4 可以看出，對于不同的核寬度，CIMGMVC 算法具有不同的收斂性；還可以看出當核寬度在0.05 附近時，算法具有最優性能。而如何選擇最優核寬度來更加逼近l0-范數可作為未來的一項研究工作。

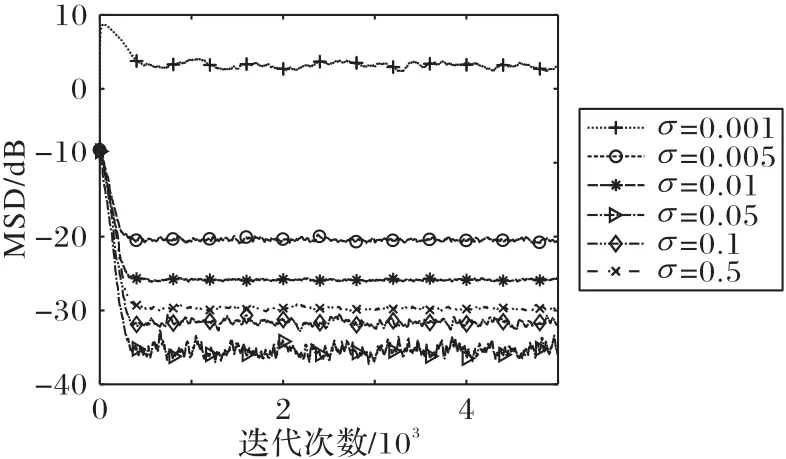
圖4 不同核寬度σ下的CIMGMVC算法的收斂曲線Fig.4 Convergence curves of CIMGMVC algorithm with different values of kernel width σ

4.5 步長μ對CIMGMVC算法性能的影響

如第3章所述，步長μ可在如式（34）所確定的范圍內來取值，本節進一步研究步長對于算法性能的影響。不同步長（0.001、0.004、0.008、0.01、0.05、0.1、0.5）時算法的收斂曲線如圖5所示。

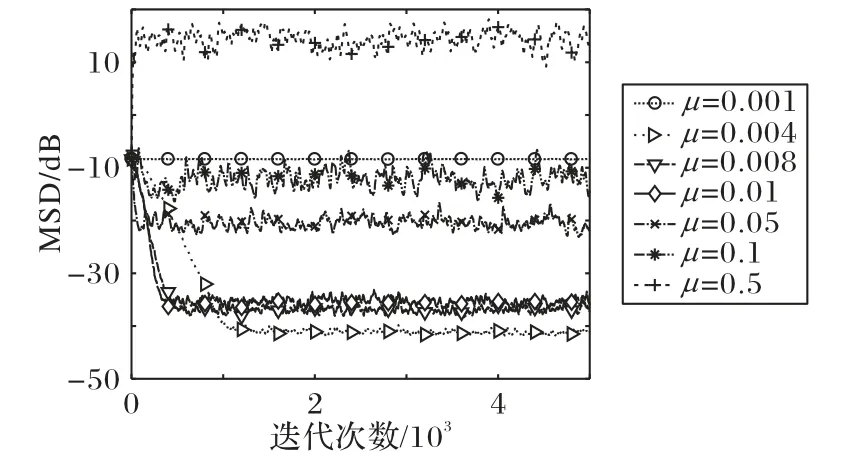
圖5 不同步長μ下的CIMGMVC算法的收斂曲線Fig.5 Convergence curves of CIMGMVC algorithm with different values of step size μ

從圖5 結果中發現當步長μ>0.1 時，其收斂性將很差甚至無法收斂，且μ=0.001 時其性能也很差。而當步長選擇其他值時，雖然具有不同的穩態精度和初始收斂速度，但均可收斂。該結果表明，步長是影響算法性能的關鍵，要保證算法的收斂性，必須選擇合理的步長參數，也即需要使其符合算法收斂分析中給出的步長選擇的范圍式（34）。

5 結語

考慮到非高斯噪聲干擾環境下稀疏系統參數辨識的穩健性，本文提出了基于最大廣義Versoria 準則的稀疏自適應濾波算法——CIMGMVC，該算法充分發揮了廣義Versoria 準則的魯棒性和CIM 的稀疏約束特性，從而有效地克服了非高斯脈沖噪聲對算法性能的影響，獲得了更高的稀疏參數辨識精度。本文也進一步在相關假設下，分析了所提算法的收斂性。實驗結果表明，在不同噪聲能量下，通過設置合適的自由參數可使得辨識結果非常逼近真值，表現出理想的收斂性能。未來可在自由參數p和核寬度的優化方面進行研究，以進一步改進算法的性能。