基于pinball損失的結構模糊多分類支持向量機算法

李 凱，李潔

（河北大學網絡空間安全與計算機學院，河北保定 071002）

0 引言

支持向量機（Support Vector Machine，SVM）是由Vapnik等［1］提出的一種機器學習方法，其目標是根據輸入樣本集求解一個二次規劃問題，從而獲得所需的最優分類超平面。為了解決SVM 計算復雜度高的問題，Jayadeva 等［2］提出了孿生支持向量機（Twin Support Vector Machine，TWSVM），該方法通過求解兩個較小的二次規劃問題，確定兩個非平行的超平面，使得每個超平面更接近其中的一個類而遠離另一個類，該模型較好地提高了計算速度。此后，在TWSVM 的基礎上，研究者們提出了多種孿生支持向量機算法［3-4］，如基于pinball 損失的孿生支持向量機［5-7］、模糊孿生支持向量機［8］和結構型孿生支持向量機［9-10］等，并將其應用于實際問題［11］。

可以看到，上述算法均適用于二分類問題，然而，在實際應用中多分類問題更加常見，因此對多分類問題的研究是十分必要的。目前，人們基于孿生支持向量機對多分類問題［12］進行了研究，主要分為三種類型：

1）第一類是基于二分類的多分類策略。該策略主要包括一對一和一對多兩種：一對一策略是在任意兩類之間構造一個二分類器，對待分類樣本使用投票法進行分類。例如Shao等［13］提出了一對一孿生支持向量機（One-Versus-One TWSVM，OVO-TWSVM）。該方法的缺點是當數據類別較多時，需構造的分類器數量過多，且存在數據不可分區域；而一對多策略［14］是在k個類中任意挑選一類作為正類，其余k-1類作為負類，并構造k個二分類器進行分類，缺點是每個分類器的訓練集高度不平衡；有向無環圖支持向量機（Directed Acyclic Graph TWSVM，DAG-TWSVM）［15］可視為OVOTWSVM方法的一種變形，其訓練過程與OVO-TWSVM 相似，在測試時使用有向無環圖對分類樣本進行分類，有效減少了投票輪數，然而當數據類別較多時仍需構造大量的分類器，且在判決過程中存在誤差累積的現象。Don 等［16］提出了一種分而治之支持向量機（Divide and Conquer SVM，DCSVM），它將OVO-TWSVM 方法的簡潔性與DAG-TWSVM 的分類速度相結合，克服了分類器過多的缺點，但分類過程仍存在誤差累積問題。除此之外，研究人員在這些算法的基礎上提出了多種改進算法，Liu 等［17］提出了一種基于OVO 策略和SVM 算法的改進多分類算法，使用K近鄰法為分類器設置權重，提高分類準確率；Yang 等［18］將多重遞歸投影孿生支持向量機、最小二乘法應用到OVA-TWSVM（One-Versus-All TWSVM）算法中，提出最小二乘遞歸投影孿生支持向量機等。

2）第二類是基于二分類方法演變的其他解決方法，包括一對一對多孿生支持向量機Twin-KSVC（TwinK-class Support Vector Classification）［19］和多生支持向量機（Multiple Birth SVM，MBSVM）［20］。一對一對多孿生支持向量機較好地解決了OVO-TWSVM 中存在的隨機投票現象，但其子分類器復雜，時間復雜度過高；而多生支持向量機極大減少了約束條件，使得時間復雜度低，計算速度顯著提高，但該算法容易陷入局部最優；之后，研究人員針對這些方法提出了許多改進算法［21-24］。

3）第三類是直接構造解決多分類問題的方法。該方法針對所有樣本直接構造一個單一優化問題，并確定所有類的決策函數，該方法有效解決了其他方法中存在不可分區域等問題。例如：Guo 等［25］為解決SVM 不適用于未標記的數據的問題，提出了一種基于主動學習和SVM 多分類模型用于處理未標記的數據。Weston 等［26］提出了多分類支持向量機（Multi-Class SVM，MSVM），但其存在二次規劃問題過大與計算時間長等缺陷。Crammer 等［27］通過引入克羅內克函數，使得約束更加緊湊，但其計算量依然較大。Wang等［28］通過引入新的寬松邊界條件，提出了簡化的多分類支持向量機（Simplified Multi-Class SVM，SimMSVM）算法，較好地提高了計算速度，如圖1（a）所示。然而，由于該方法使用鉸鏈損失，很容易導致算法具有噪聲敏感性和重采樣不穩定性；此外，在一些應用中，例如在推薦系統中，較新產品的重要性程度應高于舊產品，同樣地，不同樣本對支持向量機的作用可能不同；最后，樣本間存在潛在的結構信息，這些信息可能包含一些重要的先驗知識來訓練分類器，該方法未考慮到這幾點，使得該方法對噪聲或異常點仍具有較大的敏感性和較低的泛化性能，分類結果較差。

圖1 兩種算法的分類示意圖Fig.1 Classification schematic diagram of two algorithms

為了進一步解決上述問題，將pinball損失函數、樣本模糊隸屬度和樣本結構信息等引入到SimMSVM 算法中，本文提出了一種基于pinball 損失的結構模糊多分類支持向量機算法Pin-SFSimMSVM。如圖1（b）所示，該方法使用pinball 損失函數對分類錯誤的樣本進行懲罰，同時對分類正確的樣本給出一個額外懲罰，該函數使用分位數距離，使其對噪聲不敏感，數據重采樣更穩定；為樣本添加模糊隸屬度，使得屬于一個類的樣本在分類時扮演更重要的角色；最后，將數據的先驗結構信息應用到算法中，進一步提高了支持向量機的分類性能。

1 相關工作

對SimMSVM 算法的數學模型、算法中用到的鉸鏈損失函數以及本文所提出的Pin-SFSimMSVM 算法所用到的pinball損失函數進行介紹。

1.1 SimMSVM

為了解決多分類問題，Wang等［28］提出了一種新的支持向量機算法，通過最大化每類到其余類的余量來區分出所有類，并且可一次性確定所有類的決策函數，解決了存在不可分區域的問題，且和同類方法相比在速度上也有較大的提升。給定l個樣本的k類數據集T={(x1，y1)，(x2，y2)，…，(xl，yl)}，其中xi∈Rn為訓練數據樣本，yi∈{1，2，…，k}為類標簽，其優化問題如下：

其中：C為懲罰參數；wm為第m類的分類決策向量；H為適當維度的特征空間。通過求解式（1）可以得到所有k個類的分類決策向量。對于待分類樣本x，利用式（2）確定其類別：

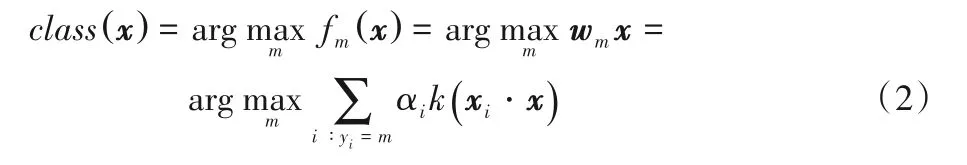
1.2 損失函數

對于支持向量機與孿生支持向量機以及相關算法，在建立相應模型時，主要使用了鉸鏈損失函數，即：

Lhinge(u)=max{0，u}

在算法中，常見的使用形式為：

Lhinge(x，y，f(x))=max(0，1-yf(x))

其中：y和f（x）分別為理想值和預測值。由于鉸鏈損失函數使用了最短距離，因此，它易導致噪聲敏感性和重采樣的不穩定性。為此，人們對不同損失函數的SVM 及TWSVM 進行研究，其中pinball 損失函數研究較為廣泛。pinball 損失函數定義如下：

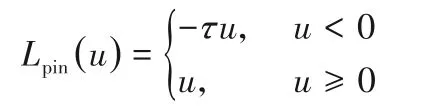
在本文中，使用的pinball損失函數為：

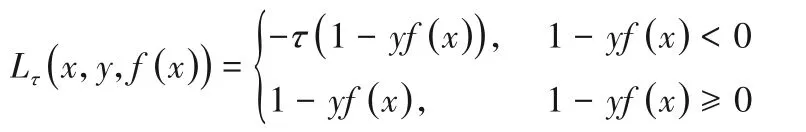
其中τ∈［0，1］?？梢钥吹?，pinball損失函數不僅對分類錯誤的樣本進行懲罰，而且對分類正確的樣本給出一個額外懲罰；另外，由于該函數使用了分位數距離，因此，它對噪聲不敏感，數據重采樣更穩定，且不會增加計算成本。當pinball 損失的參數趨于零時，損失函數成為鉸鏈損失。

2 結構模糊多分類支持向量機

在本章中，將pinball損失函數、樣本權重和樣本的結構信息引入到SimMSVM 中，提出了一種新的多分類支持向量機算法Pin-SFSimMSVM。使用pinball 損失函數能較好地解決鉸鏈損失函數所帶來的噪聲敏感和重采樣不穩定性等問題，通過引入模糊隸屬度對樣本賦予不同權重，并充分挖掘樣本中潛在的結構信息，數據中可能包含用于訓練分類器的重要先驗知識，進一步提高了算法的噪聲不敏感性和算法的性能。該方法不僅保留了SimMSVM 中一次性解決所有樣本的分類問題、避免產生數據不可分區域和計算速度快等優點，且提高了算法的抗噪性和分類準確率。下面將從線性和非線性兩種情況對算法進行介紹。

2.1 線性情況

給定一個含有l個樣本的k類訓練數據集T={(xi，yi，Si)|i=1，2，…，l}，其中xi∈Rn為訓練樣本，yi∈{1，2，…，k}為樣本類標簽。將pinball 損失函數、樣本模糊隸屬度和樣本結構信息引入到SimMSVM 中，從而得到線性Pin-SFSimMSVM的優化問題：

其中：wm為第m類樣本的分類決策向量；C1和C2分別是平衡因子且C1>0，C2>0；Si為樣本模糊隸屬度；ξi為松弛變量；Σm為第m類樣本的結構信息；τ∈［0，1］為pinball損失參數。為了解決式（3），構造拉格朗日函數如下：

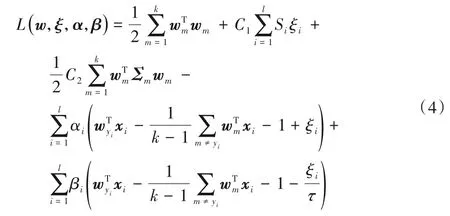
其中α和β是由拉格朗日乘子構成的向量，且α≥0，β≥0。

將拉格朗日函數對變量求偏導并令其等于0，得：

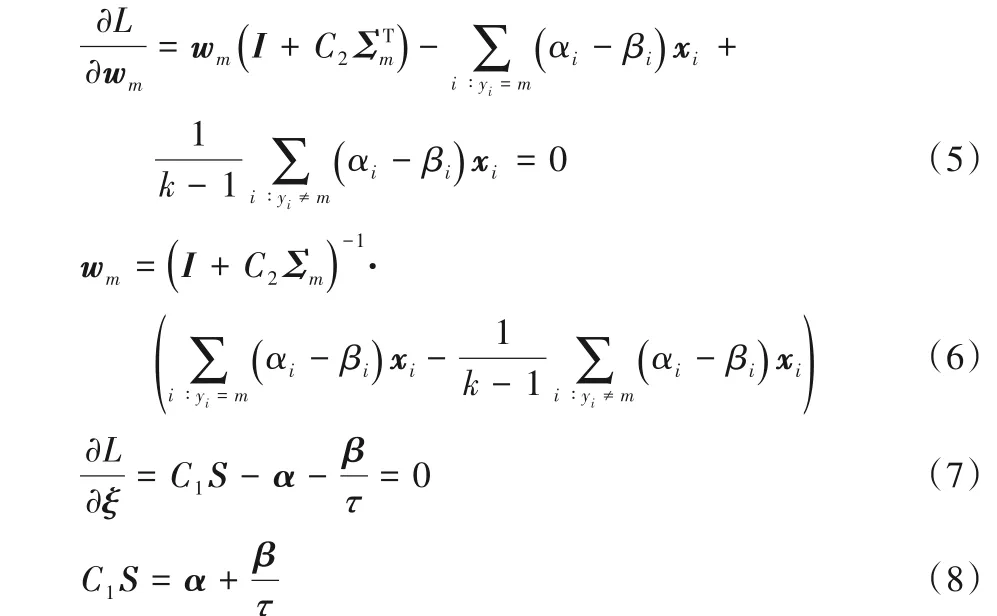
由式（7）和式（9）可得約束條件為：

將式（6）和式（8）代入到式（4）中，從而得到式（3）的對偶問題如下：

其中：γ=(α-β)；S為由樣本模糊隸屬度構成的向量；G為一個l×l維的矩陣。G的矩陣元素為：

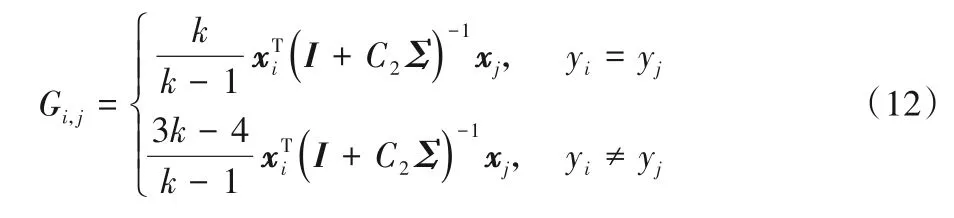
其中I為適當維度的單位矩陣。

通過求解對偶問題式（11），從而得到γ，進一步可以求得wm，即每類樣本的分類決策向量。因此，獲得的決策函數為：

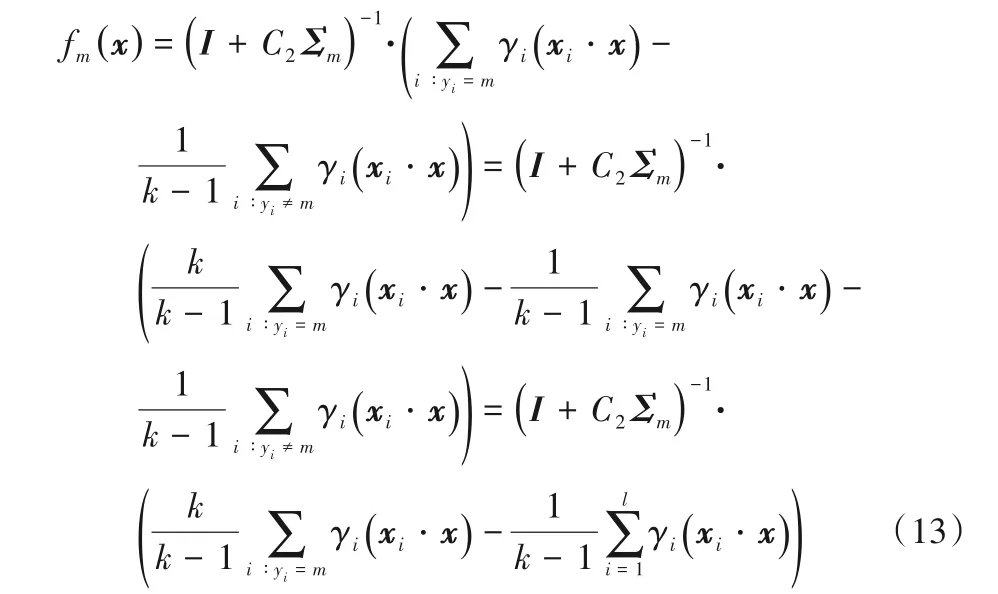
當對待分類樣本x進行分類時，其最終所屬類別的求解方法如下：

2.2 非線性情況

在這一節中，將線性情況推廣到非線性情況中。通過核矩陣將輸入樣本映射到高維特征空間，使其在高維空間中也能實現線性可分。設φ是一個從輸入空間Rn到特征空間Z的映射，則非線性Pin-SFSimMSVM算法的優化問題為：

其中：um為第m類樣本的分類決策向量：C3、C4是平衡因子且C3>0，C4>0；ξi、Si和Σm分別為松弛變量、樣本模糊隸屬度和第m類樣本的結構信息，τ∈［0，1］為pinball損失參數。其拉格朗日函數為：

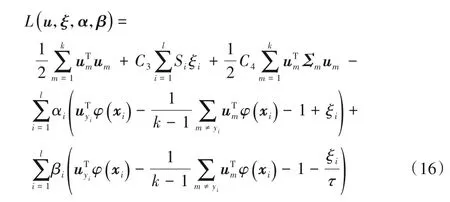
其中α≥0，β≥0為拉格朗日乘子。

將式（16）對變量求偏導并令其等于0得：

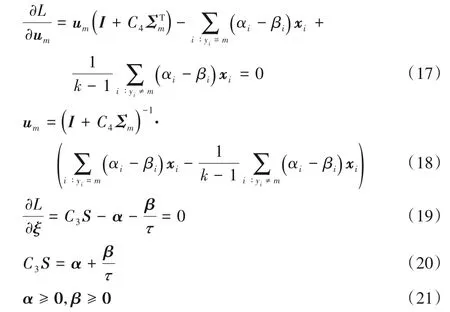
由式（19）和式（21）可得約束條件為：

將式（18）、（20）代入式（16），從而得到式（15）的對偶問題為：

其中：γ=(α-β)；S為由樣本模糊隸屬度構成的向量；G為一個l×l維的矩陣。G的元素為：

其中I為適當維度的單位矩陣。

通過對其對偶問題進行求解，求得um的值，進而得到如下決策函數：

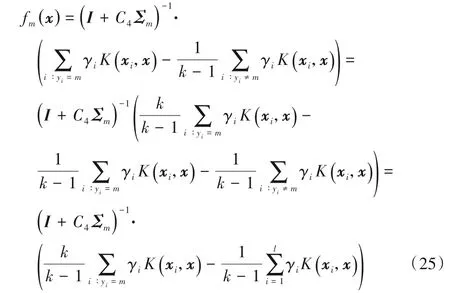
其中K(xi，x)=φ(xi)Tφ(x)。

對于待分類樣本x，利用決策函數可確定樣本x所屬類別，即：

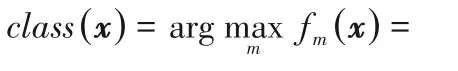
2.3 時間復雜度分析

對Pin-SFSimMSVM 算法的時間復雜度進行分析，該方法針對所有樣本直接構造一個單一優化問題，一次性確定所有類的決策函數，并采用了較為簡單的損失函數，因此時間復雜度為O(l3)，其中l為問題的規模。

3 實驗與結果分析

首先，對樣本模糊隸屬度以及樣本結構信息的獲取方法進行介紹，實驗中采用類中心距離法、模糊C 均值法和S 型方法獲取樣本模糊隸屬度，并分別使用基于距離和基于聚類的方法獲取樣本結構信息。接著，對提出的Pin-SFSimMSVM 算法的性能進行評估，從線性和非線性兩種情況對算法進行實驗比較。將SimMSVM［28］、OVO-TWSVM［13］、OVA-TWSVM［14］、Twin-KSVC［19］以及MBSVM［20］等多種多分類算法與所提出的Pin-SFSimMSVM 算法在UCI 數據庫［29］中的8 個標準數據集和4 個人工生成的數據集上分別進行實驗。此外，在標準數據集中分別加入5%和10%的特征噪聲并比較其準確率，以檢驗算法對噪聲的敏感性。結果表明，Pin-SFSimMSVM 算法在標準數據集和人工生成的數據集中都有很好的抗噪性。

3.1 模糊隸屬度

為了研究不同樣本賦予不同權重時對分類結果的影響，本文將對使用類中心距離法、模糊C 均值法和S 型三種不同方法賦予權重值時的測試結果進行比較。

1）類中心距離法。該方法根據每類中的樣本距離該類中心的距離遠近來定義其權重，距離類中心點越近的樣本權重越大，距離越遠權重越小。計算k類中的任意一類中的樣本權重Si的方法如下：

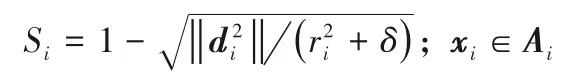
其中：di表示該樣本到該類類中心的距離；ri表示該類的半徑，即距離類中心最遠的樣本到中心的距離。

2）模糊C 均值法。該方法將每類樣本分為C個簇并使每個樣本到C個聚類中心的距離最小，即為每一個樣本賦予一個權重，該權重的值表示樣本隸屬于某一簇的重要程度。任意一類的優化問題如下：

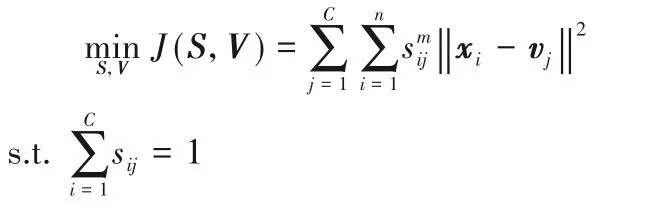
其中：vj為聚類中心；sij為第i個樣本在第j個簇中的權重；V和S分別由vj和sij組成；m為模糊加權指數。通過拉格朗日求解該優化問題得到vj和sij的計算式，再通過求解公式迭代更新矩陣S和集合V：

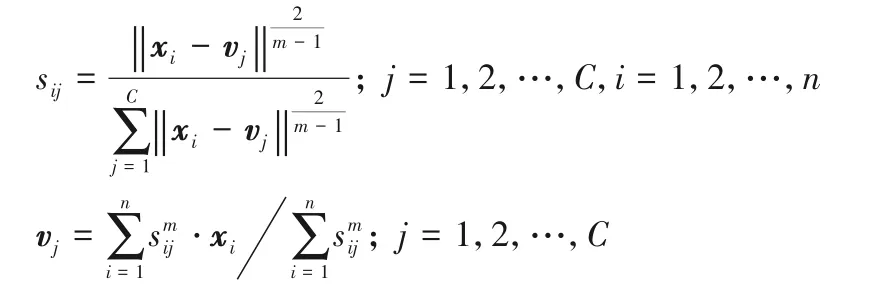
3）S 型方法。與類中心距離法相似，根據樣本點距離該類中心的距離遠近來確定權重，不同的是，該方法將類中心距離法中的線性函數用如下非線性函數替換：

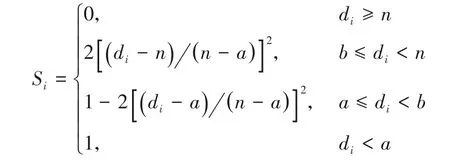
其中：a、b、n均為定義好的參數并滿足b=(a+n)/2，且當di=b時，Si=0.5。

3.2 結構信息

同樣在算法中加入樣本的結構信息可以更好地利用數據樣本中潛在的分布信息，本文主要使用以下兩種方法來獲取結構細信息。

1）類內離散度法求結構信息：用于描述每個類內部的結構信息。設μm為第m類樣本的均值向量，nm表示第m類樣本的個數，則結構信息可表示為：

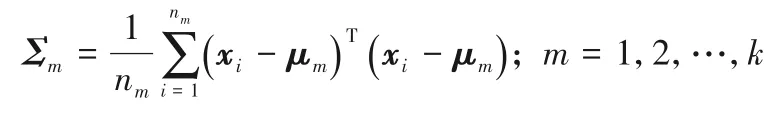
2）基于聚類方法求結構信息：該方法通過對每類樣本進行聚類，將其劃分成不同的簇，計算出每個簇的聚類信息再求和得到該類的聚類信息。本文中主要使用到的聚類技術有模糊C 均值聚類、層次聚類和C 均值聚類。假設將其中第m類樣本聚類成c個簇，則第i個聚類簇和第m類的結構信息可分別表示為：

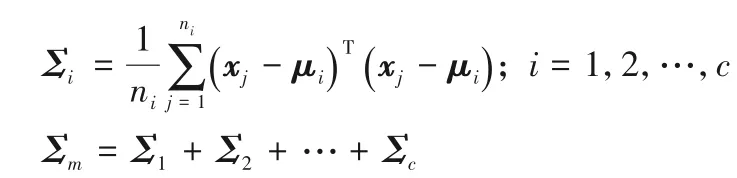
3.3 實驗數據集和分類性能評價指標

實驗選取Ripley 綜合數據集［30］、人工生成的3 個數據集和UCI 標準數據庫中的8 個數據集對Pin-SFSimMSVM 算法進行驗證。其中Ripley 為二類數據集，共包含250 個訓練樣本和1000個測試樣本，人工數據集中的數據為正態分布下隨機生成得到，將其分別命名為Data1、Data2 和Data3。其中，Data1每個類數據按照均值[-5，5]、[5，5]、[-5，-5]和[5，-5]，方差［0.40；03］生成。Data2 中共三個類：第一類包含3 個簇，每個聚類簇按照均值[2，-2]、［0，2］和[-4，5]，方差［0.70；00.7］生成；第二類包含2 個簇，每個聚類簇按照均值[-5，1]和[-1，0]，方差［0.40；03］生成；第三類包含3 個簇，每個聚類簇按照均值[-5，-4]、[-2，-4]和[1，-4]，方差［1.50；00.7］生成。Data3每個類數據則按照均值[-4，4，2]、［4，4，2］、[-4，-4，2]、[4，-4，2]和［0，0，2］，方差［200；020；003］生成。數據集中的樣本數、特征個數、分類數目和每類樣本所包含的簇數如表1所示。

表1 人工數據集特征Tab.1 Synthetic dataset characteristics

選用UCI 數據庫中的8 個標準數據集對算法進行驗證，它們分別為Iris、Zoo、Glass、Seeds、Ecoli、Balance、Soybean 和CMC，表2中描述了數據集的詳細特征。

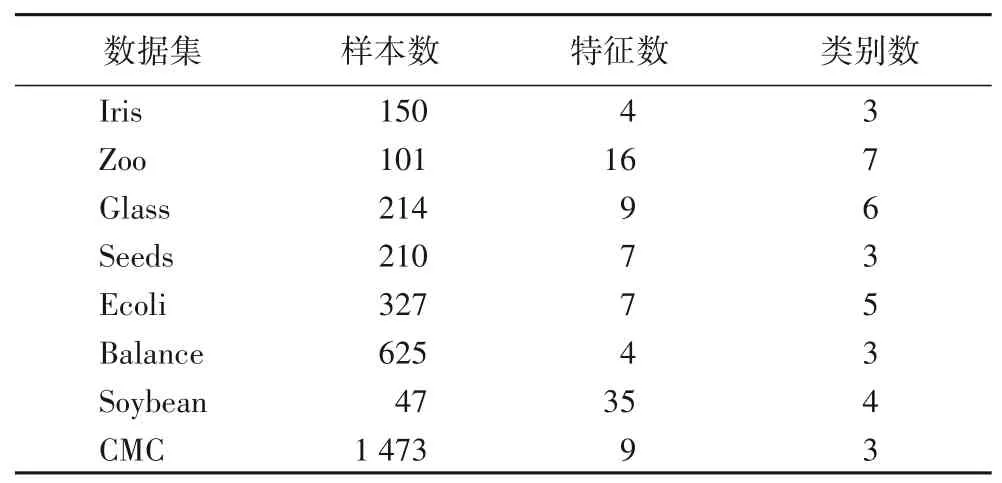
表2 UCI數據集特征Tab.2 UCI dataset characteristics

另外，在分類問題中，分類器的性能評價指標也是選擇最優分類器的重要依據。本文中選取的評價指標為分類準確率和標準差，準確率為分類正確的樣本與總樣本的比，標準差則是算法在數據集上進行10 次分類結果平均值方差的平方根。

3.4 Pin-SFSimMSVM算法實驗

將所提出的算法Pin-SFSimMSVM在人工數據集和UCI標準數據集上進行實驗，并與SimMSVM、OVO-TWSVM、OVATWSVM、Twin-KSVC 以及MBSVM 這幾種常用的多分類算法進行對比。下面介紹實驗中用到的參數及參數的選擇。懲罰參數C1和C2為平衡因子且大于0，C1值較大時對誤分類的懲罰增大，C2值較大時則結構信息所起作用增大；反之亦然。在非線性情況下，使用高斯核函數k(x，y)=作為核函數。當pinball 損失參數τ為0 時，損失函數為鉸鏈損失，因此參數τ在（0，1］取值。為使實驗結果達到最優，C1，C2和p在2-4～210進行取值，首先取80%的樣本為訓練數據集，使用網格搜索和十重交叉驗證的方法對4 個參數進行篩選，得到實驗結果最優時的各項參數值；并使用得到的最優參數對訓練數據進行訓練得到決策函數，對測試樣本進行分類得到最終的分類準確率。實驗中對每種算法均采用10 次測試的平均值和標準差作為最終的評價指標。

為驗證所提出算法的分類性能，在表3和表4中分別給出了線性及非線性情況下，已有的5 種用于多分類的算法和本文所提出的Pin-SFSimMSVM 算法在幾個人工數據集上的分類準確率和標準差。其中Pin-SFSimMSVM算法使用模糊C均值法獲取樣本模糊隸屬度，并分別使用層次聚類和C 均值聚類方法獲取樣本的結構信息。

根據表3和表4可以看出，Pin-SFSimMSVM算法在線性和非線性情況中均表現出比SimMSVM 算法更好的性能，且在Ripley、Data1和Data2這3個數據集中均優于其余幾種多分類算法。SimMSVM 和Pin-SFSimMSVM 這兩種算法對Ripley 數據集和Data1數據集的一次分類結果如圖2～3所示，在圖中對分類錯誤的樣本點進行了標記。

圖2 Ripley數據集及使用不同算法在其上的分類結果Fig.2 Ripley dataset and classification results of different algorithms on it

表3 線性情況下不同算法準確率和標準差對比 單位：%Tab.3 Comparison of accuracy and standard deviation of different algorithms in linear condition unit：%

表4 非線性情況下不同算法準確率和標準差比較 單位：%Tab.4 Comparison of accuracy and standard deviation of algorithms in nonlinear condition unit：%

在UCI 數據集上的部分實驗結果如表5～6 所示，對每個數據集中實驗結果最好的算法進行了標記，其中Pin-SimMSVM 算法為僅使用pinball 損失替換原算法中的鉸鏈損失而不作其他改變得到的算法，和原算法進行對比可以更好地觀察不同損失函數對算法分類結果的影響?？梢钥闯?，大多數數據集在使用pinball 損失和模糊隸屬度后，準確率已有了一定的提升，為了研究pinball 損失參數τ 的變化對分類結果的影響，使用非線性情況下的Pin-SimMSVM 算法對其進行測試，在圖4 中給出了在UCI 數據集上Pin-SimMSVM 算法的精度隨pinball 損失參數τ 變化的規律，可以看出，隨著τ 值的變化，數據集的準確率十分穩定，表明了Pin-SimMSVM 算法的性能是穩定的。

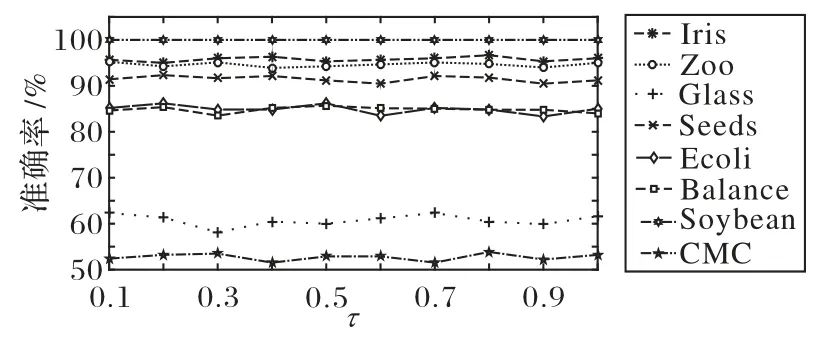
圖4 UCI數據集上Pin-SimMSVM算法的精度隨τ值變化曲線Fig.4 Accuracy curve of Pin-SimMSVM algorithm varying with τ on UCI datasets

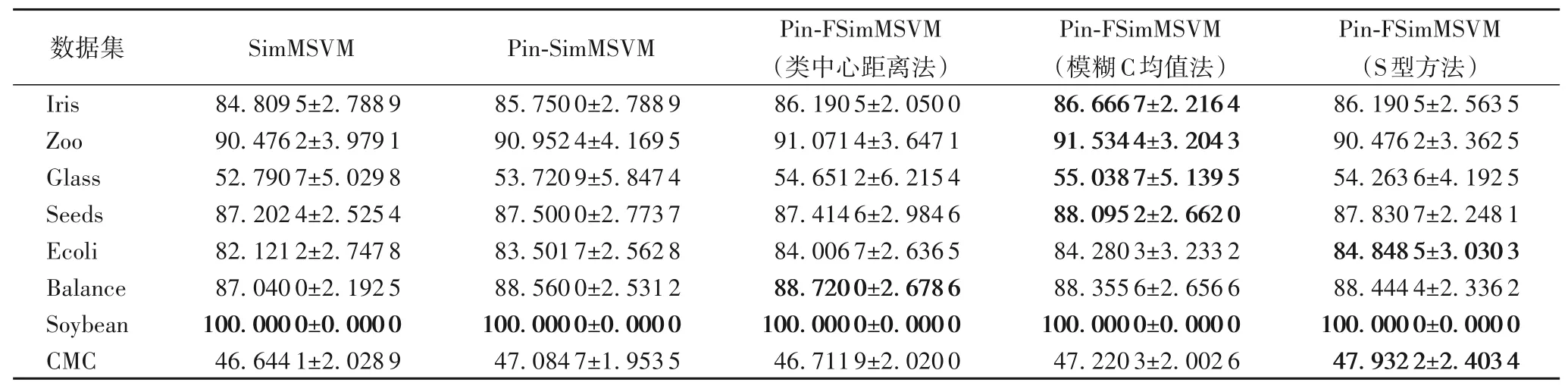
表5 不同算法求取模糊隸屬度在UCI數據集上的準確率和標準差對比（線性） 單位：%Tab.5 Comparison of accuracy and standard deviation of different algorithms in solving fuzzy membership degree on UCI datasets（linear）unit：%

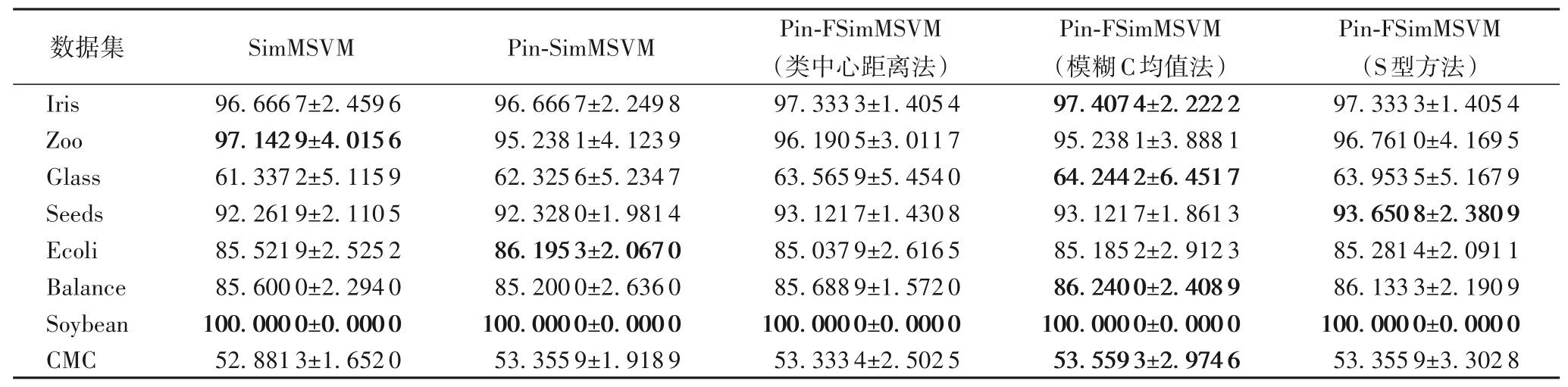
表6 不同算法求取模糊隸屬度在UCI數據集上的準確率和標準差對比（非線性） 單位：%Tab.6 Comparison of accuracy and standard deviation of different algorithms in solving fuzzy membership degree on UCI datasets（nonlinear）unit：%

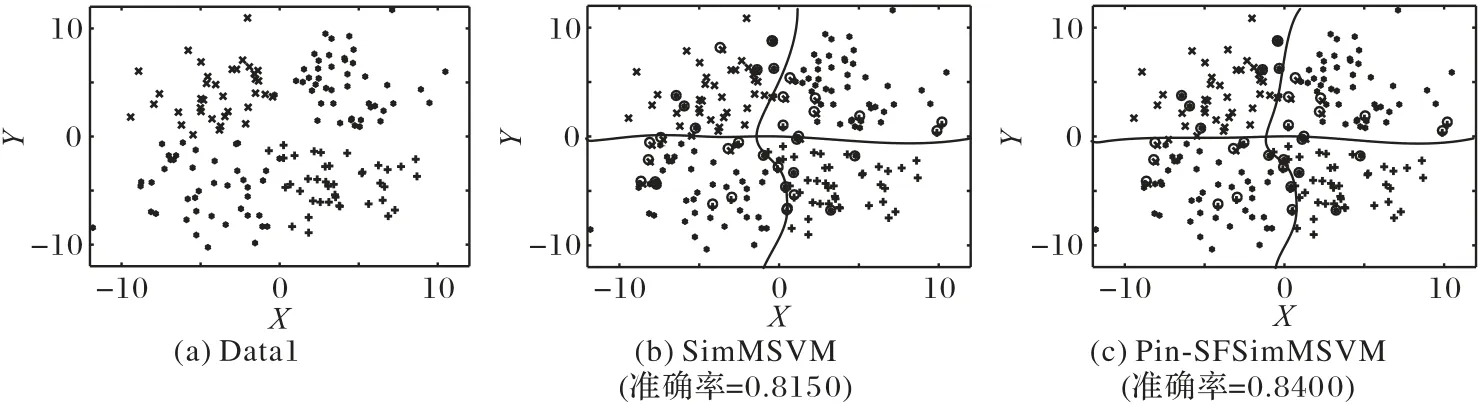
圖3 Data1數據集及使用不同算法在其上的分類結果Fig.3 Data1 dataset and classification results of different algorithms on it

為驗證不同獲取樣本模糊隸屬度的方法對實驗結果的影響，使用在Pin-SimMSVM 算法的基礎上引入樣本模糊隸屬度得到的Pin-FSimMSVM 算法進行實驗，分別使用類中心距離、模糊C 均值和S型三種方法獲取樣本模糊隸屬度，根據表5～6的實驗結果可以看出，使用模糊C 均值方法獲取模糊隸屬度的算法在大部分數據集中具有較好的性能：線性情況下在Ecoli、Balance和CMC三個數據集中略低于其他獲取模糊隸屬度的方法，但相較于SimMSVM算法依然具有優勢；非線性情況下，模糊C均值方法和S型方法均具有較好的性能。因此，在后續實驗中均選取模糊C均值方法獲取樣本模糊隸屬度。

除此之外，針對選取的UCI 數據集，表7～8 中給出了線性及非線性情況下，使用四種不同獲取樣本結構信息的算法準確率，根據結果可知，與基于距離的方法比較，基于聚類的方法具有一定的優勢，特別是層次聚類其優勢較為明顯。

表7 不同算法求取結構信息在UCI數據集上的準確率和標準差對比（線性） 單位：%Tab.7 Comparison of accuracy and standard deviation of different algorithms in solving structural information on UCI datasets（linear）unit：%

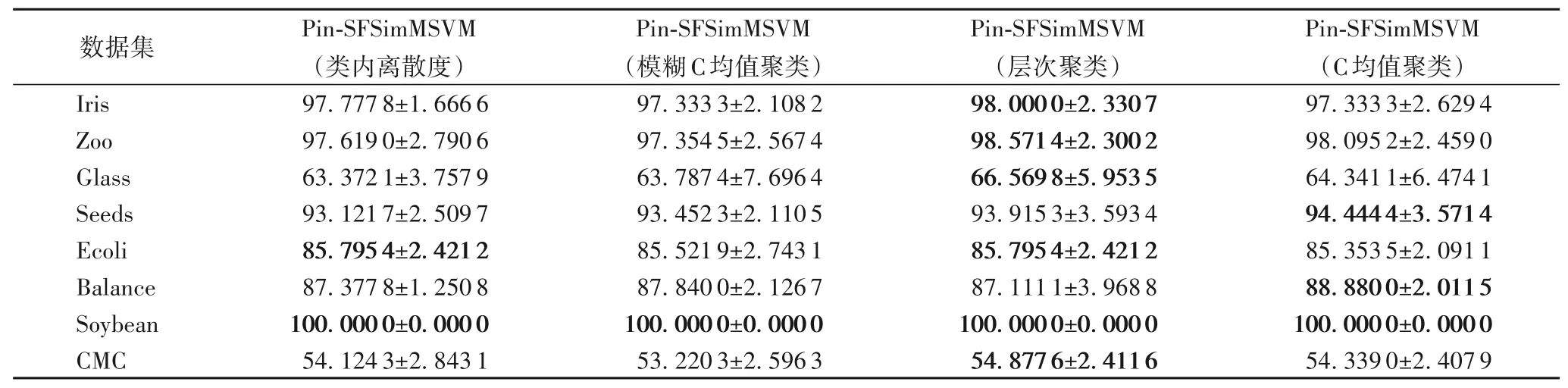
表8 不同算法求取結構信息在UCI數據集上的準確率和標準差對比（非線性） 單位：%Tab.8 Comparison of accuracy and standard deviation of different algorithms in solving structural information on UCI datasets（nonlinear）unit：%

為了驗證所提出的Pin-SFSimMSVM 算法的有效性，在標準數據集上進行實驗并選取SimMSVM、OVO-TWSVM、OVATWSVM、Twin-KSVC 與MBSVM 算法進行比較；同時，為了檢驗算法的抗噪性能，在8 個標準數據集中分別加入了5%和10%的噪聲數據進行對比實驗，噪聲數據服從均值為0、方差為1 的高斯分布，實驗結果見表9，其中r表示所含噪聲比例，結構信息的獲取分別使用層次聚類和C均值聚類方法。

表9 不同算法在UCI數據集上添加噪聲的準確率和標準差對比（非線性） 單位：%Tab.9 Comparison of accuracy and standard deviation of different algorithms on UCI datasets with adding noise（nonlinear） unit：%

實驗結果表明，在選取的8 個UCI 標準數據集中，Pin-SFSimMSVM 算法在7 個數據集中均表現出優異的性能，尤其是在加入噪聲數據后，準確率均高于其他算法，而在Balance數據集中，盡管本文所提出的算法低于OVO-TWSVM 等算法，但仍優于SimMSVM 算法，且在加入噪聲后得到的實驗結果仍有明顯提高，這也表明了所提出的算法對噪聲和重采樣數據不具有敏感性。

此外，根據表9的實驗結果，將Pin-SFSimMSVM 算法的實驗結果與其他五種多分類算法的實驗結果在8 個標準數據集中進行比較，如表10所示。其含義為將Pin-SFSimMSVM 算法與其他五種不同算法在UCI 標準數據集上的輸局/平局/贏局個數，例如Pin-SFSimMSVM 算法與SimMSVM 算法在沒有添加噪聲情況下相比較的結果為1/1/6，則表明所提出的算法僅1次準確率低于原算法，1次準確率與原算法相等，6次結果優于原算法。

表10 Pin-SFSimMSVM算法與其他算法在UCI標準數據集上的贏局/平局/輸局對比Tab.10 Comparison of Pin-SFSimMSVM algorithm with other different algorithms for win/draw/loss on UCI standard datasets

可以發現，本文所提出的算法的性能僅在一個數據集上差于改進前的SimMSVM 算法，但在噪聲數據集上優于SimMSVM 算法，與其他算法相比，所提出的算法也具有很高的精度，表明Pin-SFSimMSVM具有更好的噪聲不敏感性。

4 結語

本文提出了一種新的用于多分類的支持向量機算法Pin-SFSimMSVM，該算法在SimMSVM 的基礎上，基于pinball 損失函數，通過引入樣本的模糊隸屬度和結構信息，較好地解決了多分類方法存在不可分區域，以及對數據中的噪聲和重采樣數據敏感等問題，并且在準確率上有很大提升。通過在人工數據集和UCI 標準數據集上對SimMSVM、OVO-TWSVM、OVA-TWSVM、Twin-KSVC 以及MBSVM 等多分類算法的對比實驗，驗證了所提出算法的有效性。