基于歷史事故數據的液化天然氣工廠設備風險事故預測研究

程松民

昆侖能源湖北黃岡液化天然氣有限公司

我國液化天然氣工廠的數量不斷增加，一方面由于液化天然氣工廠內設備的數量及類型相對較多，運行工藝相對較為復雜，在設備運行的過程中可能會出現各種類型的風險事故[1]。另一方面，液化天然氣本身就屬于一種易燃、易爆物質，如果設備運行出現風險事故，可能會引發更大的風險問題，由此可見，保障液化天然氣工廠內設備的運行安全十分關鍵[2-4]。保障設備運行安全的前提是及時對風險事故進行預測，以便制定安全保障方案和風險預案。因此，對液化天然氣工廠內的設備運行風險事故進行全面的預測研究十分重要。

目前，國內外學者對液化天然氣工廠內設備運行安全問題進行了廣泛的研究。田宇忠等[5]在綜合考慮多米諾效應的基礎上，對液化天然氣工廠出現風險事故以后的后果進行了全面的研究，并對風險事故以后設備的損壞概率以及人員傷亡進行了全面的計算，研究結果表明，考慮多米諾效應前提下的風險定量評價結果更加的準確；王志寰等[6]對液化天然氣工廠內設備泄漏風險問題進行了全面的研究，在研究的過程中，充分考慮了液化天然氣工廠所處的地理位置，根據實際布置狀況建立了三維預測模型，對泄漏風險問題進行了全面的預測，研究結果表明，所建立的三維預測模型相對較為準確，可用于液化天然氣工廠泄漏風險預測及分析；HAMEED 等[7]建立了一種基于風險雙目標的模型，對液化天然氣工廠內的脫硫裝置運行風險問題進行了全面研究，該模型可以為制定脫硫裝置的維修決策提供指導建議。

通過對國內外研究現狀進行分析可以發現，目前國內外的研究主要集中在單一設備的運行風險或者風險事故的危害評價方面，對于整個液化天然氣工廠內設備風險事故的預測研究相對較少。為此，本次研究主要是引入了差分自回歸移動平均（ARIMA）、最小二乘支持向量機（LS-SVM）以及BP神經網絡（BPNN）三種類型的算法，提出了三種算法的組合方式，利用組合模型對液化天然氣工廠內設備的運行風險事故進行了預測研究，可以為了解液化天然氣工廠內設備風險事故的變化趨勢以及制定安全保障措施提供指導建議。

1 風險事故預測難點分析

對液化天然氣工廠內的設備風險事故進行預測的難度相對較大，其主要的原因有兩點。首先，液化天然氣工廠內的設備數量以及類型相對較多，液化天然氣工廠主要進行原料氣的凈化、壓縮、天然氣的液化、儲存等工作，其主要的設備裝置包括凈化裝置、分離器、分餾塔、壓縮機、換熱器等[8-9]。在開展日常工作的過程中，各種類型的設備裝置都可能會出現風險問題，且每種類型設備裝置出現的風險事故問題各不相同，引起事故問題的原因也存在眾多的差別，所引發的后果也存在較大的差距，這使得對風險事故進行預測的難度相對較大[10-11]；其次，液化天然氣工廠內的生產工藝相對較為復雜，各種類型的設備串聯在一起，如果一種類型的設備出現風險問題，很可能會引發其他設備的風險問題，因此對液化天然氣工廠內的設備風險事故進行整體性預測的難度相對較大。

針對液化天然氣工廠內設備風險事故預測難度相對較大的問題，本次研究首先將設備的風險事故分為兩種類型，分別是嚴重事故和一般事故（嚴重事故是指會造成人員傷亡和巨大經濟損失的風險事故，一般事故是指會影響生產作業效率和經濟損失較小的風險事故），所有設備的風險事故都將歸結到這兩種類型的事故中，然后對液化天然氣工廠內的設備風險事故進行統一的預測研究。

2 數據來源及研究方法

2.1 某企業風險事故數據

本次研究所使用的數據來源于我國某液化天然氣企業，該企業于2020 年發布了2008—2019 年的運營數據，運營數據中包含了設備運行風險事故類型、出現的原因以及所造成的危害。首先對所有的設備運行風險事故進行了統一的分類，將其分為嚴重風險事故和一般風險事故兩種類型，對這兩種類型的風險事故進行預測研究。該液化天然氣工廠每季度都會針對不同的設備進行維護及檢測，其2008—2019 年的風險事故情況見表1，2008—2019年設備維修情況見表2。

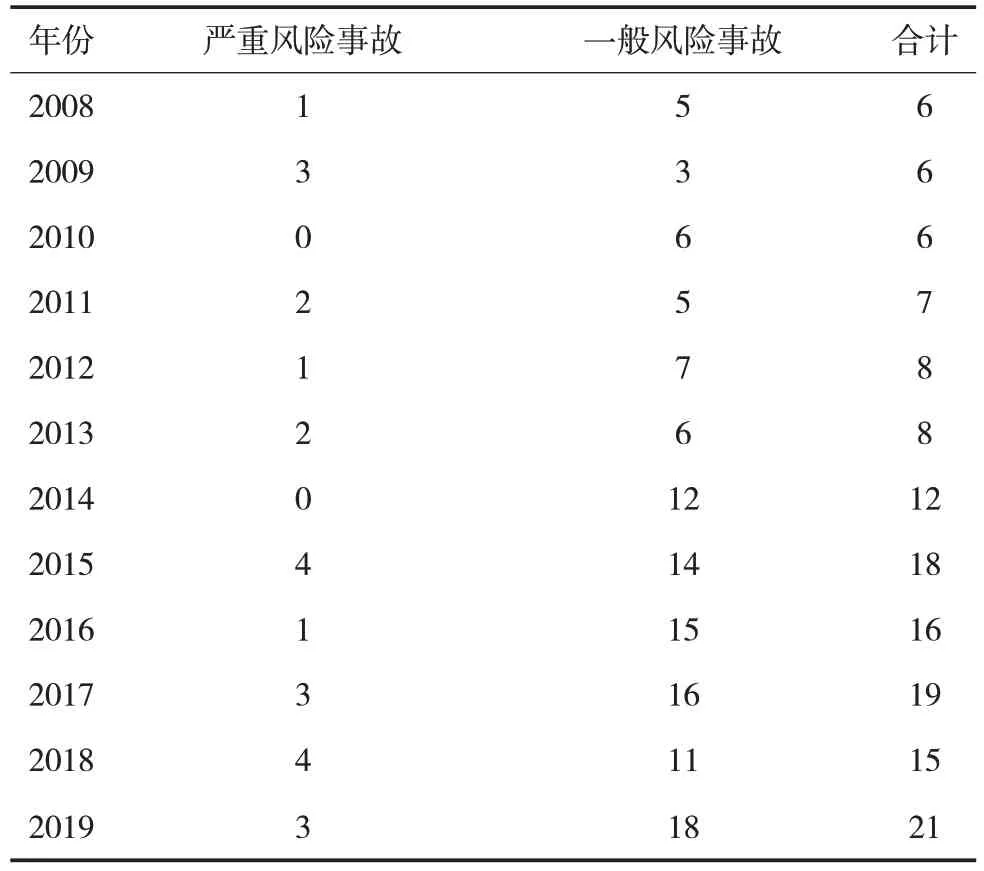
表1 2008—2019年某液化天然氣企業設備風險事故情況Tab.1 Equipment risk accidents of a LNG enterprise from 2008 to 2019

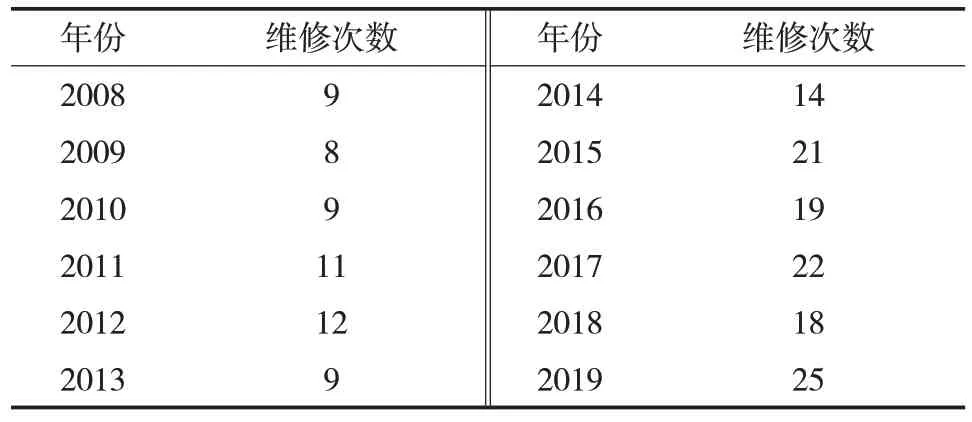
表2 2008—2019年某液化天然氣企業設備維修情況Tab.2 Equipment maintenance times of a LNG enterprise from 2008 to 2019

2.2 模型理論基礎

2.2.1 ARIMA模型

ARIMA 模型主要是通過將時間序列轉化為隨機序列進而對預測值進行全面的預測，該種類型算法模型的精度相對較高[12]。如果某一項數據具有季節性以及趨勢性的基本特征，則可以使用該種模型將其表示為ARIMA(p,d,q)(P，D，Q)s季節模型，在該模型中共含有7項參數，其中p、q為自相關或者偏自相關的函數的階數，d為該模型的差分次數，P、Q、D為季節性中的自相關、偏自相關函數的階數以及函數的差分次數，s為周期[13]。這種模型可以表示為

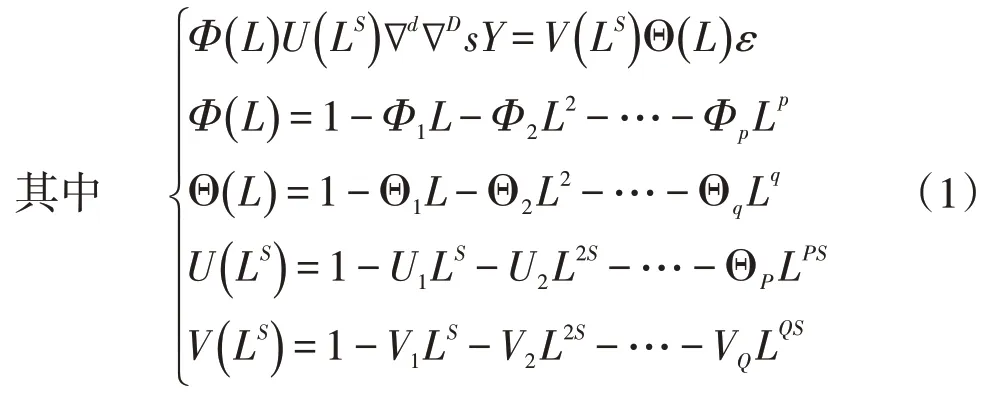
式中：ε為隨機誤差；Φ(L)?dY為在同一個周期之內不同周期點位置處的相關性；U(LS)?Ds為在不同的周期之內相同周期點位置處的相關性。

在進行建模的過程中，首先需要對數據進行差分處理，然后對其進行周期性的觀察，確定d的數值。例如在進行n階的差分處理以后，其周期性已經消失了，此時就可以得到d=n；同時，通過差分的方式也可以確定D的數值。p和q的取值主要可以通過進行差分處理以后的ACF圖以及PACF圖進行確定，P和Q的數值一般都屬于低階情況，因此可以使用從低階向高階嘗試的方法進行確定，在進行確定的過程中可以使用Ljung-Box 的方法進行檢驗，從而確定出最佳的模型。

2.2.2 LS-SVM模型

LS-SVM模型主要是在對SVM模型進行全面優化的基礎上提出的一種算法模型[14]。該種模型可以通過對線性方程組進行全面求解的方式，進而對問題進行一定的簡化，通過該種方式可以使得模型的計算效率得到提升[15-16]。同時，在構建模型的過程中需要一定量的數據，將數據轉化到高維的空間之中進行回歸處理，引入核函數避免出現維度災難問題。非線性的支持向量機可以通過以下方式進行求解

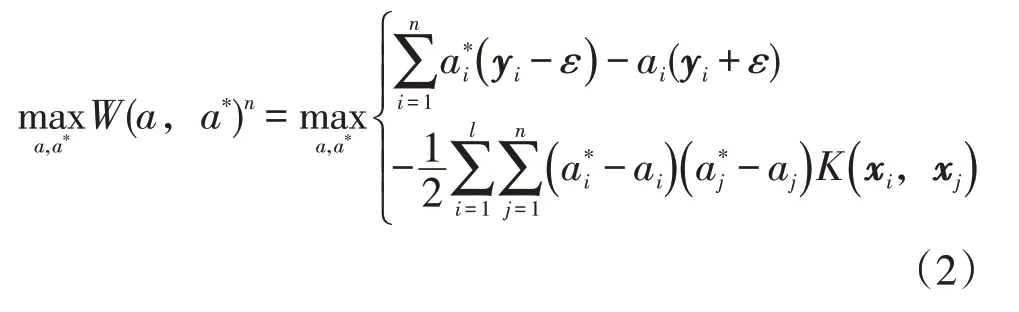
式中：W為擬合函數；yi為第i個輸出向量；xi為第i個輸入向量；i、j為向量序號；ε為殘差；n為輸出向量的數量；l為輸入向量的數量。

上述方程的約束條件為

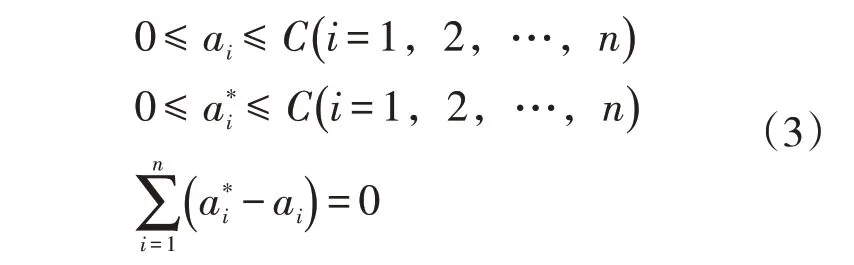
式中：C為正則化參數。

在得到拉格朗日系數αi、以后，該函數f(x)可以表示為

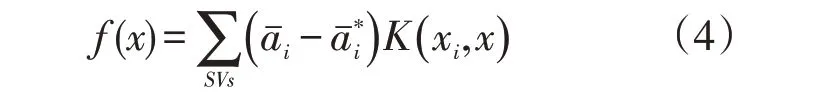
式中：SVs為訓練樣本的空間；K(xi,x)為核函數。

2.2.3 BP神經網絡模型

BP 神經網絡算法屬于一種常見的預測類算法，在使用該種算法的過程中，工作將會正向傳遞，誤差將會反向傳遞[17-18]。在BP神經網絡算法之中，每個樣本數據都會有m個輸入，同時還會有n個輸出，在輸入層I與輸出層O之間還含有隱含層H，其主要是驗證相對誤差平方和最小的方向，對閾值進行反復的修正，進而使得模型的預測誤差達到最低[19]。其誤差函數可以表示為

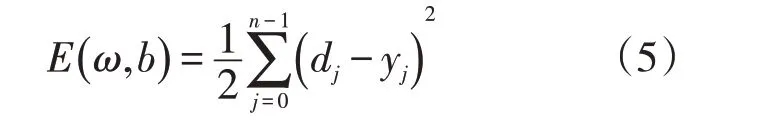
式中：E為誤差函數；ω為權重；b為閾值；n為輸出數據的數量；j為某項數據；dj為模型的輸出結果；yj為數據的真實數值。

2.3 組合模型構建步驟

組合模型的構建分為以下步驟：

（1）首先建立ARIMA 模型，并將液化天然氣企業相關指標數據輸入其中，然后對統計量和顯著性進行一定的擬合，最終得到最佳的模型Y1=f(x)。

（2）然后建立LS-SVM模型，通過使用交叉驗證的方式得到模型的參數，即Y2=s(x)。

（3）使用相關數據對BP 神經網絡模型進行全面的訓練，最終得到模型的參數，即Y3=n(x)。

（4）根據DS 證據理論，對各個模型的權重ai進行確定，最終得到用于液化天然氣工廠設備風險事故預測的模型Y=a1Y1+a2Y2+a3Y3[20-21]。

2.4 自變量篩選

對于液化天然氣工廠設備運行安全而言，其影響因素相對較多，包括設備的運行時間、利用率以及工作人員技術水平等，在對液化天然氣企業進行設備風險預測的過程中，雖然需要建立時間序列模型，但是也必須考慮這些影響因素對模型脆弱性的影響，設備運行風險的脆弱性主要來源于工作人員以及外界環境，本次研究所考慮的設備風險影響因素主要有7 項：①設備運行時間x1；②設備年限x2；③設備利用率x3；④工作人員工作年限x4；⑤工作人員數量x5；⑥惡劣天氣（雷雨、大風出現的天數）狀況x6；⑦經濟效益x7。

3 應用實例分析

3.1 數據預處理

本次研究主要以我國某大型液化天然氣工廠為例，其運行時間已經超過10 年，該工廠內設備風險事故的時序圖如圖1所示。通過對時序圖進行分析可以發現，設備出現風險事故的次數具有較大的波動，且隨著時間的變化，風險事故的次數逐漸升高。其中2008—2012 年該工廠設備出現風險事故的次數相對較少，2013 年以后出現設備風險事故的次數呈現出波動式增加。在進行建模的過程中，將該工廠2008-2017 年的數據作為模型的訓練樣本，對2018 年、2019 年的數據進行預測。為了對季節性因素進行分解，提高數據的穩定性，對數據進行分解，分解結果如圖2所示。通過對分解以后的季節性時序圖進行分析可以發現，該工廠內設備風險事故也呈現出了明顯的季節性特征，由此可確定s=12。

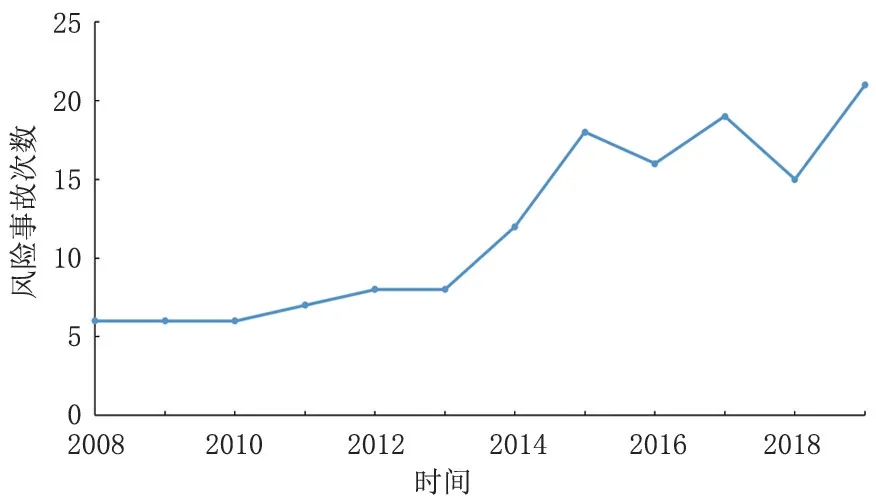
圖1 2008-2019年某液化天然氣工廠設備風險事故時序圖Fig.1 Sequence diagram of equipment risk accidents in a LNG plant from 2008 to 2019

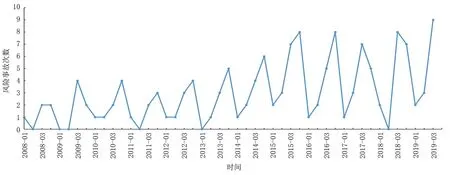
圖2 2008-2019年某液化天然氣工廠設備風險季節性時序圖（01表示第一季度，03表示第三季度）Fig.2 Seasonal sequence diagram of equipment risk in a LNG plant from 2008 to 2019（01 represents the first quarter，03 represents the third quarter）

3.2 ARIMA模型識別

殘差的自相關函數圖以及殘差的偏自相關函數圖如圖3 和圖4 所示。通過對兩圖進行分析可以發現，當殘差的滯后值達到lag=14 時，兩種函數出現了截尾性現象，同時其自相關系數不等于0，可以將參數q和Q均設定為1；當殘差的偏自相關函數滯后值lag=14 時，其偏自相關系數也不等于0，所以可以將參數p和P均設定為1。

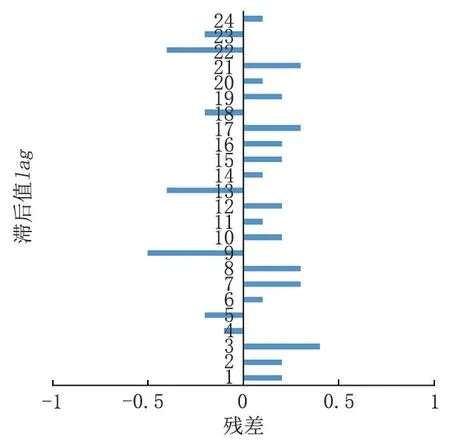
圖3 殘差的自相關函數圖Fig.3 Autocorrelation function graph of residuals

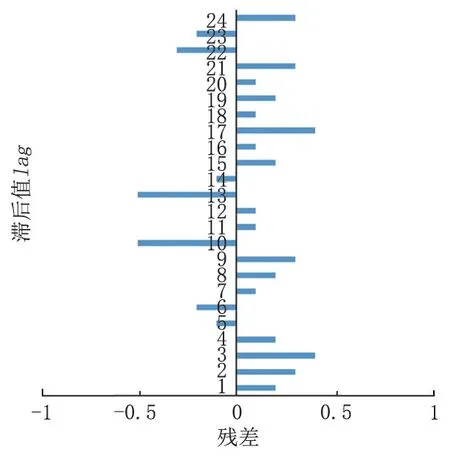
圖4 殘差的偏自相關函數圖Fig.4 Partial autocorrelation function graph of residuals

將Y1作為模型中的因變量，將表2中的影響因素作為自變量，使用matlab軟件對各個階數進行全面的計算，最終得到最佳的模型是ARIMA（1，1，1）（1，1，1）14，該模型的各種統計量見表3。

表3 最佳模型的統計量Tab.3 Statistics of the best model

通過對表3進行深入分析可以發現，殘差的自相關函數以及偏相關函數都處于可信的區間之內。其中Ljung-Box的統計量數值達到了22.84，其顯著性也達到了0.082，證明這種差異并沒有統計學上的意義，可以將原假設否定，即殘差序列存在白噪聲，序列屬于一種隨機的序列，平穩后的R2（表示相關系數）達到了0.721，正態化的BIC 值也達到了-2.37，說明模型的擬合度相對較好，可以用于數據的預測。該最佳模型的t檢驗結果見表4。通過對表4進行分析發現，該最佳模型已經通過了t檢驗。

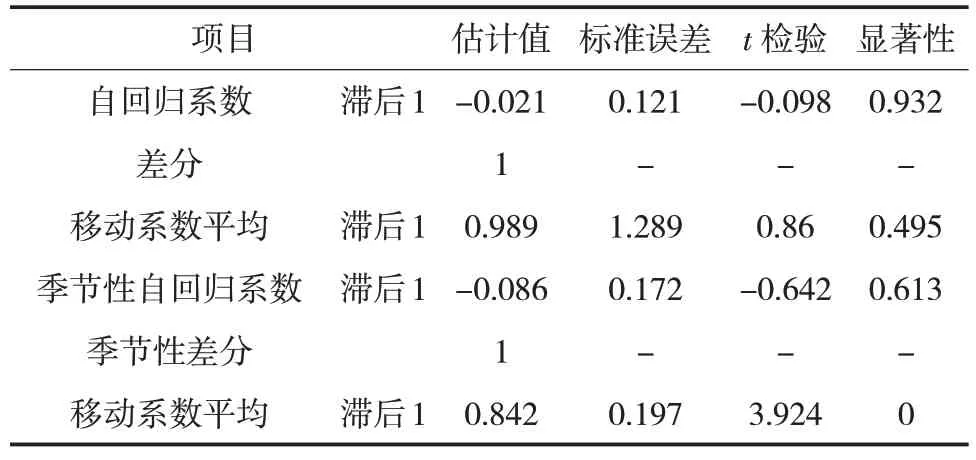
表4 最佳模型的t 檢驗結果Tab.4 t test results of the best model

3.3 LS-SVM模型識別

在使用LS-SVM模型算法的過程中，其預測的精度與核函數以及相關參數設置有關，本次研究使用的核函數為徑向基核函數，公式為

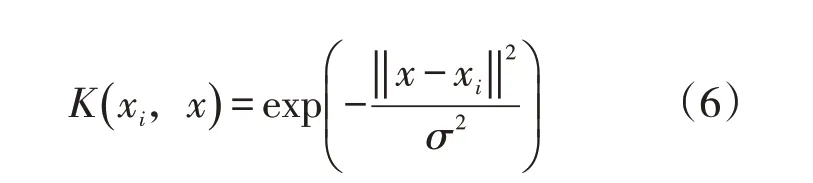
在使用徑向基核函數的前提下，可以通過多次試算的方式，確定兩種參數數值，即C=12，σ=0.001，通過設定參數使得模型的泛化能力得到了增強。為了防止出現計算飽和問題，需要對偏差進行歸一化處理，進而對2018 年和2019 年的數據進行全面的預測。

3.4 BP神經網絡模型識別

在使用BP 神經網絡模型的過程中，輸入層為年度、季度以及表2 中的7 項影響因素，在考慮樣本數量的前提下，將隱含層設定為1，輸出層為該液化天然氣工廠設備風險事故的次數，激活函數使用默認函數，錯誤函數選擇平方和方式，訓練樣本的個數為40個，測試樣本的個數為8個，該模型的統計量見表5。

表5 模型統計量信息Tab.5 Model statistics information

3.5 組合模型預測

ARIMA 模 型、LS-SVM 模 型以及BP 神經網絡模型等三種模型的預測結果與實際值之間的對比情況見表6。根據相對誤差的大小，進而可以確定各種模型的權重，權重確定情況見表7。

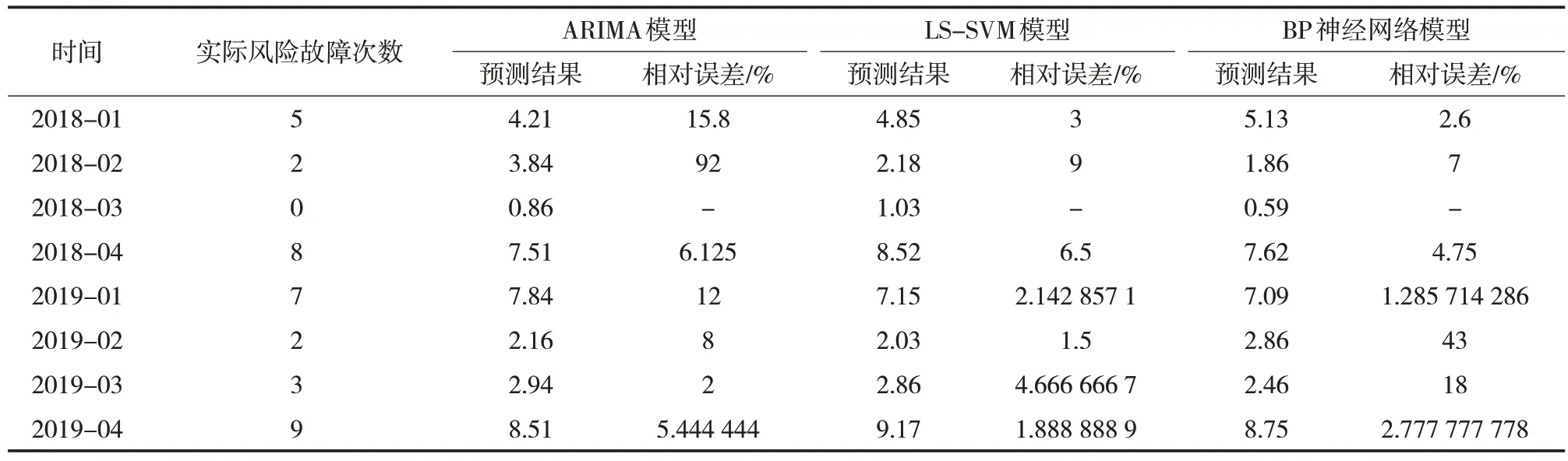
表6 三種模型預測結果Tab.6 Prediction results of the three models

通過對表7進行分析可以確定，本次研究提出的組合模型是：Y=0.241 584×Y1+0.311 784×Y2+0.446 632×Y3。使用組合模型對2008—2017 年該液化天然氣工廠設備風險事故進行擬合，擬合結果如圖5所示。

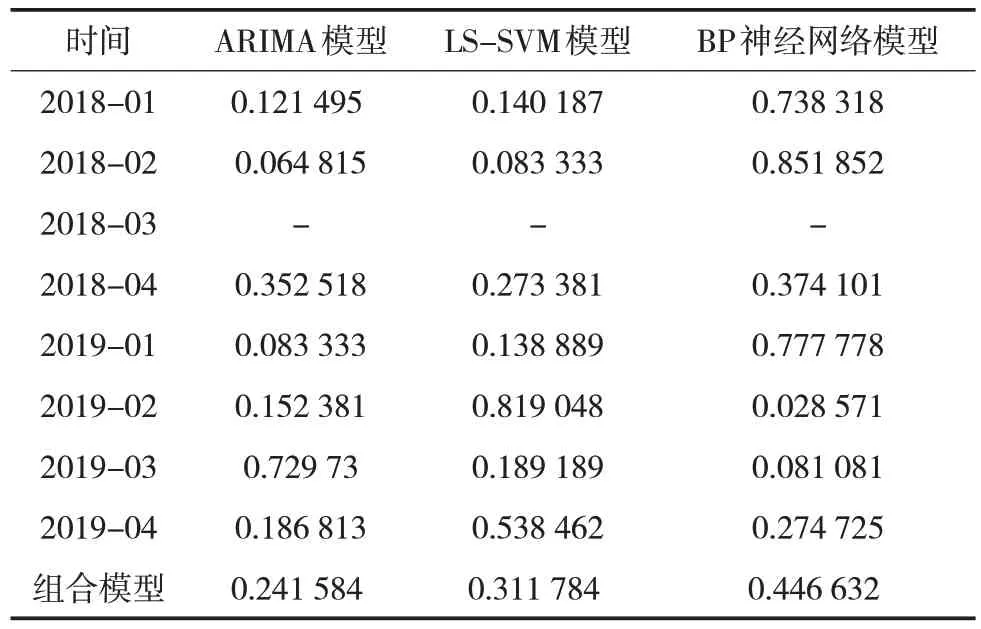
表7 權重分配情況Tab.7 Weight distribution

通過對圖5進行分析可以發現，組合模型的擬合結果與實際風險事故的發展趨勢相同，每個季度的風險事故擬合值都處于置信區間之內。組合模型的最大相對誤差為16.00%，出現在2014 年的第二季度，2008 年第二季度、2011 年第二季度以及2012 年第二季度的相對誤差也相對較大。最小相對誤差小于1%，擬合值在拐點位置處的誤差相對較大。由此可見，該組合模型可以反應出該液化天然氣工廠設備風險事故的波動情況，擬合值與實際狀況之間具有很強的重合度，證明組合模型的精度相對較高。

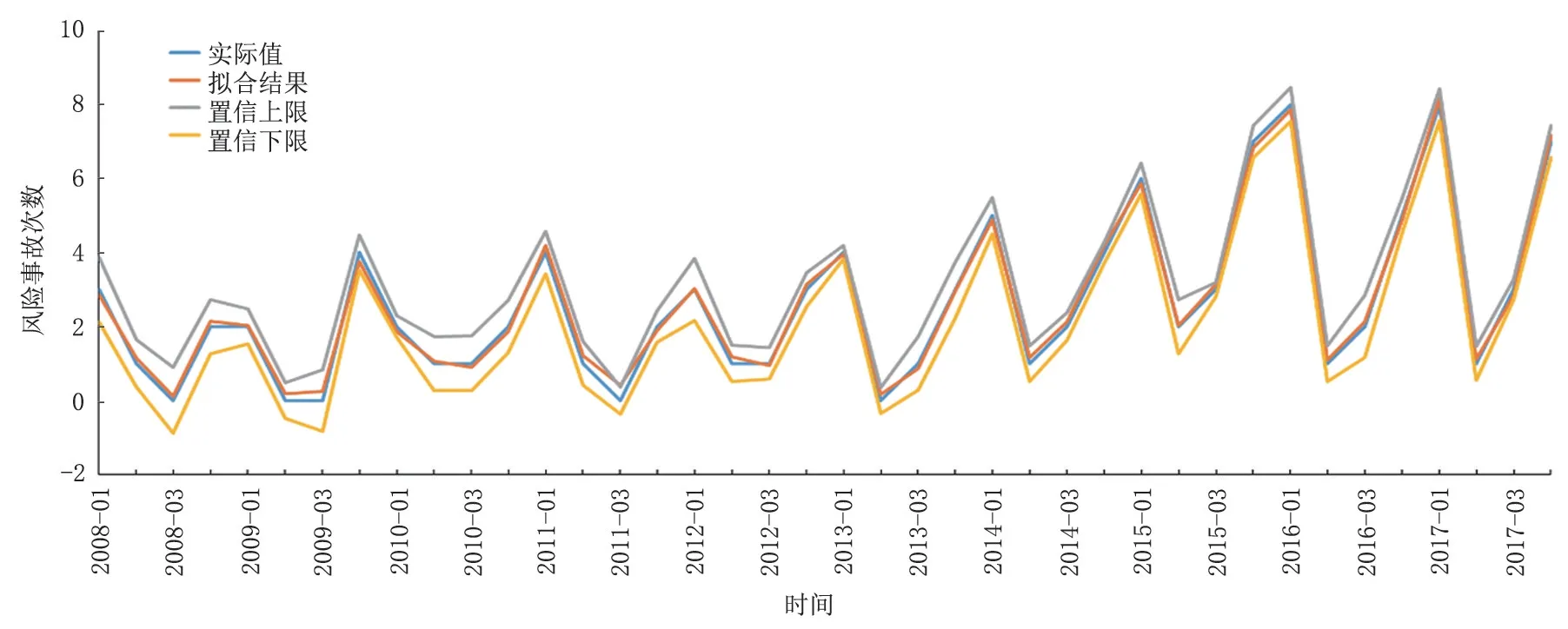
圖5 2008—2017年某液化天然氣工廠設備風險事故次數擬合結果Fig.5 Fitting results of the number of equipment risk accidents in a LNG plant from 2008 to 2017

3.6 預測結果分析

使用組合模型對該液化天然氣工廠2018 年和2019 年的設備風險事故進行預測，并與實際狀況進行比較，預測結果如圖6 所示。通過對圖6 進行分析可以發現，該液化天然氣工廠內的設備風險事故次數處于波動式上升階段，隨著時間的推移，出現風險事故的次數逐漸增加。組合模型的預測結果與實際狀況相吻合，與單一的模型相比，組合模型的精度得到了較大的提升。通過對預測結果進行全面的分析可以發現，組合模型可以反應出該液化天然氣工廠設備風險事故次數的動態變化情況，可以對液化天然氣工廠設備風險事故進行短期的預測。組合模型的精度雖然得到了提升，但是仍然存在一定的誤差，模型的精度仍然有待提升。通過研究可以證明，使用該組合模型可以對液化天然氣工廠內所有動設備以及靜設備出現風險事故的次數進行全面的預測，而出現風險事故并不意味著設備失效，但必然會對其運行效率以及運行安全產生影響。因此，液化天然氣工廠內的工作人員需要根據風險事故的發展趨勢，提前制定有效的預案，及時解決設備的運行問題，保障生產效率和生產安全。

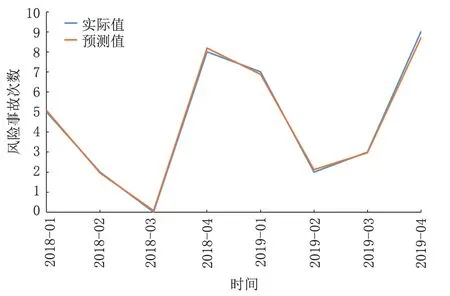
圖6 2018—2019年某液化天然氣工廠設備風險事故預測結果Fig.6 Prediction results of the equipment risk accidents in a LNG plant from 2018 to 2019

4 結論

在本次研究中，以某液化天然氣工廠2008—2019 年的設備風險事故真實數據為依據，進而建立了設備風險事故預測的組合模型，進行了模型的實例驗證。通過本次研究主要可以得出以下結論：

（1）本次研究提出的組合模型主要是根據設備風險事故歷史數據的線性以及非線性特征，對特征進行提取，然后進行參數估計以及驗證，驗證結果顯示，其預測結果可以為液化天然氣工廠企業制定設備風險事故的預防措施提供數據支撐。

（2）在使用組合模型的過程中，充分考慮了其他因素對設備風險事故次數的影響，對單一模型的誤差進行了全面的修正，結果顯示，通過使用大數據對樣本進行全面的訓練，可以使得組合模型的精度得到明顯的提升。使用組合模型可以對液化天然氣工廠內設備風險事故出現次數的發展趨勢進行預測，預測精度相對較高。但是由于液化天然氣工廠內設備風險問題較為復雜，所以在預測的過程中只能進行季度性預測。

（3）本次研究主要是通過使用歷史數據對未來狀況進行預測，但是在同一個時間點可能會出現多種類型的設備風險事故，此時就會出現離群現象，進而使得模型的預測精度降低，因此模型在使用的過程中，液化天然氣企業需要從實際情況出發，將預測周期控制在2～3年，這可以與液化天然氣工廠企業制定年度計劃相吻合，更利于液化天然氣企業制定完善的預防措施，全面防止出現設備風險問題。