基于人均延誤的交叉口信號配時優化

李 娟，賈庭勇,2

(1.西南交通大學 交通運輸與物流學院，四川 成都 611756;2. 西南交通大學 綜合交通運輸智能化國家地方聯合工程實驗室，四川 成都 611756)

0 引言

早期的交叉口信號配時方法僅以機動車為研究對象，通過建立使機動車車均延誤最小、停車次數最少或保證綠燈時期車輛全部駛出進口道為目標的模型對信號控制方案進行設計，典型的模型包括Webster配時法[1]、ARRB法[2]和HCM(2010)[3]。此類方法將所有機動車等同看待，無法體現大客車載客多的特性[4]。鑒于此，相關學者從人均延誤角度提出信號配時優化模型，引入機動車乘客數作為修正參數，消除了不同類型機動車載客率的差異性[5-7]，但上述研究均未涉及到非機動車和行人。

在信號控制交叉口，機非混合行駛常常造成交叉口通行秩序混亂，影響了交叉口的通行效率和安全[8-9]。為此，相關學者對混合交通流環境下機非運行特性及相互沖突情況進行了深入研究：蔣海峰[10]在其博士論文中詳細研究了混合交通流的干擾機理問題；景春光等[11]根據交叉口機非沖突情況，提出了非機動車提前截止時間和臨界流量計算模型[11]；但上述研究只是將非機動車和行人當作干擾因素進行考慮，未從整體上對機非混合條件下的信號控制作優化研究。陳小紅等[12]、王雪元[13]將非機動車和行人統一看作慢行交通，在混合交通條件下對交叉口進行信號配時優化研究，但前者在慢行延誤計算時未對不同轉向交通流作區分，后者雖詳細推導了不同轉向慢行交通的延誤計算方式，但其研究僅針對2次過街模式，未涉及到四相位交叉口左轉非機動車可以采取1次過街的組織模式。非機動車采用不同過街模式對交叉口會產生不同的影響，目前尚沒有明確統一規定左轉非機動車采用何種模式過街。楊曉光、陳曉明等[14-15]根據非機動車的不同過街模式，分別建立了非機動車影響下的機動車通行能力模型，分析不同交通條件下非機動車采用不同過街模式對交叉口通行效率的影響，但均未對信號配時情況進行研究；趙亞杰[16]針對非機動車在不同過街模式下分別做了信號配時優化對比分析，但其配時模型未區分不同交通方式之間載客率的差異性。

綜上，國外學者關于交叉口信號配時主要針對機動車進行研究，非機動車和行人往往只作為干擾因素對模型進行修正，對于非機動車不同過街模式以及不同交通方式的差異性考慮不足。因此，本研究將機動車、非機動車和行人作為研究對象，并以交叉口人均延誤最小為優化目標，對非機動車不同過街模式分別建模進行信號配時優化。最后，以實際交叉口數據為基礎進行測算，對比分析交叉口在不同交通條件下非機動車采用不同過街模式的綜合運行效果，為相關交叉口的交通組織與管控提供參考。

1 信號配時優化模型

1.1 優化目標

平面交叉口的通行延誤直接反映了交叉口的通行效率，同時也間接反映了交叉口的通行能力和交通擁擠狀況。研究表明，非飽和交通狀態下，信號交叉口延誤主要包括信號延誤、沖突延誤和繞行延誤[13]。其中，信號延誤是由于信號燈交替變換而產生的；沖突延誤是由于不同流向交通流相互交叉，導致部分交通流減速讓行而產生的，以左轉交通流造成的沖突最為顯著；繞行延誤主要針對左轉行人和非機動車，由于兩次直行實現左轉而增加過街距離，從而產生繞行延誤。本研究以典型四相位交叉口為研究對象，其左轉交通流有專用相位，沖突延誤可忽略不計。因此，機動車延誤主要考慮信號延誤部分，非機動車和行人延誤考慮信號延誤和繞行延誤。

1.1.1 機動車延誤

機動車通行延誤參考HCM2010中的延誤計算模型[3]，此模型適用于車道組飽和度X低于1的交叉口。HCM法在計算延誤時將交叉口進行了車道組劃分，基于車道組的延誤計算模型為：

(1)

(2)

dj=d1(PF)+d2，

(3)

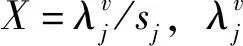
一個周期內進口道A總延誤dA及交叉口總延誤DV分別為：

(4)

(5)

1.1.2 非機動車延誤

為方便討論，在計算非機動車延誤時作如下假設：(1)非機動車到達服從均勻分布；(2)在進口道等候綠燈的非機動車，在獲得綠燈信號時，所有非機動車同時過街；(3)非機動車在每個周期內能全部放行完，無跨越周期等候的非機動車。非機動車在不同過街模式下其通行延誤不同，下面分別進行分析。

1.1.2.1 一次過街模式

四相位信號控制交叉口非機動車采用1次過街模式時，非機動車通行規則同機動車，不同流向的非機動車延誤均為1次等待綠燈的延誤。由于非機動車均勻到達，故可得相位i非機動車的平均信號延誤和一個周期內總延誤[3]分別為：

(6)

(7)

式中，C為信號周期；gi為第i相位綠燈時間；n為相位數；λbi為第i相位非機動車實際流率之和。

1.1.2.2 二次過街模式

(1)信號延誤

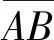
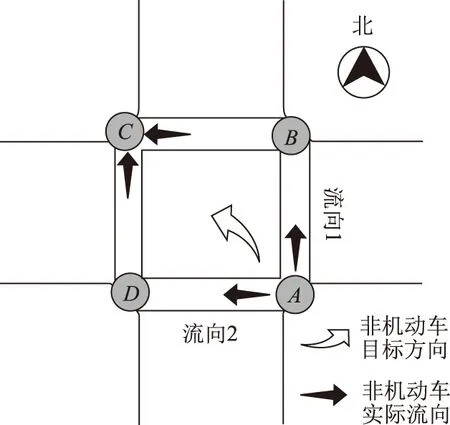
圖1 非機動車流向Fig.1 Directions of non-motor vehicle volumes

由于2次過街模式下直行非機動車和行人依然只有1次穿越街道的過程，故其延誤計算方式同1次過街模式，而不同時刻到達的左轉非機動車需要分別討論。典型四相位交叉口的信號相位方案為南北直行+南北左轉+東西直行+東西左轉，分別記為相位i=1,2,3,4。以南進口左轉非機動車為例，其選擇初始過街方向(順行方向1或逆行方向2)的概率和該方向的優先通行時間成正比，此處某方向的優先通行時間為另一方向直行綠燈結束至本方向直行綠燈結束之間的時間段，如圖2所示，g1和g2分別為兩個方向的直行綠燈時間，t2即為方向2的優先通行時間。

圖2 優先通行時間示意圖Fig.2 Schematic diagram of priority transit time

Ajj

(8)

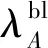
選擇順行方向的左轉非機動車中延誤最大和最小的車輛分別為第1輛車和最后1輛車，延誤值分別為：

(9)

(10)

式中，gi為該進口道直行相位綠燈時間；gi+1為其下一相位綠燈時間，當i=4時，令i+1=1；I為綠燈間隔時間；l1為順行方向街道的寬度；vb為非機動車過街速度。

根據式(9)和(10)，選擇順行方向的左轉非機動車平均信號延誤為：

(11)

同理，選擇逆行方向的左轉非機動車平均信號延誤為：

(12)

式中l2為逆行方向街道的寬度。

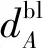
(13)

(14)

可得交叉口2次過街模式下非機動車1個周期內信號延誤為：

(15)

(2)繞行延誤

左轉非機動車2次過街模式下存在2次直行過街過程，相比于1次過街模式存在因繞行而產生的繞行延誤，假設1次過街模式下左轉非機動車的軌跡為對角線，從而左轉非機動車1個周期內交叉口總繞行延誤DBb為：

(16)

式中λbl為交叉口左轉非機動車到達率之和。

綜上，四相位交叉口非機動車總延誤可表示為：

DB=γDB1+(1-γ)(DB2+DBb)，

(17)

式中，γ取0或1，γ取1時代表非機動車采用1次過街模式，反之為2次過街模式。

1.1.3 行人通行延誤

行人在通行特性及習慣上跟非機動車有很大的相似性，在沒有行人專用道及專用相位時，一般認為左轉行人遵循2次過街規則。因此，本研究行人延誤參考非機動車2次過街模式下的計算方法，則進口道A1個周期內選擇方向j(j=1,2)的左轉行人數為：

(18)

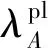
各進口道選擇順行和逆行的左轉行人平均延誤分別為：

(19)

(20)

式中vp為行人過街速度。

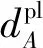
(21)

(22)

可得交叉口2次過街模式下行人1個周期內信號延誤為：

(23)

行人繞行延誤為：

(24)

式中λPl交叉口左轉行人到達率之和。

從而交叉口行人總延誤為：

DP=DPS+DPB。

(25)

1.1.4 人均延誤指標

根據不同類型車輛的平均載客率可求得整個交叉口的人總延誤，再除以1個周期內通過的總人數可得交叉口的人均延誤為：

(26)

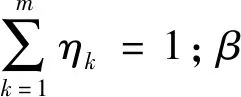
1.2 約束條件

(1)信號周期C

在一定的道路條件下，信號控制交叉口周期時長越長，一定時間內相位切換次數就越少，從而損失時間也越少，交叉口的通行能力越大，但通行延誤及排隊長度等也隨信號周期的增加而增大。因此，周期時長不宜過大，此處取最大周期時長為200 s，最短周期由最小綠燈時間等參數決定。

(2)最小綠燈時間gmin

直行相位最小綠燈時長應大于行人過街最短時間，可按式(27)計算[17]：

(27)

另外，非機動車1次過街模式下，左轉相位綠燈時間應大于非機動車過街時間，其計算式如下：

(28)

(3)飽和度α

交叉口飽和度α取值范圍設定為(0.7～0.9)。理由是：當交叉口處于欠飽和狀態(α<0.7)時，通行能力遠大于交通需求，交叉口運行通暢，進行信號配時優化的效果不明顯；當交叉口處于過飽和狀態(α>0.9)時，交叉口車流狀態極不穩定，容易造成大面積阻塞，采用信號配時優化往往不能得到理想效果。

1.3 優化模型

本研究信號配時優化模型如下：

(29)

1.4 求解算法

上述配時優化模型是在給定約束條件下計算各相位綠燈時長，從而使整個交叉口的人均延誤最小，而粒子群(Particle Swarm Optimization, PSO)算法正是一類非確定的全局最優型算法[18]，鑒于其不依賴于問題本身數學性質，且具有良好的全局搜索能力和穩健性，本研究采用PSO算法對模型進行求解。PSO算法的粒子速度和位置更新公式為：

vid(t+1)=ωvid(t)+c1r1[Pid(t)-Xid(t)]+

c2r2[Pgd-Xid(t)]，

(30)

Xid(t+1)=Xid(t)+vid(t)，

(31)

式中，vid(t)，Xid(t)分別為第t代粒子第i個變量速度和位置的第d維，其中，vmin≤vid≤vmax，vmin、vmax為粒子速度最值；Pid(t)為第t代粒子第i個變量個體極值的第d維；Pgd為全局最優解的第d維；r1，r2是屬于[0,1]的隨機數；c1，c2是加速常數，根據Huang，c1=c2=2時可以得到很好的收斂最優解。ω為慣性系數，為平衡算法的尋優能力，采用魏秀業等[20]的方法動態選擇慣性系數對PSO算法進行改進，其調整公式為：

(32)

式中，ωmax，ωmin分別為慣性系數最大值和最小值，此處分別取1.2和0.2；t為迭代次數，T為最大迭代次數。

2 案例分析

2.1 基礎數據調查

根據研究對象特點，選取成都市一環路與洗面橋街交叉口進行實例研究。該交叉口一環路方向交通量較大，洗面橋街左轉車輛較多，晚高峰時期偶爾出現擁堵現象。交叉口渠化及信號相位示意圖如圖3所示。

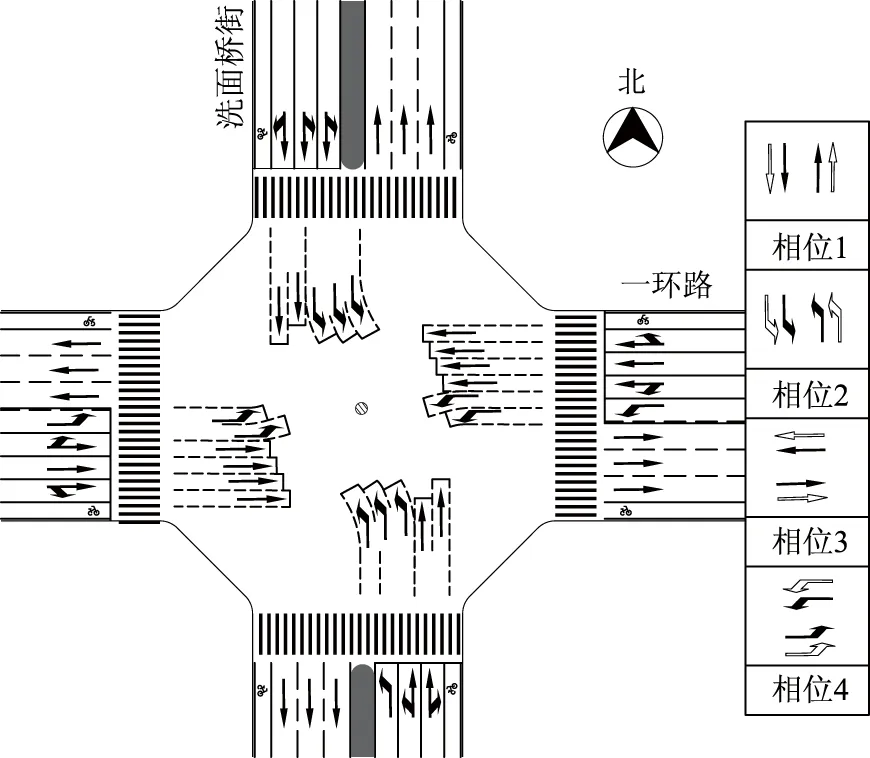
圖3 交叉口示意圖Fig.3 Schematic diagram of intersection

根據實地交通調查及相關計算得到該路口工作日(2020年8月17日，星期一)晚高峰時段(17:00—18:30)的交通量情況如表1所示。其中，機動車以小客車和大客車為主，其他類型車輛比例很小，此處暫不考慮；行人流量相對較小，且轉向比例較為均衡，文中做等比例轉向處理。經統計，該路口晚高峰時段小客車平均載客數為2.2，大客車平均載客數為13.3，非機動車平均載客數為1.1。

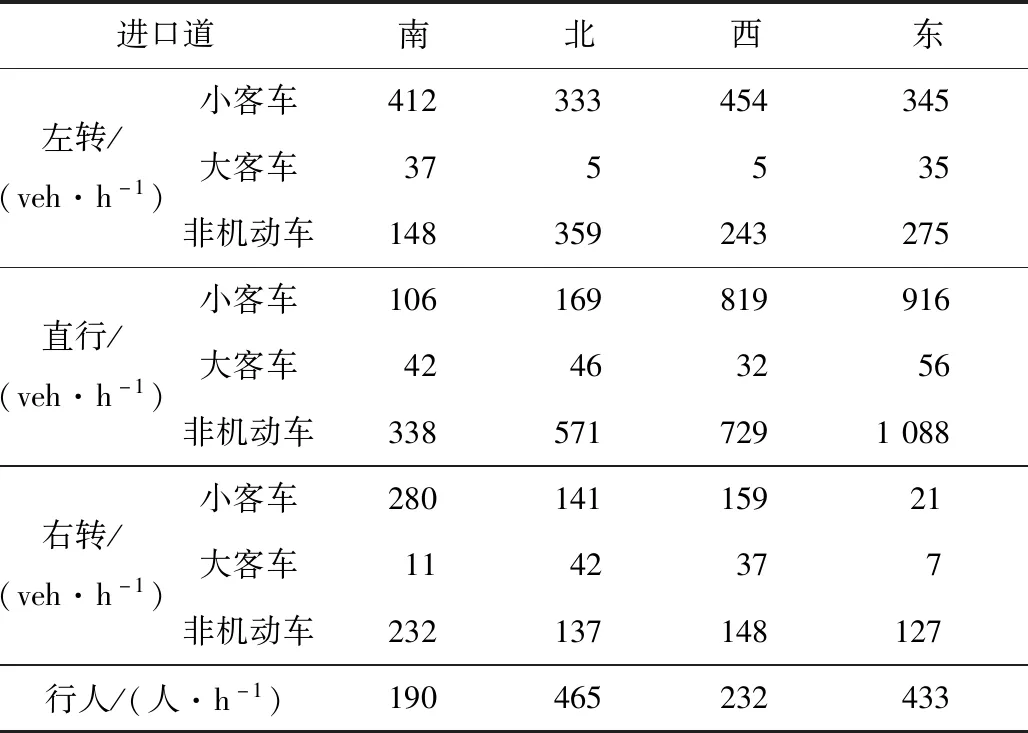
表1 交叉口晚高峰時段交通量Tab.1 Traffic volume at evening peak hours at intersection

本研究交叉口各車道組飽和流率采用交叉口的實測數據。通過現場拍攝視頻的方式記錄交叉口的通行情況，并通過電腦軟件逐幀處理，測算各車道組的飽和車頭時距。飽和流率可用下式計算：

(33)

式中h0為飽和車頭時距。

剔除異常數據后，得各進口道不同流向飽和流率見表2，各相位綠燈間隔時間均取5 s。由于該交叉口非機動車大部分采用2次過街模式，故表中左轉非機動車飽和流率參照文獻[21]確定。

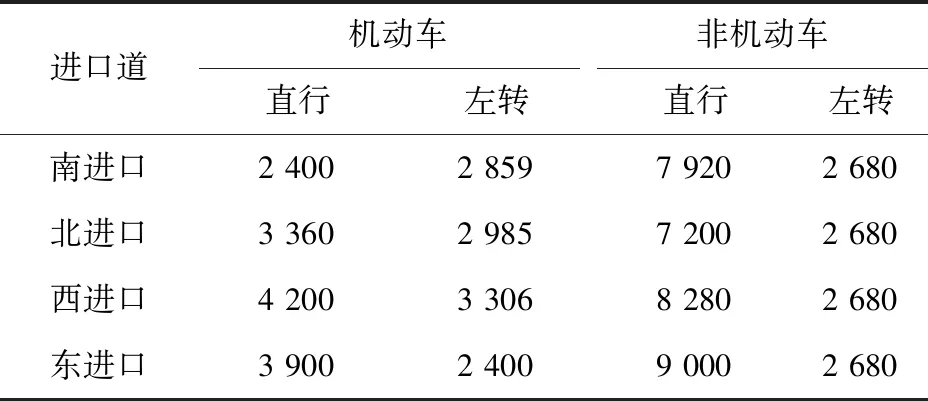
表2 各流向飽和流率 (單位：veh/h)Tab.2 Saturation flow rate in each direction (unit: veh/h)

2.2 算法求解結果

使用軟件MATLAB R2014b(8.4.0)進行編程，運用改進粒子群算法對信號配時優化模型進行求解，相關參數設置如下：最大迭代次數T設置為1 000，目標函數自變量為各相位綠燈時間，因此個數為4，粒子速度最值分別為-5和5，初始速度和位置通過隨機化產生，粒子群規模M設置為50，算法達到最大迭代次數時終止。通過MATLAB求解得優化模型配時參數與傳統webster法配時及現狀配時參數對比見表3。

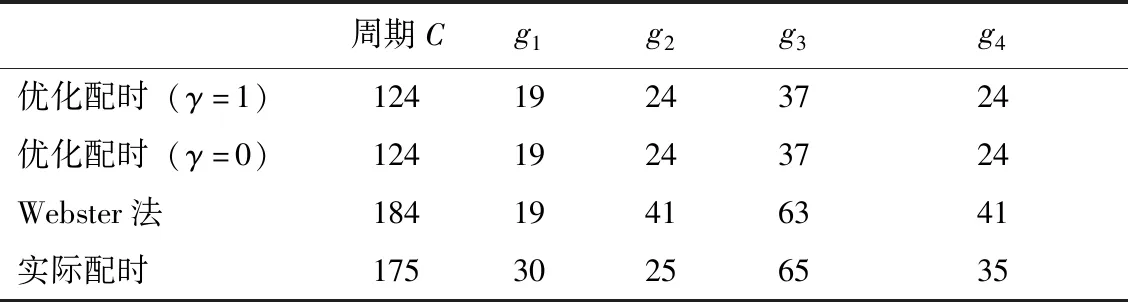
表3 優化前后信號配時 (單位：s)Tab.3 Signal timing before and after optimization (unit：s)

2.3 優化結果評價

將交叉口交通流數據及優化前后信號配時參數分別代入文中人均延誤模型，計算交叉口的人均延誤，并和Webster配時法進行對比，如表4所示。從表4中可以看出，本研究的信號配時模型的人均延誤比Webster法和實際信號配時分別降低18.3，13.5 s，優化比例分別為30%，24%。從非機動車的不同過街模式來看，現有交通條件下，1次過街模式(γ=1)比2次過街模式(γ=0)人均延誤低1.3 s，交叉口非機動車適宜設置1次過街模式。

表4 交叉口人均延誤 (單位：s)Tab.4 Delay per capita at intersection(unit: s)

2.4 靈敏度分析

為進一步研究交叉口在不同流量條件下非機動車兩種左轉模式的適用性，保持行人流量不變，通過改變機動車和非機動車左轉流量進行分析，不同左轉流量下人均延誤及相應的信號配時情況見表5。

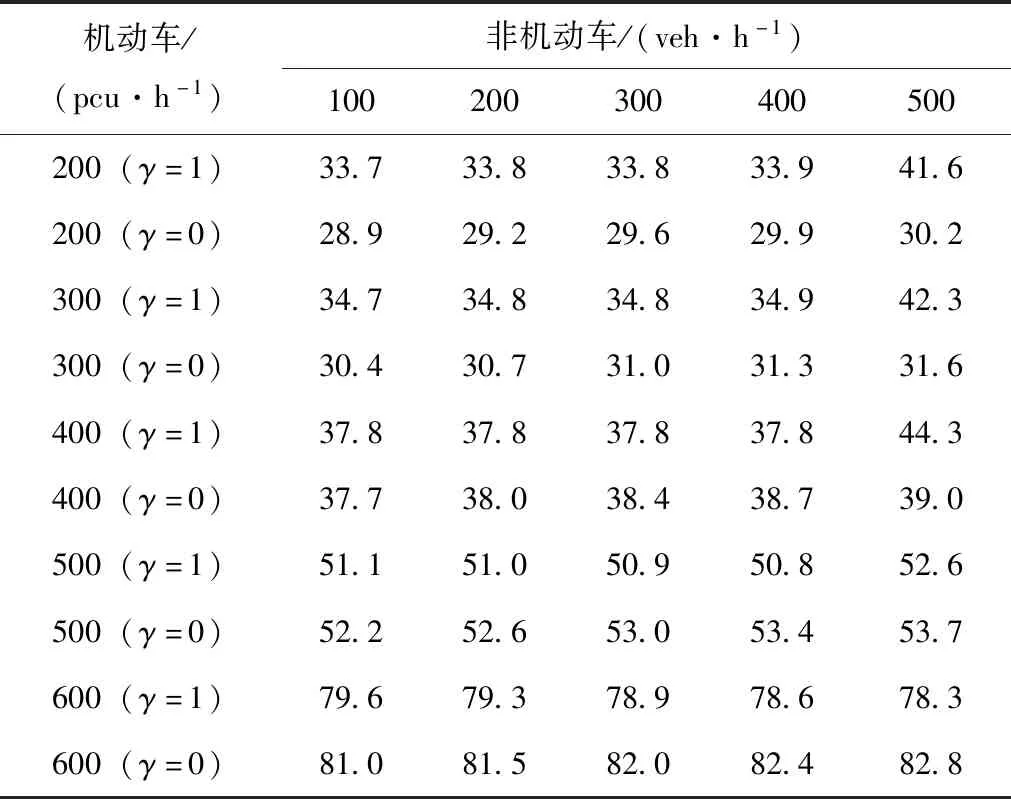
表5 不同左轉流量下人均延誤Tab.5 Delay per capita with different left-turn volumes

根據表5可得不同左轉流量下非機動車兩種過街模式的人均延誤變化情況如圖4所示。

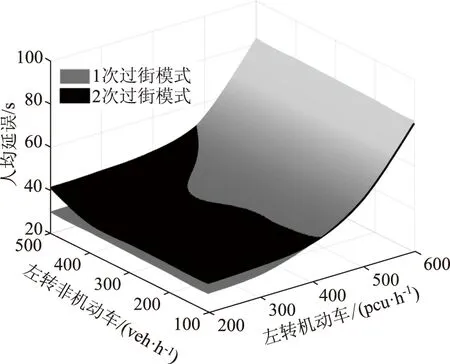
圖4 不同左轉流量下人均延誤Fig.4 Delay per capita with different left-turn volumes

由圖4可知，當左轉機動車流量大于400 pcu/h 時，1次過街模式的人均延誤低于2次過街模式，且二者延誤的差值隨左轉流量的增大而增大；當左轉機動車流量小于400 pcu/h時，1次過街模式的人均延誤大于2次過街模式，且二者的差值隨左轉流量的減小而增大。當左轉機動車流量為400 pcu/h，左轉非機動車流量大于200 veh/h 時，1次過街模式的延誤小于2次過街模式，且二者的差值隨著左轉流量的增大而增大；但當左轉非機動車流量增大到500輛/h時，1次過街模式的延誤急劇增加，此時2次過街模式的延誤更小。

結合前文分析，造成上述現象的原因是：當機動車左轉流量大于400 pcu/h時，由于左轉非機動車1次過街模式只有1次過街過程，其信號延誤和繞行延誤都比2次過街模式小。而當機動車左轉流量小于400 pcu/h時，2次過街模式下交叉口可根據左轉流量對左轉綠燈時間進行同步調整，而1次過街模式由于左轉非機動車最短過街時間限制，無法進一步減小綠燈時間，由此造成交叉口人均延誤高于2次過街模式。另外，當左轉機動車流量為400 pcu/h，左轉非機動車流量增加到500 veh/h時，由于左轉相位非機動車的飽和度約束，導致左轉綠燈時間和信號周期變長，從而交叉口人均延誤顯著增加。

結合不同左轉流量下的信號配時情況可進一步求得各關鍵相位飽和度。可以發現，當機動車左轉流量較小時，南北向直行相位的飽和度偏低，綠燈時間未充分利用，如表6所示。

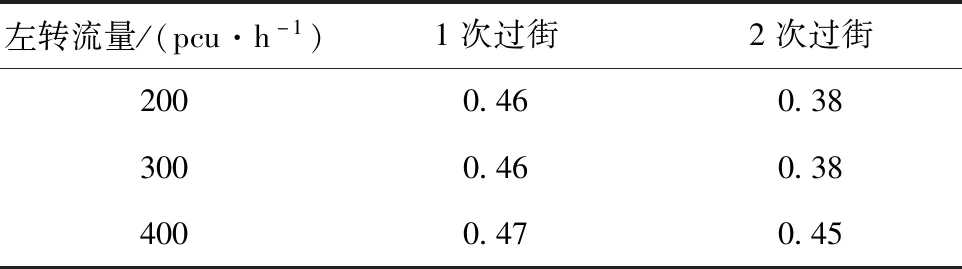
表6 南北向直行關鍵相位飽和度Tab.6 Saturation rates of key phases in north-south straight direction

結合交叉口幾何參數分析，造成此現象的原因是，南北向直行行人過街距離較長，直行相位最短過街時間限制了信號配時的進一步優化。

3 結論

本研究提出的基于人均延誤的交叉口信號配時優化模型，綜合考慮了交叉口所有交通參與者的通行效益；同時，以人均延誤為優化指標消除了不同交通方式之間載客率的差異性。通過對交叉口非機動車不同過街模式分別建模優化，對比分析交叉口在不同交通條件下采用兩種模式的運行效果，為同類型交叉口的交通組織與管控提供了依據。文中對2次過街模式下的非機動車和行人延誤計算方法進行了修正，其科學性還需在實際應用中進行驗證。

另外，筆者研究發現，交叉口非機動車和行人過街的最短綠燈時間對交叉口的信號配時優化效果有很大影響。1次過街模式下，根據式(27)，左轉非機動車過街時間與兩條街道的寬度有關，未來可在本研究基礎上進一步研究非機動車過街模式適用性和街道寬度之間的關系。根據式(26)，行人最短綠時間和街道寬度直接相關，可通過增設交通島，或利用中央駐足區設置行人多步穿越街道的組織方式，并配置相應信號燈，以此來縮短行人過街距離，減少行人過街時間。如南北向部分直行行人可利用東西向左轉相位提前穿越一半街道到中央駐足區等待，并在南北向直行綠燈亮起時穿越后半段街道實現過街。