一種管道探測蛇形機器人的建模仿真與實驗研究

鄧 蕊，王亞慧，邢利輝，侯坤昊

(北京建筑大學 電氣與信息工程學院，北京 100044) E-mail：18833633026@163.com

1 引 言

管道運輸憑借方便快捷、運輸量大、成本低等優點，在燃氣輸配等領域有著至關重要的作用.然而大量的管道在投入運營后，長期受到運輸介質、外部環境的腐蝕以及外力的沖擊等影響，很可能出現管道裂紋、泄露、截留面積減小等.所以就需要定期對管道進行檢查、維護和清潔保養[1].由于管道多是深埋地下且大多輸送介質是對人體有害的，使得工作人員無法直接對管道進行檢測和維修.

基于此，業內的研究人員提出了利用機器人替代人對管道進行日常維護和檢測的新思路[2，3].經過近些年的研究發展，目前用于管道探測的機器人主要有輪式[4]和履帶式機器人[5].但這兩類機器人僅適應于大直徑水平管道的檢測，對于小直徑以及垂直管道卻無能為力了.針對此背景，我們提出并研制了一種用于管道內部檢測的蛇形機器人，適用于200～500mm的管徑.該蛇形機器人在管道中以行波或螺旋的多步態方式運動，能適應各種管道不同的管徑要求，利用其在管道內靈活運動的特點進行管道檢測，對可能出現的安全隱患進行排查.

2 蛇形機器人機械結構的設計

由于管道具有不同的管徑和材料特性，且內部空間狹小、復雜，所以蛇形機器人需具備輕量、小型、靈活運動等特性[6].其樣機采取關節模塊化的設計，根據不同直徑的管道靈活地增減模塊數量來實現重組[7，8]；關節之間使用輕質鋁合金部件進行連接，選用RDS3115大扭矩舵機來保證運動時有足夠的動力；考慮蛇形機器人與管道間為軟接觸，設計了韌性較強、摩擦力較大的圓柱形橡膠外殼；為具有穩定的能源供給，采用拖纜的形式供電；為使機器人有效完成管道多步態運動和檢測作業，采用正交連接的方式串聯成蛇形機器人的樣機.蛇形機器人要創建空間中的三維運動[9]，需要具備3個前提條件：1)每個模塊的舵機必須提供足夠的扭矩來維持其角度輸出[10]，采用大扭矩的舵機來滿足動力需求;2)關節間的鋁制連接件必須具有足夠的結構完整性，可保證其承受力和剛性強度足以抵制蛇形機器人運動時而產生的力;3)蛇形機器人依靠外殼與管道摩擦向前運動，于是外殼要有摩擦系數大、軟接觸和耐腐蝕特征，我們采用橡膠作為外殼材料.

2.1 模塊的結構化設計

根據生物蛇的骨骼結構和運動機理，管道探測蛇形機器人可由多個重復模塊來搭建[11].每個關節由一個舵機、兩個不同尺寸的U型連接件、舵盤等部件組成.搭建蛇形機器人框架時，后一個關節在前一個關節的基礎上，依次旋轉90°連接.單個模塊由舵機、U型承重件、控制器、外殼以及傳感器等組成.舵機模塊見圖1.

圖1 舵機模塊的實物圖Fig.1 Physical picture of steering gear module

蛇形機器人的動力源由每個模塊中的雙軸數字舵機提供，通過舵機的輸出軸連接U型主支架提供運動時的扭力，利用舵機的另一端連接U型副支架使整個關節受力平衡.舵機由MCU的定時器輸出的PWM波驅動，通過設定PWM波的不同脈沖寬度來控制舵機的旋轉角度.利用內部的電位計閉環位置反饋電路，形成了能抵抗外部環境的強位置鎖定功能.RDS3115舵機可在-90°-90°(擺臂和舵機平行默認0°)之間變化，其相應的參數見表1.

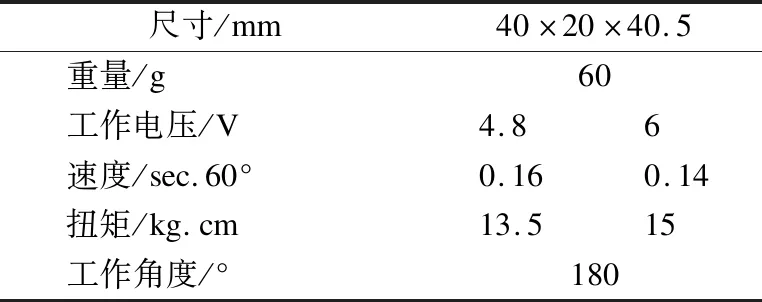
表1 舵機RDS3115的規格參數Table 1 Specifications of steering gear RDS3115

2.2 外殼設計

蛇形機器人的外殼設計是整個設計中關鍵一環，它不僅影響外殼與管壁的接觸效果，還會影響蛇形機器人的運行速度.在運動的過程中，蛇的周身都可能與管道內壁進行接觸，結合模塊內部的舵機、控制器、U型連接件等部件的尺寸，將外殼設計成圓柱形外殼，并采用摩擦系數較高的(泊松比為0.324，楊氏模量為7.8×105psi)橡膠材質，這樣就大大提高了蛇形機器人的運動效率和安全性.圖2為外殼的整體樣貌，目的是方便將舵機等部件裝入殼中，進行裝配.通過半個外殼兩邊的螺絲孔，加以固定.

圖2 外殼的整體樣貌Fig.2 Overall appearance of the shell

3 蛇形機器人建模與仿真

3.1 基于MATLAB的運動學建模與仿真

正交連接蛇形機器人是一種自由度較高、控制比較復雜的串聯機器人.因在關節旋轉角的最大容許范圍內，關節的粗細不影響整個蛇形機器人的運動，所以這里將其抽象為空間連桿機構以簡化模型的建立.而D-H分析法[12]是機器人運動學分析最常用的方法之一，利用坐標變換，能夠把蛇形機器人的相對位姿準確地描述出來.

因蛇形機器人是移動機器人，無固定的底座，所以建立D-H坐標系時，基座標O0可任意，現以6關節為例.首先在每一個關節上建立一個局部坐標系，相鄰關節之間采用4×4的變換矩陣來表述空間關系；然后依次通過矩陣相乘，求出每一個關節相對于基座標的位姿，直至末端.最后由此建立蛇形機器人的運動學方程.

其他關節的坐標系原點O位于旋轉副軸線的中點，Z軸位于旋轉副的軸線上，方向從被動擺臂指向主動擺臂，X軸方向指向下一個關節，位于蛇體的中心軸線上.另外，Y軸的方向由右手定則來決定.生成的D-H標準坐標系如圖3所示，其它關節的坐標系之間存在3個約束關系(尾部基坐標系除外)：1)相連兩個坐標系的Z軸相互垂直，逆時針依次旋轉90°；2)下一個關節坐標系的原點在上一個坐標系X軸的輸出軸線上；3)相隔兩個坐標系的Z軸方向相反.我們假設坐標系O1和基座標的方向相同，根據圖3建立的坐標系，生成蛇形機器人各關節之間的平移、旋轉參數，其中θi為xi-1繞zi-1到xi軸的轉角；di為xi-1沿著zi-1到xi軸的距離；Ai為zi-1沿著xi到zi軸的距離；δi為zi-1繞xi到zi軸的轉角.具體如表2所示.

圖3 蛇形機器人的D-H坐標系示意圖 Fig.3 D-H coordinate system of snake-like robot

表2 蛇形機器人D-H參數表Table 2 D-H parameter table of snake robot

i=1，2，…，n

(1)

將表2中的具體參數代入式(1)，得：

(2)

根據上述的D-H參數表和轉換矩陣的齊次變換，可求出蛇形機器人的運動學模型：

(3)

仿真驗證：

利用MATLAB[13]，以32個關節為例，每個關節7cm，按照上述D-H分析法的建模思想，編寫程序，根據相鄰關節間的坐標變換矩陣，依次經過齊次變換求得末端關節相對于基座標的位姿，即建立起蛇形機器人的運動學模型.通過運動控制函數控制蛇形機器人運動學模型中的各關節運動，使各關節舵機轉動相應的角度，獲得蛇形機器人運動學正解；與系統機器人工具箱自帶的正解函數比對，驗證模型正確.圖4為運動學正解的對比結果，即蛇形機器人尾部關節相對于基座標的總變換矩陣，4×4的齊次變換矩陣的最后一列為尾部關節相對于基座標的空間位姿(Px，Py，Pz).

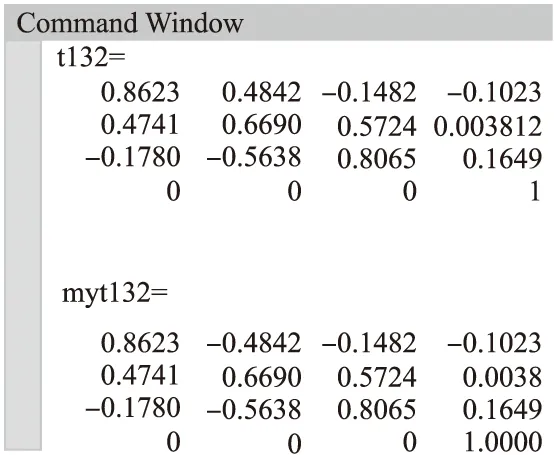
圖4 運動學正解的結果比對Fig.4 Comparison of results of positive kinematics

通過多次更改運動控制函數中的參數，來獲取大量不同直徑管道中蛇形機器人螺旋運動的步態數據樣本，通過粒子群算法得到控制參數與管道直徑間的關系，可求出適應一定管徑的優化運動控制參數.當管徑300mm時(以300mm為例)，運動控制函數為θi=0.9sin(πt+1.6i)，i=1，2，3…n.將此運動函數應用到模型上，根據變換矩陣的齊次運算求出各關節相對于基座標的運動學正解，根據正解中的坐標信息繪出正交連接蛇形機器人在300mm管徑內螺旋翻滾運動的空間位姿，如圖5所示.

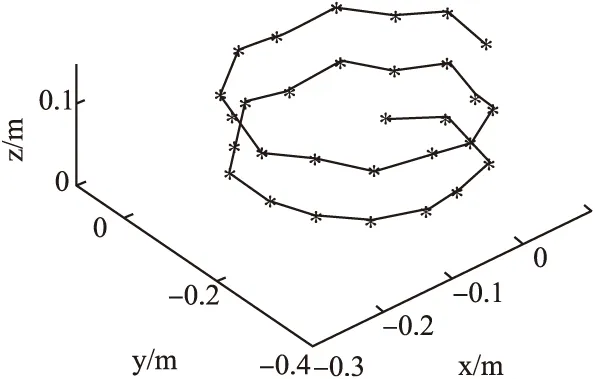
圖5 300mm管徑內t=1s時螺旋翻滾運動的空間位姿 Fig.5 Spatial position of spiral tumbling motion in 300mm pipe diameter with t=1s

3.2 基于ADAMS的動力學建模與步態仿真

機器人的動力學研究的是機器人力與運動之間的關系，其中最重要的是建立模型簡化后多連桿機構的動力學方程.蛇形機器人的樣機利用一連串的重復模塊，采用正交的特殊方式連接.我們采用牛頓—歐拉的方法[14]，通過力與力矩間的平衡關系來建模.首先，建立全局坐標系下的運動平衡方程：

(4)

其中，i=1，2……n為蛇形機器人的n個關節；Fx，i、Fy，i、Fz，i是第i個關節分別在x、y、z軸上的摩擦力分力；Hx，i、Hy，i、Hz，i，Hx，i-1、Hy，i-1、Hz，i-1為第i個關節分別與第i+1個關節，第i-1個關節在x、y、z軸上的約束力.為了方便后續的計算，上述公式用矩陣表示為：

(5)

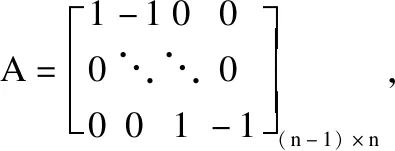
(6)

其中將各個角度的三角函數用向量和矩陣的形式來表示：cosφ=[cosφ1，cosφ2，…，cosφn]T?Rn，Cφ=diag(cosφ)?Rn×n，sinφ，sinμ，cosμ，Cμ，Sμ，Sφ同理.

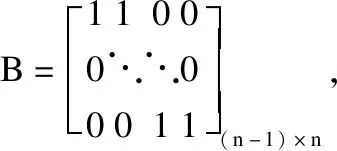
(7)

對X，Y，Z求兩階導數得：

(8)

在局部坐標系下，蛇形機器人第i個關節的受力分析見圖6.

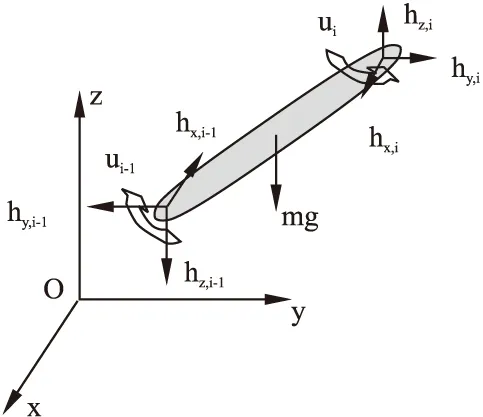
圖6 三維空間連桿的受力分析Fig.6 Force analysis of three dimensional spatial connecting rod

其中ui，ui-1為第i個關節分別與第i+1，i-1個關節的舵機力矩.設逆時針方向為正，可得到下列的力矩平衡方程：

(9)

其矩陣形式為：

(10)

將hx，hy，hz代入式(10)中，令V=BT(AAT)-1B，P=BT(AAT)-1A，整理得動力學方程為：

(11)

仿真驗證：

為了驗證動力學模型的有效性，首先運用SolidWorks三維繪圖軟件建立蛇形機器人的實際模型，然后以Parasolid格式導入到ADAMS力學分析軟件[15]，進行動力學的步態仿真.建模時，我們直接將蛇的框架和外殼裝配在一起，進行繪圖.以蛇形機器人在管道內的行波運動為例進行仿真分析，如圖7所示.

圖7 ADAMS中蛇形機器人管內行波運動Fig.7 Traveling wave motion of snake-shaped robot in ADAMS

1)根據蛇形機器人樣機的實際尺寸，在SolidWorks中建立精確的幾何模型以及管道、地面等實驗環境；

2)根據D-H的標準分析法，在ADAMS中對蛇形機器人的14個模塊建立相應的轉動副和固定副約束，并給每個轉動副添加運動約束函數.

3)按照實際設置每個模塊和管道的質量、材質、剛度、透明度等參數，最大限度地還原實際情況，并在管道與每個模塊間建立接觸力約束，設置相關的摩擦系數等.

利用GSTIFF積分求解器對蛇形機器人的管內運動進行動力學仿真，當End Time=5s，Steps=800時，正交關節蛇形機器人可以在300mm管道中平穩地做行波運動，并可通過數據后處理來分析各關節速度、角速度、扭矩等情況，同時也為度、加速度的曲線,如圖8所示.

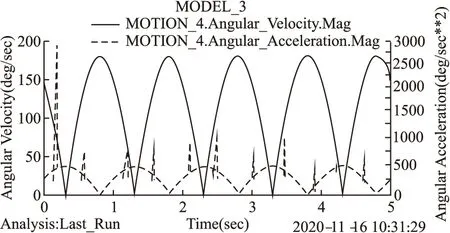
圖8 關節4的速度、加速度曲線Fig.8 Velocity and acceleration curves of joint 4

4 蛇形機器人的運動實驗

我們設計的蛇形機器人相鄰關節間采取正交的結構，即一個偏移舵機接一個俯仰舵機，依次連接而成.樣機共有14個單元模塊，每個關節加裝橡膠外殼后長65mm，寬56mm，重量為70g.利用蛇形機器人的樣機搭建實驗平臺，測試其機械結構與控制策略是否合理、可靠，舵機運動函數是否有效.

用硬質、透明的有機玻璃管模擬實際管道展開室內運動實驗(以行波方式為例)，通過控制函數計算各關節舵機的轉角，并以此來控制舵機運動方式，即：

θi=Asin(wt+pi)+εi，i=2，4，6，…，n

(12)

式中，i表示舵機的序號；θi為第i個舵機的轉動角度，A為舵機的最大容許轉角，w為舵機運動的角頻率，ρ為運動模式的控制參數，εi為角度補償.

根據3.2小結動態仿真的運動控制函數，取A=1.6，w=π，ρ=0.3，εi=0時，蛇形機器人的樣機可在300mm管徑內平穩地實現行波運動，如圖9(a)所示.根據實際刻度尺的測量，行波運動曲線的峰值為10.95cm，在10s內向前運動57cm，平均速度為5.7cm/s；另取A=1，w=π，ρ=0.3，εi=0時，蛇形機器人的運動如圖9(b)所示，根據測量，行波運動曲線的峰值為7.3cm，在10s內向前運動53cm，平均速度為5.3cm/s；再取A=1.6，w=π，ρ=0.8，εi=0時，蛇形機器人的運動如圖9(c)所示，根據測量，行波運動曲線的峰值為12.4cm，在6秒內向前運動了28cm，平均速度為4.7cm/s.

通過上述實驗觀察，蛇形機器人在運動中未出現側滑，行波運動的波形由參數A和ρ共同來決定.對比圖9(a)、圖9(b)兩組實驗，在角頻率w和ρ相同的情況下，A的值越大，蛇形機器人運動曲線的峰值越高，向前運動的速度相對越快.

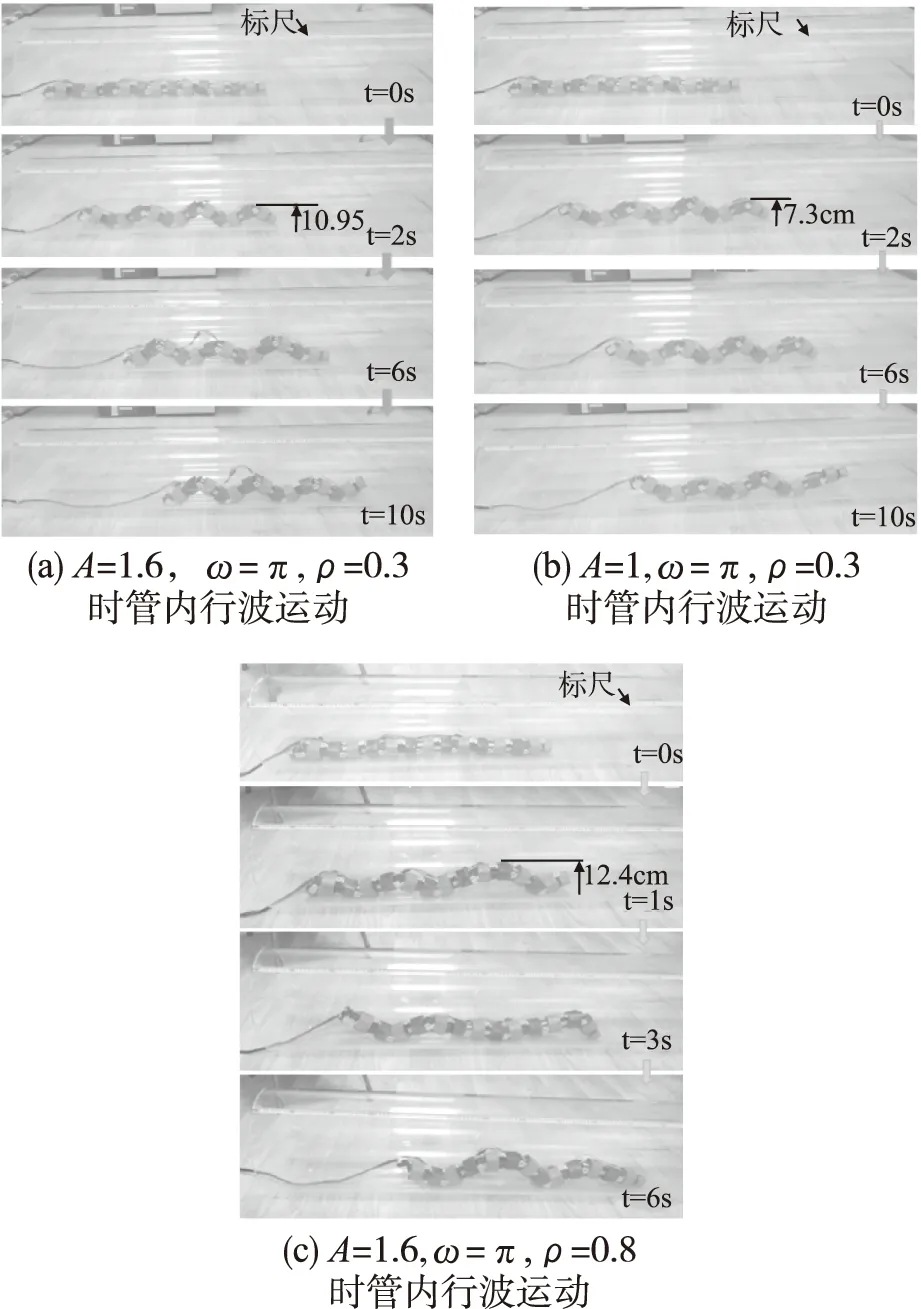
圖9 管內行波運動(以300mm管徑為例)Fig.9 Traveling wave motion inside the tube(take the pipe diameter of 300 mm as an example)

對比圖9(a)、圖9(c)兩組實驗，在角頻率w和A一定的情況下，ρ的值越大，波峰數越少，峰值越高.為方便觀察實驗結果，采用了內部光滑的透明玻璃管道，現實中的管道存在一定的摩擦，蛇形機器人運動的速度會更快.通過大量的實驗數據，在保證頭部攝像機能獲取清晰管內圖像的前提下，以最快的運行速度來選取運動控制函數中的最優參數.

5 結 論

本文基于管道探測的特點，開發了一種靈活的多步態蛇形機器人，以期應用于200～500mm內徑的傳輸氣體的管道檢測，補齊某些特殊場合下人工或其它非直接探測方法所不能解決問題的短板.具有較大的研究意義和實際的工程應用價值.本文通過研究生物蛇的骨骼結構和運動機理，結合應用環境，以及可重組的模塊化思想構建了串聯結構的蛇形機器人.獲得了以下成果：

1)首先對蛇形機器人的機械結構和外殼進行了設計；

2)利用運動學和動力學仿真平臺分別進行建模仿真，得出最優的控制參數，為現實的實驗做參考意見；

3)最后通過樣機實驗來驗證蛇形機器人管內運動的可行性、穩定性及運動能力.

縱觀目前社會發展，機器人行業發展迅猛，仿生蛇形機器人有其獨特的優點，在未來的管線探測、災難救援、軍事探險等方面有著特殊的應用價值和經濟效益.