基于遺傳算法的馬斯京根模型在巴基斯坦吉拉姆河流域應用研究

劉啟松 劉天勇 鄧頌霖

摘要：馬斯京根法作為河道洪水預報的重要方法，參數和系數的率定是關鍵和難點，直接影響預報精度。在詳細闡述遺傳算法基本思想和性能分析的基礎上，以模擬結果與實測值的誤差最小為進化目標，直接搜索馬斯京根法方程系數，獲得河道上下游流量關系方程。對巴基斯坦吉拉姆河流域查特卡拉斯至卡洛特水電站壩址段的洪水過程進行了研究，遺傳算法的平均絕對誤差為60.2 m3/s，平均相對誤差為4.87%，納什系數為0.77。結果表明：遺傳算法對馬斯京根模型參數優選問題的求解行之有效，吉拉姆河流域查特卡拉斯至卡洛特水電站壩址段洪水模擬精度較好。研究成果可為卡洛特水電站洪水預報提供技術支撐。

關鍵詞：洪水預報;遺傳算法;馬斯京根模型;吉拉姆河流域;卡洛特水電站;巴基斯坦

中圖法分類號：P338文獻標志碼：ADOI：10.15974/j.cnki.slsdkb.2021.11.004

文章編號：1006 - 0081（2021）11 - 0016 - 05

0 引 言

馬斯京根模型的基本原理是用槽蓄方程代替動量方程，用水量平衡方程代替連續方程，可利用上游斷面流量和馬斯京根模型演算下游斷面流量，流量演算精度取決于馬斯京根模型參數的精準性[1-2]。求解馬斯京根模型參數的傳統方法有試錯法和最小二乘法。傳統方法求解馬斯京根模型參數盲目性大、準確性低，需多次人工試算且不可避免會引入人為誤差。為了提高馬斯京根模型參數的估計精度，近年來國內外學者利用優化算法對模型參數進行了估計，如：遺傳算法、模擬退火算法、差分算法等[3-4]。金羽和左廣巍等[5-6]利用遺傳算法對馬斯京根模型參數進行了求解，結果表明，遺傳算法具有能較好地處理約束、跳出局部最優等優點。本文利用遺傳算法對其參數進行求解，以演算出流量過程與實測出流量過程擬合程度為優化準則，對巴基斯坦吉拉姆（ Jhelum）河流域查特卡拉斯至卡洛特水電站壩址河段進行流量演算。

1 研究區域概況

巴基斯坦卡洛特水電站位于巴基斯坦吉拉姆河流域[7-8]，壩址以上流域面積為26 700 km2，其中13 500 km2處于印控克什米爾地區，控制站為恰科迪（Chakothi）站。卡洛特水電站是巴基斯坦境內吉拉姆河規劃的5個梯級電站的第4級，上一級為阿扎德帕坦（Azad Pattan），下一級為曼格拉（Mangla）。壩址處多年平均流量819 m3/s，多年平均年徑流量258.3億m3。工程任務為發電，電站裝機容量72萬kW（4×180 MW）。巴基斯坦吉拉姆河流域（巴控區域）共有32個水文站點[9-10]，站網分布見圖1。

2 方法介紹

2.1 馬斯京根法

馬斯京根法的基本原理是用槽蓄方程代替動量方程[11-12]，用水量平衡代替連續方程：

[dWdt=I-Q]? ? ? ? ? ? ? ? ?（1）

[W=kQ=k[xI+（1-x）Q]]? ? ?（2）

式中：W為蓄水量;I為河段上斷面入流量;t為時間;Q為河段下斷面出流量;Q'為示儲流量;[x]為流量比重因子;[k]為槽蓄系數。研究表明，[k]值等于在蓄水量[W]下穩定流狀態的河段洪水傳播時間t;[x]反映水面曲線的形狀和河段調蓄作用的大小。

當已知河段上斷面流量過程時，下斷面流量可得：

[Qi+1=C0Ii+1+C1Ii+C2Qi]? ? ? ? ?（3）

其中：

[C0=-kx+0.5Δtk-kx+0.5Δt]? ? ? ? ? ?（4）

[C1=kx+0.5Δtk-kx+0.5Δt]? ? ? ? ? ?（5）

[C2=k-kx-0.5Δtk-kx+0.5Δt]? ? ? ? ? ?（6）

且：

[C0+C1+C2=1]? ? ? ? ? ? ?（7）

式中：Qi，Qi+1為時段始、末的河段下游斷面出流量;Ii，Ii+1為時段始、末的河段上游斷面出流量;C0，C1和C2為洪水演算系數;[Δt]為計算時段長。

從上式可以看出，如果求出C0，C1和C2這3個參數，就可由河道上斷面流量演算到河段下斷面流量。因此，馬斯京根算法的關鍵在于演算參數C0，C1和C2或[k]，[x]的率定[13]。

2.2 遺傳算法

遺傳算法是用數學方法模擬生物進化過程[14-15]，將“優勝劣汰，適者生存”的生物進化原理和繁殖、雜交、變異等概念引入到算法中。在遺傳算法中，將一串數據或數組作為“染色體”，按照選擇的適應度函數并通過繁殖、交叉和變異等操作對個體進行篩選。適應度高的個體將會組成新的群體，新的群體在繼承上一代群體信息的同時也優于上一代群體。這些群體不斷的重復繁殖、雜交和變異等操作，使群體中的適應度不斷提高，直至滿足一定的條件為止[16]。步驟如下：

（1）生成初始種群。利用二進制編碼等對決策變量進行編碼。隨機產生初始種群，但初始產生的種群結果一般不是最優，所以需要進行繁殖，交叉和變異等工作，目的是得到最優的個體或種群。

（2）選擇運算。在生成的初始種群中，將適應性強的個體留下，淘汰劣質個體，這樣適應性強的個體可以遺傳到下一代。

（3）交叉和變異。交叉和變異步驟是遺傳算法的核心，交叉可以將種群中的個體隨機進行交換，產生新的種群，可能會將優勝個體相互結合在一起。而變異是對種群中個體的基本進行改動，產生新的個體。交叉和變異操作能夠使遺傳算法搜索最優解能力加強[17]。

（4）進化迭代及算法終止。根據交叉和變異操作可得到新的種群，不斷重復以上操作可生成新的群體，根據求解目標，對新一代群體不斷進行評估，直至最優種群出現，算法終止[18]。遺傳算法流程見圖2。

3 實例應用

3.1 模型構建

根據對研究區域水文概況的分析，選取的研究河段為吉拉姆河流域查特卡拉斯河段至卡洛特水電站壩址河段（圖3），利用馬斯京根洪水演算模型并以河道下斷面實測值與計算值的誤差平方和為目標函數，直接優化決策變量C0，C1和C2，得到與實測流量相差最小的最佳擬合曲線，建立以下優化準則：

（1）馬斯京根模型：

[Qi+1=C0Ii+1+C1Ii+C2Qi]? ? ? ? （8）

（2）優化準則：

[min? f=i=1n-1（Qi+1-Q實，i+1）2]? ? ? ? （9）

[max? f=1-i=1n-1（Q實，i+1-Qi+1）2i=1n-1Q實，i+1-Q實，平均2]? ? ?（10）

（3）約束條件：

[0≤Ci≤1]? ? ? ? ? ? （11）

上述準則中，Q實，i+1和Q實，平均分別表示[i+1]時刻實測出流量和平均實測出流量;Ci為馬斯京根模型洪水演算系數;[n]為時刻數目。在遺傳算法中，初始種群數量設置為500，交叉概率為0.8。

3.2參數率定

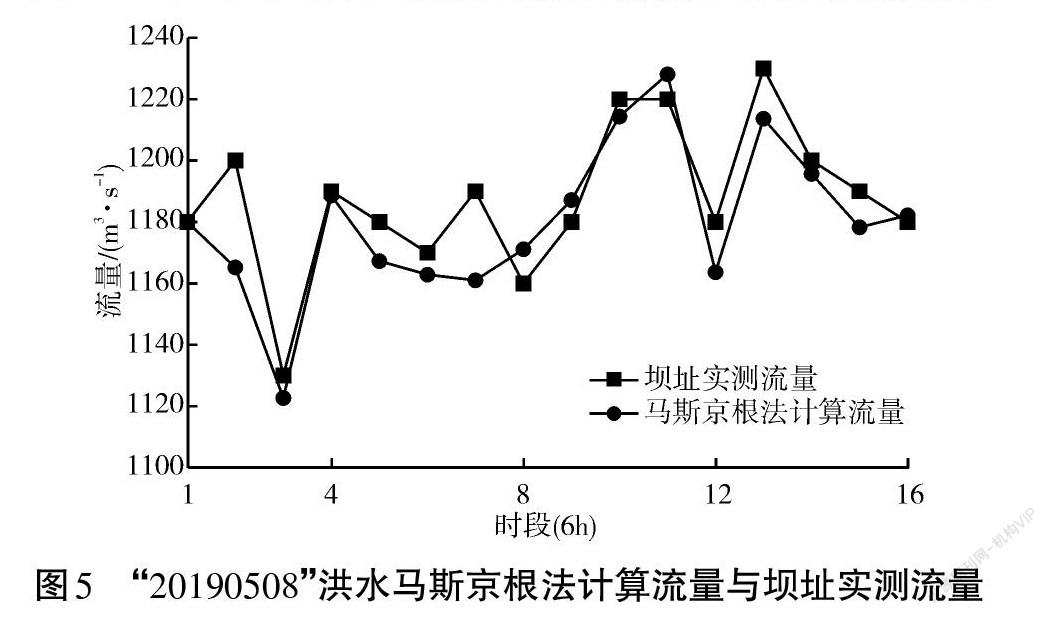
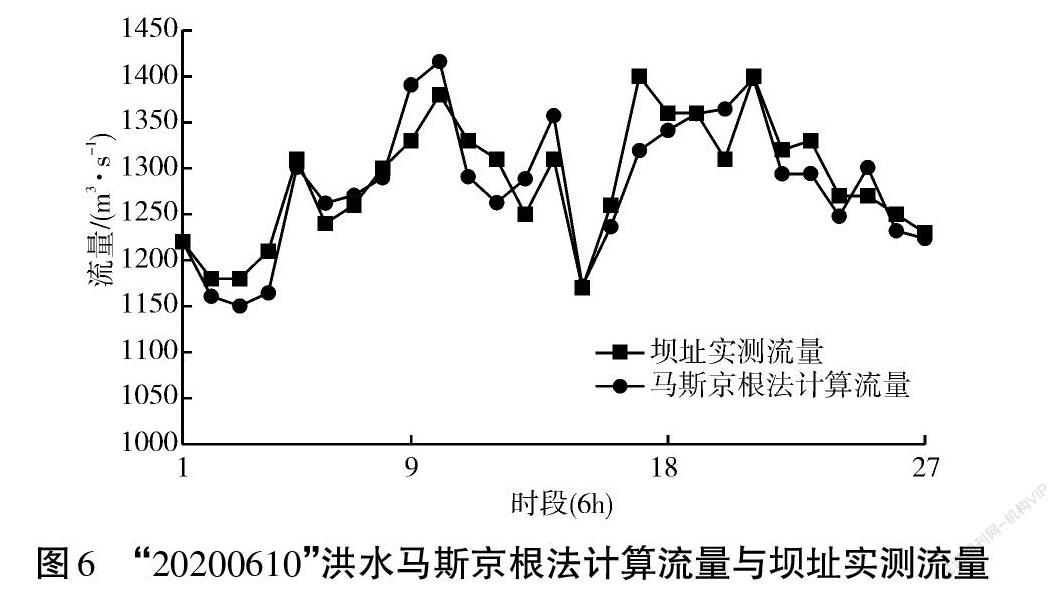
根據上述介紹的模型與算法，結合吉拉姆河流域“20180404”“20190508”和“20200610”洪水資料，對查特卡拉斯站河段至卡洛特專用站河段洪水馬斯京根模型參數進行率定。利用遺傳算法對馬斯京根法進行參數率定，結果見表1～2，圖4～6。

由表1馬斯京根法參數率定結果對查特卡拉斯河段洪水進行演算，由表2和圖4～6可得模擬洪水洪峰平均絕對誤差為14 m3/s，平均相對誤差為1.72%，平均納什系數為0.73。結果表明，計算洪水與實測洪水的洪峰和峰現時間誤差較小，洪水擬合度較好。

3.3 參數驗證

利用“20180316”洪水和“20200419”洪水對上節計算的查特卡拉斯河段至卡洛特壩址河段馬斯京根模型參數進行驗證。驗證結果見表3、圖7～8。

從表3、圖7和圖8可以看出，采用遺傳算法對馬斯京根法洪水演算模型參數進行驗證，并計算下游流量，所得演算結果與實測下游流量比較接近，洪峰差值分別為21 m3/s和238 m3/s，相對誤差分別為5.11%和14.08%，峰現時間一致，納什系數分別為0.81和0.83。其中，“20200419”洪水模擬結果偏小，這可能與查特卡拉斯河段至卡洛特壩址河段區間有降雨有關，且卡洛特水電站壩址實測洪水中包含區間產流。結果表明，遺傳算法作為模擬優化方法使用簡單、優化性能優異，具有較大的應用價值。

4 結 論

采用遺傳算法對馬斯京根洪水演算模型進行參數估計，計算下游流量，以模擬結果與實測值的誤差最小作為優化目標，獲得最優參數和下游流量。結論如下：

（1）與傳統方法（試算法等）相比，應用遺傳算法計算馬斯京根洪水演算模型參數節省了大量試算工作，且計算精度較高。

（2）在巴基斯坦吉拉姆河流域查特卡拉斯站至卡洛特水電站壩址河段，基于遺傳算法的馬斯京根洪水演算模型能較好計算壩址流量過程，洪峰誤差較小，峰現時間基本一致，流量過程擬合度較好。

（3）馬斯京根洪水演算模型可為卡洛特水電站水情預報發揮重要作用，為工程防洪度汛及下閘蓄水提供科學數據支撐。

參考文獻：

[1] 王夢娜，王秋萍，王曉峰. 灰狼優化算法在馬斯京根模型參數估計中的應用[J]. 計算機系統應用，2018，27（12）：198-203.

[2] 李德龍，程先云，楊浩，等. 人工智群算法在水文模型參數優化率定中的應用研究[J]. 水利學報，2013，44（增1）：95-101.

[3] 王金陽，郭承軍，黃曼娜. 改進蛙跳算法的約束處理方法[J]. 仲愷農業工程學院學報，2017，30（1）：48-52.

[4] 金菊良，丁晶. 遺傳算法及其在水科學中的應用[M]. 成都：四川大學出版社，2000.

[5] 金羽.? 淮河流域并聯水庫群防洪錯峰優化調度研究[D]. 南京：河海大學，2007.

[6] 左廣巍.? 河道洪水演算方法的研究與應用[D]. 武漢：華中科技大學，2004.

[7] 劉啟松，鄧頌霖，徐志，等.? 巴基斯坦卡洛特水電站實時洪水預報系統設計及運用[J].? 水利水電快報，2020，41（7）：5-8.

[8] 鄢雙紅.? 巴基斯坦卡洛特水電站工程特點及關鍵技術[J].? 水利水電快報，2020，41（1）：36-41.

[9] 劉啟松，鄧頌霖，徐志，等.? 臨近流域替代法在巴基斯坦卡洛特水電站壩址洪峰流量預報中的應用[J].? 水利水電快報，2020，41（4）：12-15.

[10] 鄧頌霖，徐志，劉啟松，等.? 地貌單位線在卡洛特水電站洪水預報中的運用[J].? 水資源研究，2019（6）：611-617.

[11] 李明明，李乘軍，張銘. 改進PSO法在馬斯京根模型參數估計中的應用[J]. 人民長江，2008，39（3）：60-62.

[12] 王文川，徐冬梅，邱林. 差分進化算法在馬斯京根模型參數優選中的應用[J]. 水利科技與經濟，2009，15（9）：756-758.

[13] 孟凱露，尚俊娜，岳克強. 混合蛙跳算法的最優參數研究[J]. 計算機應用研究，2019（11）：1-7.

[14] 劉攀，郭生練，李瑋，等.? 用多目標遺傳算法優化設計水庫分期汛限水位[J].? 系統工程理論與實踐，2007，27（4）：81-90.

[15] 劉啟松.? 非一致性條件下水庫單值汛限水位優化設計[D].? 西安：西安理工大學，2018.

[16] 盧華，劉福勝，王少杰，等.? 基于遺傳算法的平原水庫壩高優化[J].? 人民黃河，2011，33（1）：125-126，128.

[17] 溫進化，陸列寰，何江波，等.? 基于遺傳算法的梯級水庫優化調度圖研究[J].? 安徽農業科學，2011，39（31）：19640-19642.

[18] 鐘平安，唐林.? 水庫優化調度遺傳算法參數的靈敏性分析[J].? 水力發電，2010，36（11）：13-16.

（編輯：李 慧）

Research on application of Maskingum model based on genetic algorithm

in Jhelum River Basin， Pakistan

LIU Qisong，LIU Tianyong，DENG Songlin

（Jingjiang Bureau of Hydrology and Water Resources Survey， Bureau of Hydrology， Changjiang Water Resources Commission， Jingzhou 434000， China）

Abstract： The Maskingum method is an important method for river flood forecasting and its calibration of parameters and coefficients is the key point， which directly affects the forecast accuracy. On the basis of elaborating the basic ideas and performance analysis of genetic algorithm and by setting the goal of minimizing the error between the simulation results and the measured value， the coefficients of the Maskingum method was searched directly and the relation equation of upstream and downstream flows? was obtained. The flood process from Chattarkallas to Karot Hydropower Station on Pakistan's Jhelum River? was researched. The average absolute error of the genetic algorithm was 60.2 m3 /s， the average relative error was 4.87%， and Nash coefficient was 0.77. The results showed that the genetic algorithm was effective in the parameter optimization of the Maskingum model. The simulation accuracy of flood from Chattarkallas to Karot Hydropower Station on Pakistan's Jhelum River was high， which can provide technical support to flood forecast of Karot Hydropower Station.

Key words：flood forecast;genetic algorithm;Maskingum model;Jhelum River Basin; Karot Hydropower Station; Pakistan