多光伏發電單元并入弱交流電網系統的站內/站網次同步振蕩特性分析

趙書強，高瑞鑫，邵冰冰，龍鑫，孫夢雪，李思妍

(河北省分布式儲能與微網重點實驗室(華北電力大學)，河北省保定市 071003)

0 引 言

根據國際可再生能源機構統計，2020年全球光伏新增裝機127 GW，累計裝機容量達到733 GW。我國光伏新增裝機48.2 GW，位列全球第一[1]。太陽能作為一種清潔、可再生的能源，在我國的能源戰略中越來越受到重視[2]，光伏發電的開發也呈現“規模化分散開發、低壓接入、就地消納”以及“大規模集中開發、中高壓接入、高壓遠距離外送消納”兩種方式并存格局[3]。

然而，我國太陽能發達地區和負荷中心呈逆向分布，光伏電能的高壓遠距離外送成了必要，但遠距離的電能輸送也使得光伏電站與大電網之間的連接變得較為薄弱[4]。當交流電網較弱時，規模化光伏發電的集中并網有可能引發系統的次同步振蕩(sub-synchronous oscillation, SSO)，威脅系統的安全穩定運行[5]。

目前，新能源并網SSO事故主要出現在風電并網系統中。2012年以來，我國張北地區發生了多起雙饋風電機組經串補并網SSO事故[6]。2015年，我國新疆哈密地區發生了永磁直驅風電機組并入弱交流電網SSO事故[7]，引起了學術與工程界的廣泛關注。因此，現有的新能源機組并網穩定性問題的研究主要集中在風電[8-11]，對光伏并網穩定性的研究較少。

研究光伏并網穩定性的方法主要分為阻抗法和特征值分析法。基于阻抗分析法，現有研究主要分析交流電網對光伏并網系統穩定性的影響。文獻[12-13]分析了電網阻抗對大型光伏電站并網系統穩定性的影響。文獻[14]定量分析了并網逆變器與弱電網之間由于阻抗交互影響所產生的諧波振蕩。文獻[5]建立了光伏并網系統阻抗模型，基于阻抗分析法，分析了光伏并入弱交流電網系統發生SSO的機理，同時分析了控制器參數對SSO的影響。

基于特征值分析法，現有研究主要分析光伏系統參數對其小干擾穩定性的影響。文獻[15]對光伏發電系統穩定性進行了分析，并提出了一種全局優化的控制器參數設計方法。文獻[16-17]建立了光伏發電并網系統的小信號模型，分析了控制器參數對系統穩定性的影響。文獻[18]分析了電網強弱和鎖相環參數對光伏發電并網系統穩定性的影響。文獻[15-18]均將光伏電站等值為一個發電單元進行光伏發電并網系統穩定性分析，但單發電單元等值系統無法考慮光伏電站內部各發電單元之間的交互作用，具有一定局限性。

目前，鮮有文獻使用多發電單元的等值模型研究光伏電站并入弱交流電網的穩定性。文獻[19]基于2個光伏發電單元并聯接入電網的數學模型，得到了2個發電單元的輸出有功功率關于系統參數的耦合關系代數式，指出了多光伏發電單元間功率環路存在耦合項，且易受光伏發電單元運行工況與鎖相環控制器比例系數的影響。文獻[20]指出多直驅風機經柔直并網系統存在風電場內多機交互作用產生的場內SSO模式，以及風電場與柔直系統交互作用產生的場網SSO模式。由于光伏與直驅風機的并網接口具有較高的一致性[21]，當所連交流電網較弱時，光伏電站內也有可能出現多個發電單元交互作用產生的站內SSO模式。同時，考慮站內/站網2種SSO模式對于光伏發電單元參數變化存在阻尼耦合，如果阻尼耦合的趨勢趨反，通過優化單個等值發電單元并入弱交流電網的發電單元參數來抑制站網SSO時，就有可能激發嚴重的站內SSO。因此，有必要建立多光伏發電單元等值模型并研究光伏電站并入弱交流電網系統的站內/站網SSO特性。

本文首先建立三發電單元光伏電站并入弱交流電網系統的52階小信號模型，通過特征值法得到系統中存在的SSO模式及相關參與因子；其次，研究光伏發電單元的參數變化對站內/站網SSO模式阻尼耦合特性的影響；最后，通過時域仿真驗證理論分析結果的正確性。

1 光伏電站并網系統

本文建立的單級式三光伏發電單元電站等值模型如圖1所示。光伏電站中包括3個采用參數聚合等值的發電單元[22]，每個發電單元由40個容量為500 kW的光伏陣列聚合而成，所發電量通過逆變器和LCL型濾波器后經變壓器T1一次升壓匯入35 kV匯流線，隨后由變壓器T2二次升壓至110 kV后經并網線路(等效為一條線路)接入主網(等效為理想電源)。

對于第n個發電單元，CDCn為逆變器直流側電容；Lf1n、Lf2n、Cfn為LCL型濾波器的2個濾波電感及濾波電容；k1n為變壓器T1的變比；Cn、Rn、Ln分別為匯流線路對地電容、電阻、電感；ipvn為光伏陣列的輸出電流；idcn、ikn、ign、in分別為逆變器輸入電流、逆變器輸出電流、濾波器出口處電流及匯流線路電流；uDCn、ukn、ujn、ugn分別為逆變器輸入電壓、逆變器出口電壓、濾波電容處電壓、變壓器T1低壓側電壓；Pn為發電單元匯入公共耦合點(point of common coupling, PCC)有功功率。

對于交流電網，Cs、Rs、Ls分別為并網線路對地電容、電阻、電感；k2為變壓器T2的變比；is為并網線路電流；e、us分別為PCC電壓與交流電網電壓；PPV為光伏電站并網有功功率。

在圖1中，交流系統強度用短路比(short circuit ratio, SCR)KSCR描述，即交流系統短路容量Sac與光伏電站額定功率SN之比[19]。

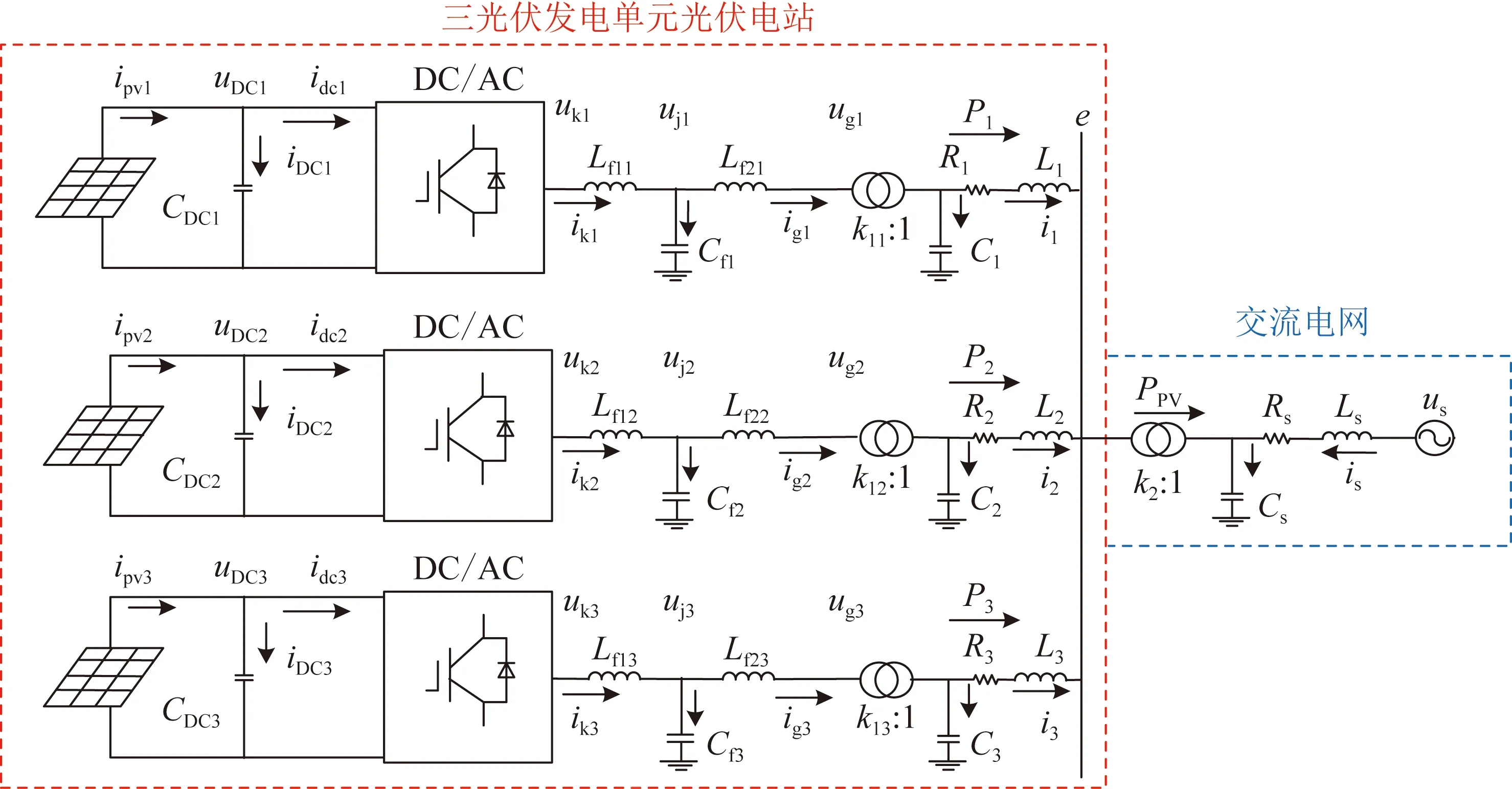
圖1 三光伏發電單元并網系統結構Fig.1 Structure of grid-connection system of three PV generation units

(1)

式中：Zs為電網等值阻抗；UN為電網電壓的額定值。SCR越大，交流系統越強，SCR介于2～3之間時，系統為弱交流系統。

系統的控制電路包括逆變器控制器和鎖相環控制器。其中，逆變器控制結構如附圖A1所示，鎖相環控制結構如附圖A2所示。

2 光伏電站并網系統小信號模型

對于圖1所示的三光伏發電單元并網系統拓撲結構，將系統分為4個主要模塊進行建模，包括光伏電池建模、站內主電路建模、站內控制電路建模與并網線路建模，整合后得到全系統的小信號模型。

2.1 光伏電池

本文采用光伏電池的工程模型[23]，如式(2)所示。

(2)

式中：Ipv為輸出電流；Upv為輸出電壓；Imref為最大功率點電流；Umref為最大功率點電壓；T為實際空氣溫度；Tref為空氣溫度參考值；F為實際光照強度；Fref為光照強度參考值；a、b、c為補償系數。

2.2 站內主電路狀態方程

站內主電路狀態方程由逆變器直流側穩壓電容、LCL型濾波器和匯流線路的狀態方程構成，各狀態變量如表1所示。

直流側穩壓電容CDC的狀態方程為：

(3)

表1 光伏電站主電路狀態變量Table 1 State variables of main circuit of PV plant

選擇d-q-0坐標系為基于節點g電壓矢量定向的同步旋轉坐標系，使得uqg=0。根據瞬時功率理論[24]，系統瞬時有功功率p、無功功率q分別為p=1.5udgidg，q=1.5uqgiqg，若忽略電力電子器件和逆變器的功率損耗則有idc=1.5udgidg/uDC。

LCL濾波器的狀態方程為：

(4)

匯流線路狀態方程為：

(5)

式中：ed、eq分別為PCC處的d、q軸電壓。

2.3 站內控制電路狀態方程

控制器的狀態方程包括逆變器控制器和鎖相環控制器狀態方程，各狀態變量如表2所示。

表2 光伏電站控制器狀態變量Table 2 State variables of PV plant controller

逆變器控制器狀態方程為：

(6)

式中：kpj、kij分別為逆變器的比例、積分系數，j=1，2，3；下標ref為相關狀態變量的參考值。

鎖相環控制器狀態方程為：

(7)

式中：kppll、kipll分別為鎖相環的比例、積分系數；ω0取基準角速度，ω0=2πf0，f0=50 Hz；θ為鎖相環的輸出角度。

2.4 并網線路狀態方程

光伏電站并網線路的狀態變量如表3所示。

表3 光伏電站并網線路狀態變量Table 3 State variables of PV plant grid-connection lines

并網線路狀態方程為：

(8)

式中：idl、iql為3個光伏發電單元匯流線路d、q軸電流之和。

2.5 全系統的小信號模型

結合上述光伏電站和并網線路各模塊的狀態方程，可以得到三光伏發電單元并網系統的全階數學模型，經過線性化后可得到用于分析系統穩定性的小信號模型，如式(9)所示：

(9)

式中：Δx為線性化后的狀態變量；Δu為線性化后的輸入變量；A為狀態矩陣；B為輸入矩陣。

基于上述分析，單個光伏發電單元共有16個狀態變量：xPVn=[x1n、x2n、x3n、xan、xbn、uDCn、udjn、uqjn、udgn、uqgn、idkn、iqkn、idgn、iqgn、idn、iqn],其中n表示第n個發電單元。并網線路有4個狀態變量：xGrid=[ids、iqs、ed、eq]。因此，三光伏發電單元并網系統共有52個狀態變量:x=[xPV1,xPV2,xPV3,xGrid]。

3 系統SSO特性分析

基于第2節提出的小信號模型，首先利用特征值法分析三光伏發電單元并網系統中存在的SSO模式。同時，通過對各SSO模式進行參與因子分析，辨識出各SSO模式的主導狀態變量。最后，在PSCAD/EMTDC中搭建時域仿真模型，驗證理論分析結果的正確性。

3.1 特征值分析

設置3個發電單元運行工況、初始參數相同，小信號模型中各參數如附表A1所示。

此時，3個發電單元的有功電流內環比例系數kp2取為0.025。由系統的狀態矩陣A計算得到三光伏發電單元并網系統中存在的振蕩模式。其中，SSO模式的特征值、振蕩頻率和阻尼比如表4所示。

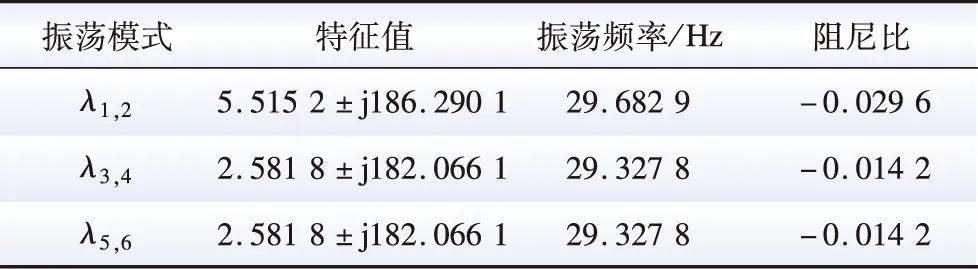
表4 三光伏發電單元并網系統的SSO模式 (kp2=0.025)Table 4 SSO mode of PV grid-connection system with three PV generation units (kp2=0.025)

由表4可知，三光伏發電單元并網系統的SSO模式有3個，分別為λ1,2、λ3,4、λ5,6，振蕩頻率分別為29.682 9、29.327 8、29.327 8 Hz。3個SSO模式對系統都呈現負阻尼，說明在該算例下，這3個SSO模式是不穩定的，對系統穩定性的影響不利。

3.2 參與因子分析

為了進一步研究系統中各狀態變量與3個SSO模式之間的關系，分別計算3個SSO模式λ1,2、λ3,4、λ5,6的歸一化參與因子，如圖2所示。為方便分析，將52個狀態變量進行編號。其中，1—16、17—32、33—48分別為第一、二、三發電單元的狀態變量，49—52為交流電網的狀態變量。

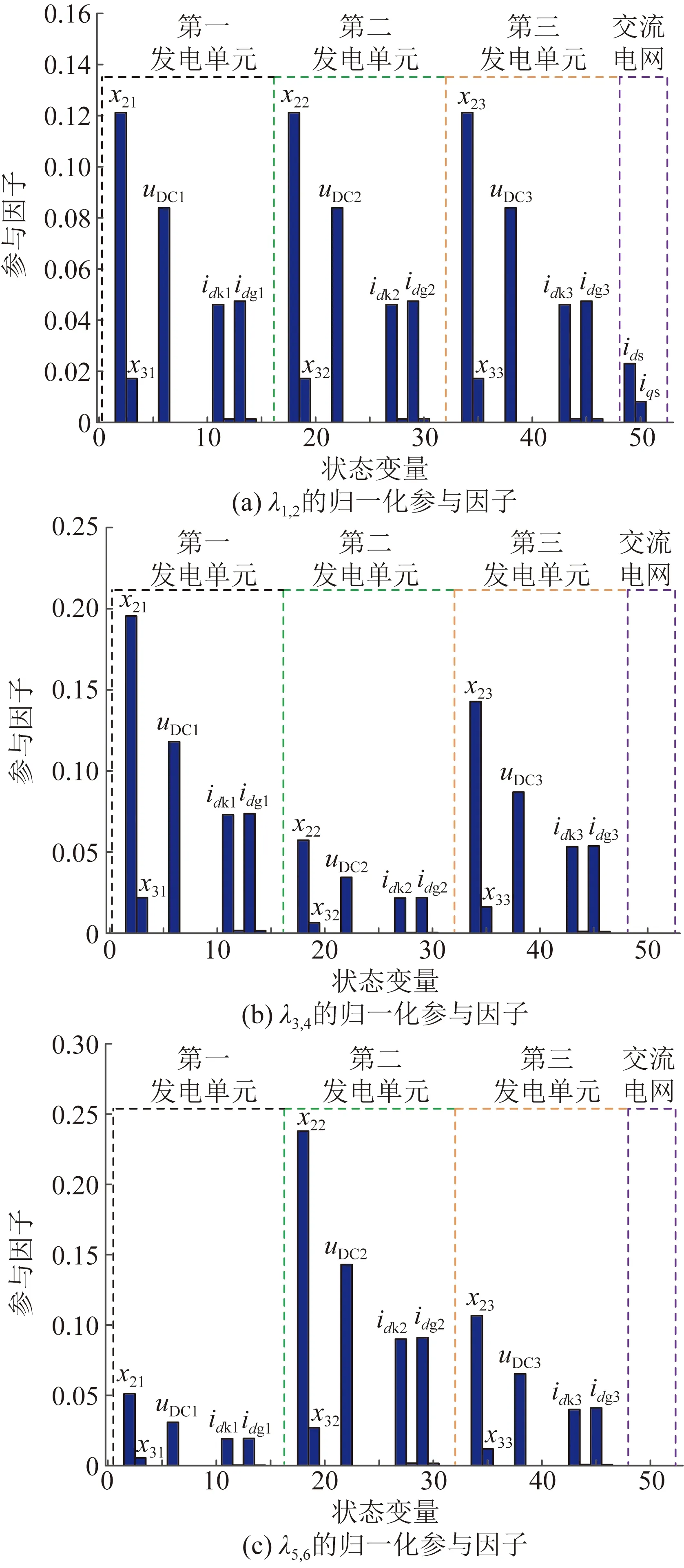
圖2 光伏并網系統SSO模式歸一化參與因子Fig.2 Normalized participation factor of SSO mode of PV grid-connection system with three PV generation units

由圖2可知，參與SSO模式λ1,2的狀態變量主要有3個發電單元中的x2n、x3n、uDCn、idkn、idgn(n=1,2,3)和交流系統中的ids，iqs，即SSO模式λ1,2是3個發電單元與交流電網之間的交互作用引起的SSO。參與SSO模式λ3,4和SSO模式λ5,6的狀態變量主要有x2n、x3n、uDCn、idkn、idgn(n=1,2,3)，即SSO模式λ3,4和SSO模式λ5,6是光伏電站內部3個發電單元之間交互作用引起的SSO。

綜合上述分析，SSO模式λ1,2是以3個發電單元中的直流電壓控制環節、有功電流內環控制環節和交流電網為主導環節的站網振蕩模式SSO1。SSO模式λ3,4和SSO模式λ5,6是以3個發電單元中直流電壓控制環節和有功電流內環控制環節為主導環節的站內振蕩模式SSO2。

3.3 時域仿真驗證

為了驗證表4中對系統SSO模式分析的正確性，基于PSCAD/EMTDC搭建圖1所示的三發電單元光伏并網系統的時域仿真模型。在t=2.30 s時，同時將3個發電單元的有功電流內環比例系數kp2由0.250改變為0.025，系統各參數與附表A1中的參數相同。得到3個發電單元匯入PCC點的有功功率P1、P2、P3和整個光伏電站的并網有功功率PPV的變化曲線，如圖3、4所示。

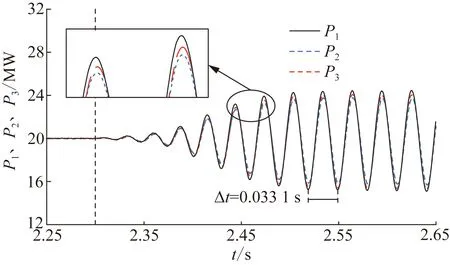
圖3 各發電單元匯入PCC點有功功率Fig.3 The active power of each PV generation unit

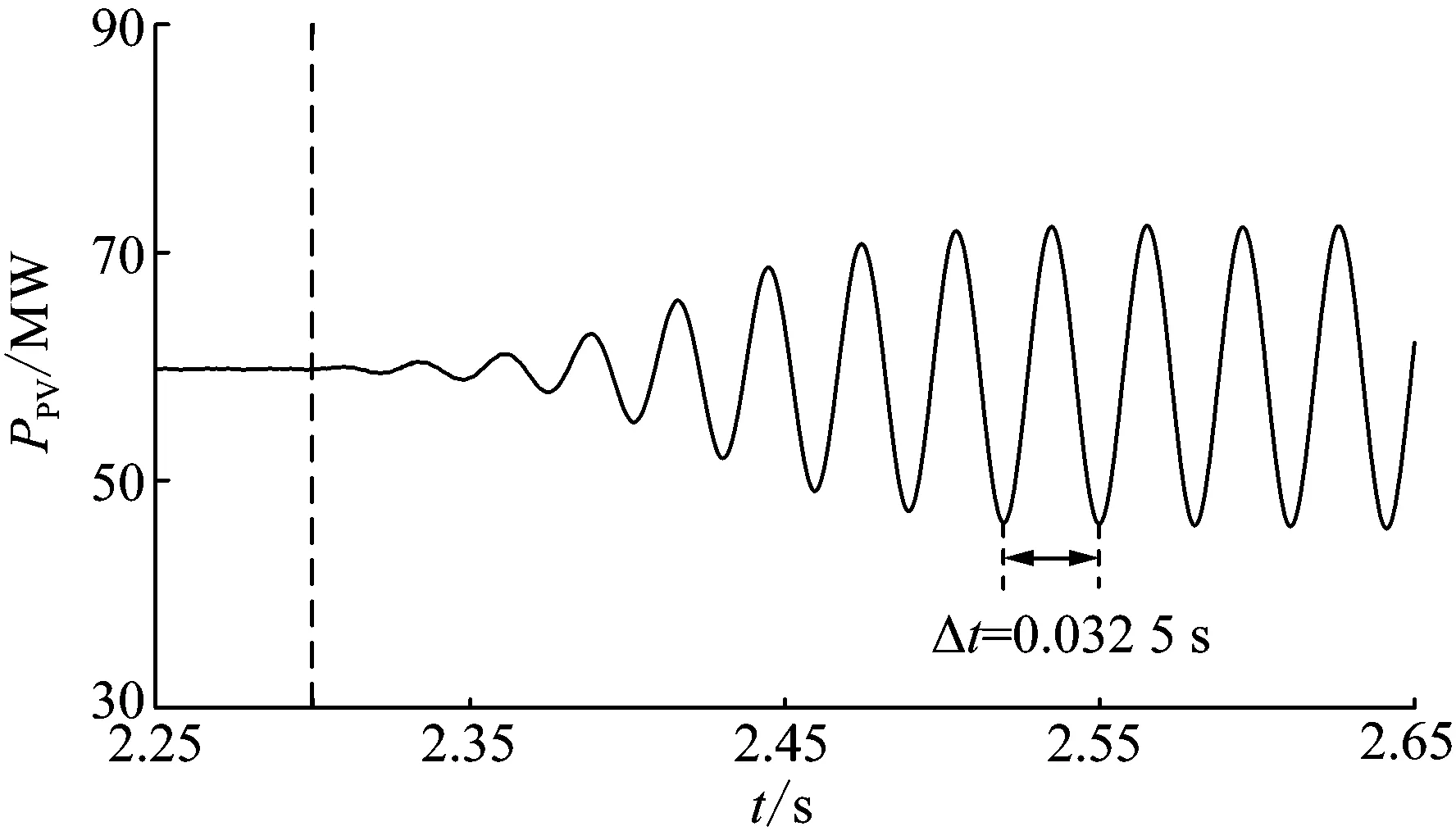
圖4 光伏電站的并網有功功率Fig.4 Active power of grid-connected PV plant

由圖3、4可知，在t=2.30 s時，系統受到干擾后，各個發電單元匯入PCC點的有功功率P1、P2、P3均出現了頻率為30.21 Hz左右的SSO，振蕩頻率與表4中的站內SSO模式λ3,4和SSO模式λ5,6的振蕩頻率相近，且P1、P2、P3的振蕩幅值不完全相同，說明此時系統發生了站內SSO。同時，整個光伏電站的并網有功功率出現了頻率為30.77 Hz左右的SSO，振蕩頻率與表4中的站網SSO模式λ1,2振蕩頻率相近。因此，通過該時域仿真結果驗證了三光伏發電單元并網系統特征值分析結果的正確性。

4 站內/站網SSO阻尼耦合特性分析

由上文的參與因子分析可知，站內/站網SSO模式均受發電單元參數的影響。因此，在發電單元的參數發生變化時，2種SSO模式之間將存在阻尼耦合。若阻尼耦合趨反，在抑制站網SSO時就可能激發站內SSO。因此，本節分析光伏發電單元參數變化對站內/站網SSO模式阻尼耦合特性的影響。

分別設置發電單元的直流電容CDC、有功電流內環比例系數kp2、積分系數ki2、發電容量改變，通過特征值分析法，得到系統2種SSO模式下的特征值實部變化情況，進而分析光伏發電單元參數變化對2種SSO模式阻尼耦合特性的影響。

4.1 直流電容參數的影響

設置3個發電單元的直流電容CDC參數在[0.5CDC0，4CDC0](CDC0為CDC的初始值)范圍內變化，保持其余參數不變，2種SSO模式的特征值實部隨CDC的變化曲線如圖5所示。

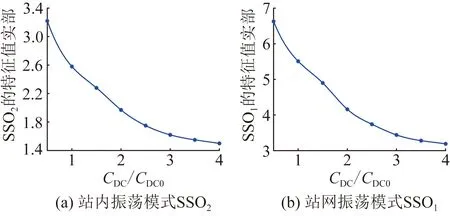
圖5 系統SSO模式特征值實部隨CDC的變化曲線Fig.5 The variation curve of the real part of the eigenvalue of the system SSO mode with the CDC

由圖5可知，站內/站網SSO模式的特征值實部均隨著CDC的增大而減小，系統的阻尼增強。因此，站內/站網2種SSO模式對CDC參數的變化阻尼耦合趨同，在保持系統穩定的情況下，適當增大CDC可以提高系統SSO模式的阻尼。

進行3組時域仿真驗證，設置3組仿真中的CDC參數分別為0.5CDC0、CDC0和3CDC0，保持其他參數不變。在t=2.30 s時，令kp2由0.250變為0.025。觀察各個發電單元匯入PCC點有功功率(取P1為例)、光伏電站并網有功功率的變化，如圖6所示。

由圖6(a)、(b)，對比3組CDC參數下的SSO波形可知，隨著CDC參數的增大，第一發電單元匯入PCC點的有功功率P1與光伏電站并網有功功率PPV的發散程度均減慢。因此，隨著CDC參數的增大，站內/站網SSO阻尼均增大，驗證了圖5及其理論分析的正確性。

圖6 系統有功功率隨CDC的變化曲線Fig.6 The variation curve of system active power with CDC

4.2 有功電流內環控制器參數的影響

設置3個發電單元的有功電流內環比例系數kp2在[1.0kp20, 4.5kp20](kp20為kp2的初始值)范圍內同時變化，積分系數ki2在[1.0ki20, 4.5ki20](ki20為ki2的初始值)范圍內同時變化，均保持其余參數不變。得到系統2種SSO模式下的特征值實部隨kp2、ki2的變化曲線，如圖7所示。

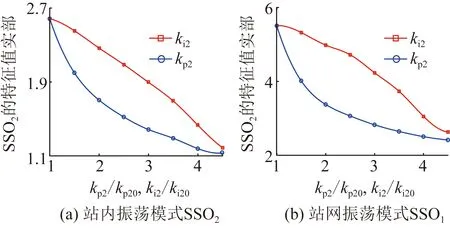
圖7 系統SSO模式特征值實部隨kp2、ki2的變化曲線Fig.7 The variation curve of the real part of the eigenvalue of the system SSO mode with the kp2、ki2

由圖7可知，在2種SSO模式下，系統特征值實部隨kp2與ki2的變化趨勢大致相同，均隨kp2、ki2的增大而減小，系統阻尼增強。因此，站內/站網2種SSO模式對有功電流內環參數的變化阻尼耦合趨同，在保持系統穩定的情況下，可適當增大kp2、ki2以提高系統SSO模式的阻尼。

進行時域仿真驗證，在t=2.30 s時，令kp2由0.250變為0.025，ki2仍為初始值，在t=3.00 s時，保持kp2不變，令ki2由20變為200。觀察各個發電單元匯入PCC點有功功率(取P1為例)、光伏電站并網有功功率變化及頻譜分析結果，如圖8所示。

由圖8(a)、(b)可知，2種SSO模式體現的阻尼耦合特性趨同。t=2.30 s時，kp2的減小引發了系統站內/站網SSO，說明kp2的減小將使系統的阻尼減弱。t=3.00 s時，ki2的增大使得站內/站網SSO開始衰減，說明在一定范圍內增大ki2可以增強系統的SSO模式阻尼，使系統更加穩定。

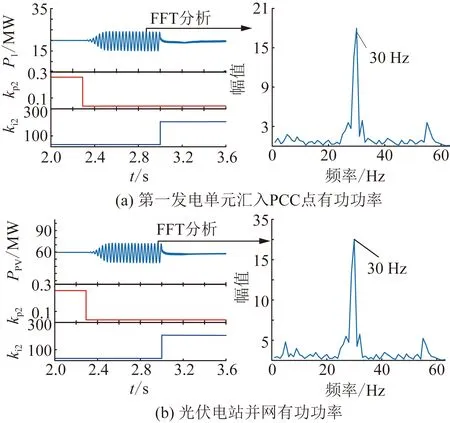
圖8 系統有功功率隨kp2、ki2的變化曲線及頻譜分析Fig.8 The variation curve of system active power with kp2、ki2 and the FFT analysis results

4.3 光伏發電單元發電容量的影響

考慮到實際工程中，光伏電站覆蓋面積較廣，不同區域的光伏陣列出力可能不同。因此，設置2種不同的工況以分析光伏發電單元容量變化對站內/站網SSO模式的阻尼耦合特性影響。

在工況1下，設置3個發電單元的發電容量S在[1.0S0, 2.0S0](S0為S的初始值)范圍內同時變化，保持其余參數不變；在工況2下，設置第一發電單元的發電容量為S0，第二、第三發電單元的發電容量S在[1.0S0，2.0S0]范圍內同時變化，保持其余參數不變。觀察2種SSO模式下的系統特征值實部隨S的變化，結果如圖9所示。

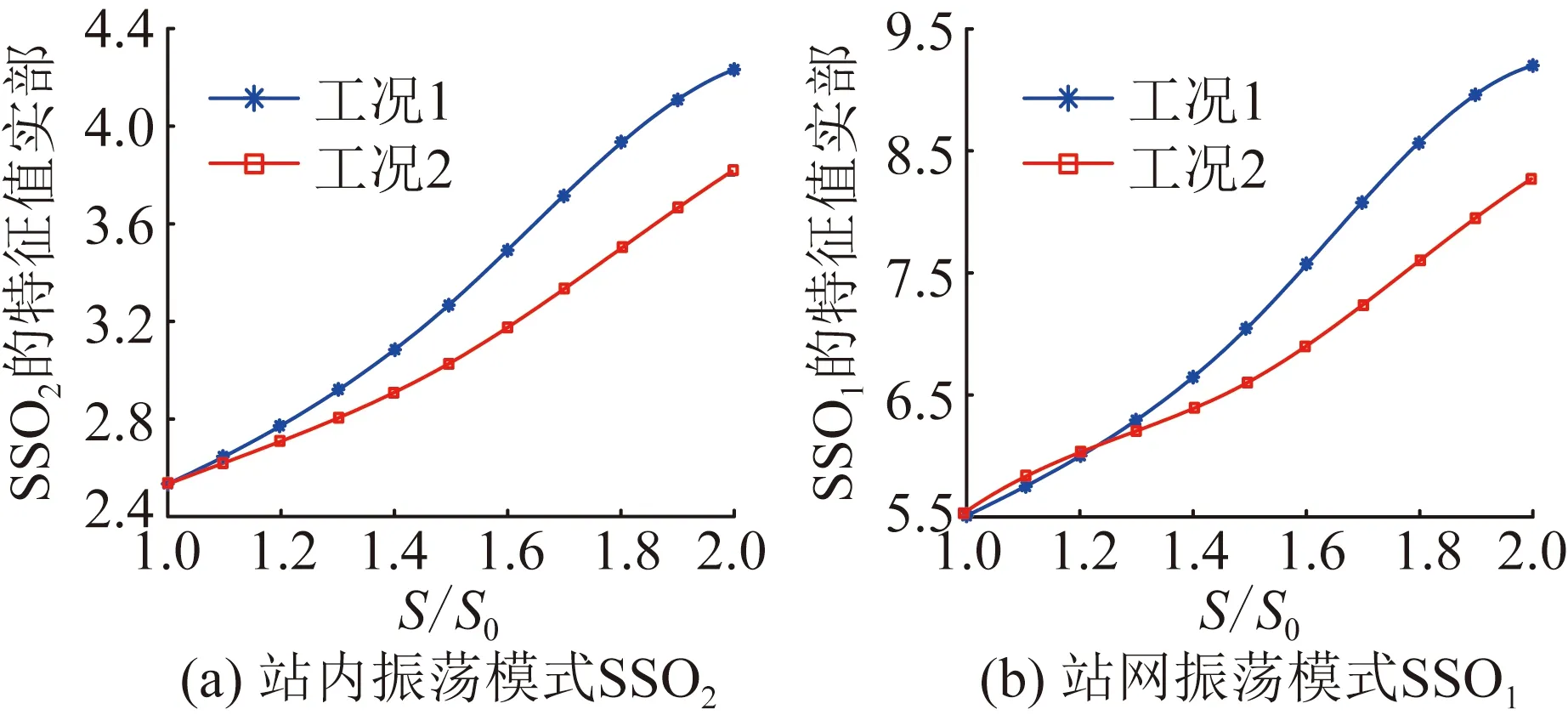
圖9 系統SSO模式特征值實部隨S的變化曲線Fig.9 The variation curve of the real part of the eigenvalue of the system SSO mode with S

由圖9(a)、(b)可知，當發電單元的發電容量增大時，2種工況下的站內/站網SSO系統特征值實部均增大，且工況1對特征值實部的影響程度大于工況2，系統阻尼逐漸減弱。因此，站內/站網2種SSO模式對單元發電容量的變化阻尼耦合趨同。

為了驗證圖9及其理論分析的正確性，對于工況2，進行3組時域仿真。保持3組仿真中第一發電單元容量為S0，再將3組中的第二、第三發電單元容量分別設置為1.25S0和1.50S0。在t=2.3 s時，令3組仿真的kp2由0.250變為0.025，得到第一發電單元匯入PCC點的有功功率和光伏電站并網有功功率變化曲線，如圖10所示。

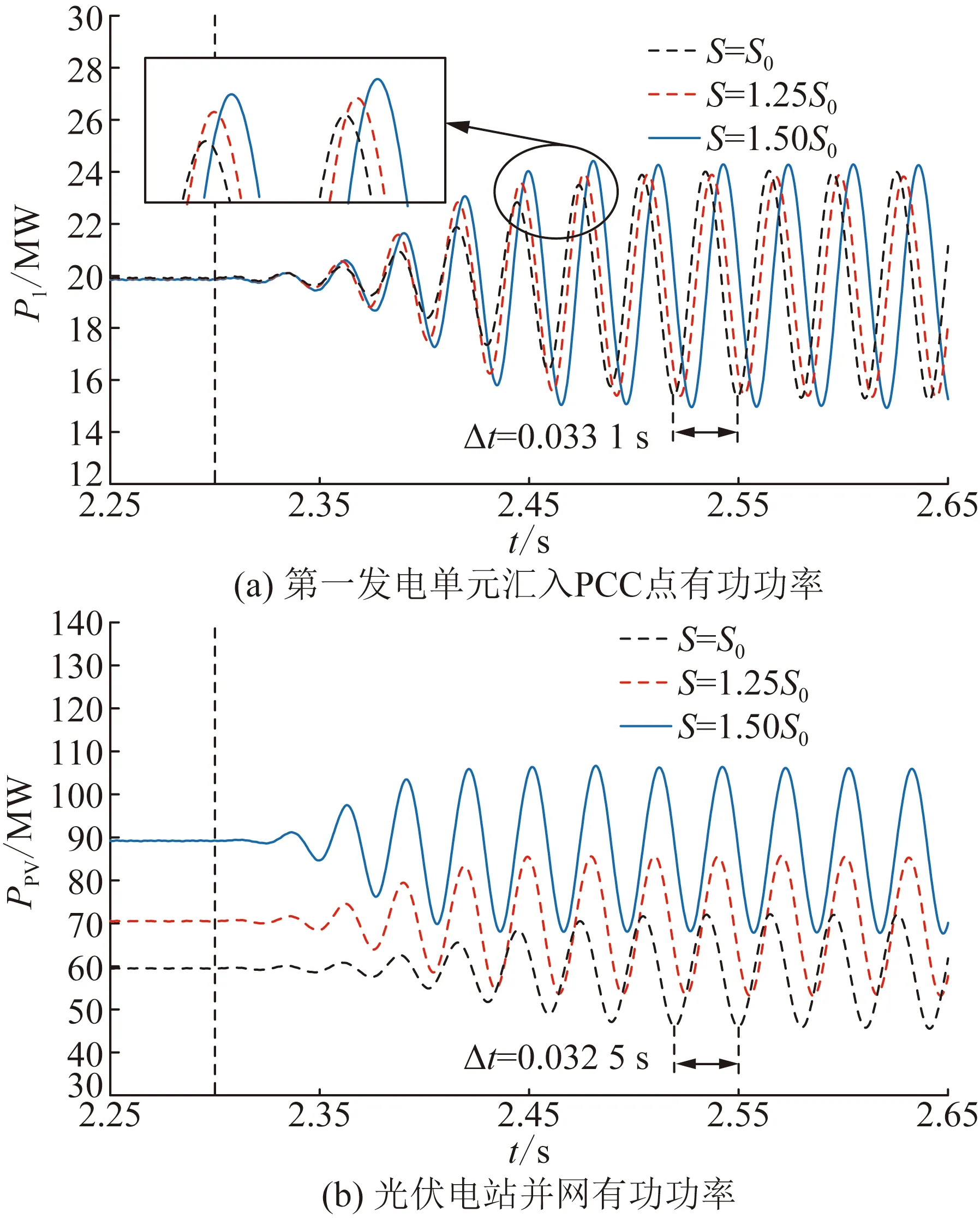
圖10 系統有功功率隨S的變化曲線Fig.10 The variation curve of system active power with S

由圖10(a)可知，雖然3組仿真下第一發電單元的容量均未改變，但隨著第二、第三發電單元容量的增大，在發生站內SSO時，P1的發散程度加快，說明3個發電單元之間存在交互作用使得站內SSO阻尼減小。由圖10(b)可知，隨著光伏電站發電容量的增大，在發生站網SSO時，PPV的發散程度加快，系統的站網SSO阻尼減小。驗證了圖9及其理論分析的正確性。

綜上所述，經過理論分析與時域仿真的驗證，站內/站網2種SSO模式對光伏發電單元的參數變化阻尼耦合趨同。

5 結 論

本文建立了三光伏發電單元并入弱交流電網系統的小信號模型，采用特征值法分析系統中存在的SSO模式，研究了光伏發電單元的參數變化對站內/站網SSO模式阻尼耦合的影響。主要結論如下：

1)三光伏發電單元并網系統中存在2個站內SSO模式和1個站網SSO模式。站內SSO模式由光伏電站內3個發電單元之間交互作用產生；站網SSO模式由3個發電單元與交流電網交互作用產生。

2)光伏并網系統站內SSO2模式的主導因素為直流穩壓電容、逆變器電流控制環節。站網SSO1模式的主導因素除了直流穩壓電容、逆變器電流控制環節外，還有交流電網的參與。

3)站內SSO2模式和站網SSO1模式對于光伏發電單元參數的變化阻尼耦合趨同。隨著發電單元發電容量S的不斷增大，系統的SSO阻尼逐步減弱，為系統的安全穩定運行帶來挑戰。相反的，在一定范圍內，適當增大直流側穩壓電容CDC、有功電流內環控制器的比例系數kp2、積分系數ki2都將提高系統的SSO阻尼，使系統穩定性提高。