基于平均-差異模型的電池組短路電流估計*

張 莉，高興奇，張健豪

（大連理工大學電氣工程學院，大連116000）

前言

電動汽車因電池故障導致安全問題頻發，因而制約電動汽車的發展，其中電池內短路是觸發電池熱失控的共性環節［1］，因此及時有效地檢測電池內短路對降低熱失控風險至關重要。但由于內短路的類型不同，其電壓和溫度信號的表現及發展速度各不相同，很難用一種模型或檢測方法表征，而常規基于閾值的檢測方法往往無法滿足快速性和可靠性的要求。

對汽車動力電池系統而言，主要是針對串聯電池組的短路故障進行診斷。目前診斷的主要方法有：（1）充放電時電路模型的預測值與測量值對比；（2）端電壓異常下降后回升；（3）辨識參數變化。

其中基于模型的診斷方法最為廣泛，當電池發生短路時，其SOC會異常下降。基于此，Yang等［2］利用拓展卡爾曼濾波法對電池組中每一節電池的SOC進行估計，可以較為準確估計短路電阻，但其計算量過大，實際無法使用。為減小計算量，Xu等［3］提出基于比例積分觀測器的短路電流估計方法，利用兩節電池進行短路診斷。該算法收斂性較好，但沒考慮模型的參數變化。Kong等［4］提出根據電池間剩余充電容量變化來檢測短路，該方法不需要電池的精確模型和迭代計算，但其精確度受高SOC時個體差異影響。總之為降低診斷算法的計算量，需對電池組進行篩選，同時可將正常電池的狀態作為基準，通過分析電池間差異來對短路進行診斷和量化。

為反映電池組內不一致，鄭岳久［5］提出電池組平均-差異模型，在此基礎上，有人利用最小二乘法［6］或低通濾波法［7］可獲得電池間的內阻和開路電壓差異，也有人利用卡爾曼濾波法對短路電池SOC［8］或SOC差［9］進行估計。但上述研究沒有對較嚴重短路時模型的準確度進行分析。另外還有學者利用電壓相關系數［10］和參數辨識［11-12］對短路時出現電壓先降落后回升的特性和參數變化進行檢測，將正常電池作為參考基準可以提高檢測的準確度。

綜上所述，以往的研究依據平均-差異模型，對較輕微的短路可以較好診斷，但未對較嚴重短路時模型的適用性進行研究。本文中對該模型的準確性進行了分析，并提出參數校正方法。為適應不同的短路阻值，提出多尺度估計方法，即利用短時尺度對嚴重短路電流進行快速估計，利用長時尺度來提高輕微短路時的估計精度，并分析了短路時模型的參數變化規律和影響因素，說明估計方法的合理性。

1 電池模型與參數辨識

1.1 電池模型

通常通過電池的等效電路模型可對電池電壓進行擬合，盡管可以用若干RC環節來模擬電池的極化，提高擬合精度，但RC環節過多易造成過擬合，物理意義不明確。同時由于電池短路時實際溫度變化大且電流的頻譜很廣，離線測試的結果無法反映實際參數，所以須進行參數在線辨識。為降低計算量，本文中選用1階RC等效電路模型來對電池進行建模。

對于串聯電池組，各節電池的正常工況電流是相同的，另外通過前期篩選，內阻等參數差異很小，且符合正態分布，故可以用電池組中各電池參數的平均值來代表電池組的狀態，將這樣的模型稱為平均電池模型，如圖1（a）所示。

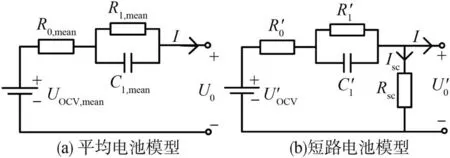
圖1 電池等效電路模型

圖中，UOCV，mean、R0，mean、R1，mean和C1，mean分別為平均開路電壓、歐姆電阻、極化電阻和電容，I和U0分別為電池工況電流和電壓。令τ=R1，meanC1，mean為時間常數，電池的端電壓與電流的關系為

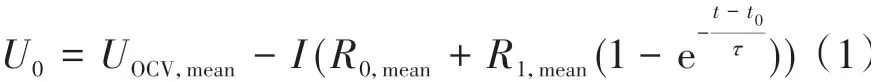
對于短路電池，其模型如圖1（b）所示，根據基爾霍夫定律，電池端電壓可表示為

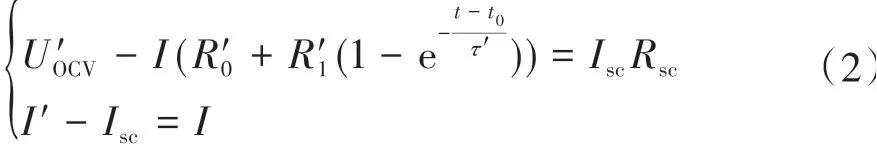
式中：U′OCV、R′0、R′1和C′1分別為短路電池開路電壓、歐姆電阻、極化電阻和電容；Isc和Rsc為短路電流和電阻。

由式（2）可得短路電流為

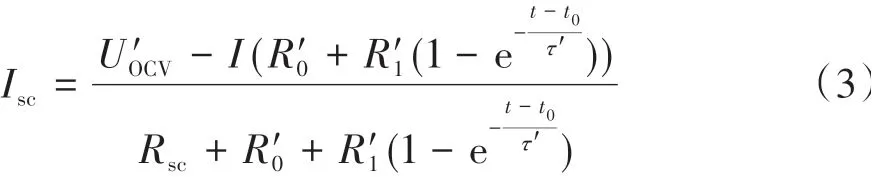
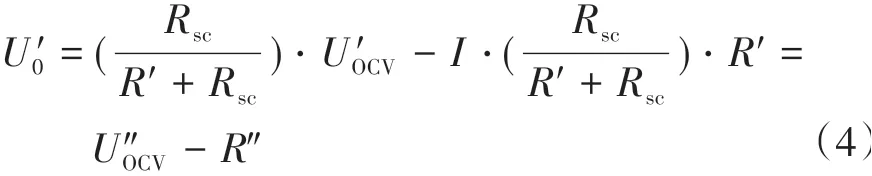
與式（1）對比可知，短路電池模型可等效為1階RC模型，但此時等效開路電壓U″OCV和等效參數R″是短路電池實際值的Rsc/(R′+Rsc)倍。當Rsc?R′時，該倍數影響較小，可忽略不計，但當兩者接近時，需要進行校正。由于電池工作時參數具有漸變性，可通過除以上一時刻的Rsc/(R′+Rsc)值對當前時刻參數進行校正，此時電流轉化為I′=I+Isc。將短路電池等效1階RC模型參數與平均模型參數的差值定義為電池差異模型，各參數定義為

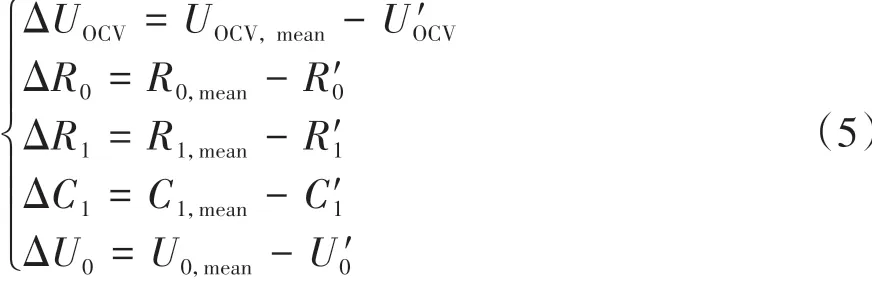
1.2 參數辨識

對于平均模型，需要辨識的參數有UOCV，mean和RC參數。前者可由SOC?OCV關系確定，SOC取電池組的平均值，由安時積分法獲得

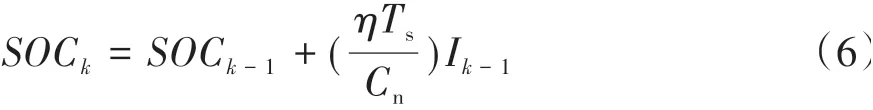
式中：η為充放電效率；Ts為采樣時間間隔；Cn為電池容量。

RC參數可由迭代最小二乘法在線辨識：

式中e(k)為y(k)的誤差，各項表達式為

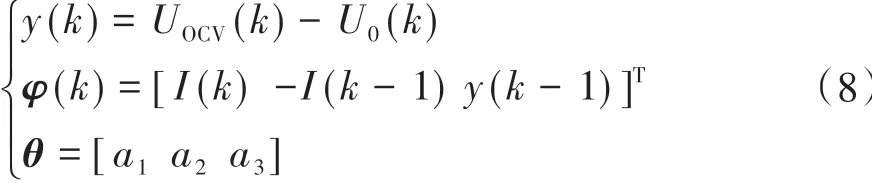
最小二乘迭代形式為

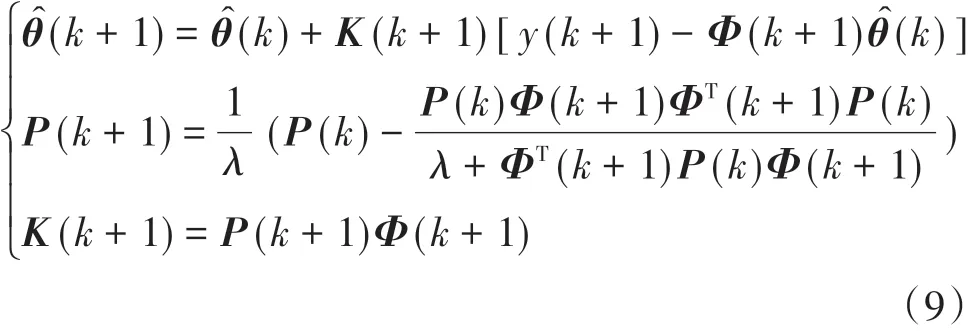
對于差異模型，電池之間的不一致性及參數變化具有低頻特性［5］，故可將待辨識量看作緩慢變化的狀態變量。本文利用卡爾曼濾波法對其進行參數辨識，建立狀態空間方程：

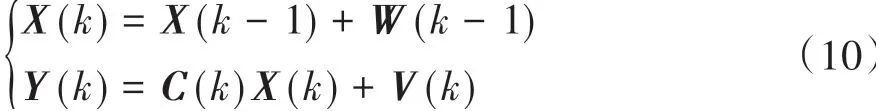
式中：狀態變量X=[b1b2b3b4]T，并對X進行相應轉換即可獲得對應參數；觀測矩陣C(k)=[1-I(k)I(k-1)-I(k)ΔU0(k)-ΔU0(k-1)]；輸出變量Y(k)=ΔU0(k)。W和V分別為過程噪聲和觀測噪聲。

卡爾曼濾波迭代形式為

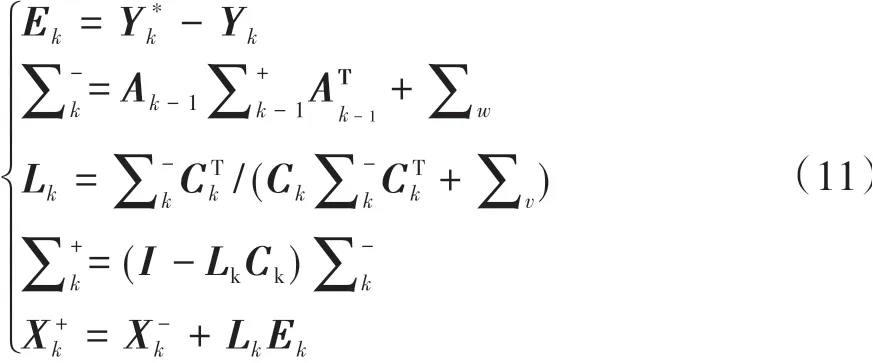
則參數校正的具體流程為

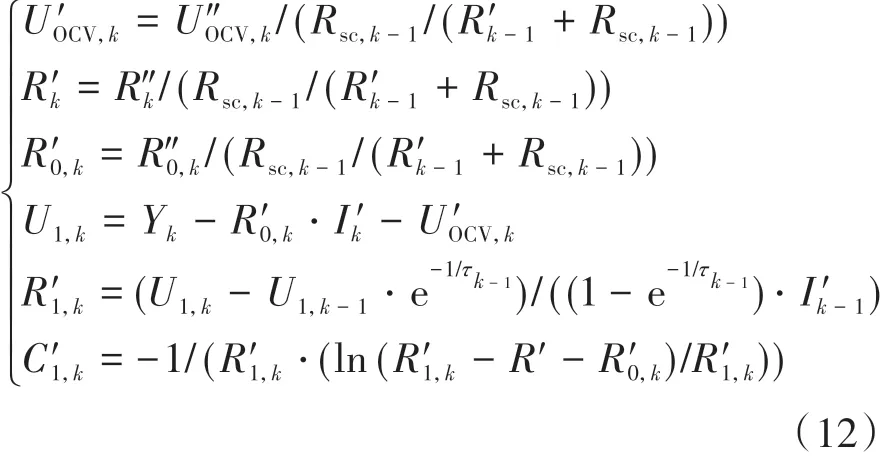
式中U1，k為極化電壓。

通過最小二乘法和卡爾曼濾波法的聯合估計，可以獲得差異模型的參數，隨后進行參數校正，進而利用式（5）獲得短路電池參數，最后利用f-1(UOCV)即可獲得短路電池的SOC。

2 短路電流估計與診斷策略

2.1 短路電流估計

電池開路電壓可看作由一個電容C產生［13］，其與電流和開路電壓的關系為

SOC定義的微分形式為

通過式（13）和式（14）消去電流I可得到電容與SOC的對應關系為

當電池的開路電壓轉化為可變電容C的電壓時，等效電路可表示為

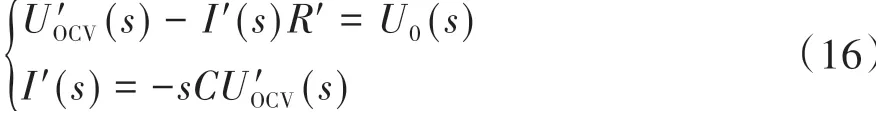
消去U′OCV可得到

轉換為離散形式：

由式（18）可知，利用電壓信號和RC參數即可對總放電電流進行估計。而電池的正常工況電流I是可測量的，兩者相減即可對短路電流進行估計，且端電壓除以短路電流即可獲得Rsc。

當短路電流較小時，由于采樣精度低，模型頻率響應差［13］以及參數和SOC的估計誤差等原因使電流誤差可能大于真正的短路電流，針對此種情況提出長期尺度估計方法，利用SOC差的累計來抑制瞬時誤差的影響。并通過窗口移動計算不同時間的短路電阻。

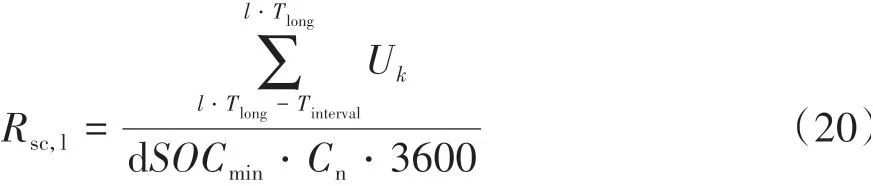
式中：l為計算次數；Tlong為設置的窗口移動步長；Tinterval為 窗 口 長 度，即 當 時 間k=l?Tlong（l=1，2，3，…）時，計算一次短路電阻。

2.2 電池端電壓變化規律及診斷策略

對電池1階RC模型的極化環節進行泰勒多項式展開，并忽略高于2階的項，可得

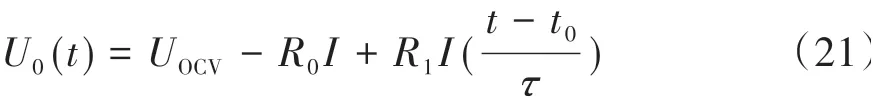
當負載電流變化為ΔI時，端電壓變化為

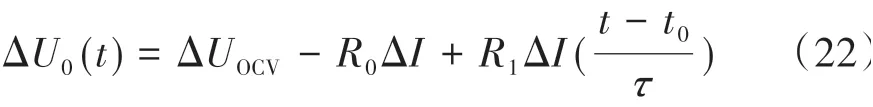
式中ΔUOCV因瞬間變化很小，可忽略不計，同時變化瞬間t接近于t0，式（22）可寫為

短路時R0將變為正常時的Rsc/(R′+Rsc)倍，所以瞬間電壓降可表示為

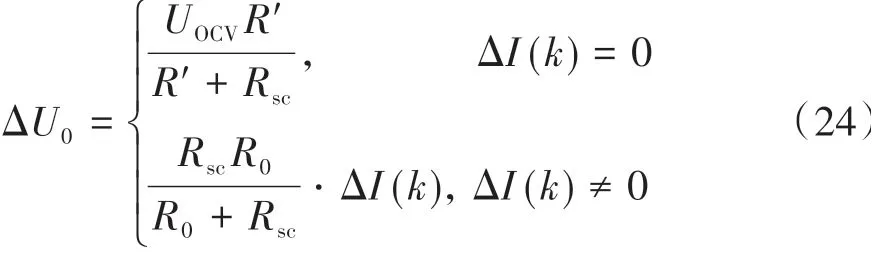
當電池長期靜置時R′=R0。則短路電阻可初步估計為

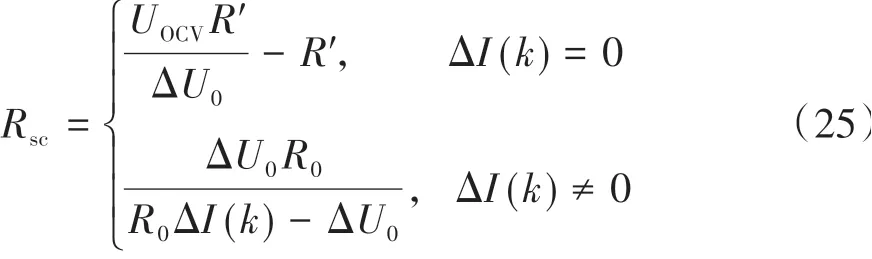
但只利用瞬時電壓降無法將真正短路與傳感器受干擾而波動和短路的熔斷等現象區分，且電池管理系統采樣率較低，電壓降受快速脫嵌反應［14］影響，使計算結果可能存在一定誤差。所以利用瞬時電壓降的短路電阻計算可作為初步預警，若后續時刻的短路電阻估計值能收斂到該值附近，則可說明短路的發生。

綜上，對于不同程度的短路，其電壓信號的特征與短路電阻大小有關。為減小傳感器噪聲及模型估計誤差影響，短路電流估計方法應有所差異，即根據在短路瞬間是否有明顯壓降將估計方法分為短時尺度和長時尺度，并利用瞬時壓降對短時尺度短路電流進行初步估計。圖2為整體估計流程。

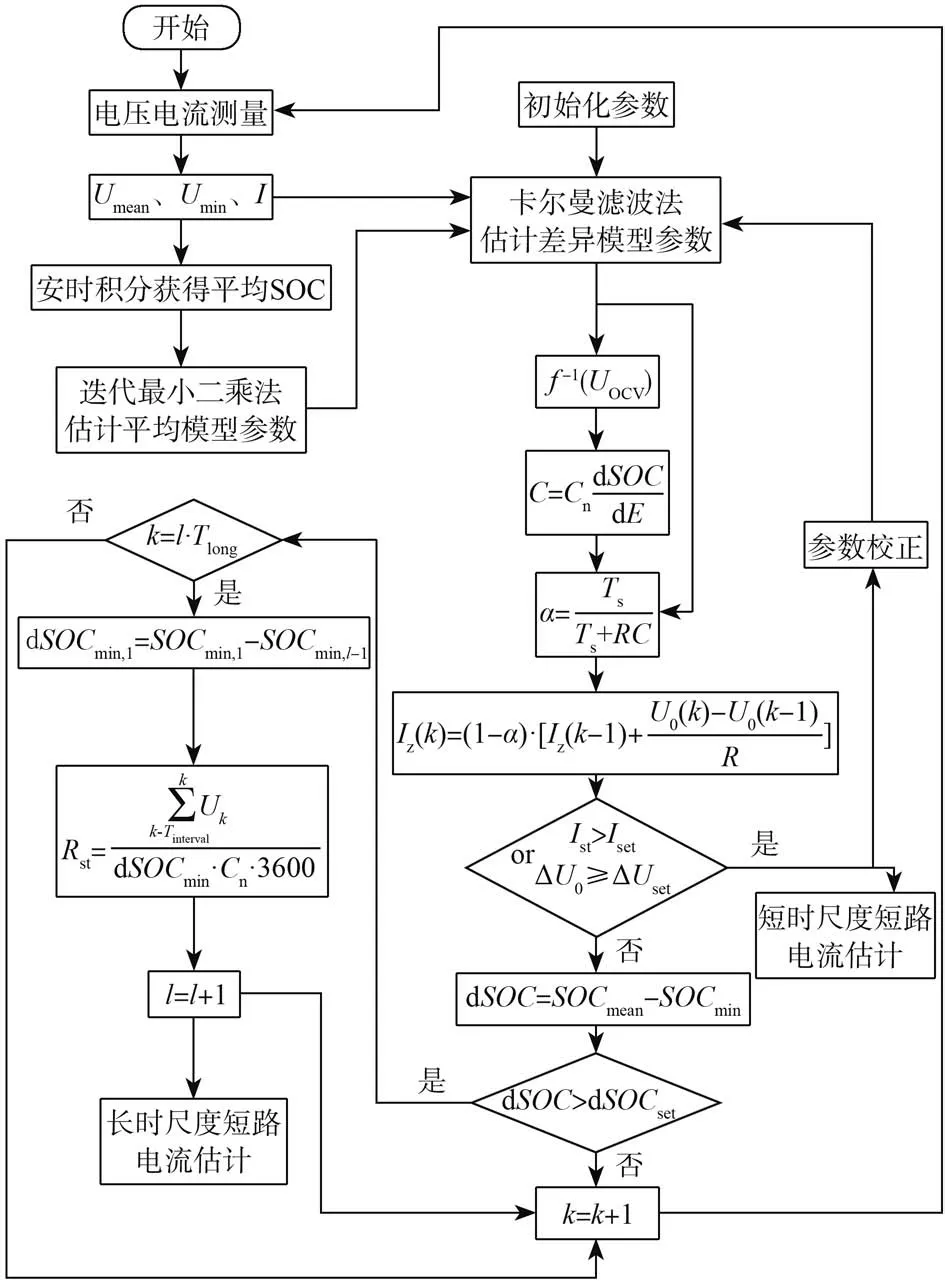
圖2 算法流程

3 實驗方法驗證

通過實驗對本文所提出的短路電流估計方法的有效性進行驗證。圖3為實驗測試系統，實驗測試設備采用Neware CT4000電池測試儀和WHTM?225恒溫箱，電池組由6節10 A·h NCM鋰離子電池串聯。通過上位機設置電池充放電工況，實時采集電池數據，采樣頻率為1 Hz。參照文獻［1］中的方法通過外接不同短路電阻模擬電池內短路各種工況。由于電阻的阻值會隨溫度變化，無法獲得精確值，故將短路電流作為判斷依據，同時將安時積分法獲得的參考開路電壓和SOC與利用算法得到的估計值做比較。實驗工況設定為DST動態工況，短路電阻分別設定為0.2、0.5、1、5和10 Ω，將造成不同程度瞬時壓降。電阻于1 800 s并聯于電池兩端，模擬電池短路。

圖3 實驗測試系統

3.1 短時尺度短路電流估計

當短路電阻值分別為0.2、0.5和1 Ω時，短路電池端電壓和正常電池端電壓平均值的對比如圖4所示。可以看出，在1 800 s短路發生瞬間，短路電池電壓明顯下降，隨后差距逐漸變大。利用瞬時壓降和式（25）對短路電阻進行計算，分別得到0.21、0.47和0.88 Ω，可以初步對短路進行估計。

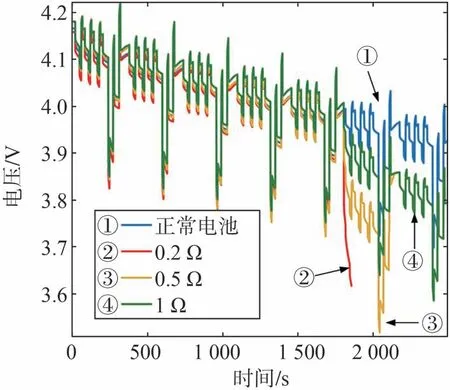
圖4 短路電池端電壓變化

以0.5 Ω短路電阻為例，短路發生時RC參數的變化如圖5所示。在初始時刻，由于初始值未知，存在短時的波動，但很快收斂到穩定值。在未發生短路時，正常電池和短路電池參數由于電池的不一致，參數存在一定差異，但差異保持在一定范圍內。當發生短路時，電池參數隨端電壓快速發生變化，在變化過程中，歐姆電阻R0變化較小，而極化電阻R1明顯增大，主要由于大電流導致鋰離子快速消耗，降低了電解液電導率。極化電容C1減小，主要是由于雙電層的電荷釋放導致。擴散時間常數R1C1會變大，說明極化電壓恢復緩慢，鋰離子擴散受到限制。上述參數的變化規律可以作為判斷短路發生時的輔助特征。

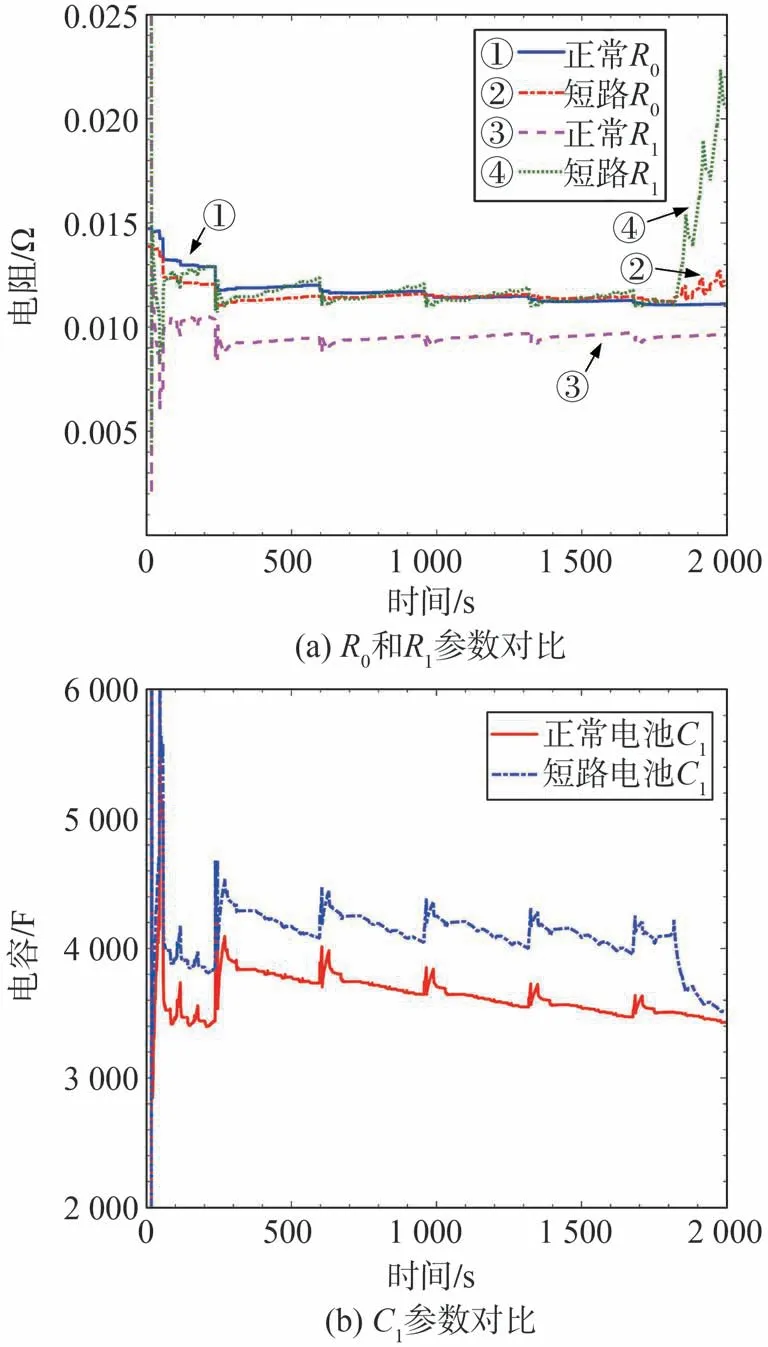
圖5 電阻短路發生時參數的變化

圖6 （a）為估計的SOC與安時法獲得的參考值對比。可以看出兩者的誤差較小。圖6（b）為OCV的估計結果，其與SOC具有相似的趨勢，主要是由于SOC變化幅度較小，而SOC-OCV局部可看作線性關系。兩者的準確度為參數C的計算提供基礎。

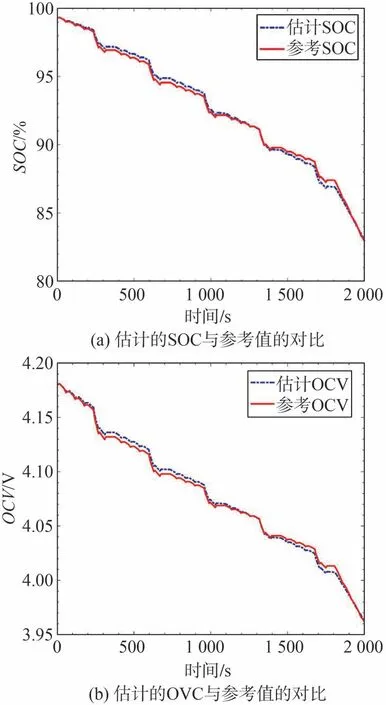
圖6 SOC和OCV估計值（0.5 Ω短路電阻）

圖7 為連接不同短路電阻時估計的短路電流與測量值（實線）的對比。由于參數的估計誤差以及模型的高頻響應差等原因，導致估計值與測量值存在一定偏差，但誤差始終在一定范圍內，可以有效地收斂到測量值。

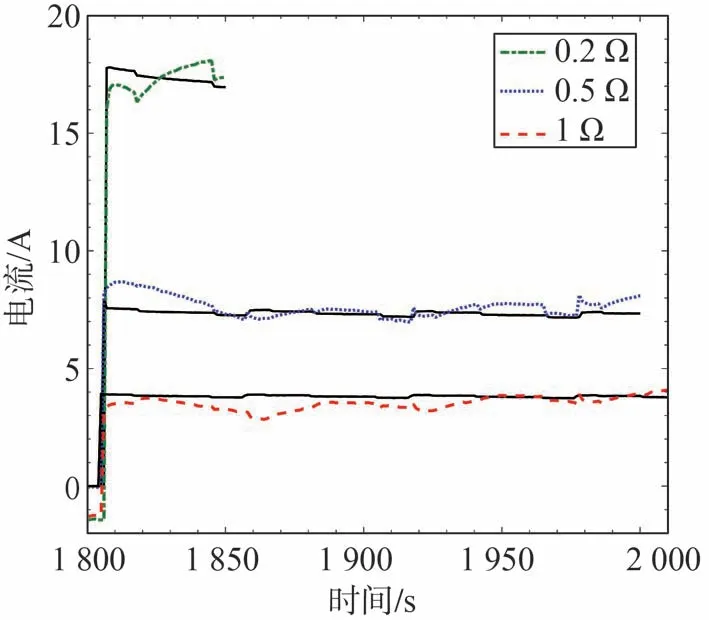
圖7 連接不同短路阻值時短路電流估計值與測量值對比

圖8 為估計的短路電阻與參考值的對比。可以看出，估計值可以快速收斂到參考值。當短路電阻為1 Ω時，電阻估計值有較大的波動幅值，主要是由于此時SOC異常消耗較少，電壓異常變化幅值較小，電流計算值受電壓測量精度影響較大，且易受累計誤差的影響。但較大短路電阻瞬時危害較小，可以利用較長時間的累計SOC差來抑制瞬時誤差的影響，故提出長時尺度短路電流估計以提高較輕微短路時的估計精度。

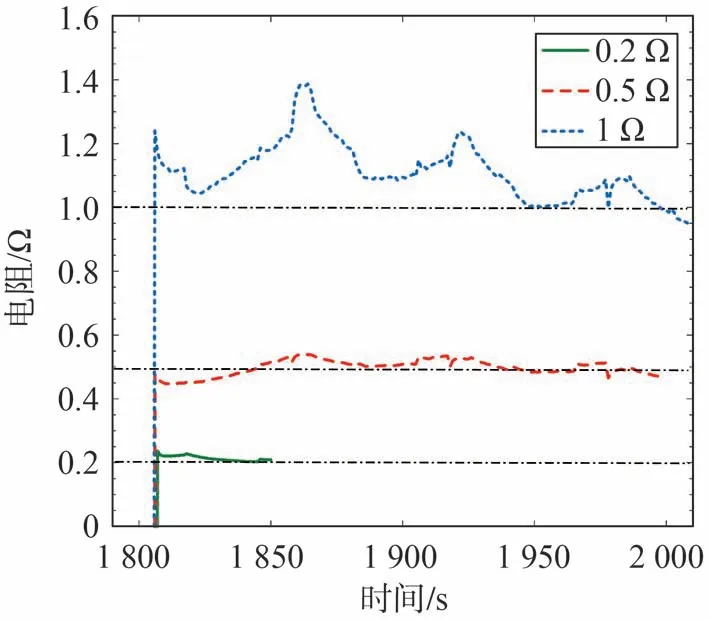
圖8 連接不同短路阻值時電阻估計值與參考值對比

3.2 長時尺度短路電流估計

長時尺度短路電流估計主要依據短路造成的SOC異常下降，當短路電阻值分別為5和10 Ω時，短路電池與正常電池端電壓對比如圖9所示。電壓在短路瞬間沒有明顯變化，而是逐漸偏離正常電池電壓。

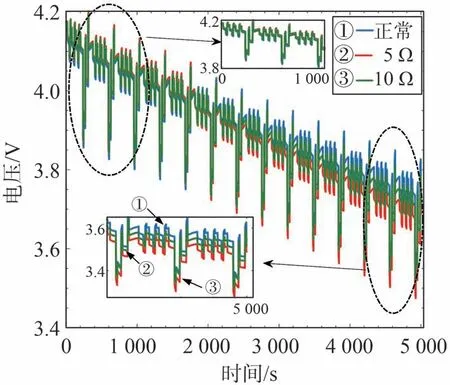
圖9 端電壓與正常電壓對比

圖10 為電池模型辨識獲得的參數隨時間的變化。從圖中可以看出，當短路發生后R0和R1略微增大，C1基本保持不變，與正常電池相比差異變化較小。由于5 Ω電阻造成的短路電流倍率小于0.08C，引起的額外極化很小，使電池參數更多表現為隨SOC和溫度變化，不會對電池造成明顯的擴散限制。

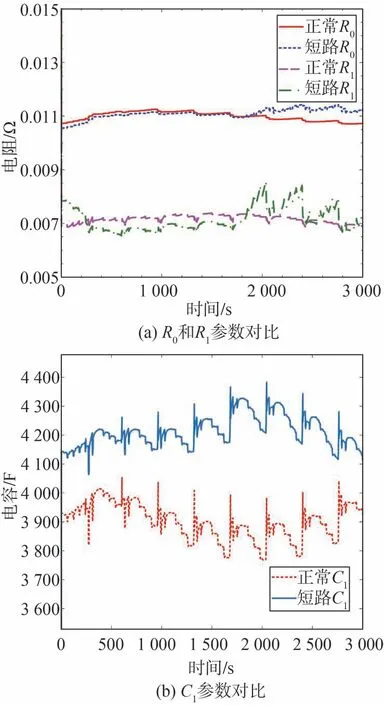
圖10 電阻短路發生時RC參數的變化

圖11 為短路電阻是5 Ω時估計的OCV和SOC與參考值對比。可以看出，誤差小于1%，估計精度較高。短路造成的等效參數與實際值差距較小，即Rsc/(R′+Rsc)≈1，受平均-差異模型誤差影響較小。

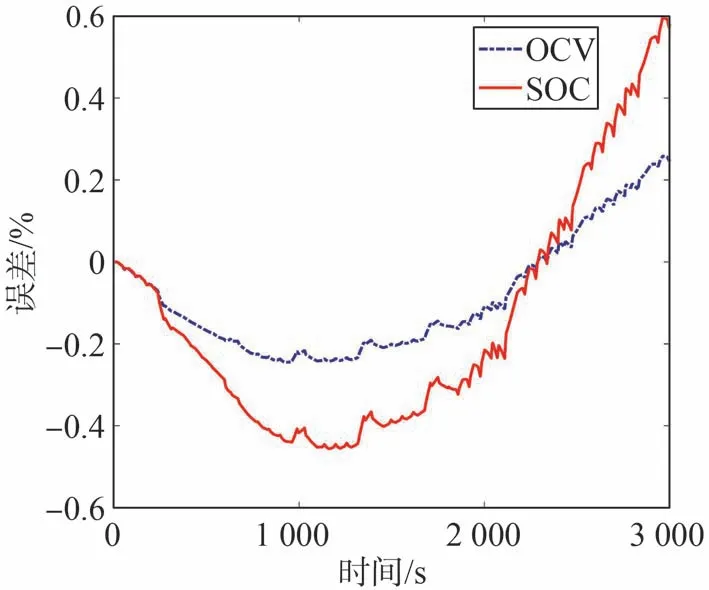
圖11 估計的OCV和SOC的誤差百分比

由式（20）可知估計結果和窗口長度有關，改變窗口長度影響波動幅值。圖12（a）為短路電阻是5 Ω時不同計算窗口長度Tinterval下的短路電阻估計結果。由于短路發生時刻沒有明顯短路特征，使窗口起始部分包含未短路時刻的數據，造成初始時刻有較大偏差。但不同的Tinterval最終均可以收斂到參考值，且Tinterval越小，收斂速度越快，但受瞬時SOC估計誤差的影響，短路電阻的估計值波動越大。當短路電阻為10 Ω時，計算結果如圖12（b）所示，相比于5 Ω，在同一窗口長度下的波動幅值更大，主要是由于10 Ω短路造成的SOC消耗少，計算結果受瞬時波動的影響更大。為均衡波動和收斂速度，可選擇Tinterval=500 s作為計算窗口長度。

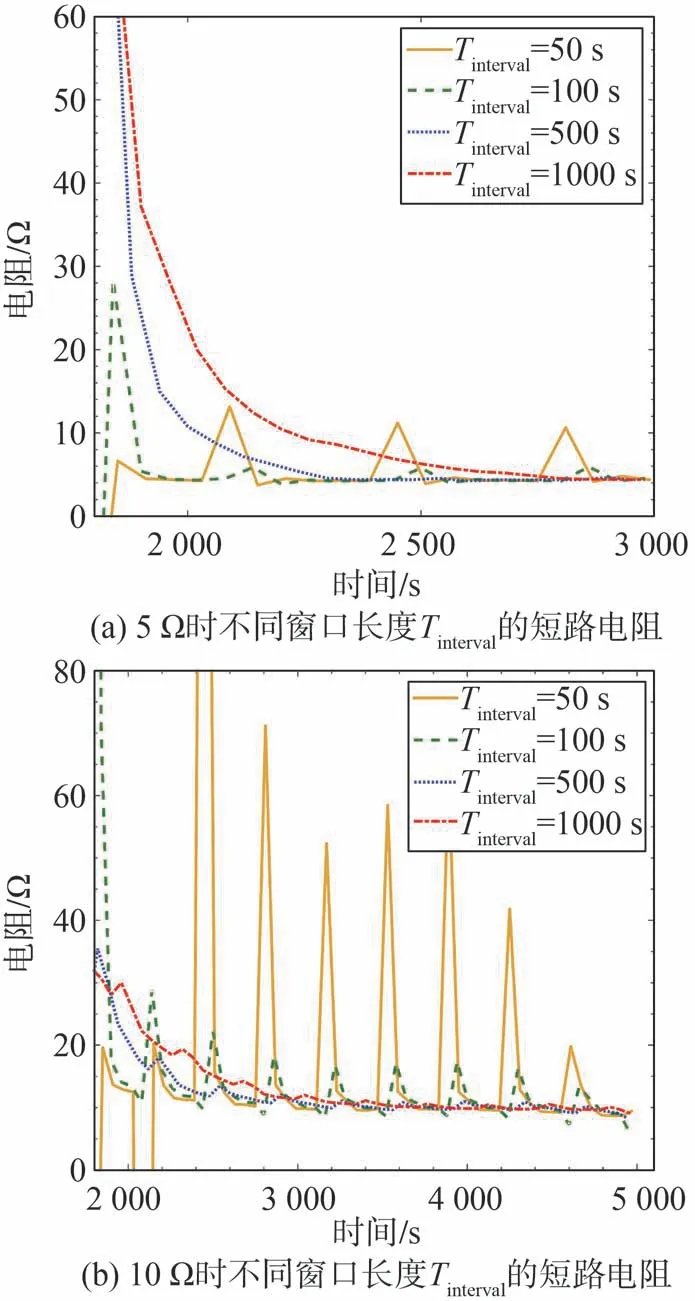
圖12 窗口長度影響及電阻估計值

4 結論

提出了一種基于電池平均-差異模型的多尺度短路電流估計方法。分析了模型精確度以及參數辨識與校正方法，推導了基于模型參數和端電壓的短路電流估計方法，實現短路電流的快速準確診斷，得出結論如下。

（1）短路電池可以使用1階RC模型進行等效，但在短路電阻較小時等效參數與實際參數差異較大，須進行參數校正，以提高模型精確度。

（2）當短路瞬間有明顯壓降時，利用RC參數和瞬時壓降可以對短路電阻初步計算并預警。

（3）模型的RC參數變化與短路的嚴重程度相關，當短路較為嚴重時，極化電阻和擴散時間常數明顯變大。而輕微短路時，參數更多隨SOC和溫度緩慢變化。

（4）對于較為嚴重的短路，利用短時尺度估計方法可以在短路發生的下一個采樣時刻實現短路電流的計算。臨界短路電阻1 Ω時短路電流的估計誤差小于20%，且電阻越小，誤差比例越小，從而實現短路的快速診斷。而較大電阻的微短路計算利用SOC的異常消耗，采用長時尺度估計方法可以提高其精確度。其收斂速度和窗口長度有關，選擇Tinterval=500 s可以兼顧波動性和快速性。5和10 Ω時的誤差比例均小于5%，實現了長時尺度的準確估計。