卷揚機卷筒工藝誤差及其影響分析

□ 蒲鵬杰 □ 王海珍

蘭州通用機器制造有限公司 蘭州 730050

1 分析背景

舞臺用卷揚機卷筒結構有整體焊接式和組裝式兩種,整體焊接式卷筒結構如圖1所示。

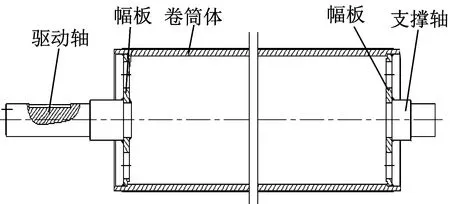
▲圖1 整體焊接式卷筒結構

整體焊接式卷筒可以看作是細長軸與突變截面組合的特殊結構,此類結構卷筒體的繩槽車削采用成形刀具,成形刀具吃刀受力面大,會導致刀具切削徑向力大,刀桿變形大,容易產生振動,增大了加工難度。另一方面,由于突變截面的特殊結構,使卷筒軸上的鍵槽加工也難度增大。由此,整體焊接式卷筒不易保證加工精度。

為了克服上述加工困難的情況,一些企業在生產中采用組裝式卷筒,通過分體加工來減小加工難度。加工時,分別保證組裝部件的精度,通過組裝來保證組裝式卷筒的整體精度。當然,由于組裝結構的工藝特點,會使裝配累積誤差增大。筆者對組裝式卷筒的工藝誤差和影響進行分析。

2 組裝式卷筒結構特點

組裝式卷筒的結構如圖2所示,由驅動軸、平鍵、軸套、幅板、支撐軸組成。

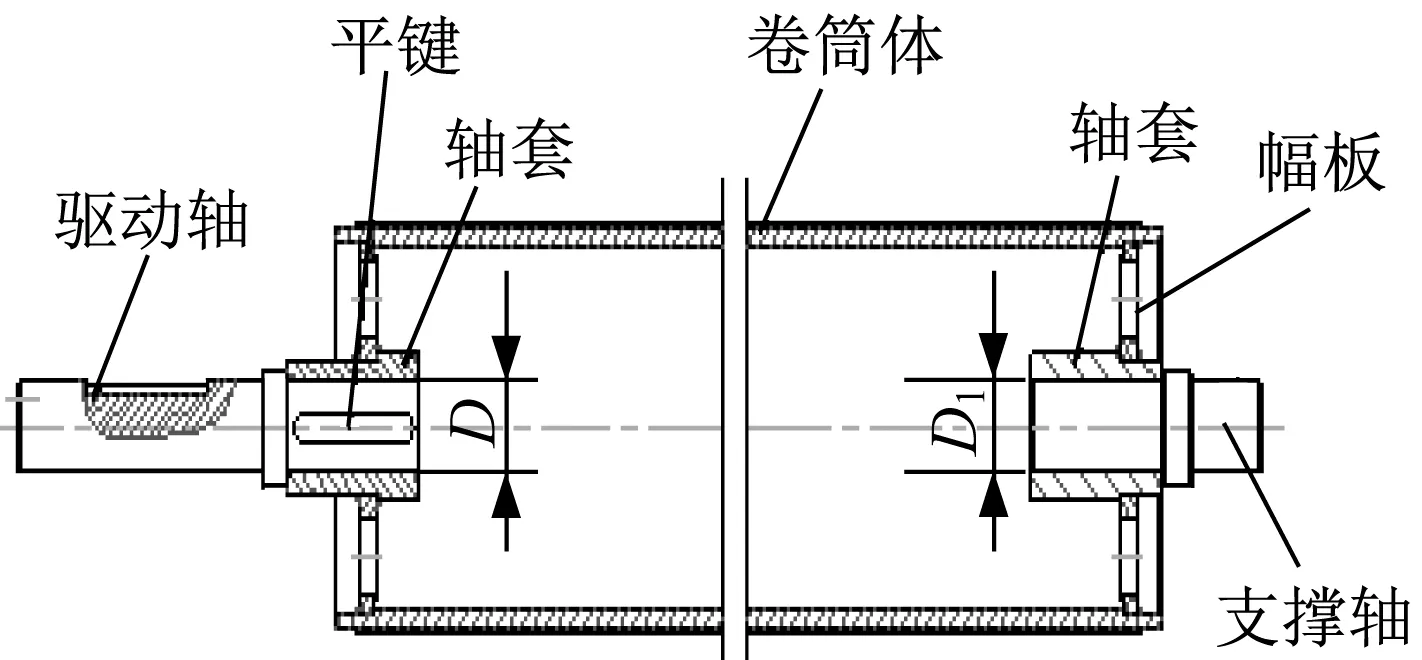
▲圖2 組裝式卷筒結構

由圖2可知,組裝式卷筒結構的組裝精度取決于卷筒體的兩幅板與軸套孔徑D、D1的垂直度,軸套孔徑D與D1的同軸度,裝配后驅動軸和支撐軸的同軸度。隨著卷筒體長度增大,這些位置公差的精度很難保證,生產加工中的累積誤差也會隨之增大。

3 誤差分析

組裝式卷筒加工中的難點是要保證滾筒體兩軸套孔的同軸度、兩軸套孔與螺旋槽節圓的同軸度、兩軸套孔鍵槽的位置精度。

裝配產生的同軸度誤差Ha及裝配后產生的累積誤差如圖3所示。卷揚機的結構如圖4所示。由圖3及圖4可以看出,裝配工藝以基座和墻板為基準,若兩軸套同軸度誤差大,即使使用立式帶座調心軸承也裝配不上。按照卷揚機現行裝配工藝,以驅動軸端為基準進行裝配,若兩軸套同軸度誤差大,則可以改動驅動軸端安裝位置來完成裝配。立式帶座調心軸承并不能抵消兩軸套同軸度誤差,只是通過自身結構使卷筒體完成旋轉。無論采用何種裝配形式、何種類型軸承,加工及裝配產生的誤差并不能被消除,卷揚機工作時的轉動慣量、臨界轉速將會受到影響。

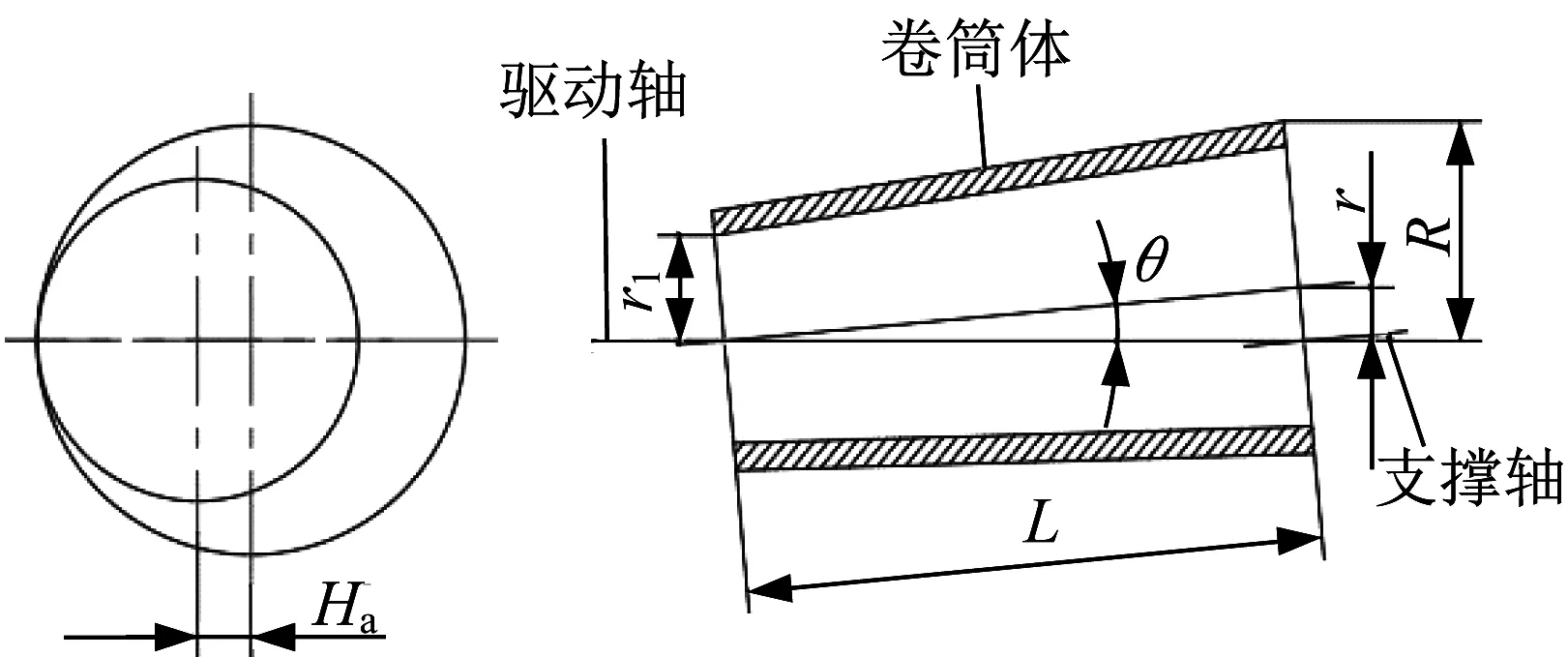
▲圖3 誤差示意圖

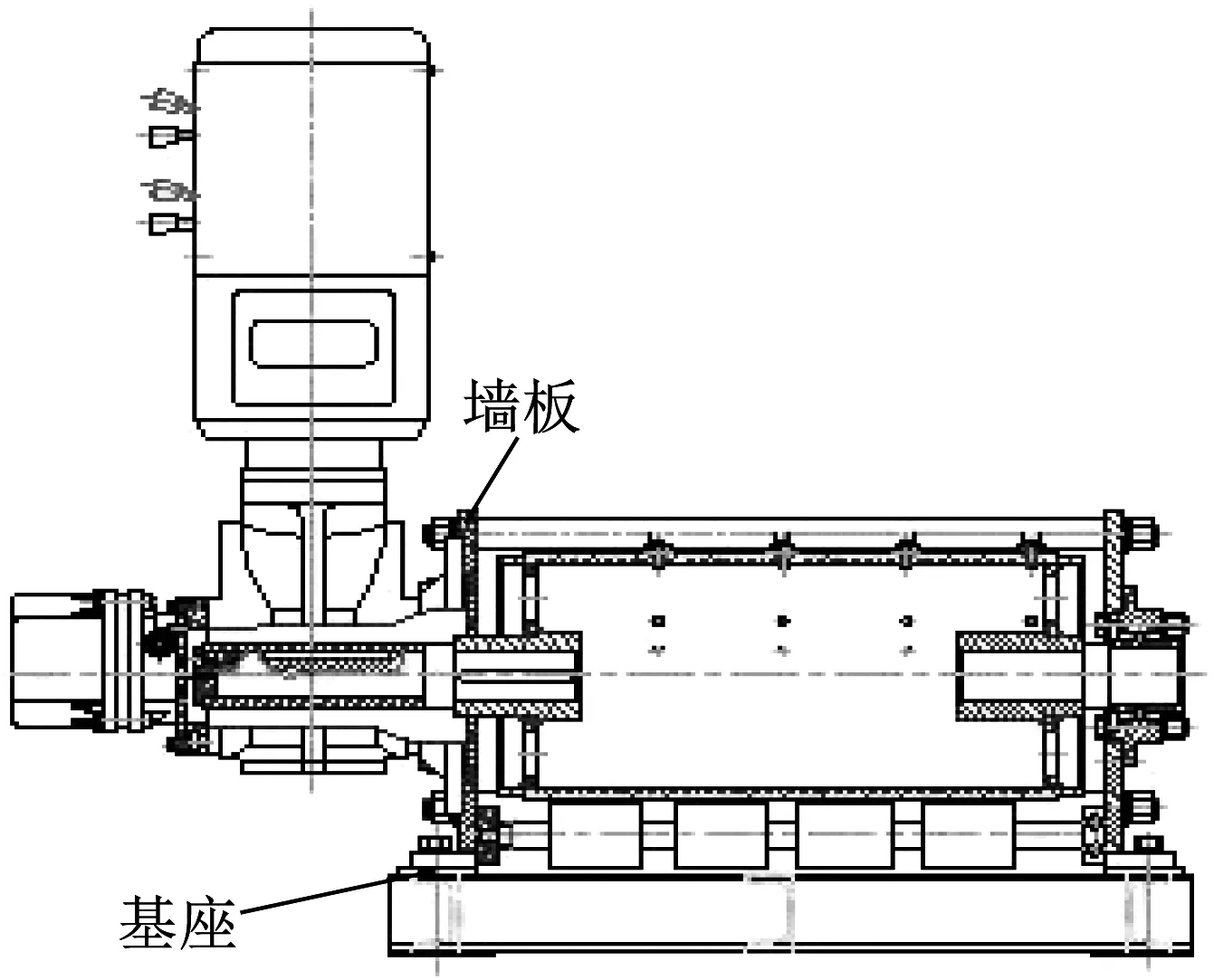
▲圖4 卷揚機結構

4 轉動慣量分析

根據轉軸線偏移原理,對偏心距e積分,求出偏心距變化對轉動慣量的影響。

轉軸線與卷筒體質心有偏心距時,轉動慣量I為:

I=Icofm+me2

(1)

式中:Icofm為卷筒體質心與轉軸線重合時的轉動慣量;m為卷筒體質量。

(2)

式中:R為卷筒體外半徑;r1為卷筒體內半徑。

對偏心距e積分,轉動慣量增量J為:

(3)

θ=β+arctan(Ha/L)

(4)

β=α3+α4

(5)

L=r/sinθ

我一點也不是恩將仇報，我把三妮交給了楊家之后。楊家強迫她嫁到西山窩。我找了幾次，也沒找到她。后來三妮又跑來跟了我。那時，挖河打堰用工多，一到冬天，我經常被派出去挖河。四細狗這狗日的，趁我不在家，就把三妮給勾上了。

(6)

式中:θ為累積誤差產生的轉軸線與卷筒體質心軸線的角度;β為找正誤差、定位誤差、車削誤差產生的累積誤差軸線與卷筒體自身誤差的角度;L為卷筒體長度;r為裝配后所有累積誤差產生的同軸度誤差最大值;α3、α4分別為加工時的找正、重復定位誤差。

求式(3)與式(2)的比值x:

(7)

x=Asin3θ

(8)

式(8)表明非偏心轉動慣量與偏心時轉動慣量的增量關系。

由式(8)可以看出,同軸度誤差增大而產生的轉動慣量非常小,A與卷筒體長度、卷筒體內外徑相關,在卷筒體足夠長,且半徑較大時,應當注意轉動慣量的影響。

5 臨界速度分析

力學模型如圖5所示。根據能量守恒定律,求卷筒體的撓度。對卷筒體的撓度計算建模,將卷筒體視為單圓盤簡支模型。卷筒體吊點往往有很多個,根據線性原則,可將卷筒體分為多段計算,吊點載荷相等。

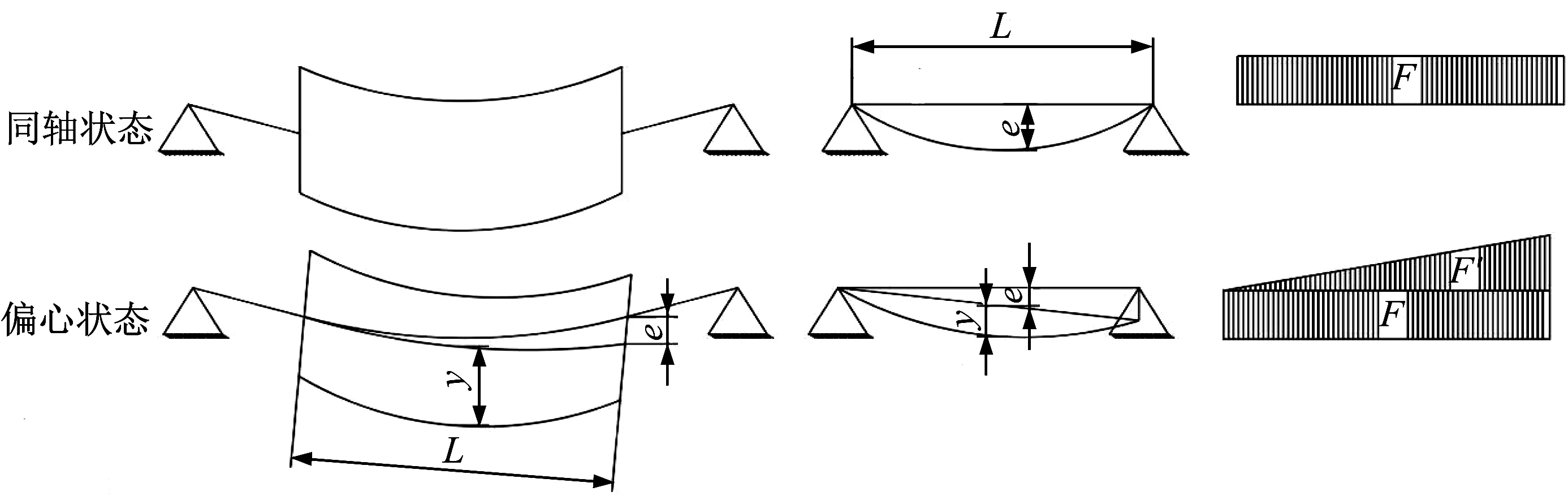
▲圖5 力學模型

分別列出滾筒體與兩軸線同軸和偏心狀態時的能量守恒公式,根據能量守恒公式推導分析所需要的變量。同軸狀態時有:

(9)

偏心狀態時有:

(10)

式中:F為載荷;y為變形量;F′為離心力;ω1為同軸狀態的臨界轉速;ω2為偏心狀態的臨界轉速。

由式(9)、式(10)可知,偏心狀態時,在離心力F′的影響下,撓度具有增大的趨勢。在計算撓度時,忽略離心力的影響,可以認為同軸狀態和偏心狀態下撓度相等,即彎曲變形相等。于是,同軸狀態時有:

(11)

偏心狀態時有:

(12)

式中:yi為每處吊點的變形量;i為吊點數。

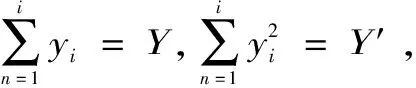
(13)

根據式(11)、式(13),得:

(14)

由式(14)可以看出,兩種狀態下的臨界速度比值與最大偏心距有關,影響的重要性還要和自身變形量作比較,若偏心距誤差較大,必須驗算臨界速度。

6 結束語

根據以上計算分析可知,組裝式卷筒在生產裝配中的累積誤差會對卷揚機運行中的轉動慣量、臨界速度產生一定影響。當累積誤差較大時,需要進行驗算,以規避累積誤差對卷揚機運行的影響。