基于領航跟隨的多機器人編隊控制方法

高繼勛，黃全振，趙媛媛

（1.河南工程學院計算機學院，河南 鄭州 451191; 2.河南工程學院電氣信息學院，河南 鄭州 451191;3.鄭州工程技術學院，河南 鄭州450044）

0 引 言

隨著人工智能時代的到來，多機器人的控制已逐漸成為研究熱點[1-6]，其應用場景包括但不限于農業、軍事、航空等領域。在多機器人編隊的協同控制過程中，通常所期望隊形是可變的，以便于應對單個機器人無法完成的復雜任務。在極坐標下，利用線性反饋的方法建立“距離-角度”控制器模型，完成對多機器人編隊控制[7]。由于奇異點存在，該控制器存在一定問題。可通過將極坐標投影到笛卡爾坐標系下，重新建立控制模型解決奇異點問題[8-9]。鐘宜生等[10]提出，將多機器人可變編隊問題描述為“不變的隊形在可變的坐標系中運動”的編隊控制問題。在上述基礎上，李清東[11]提出用多個不變隊形互相切換，以完成編隊控制。劉磊[12]采用以差速輪式機器人為研究對象，通過仿真驗證該控制方法的可行性。

目前對于解決多機器人一般性編隊控制問題，公開文獻中尚未見到成熟方案。現階段主要有人工勢場法[13]、基于行為法[14]、虛擬結構法[15]和領航-跟隨法[16]。上述方法各有其優缺點，相比較而言，領航-跟隨法的控制更簡單，只需調整跟隨者與領航者的運動參數即可完成跟蹤控制，具有較好的穩定性和靈活性[17-20]。

根據上述情況，本文提出了一種新穎的機器人編隊控制方法，該方法基于領航-跟隨法，引入“虛擬領航機器人”，將其他機器人作為跟隨者，建立控制模型，從而將編隊問題轉化為跟蹤控制問題。根據提出的控制算法，本文設計了跟隨誤差控制器，分析跟隨誤差及其收斂性。通過仿真與實驗結果分析，驗證本文提出的改進型領航-跟隨控制方法在一致性控制中的有效性與穩定性。

1 問題描述和模型構建

1.1 問題描述

基于領航-跟隨法，可將編隊問題轉化為跟隨機器人對虛擬領航機器人的軌跡跟蹤，該方法只需獲得虛擬領航者的運動參數和位姿即可實現跟蹤控制，一定程度上減少相互之間信息冗余及計算量。通過上述方法，建立虛擬領航機器人與跟隨機器人運動模型，如圖1所示。

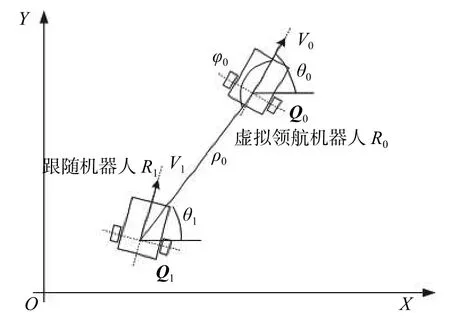
圖1 領航-跟隨結構示意圖

圖中，跟隨機器人R1與虛擬領航機器人R0的距離是ρ0，二者中心線連線與虛擬領航機器人R0軸心線的夾角是φ0。通過虛擬領航者的引入，將編隊控制轉化為跟隨移動機器人R1對虛擬領航機器人R0的軌跡跟蹤，即跟隨機器人R1在一定時間內跟隨虛擬領航機器人R0運動就可組成相應的編隊。

1.2 模型構建

非完整移動機器人的運動學模型[15]如下式：

由圖1可知，當跟隨機器人R1與虛擬領航機器人R0之間的位姿（位置和姿態）誤差趨近于零，即：

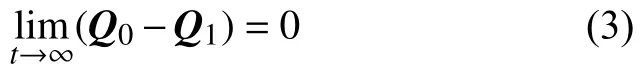
假設在t時刻，虛擬領航機器人與期望軌跡運動示意圖如圖2所示。

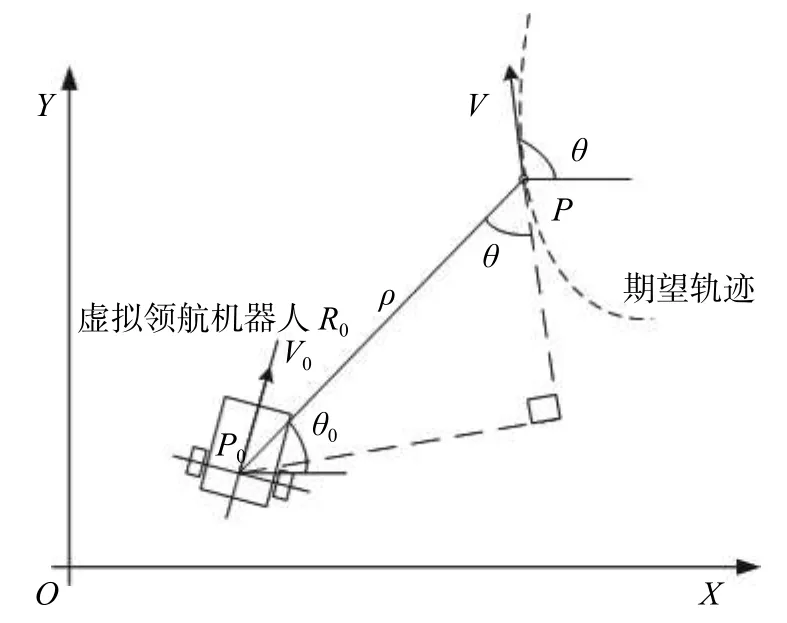
圖2 跟蹤位置示意圖

其中，V為期望軌跡上P點的運動方向，與X軸正方向夾角為θ。P0P為虛擬領航機器人與期望軌跡上P點的連線。P點狀態表示為（X,Y,θ）。

虛擬領航機器人與期望軌跡誤差參數表示為：

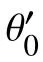
通過對參數λ的調整，可完成跟隨機器人相對于期望軌跡的控制。

虛擬領航機器人運動學模型可表示為：

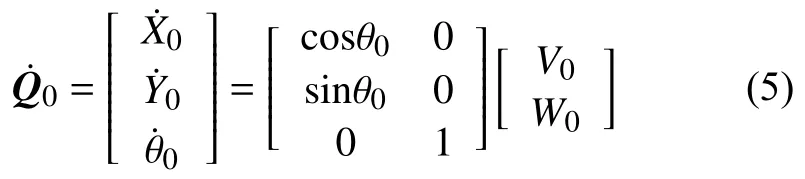
跟隨機器人參考軌跡模型為：

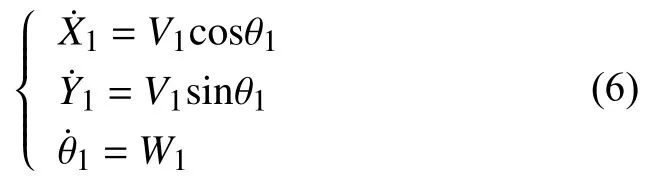
根據期望軌跡P點狀態及公式（4）可得到虛擬領航機器人位姿，其數學表達式如下：

2 控制器設計

跟隨機器人R1與虛擬領航機器人R0位姿誤差為ei，則ei可表示為：

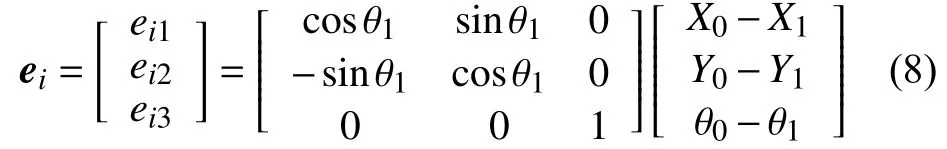
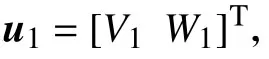
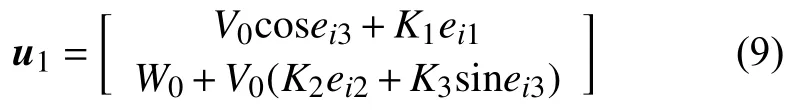
其中，K1，K2，K3為正數。

定義Lyapunov函數VL為：

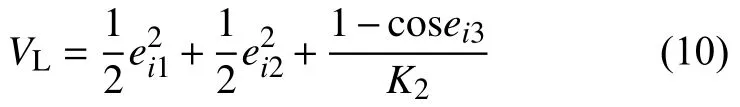
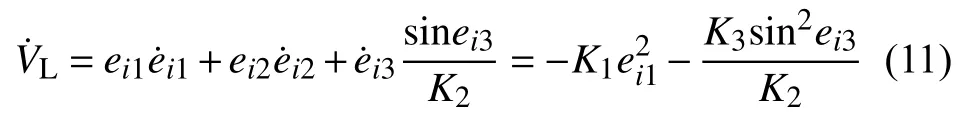
以上構建了基于領航跟隨運動控制方法的控制器，并且證明了該控制器的穩定性。下面對該方法進行仿真與實驗研究。

3 仿真分析與實驗驗證

為驗證系統及控制算法的正確性和有效性，利用仿真軟件和硬件平臺構建模擬/物理實驗系統進行驗證。仿真采取與期望軌跡重合（追蹤）、與期望軌跡保持固定隊形（編隊）兩種情況進行，便于在不同控制場景下對結果分析。

3.1 仿真分析

仿真研究基于Gazebo機器人仿真軟件構建的運動學與控制仿真平臺。仿真固定參數以實際硬件平臺為參考，其固定參數值如表1所示。

表1 仿真基本參數

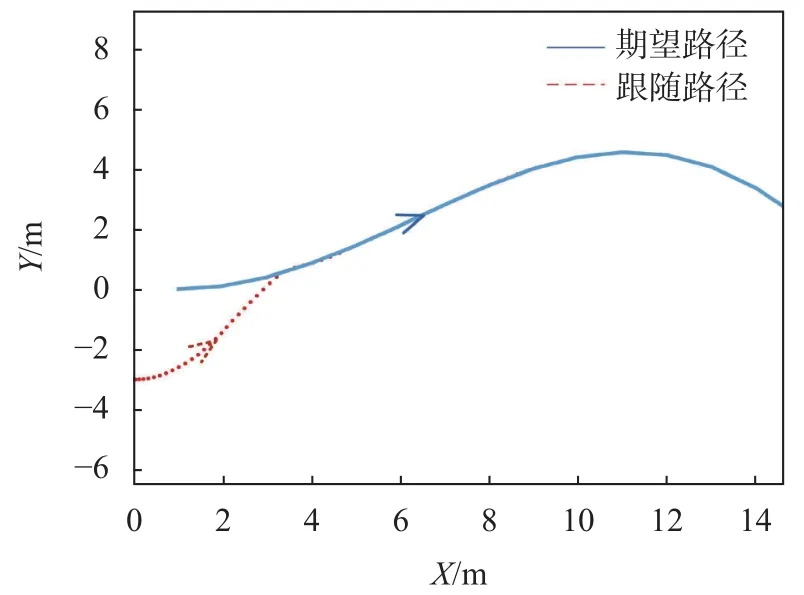
圖3 λ=[0 0]T跟隨機器人仿真運動軌跡

跟隨機器人從任意初始位置開始運動，速度變化曲線如圖4中虛線所示。由圖可以看出，時間T從5 s左右速度開始變化，隨后減小；從20 s左右開始，跟隨機器人速度趨于穩定；30 s時，跟隨機器人速度穩定在 0.8 m/s。

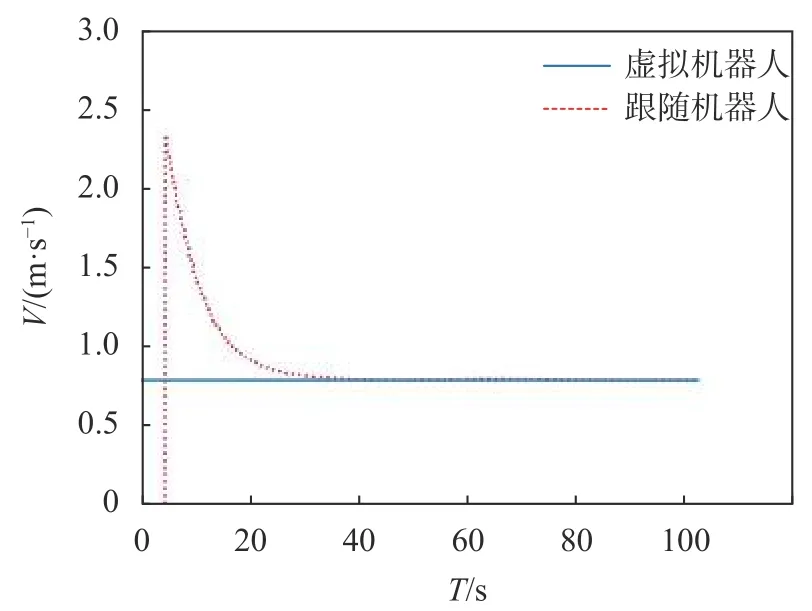
圖4 λ=[0 0]T跟隨機器人仿真速度曲線

設定虛擬領航機器人與期望路徑距離為0.5 m，與速度方向夾角為π/6，即λ=[0.5 π/6]T。假設虛擬領航機器人速度為0.8 m/s，角速度為16 rad/s。即在某時刻，虛擬領航機器人中心線與期望軌跡連線長度為0.5 m，與期望軌跡該點切線方向夾角為π/6。跟隨機器人運動軌跡如圖5所示，其中，X、Y為機器人所處平面坐標，三角形為期望結構，端點為運動軌跡與虛擬機器人期望位置。

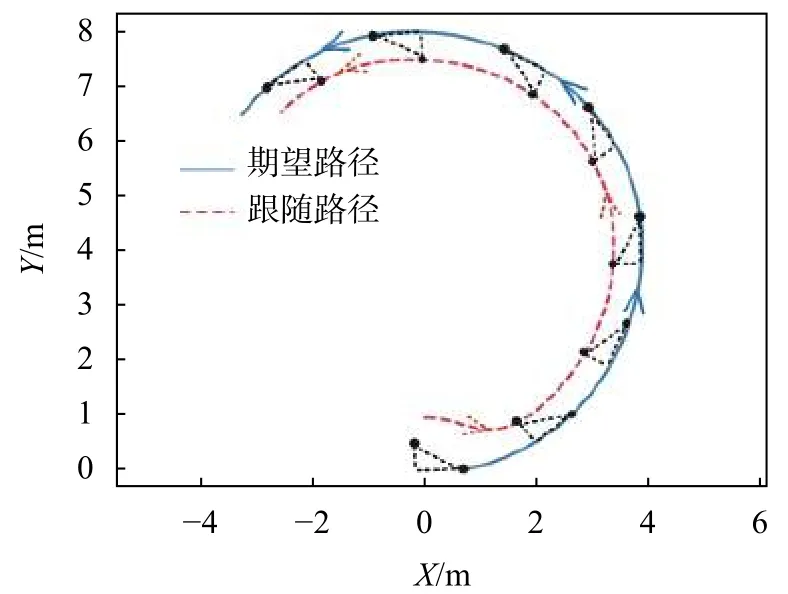
圖5 λ=[0.5 π/6]T跟隨機器人仿真運動軌跡

跟隨機器人速度變化曲線如圖6中虛線所示。當時間T從25 s開始，跟隨機器人速度趨于穩定；40 s時，跟隨機器人速度穩定在0.8 m/s。

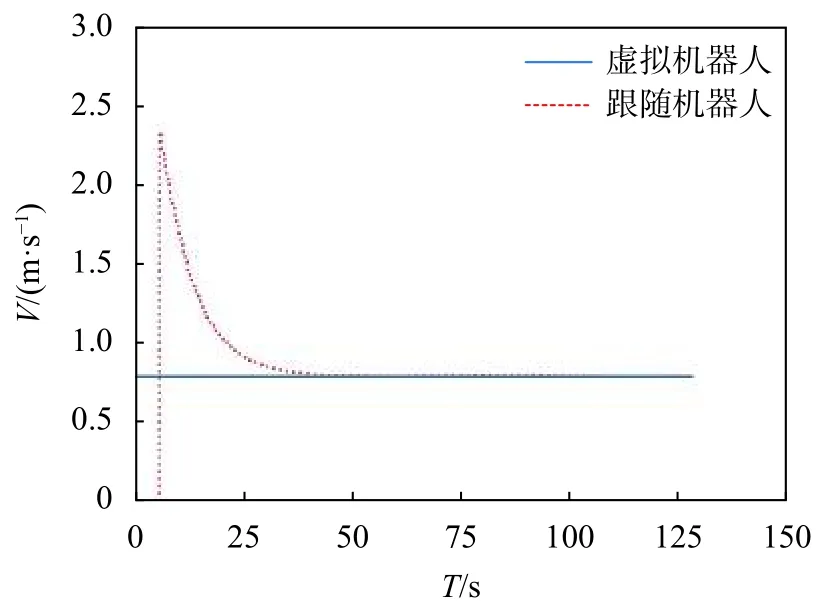
圖6 λ=[0.5 π/6]T跟隨機器人仿真速度曲線

3.2 實驗驗證

為移動機器人控制構建物理實驗系統。該實驗系統的硬件部分主要由雙輪差速驅動底盤、IMU模塊、差分GPS定位模塊（RTK）和主計算機（Raspberry Pi4B）組成。

主計算機主要通過傳感器模塊采集到的數據進行運動狀態計算，并且通過輸出控制指令完成對底盤的運動控制；底盤執行主計算機的控制指令，按照控制指令完成運動；IMU模塊為九軸慣性測量模塊，用于測量機器人的運動狀態，包括加速度和航向角等；差分GPS定位模塊實現機器人的實時定位功能，具體實現為：將差分GPS移動接收端安裝于機器人的底盤上，通過接收衛星與基準站數據進行差分計算，從而提高機器人的定位精度。

實驗平臺示意圖及實物圖如圖7、圖8所示。

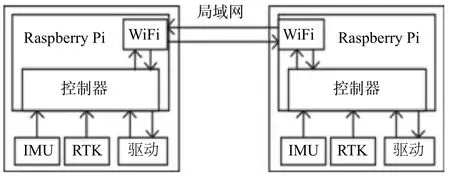
圖7 實驗平臺示意圖

圖8 實驗平臺實物圖

程序流程如圖9所示。首先對跟隨機器人進行狀態初始化；然后根據GPS和IMU回傳數據計算，并于期望位姿做姿態解算；通過結算結果，得到控制輸入參數；最后輸出給控制單元，并實時對跟隨機器人狀態進行監測，判斷其是否達到預期位姿。

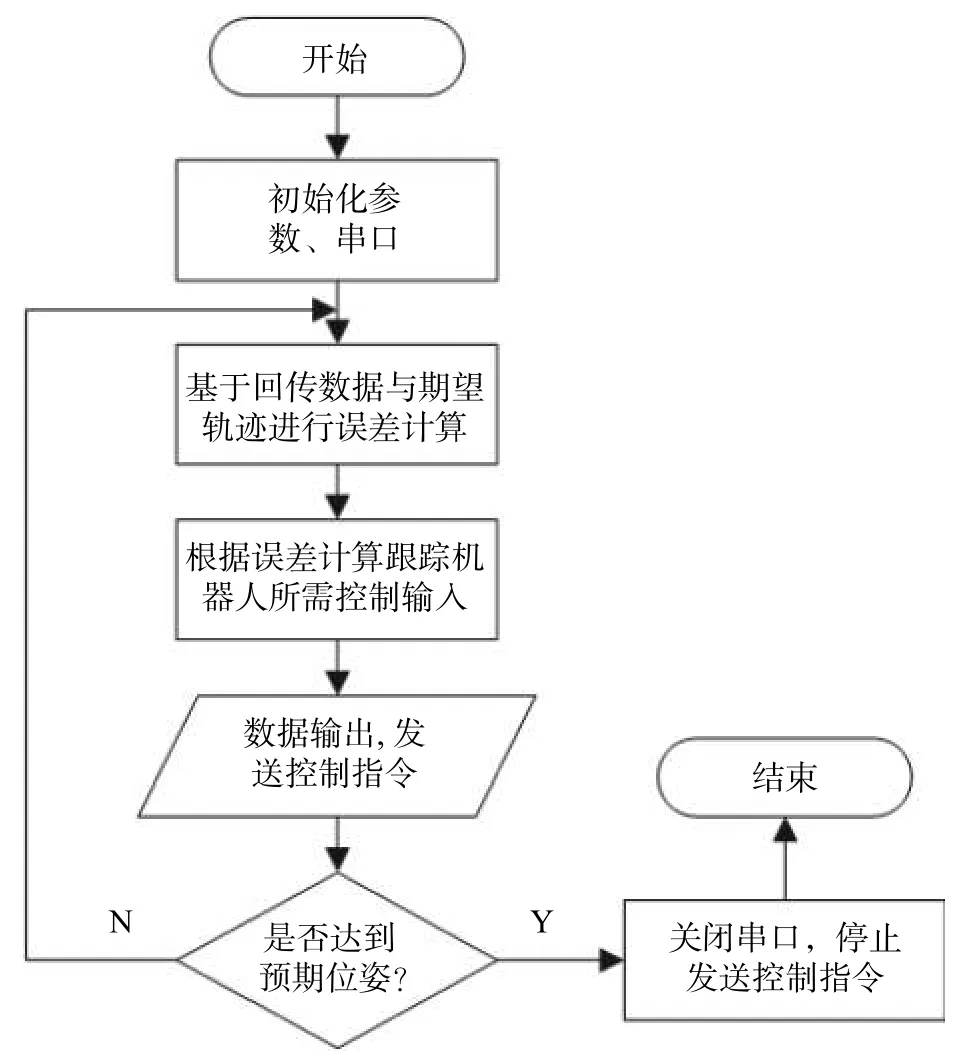
圖9 跟隨機器人控制實驗流程圖

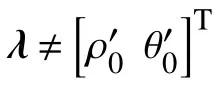
根據預設期望軌跡與虛擬領航機器人的當前位姿誤差，計算跟隨機器人所需控制輸入參數，然后通過串口將運動控制指令發送給運動底盤。如此循環。

設定虛擬領航機器人與期望軌跡重合，即λ=[0 0]T。假設任意初始位置，虛擬領航機器人以速度為0.8 m/s，角速度為0勻速運動。跟隨機器人運動軌跡如圖10所示。其中，X、Y為機器人所處二維平面。

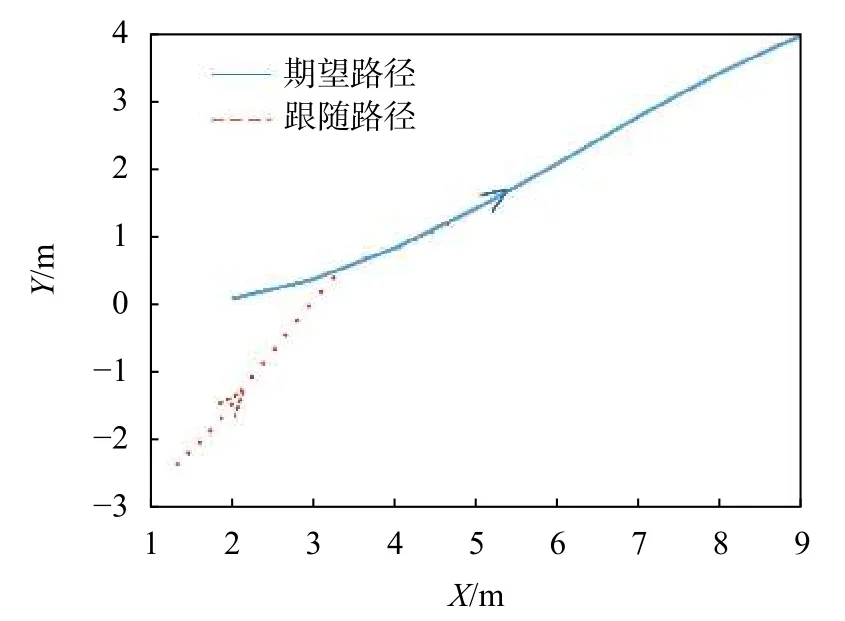
圖10 λ=[0 0]T跟隨機器人實驗運動軌跡

跟隨機器人速度變化曲線如圖11中虛線所示。當時間T從20 s開始，跟隨機器人速度趨于穩定；35 s時，跟隨機器人速度穩定在0.8 m/s。

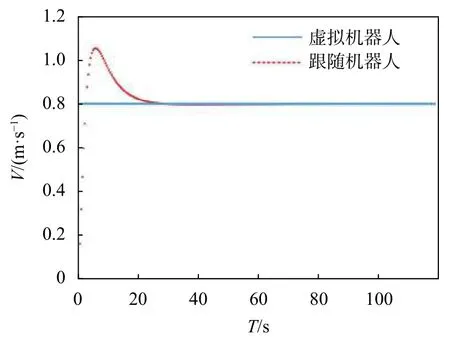
圖11 λ=[0 0]T跟隨機器人實驗速度曲線

設定虛擬領航機器人與期望路徑距離為0.5 m，與速度方向夾角為π/6，即λ=[0.5 π/6]T。假設虛擬領航機器人速度為0.8 m/s，角速度為16 rad/s。即在某時刻，虛擬領航機器人中心線與期望軌跡連線長度為0.5 m，與期望軌跡該點切線方向夾角為π/6。跟隨機器人運動軌跡如圖12所示，其中，X、Y為機器人所處平面坐標，三角形為期望結構，端點為運動軌跡與虛擬機器人期望位置。

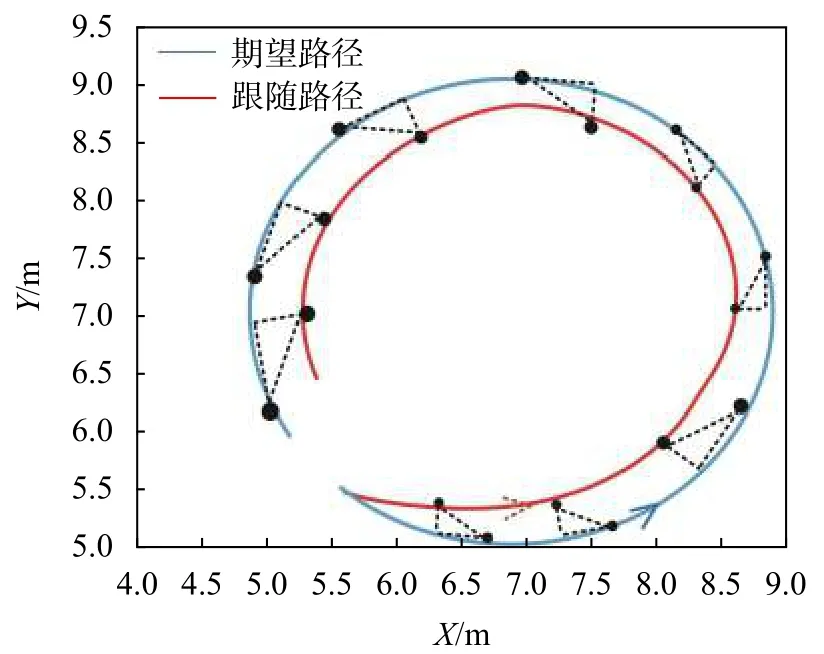
圖12 λ=[0.5 π/6]T跟隨機器人實驗運動軌跡

領航機器人以0.8 m/s速度運動時，跟隨機器人變化曲線如圖13虛線所示。當時間趨于50 s時，跟隨機器人速度穩定在0.8 m/s。

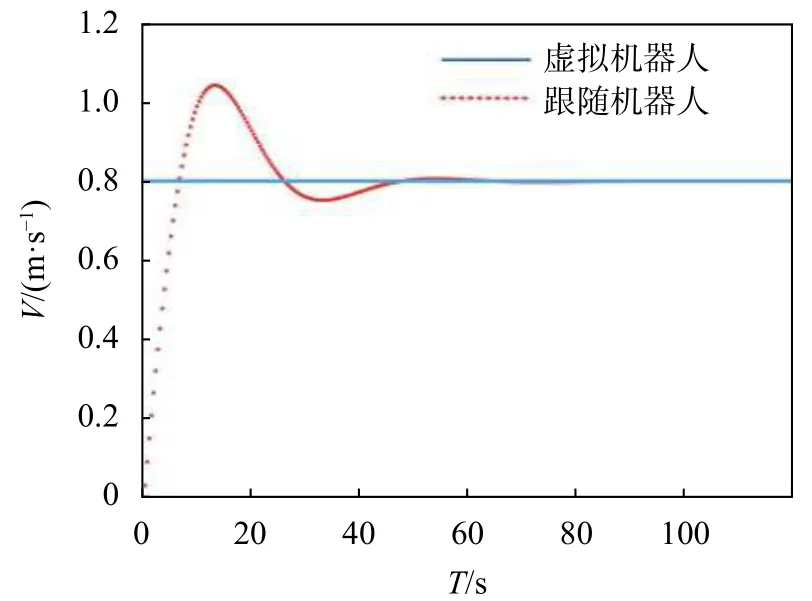
圖13 λ=[0.5 π/6]T跟隨機器人實驗速度曲線

通過對比表2及前文中速度曲線可以看出，跟隨機器人速度、位姿誤差在仿真中收斂較快。并且，跟隨期望軌跡比保持固定距離收斂耗時較少。

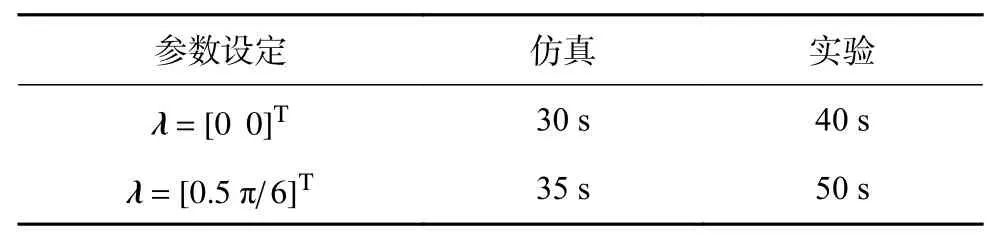
表2 仿真、實驗結果

在一定時間內，跟隨機器人運動速度逐漸收斂至預期，V0?V1在一定時間內趨于穩定。同時，跟隨機器人與虛擬領航機器人位姿誤差也趨近于穩定，系統達到穩定狀態。

4 結束語

本文以輪式差分驅動機器人為實驗對象，其由兩個獨立驅動的后輪控制，完成姿態變化。在此基礎上，通過對差分驅動機器人運動學模型分析，設計了控制器并生成相應控制算法。利用仿真和硬件實驗平臺，在兩種不同運動情況下，完成對控制算法的驗證。仿真和實驗結果表明：位姿誤差收斂及速度收斂均能滿足一般跟隨控制需求，驗證了控制算法與控制器的有效性與穩定性。

此外，本文提出的控制策略易于實現，只需合理設置 λ參數即可完成對機器人編隊控制狀態的調整，可為多種復雜場合下實際應用提供有益借鑒。