五自由度機器人運動控制與空間位姿仿真系統

莊衡衡，丁 飛，章華濤，張海濤，暴建民

（1.南京郵電大學 江蘇省寬帶無線通信和物聯網重點實驗室，江蘇 南京 210003; 2.南京郵電大學物聯網學院，江蘇 南京 210003; 3.中國科學院國家天文臺南京天文光學技術研究所，江蘇 南京 210042; 4.中國科學院天文光學技術重點實驗室，江蘇 南京 210042）

0 引 言

隨著我國先進制造技術的發展，多自由度機器人以其自動化、高效化和智能化優勢，將在高端制造、空間遙操作和智能自主系統等領域獲得廣泛應用[1-2]。多自由度機器人的運動控制影響位姿的可達工作空間與目標指向精度[3]，兩者之間的有效協同將直接決定多自由度機器人的工作性能[4-5]。因此，研究并建立多自由度機器人的運動控制和空間位姿的協同分析與仿真系統具有重要意義。

作為機器人運動控制、位姿調整[6]的核心計算模塊，對正向運動學和逆向運動學的求解是關鍵。郭萬金等[7]針對一種五自由度機器人提出了逆運動學的封閉解法。張道義等[8]用矢量法和求導法分別對五自由度雕刻機末端運動學進行正向和逆向速度的分析。Cao F等[9]提出了一種基于SCARA的新型五自由度焊接機器人，采用DH模型得到正、逆運動學的一般公式，同時利用ANSYS軟件對其進行了模態分析。Lee J W等[10]指出工業機器人制造商和用戶大都專注于使用激光跟蹤器對機器人進行空間位姿精度測試。Zheng K等[11]對5-DOF混聯乒乓球機器人的機械臂進行空間位姿分析，將工作空間中的球拍姿勢轉換為聯合空間中驅動軸的參數，并使用ADAMS軟件進行運動模擬。

上述研究為多自由度機器人的運動控制與空間位姿分析奠定了良好基礎。本文提出一種五自由度機器人運動控制與空間位姿仿真方法，首先對五自由度機器人進行運動學建模，然后推導了其正向運動學和逆向速度運動求解方法，最后設計并實現了其運動控制與空間位姿協同仿真系統，為后續多自由度機器人的結構優化和可達工作空間分析提供分析平臺和理論支撐。

1 運動學建模與求解

1.1 五自由度機器人結構模型

本文的五自由度機器人結構模型如圖1所示，該機器人由三自由度的平動機構和兩自由度的轉動機構共同構成，其中前3個自由度分別定義為沿著X軸，Y軸和Z軸向的平動，O1、O2和O3分別為平動關節軸X軸，Y軸和Z軸上的關節節點，Ox,Oy和Oz分別為O1,O2和O3在各自平動軸上運動的起始點；根據平動關節軸的定義方向，后兩個自由度分別定義為沿著X軸和Y軸向的轉動，O4和O5分別為轉動關節軸X軸和Y軸向上的關節節點，c2，a4和b5分別為O1與O2，O3與O4和O4與O5之間的相鄰關節點的結構偏置，末端執行器安裝在關節節點O5上，在其上定義指向節點P，且兩個轉動關節軸的起始角度如圖1（a）所示。

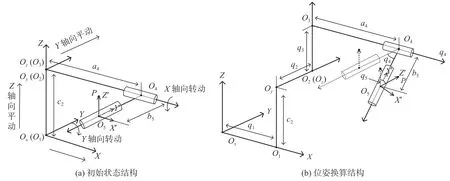
圖1 五自由度機器人的結構模型

為了方便描述經過五自由度的平動、轉動變后末端執行器的指向，在機器人的結構模型中定了2個坐標系，一個是基礎坐標系XYZ，另一個是過五自由度變換后的末端坐標系X′Y′Z′。其中義末端坐標系各坐標軸的正方向為基礎坐標系各標軸的正方向經過五自由度平動、轉動變換之后指向，且在末端執行器的初始位姿下，末端坐標與基礎坐標系的各坐標軸的正方向保持一致。關節點O1、O2、O3、O4、O5和P的位置均用基礎坐系描述，定義末端執行器的指向沿著末端坐標X′Y′Z′中Z′軸的正方向，因此指向節點P也定義在軸上，則末端執行器的指向沿著O5點到P點的方五自由度機器人的結構調整分別由各自運動上的高精度伺服電機驅動，均可在各自的運動軸沿著正、負兩個方向進行運動，且運動的正方向圖1（a）所示。通過對5個伺服電機的高精度協控制[12]，調整五自由度上機械臂的位姿，從而實機器人末端執行器的位姿控制與精確對準。

1.2 正向運動學求解

正向運動學是在已知各關節點的初始位置、相鄰關節點間的結構偏置等參數的前提下，結合相關節點間的相對運動量，求解末端執行器位姿的程[13]。在平動關節軸X軸，Y軸和Z軸上分別調整q2和q3的位移量，轉動關節軸X軸和Y軸上分別調q4和q5的旋轉量，經過五自由度的平動和轉動變調整后的狀態模型如圖1（b）所示。

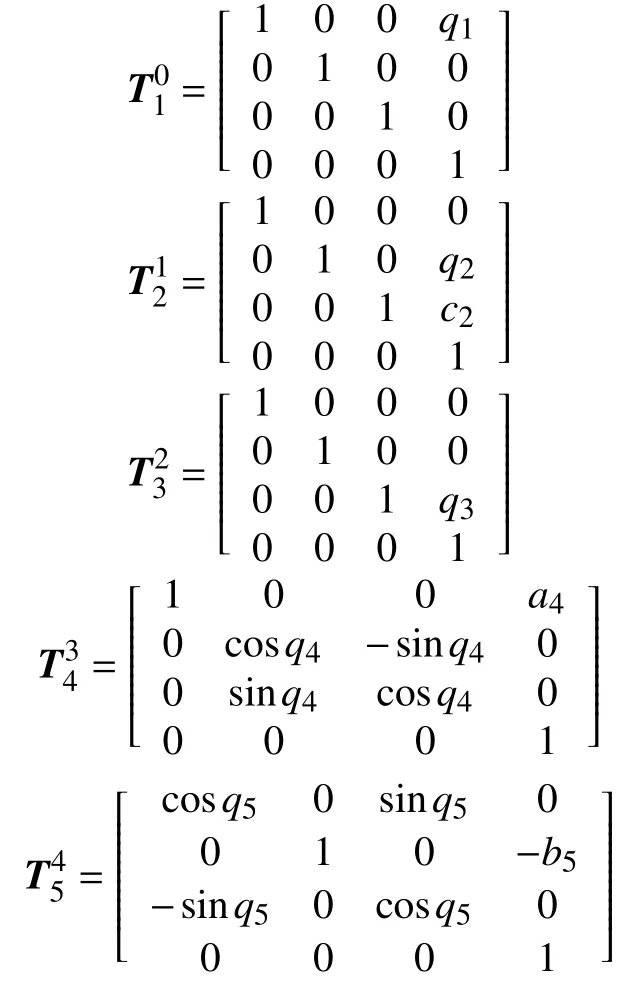
將上述矩陣依次相乘，得到末端執行器相對于基礎坐標系XYZ的等價齊次變換矩陣：

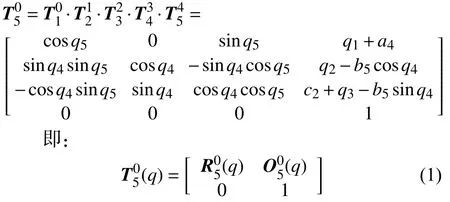
其中，相鄰關節點間的相對運動量向量為：q=（q1,q2,q3,q4,q5）T；旋轉矩陣為：

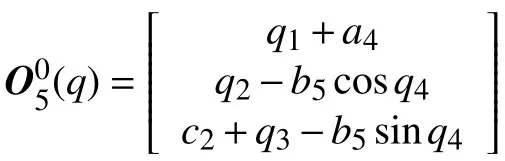
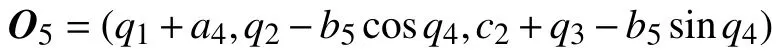
而末端執行器上的指向節點:

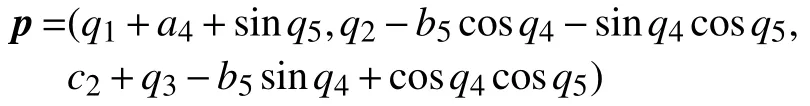
根據O5點的坐標和O5點到P點的指向，即可確定末端執行器相對于基礎坐標系的位姿：

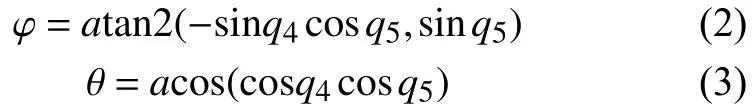
當使用ZYZ型歐拉角來描述末端執行器的指向時，在不考慮最后一個旋轉軸Z軸自轉的情況下，目標指向在地平式坐標內的方位角如公式（2），Z軸沿逆時針方向旋轉為正；目標指向在地平式坐標內的天頂距如公式（3），Y軸沿順時針方向旋轉為正。

1.3 逆向速度運動學求解

逆向運動學是通過末端執行器的當前位姿和目標位姿，反解出相鄰節點間相對運動量的過程[14-16]。與速度運動學相結合[17]，就是在已知末端執行器當前位姿和目標位姿的前提下，將末端執行器由當前位姿向目標位姿運動時的線速度和角速度與關節速度矢量聯系起來，并把關節速度矢量乘以電機的掃描時間間隔作為各個關節的調整量。

已知當機器人移動時，關節變量和末端執行器的位置都將是時間的函數。而角速度只要是相對于同一個坐標系來描述，就可以作為自由矢量相加，因此通過表示每個關節在基礎坐標系上的角速度，相加來確定末端執行器相對于基礎坐標系的角速度。結合本文的五自由度機器人結構，在使用ZYZ型歐拉角的旋轉軸定義，且不考慮最后一個旋轉軸 Z軸自轉的情況下，末端執行器相對于基礎坐標系的總的角速度矢量：

當末端執行器的目標位姿是固定值時，目標指向的速度方向向量恒為零向量，則當前指向調整到目標指向所需要的方向向量就是目標指向和當前指向間的方位角誤差，且在一定的時間間隔內計算時，可以把所有的距離變量當作速度值。

那么末端執行器的線速度：

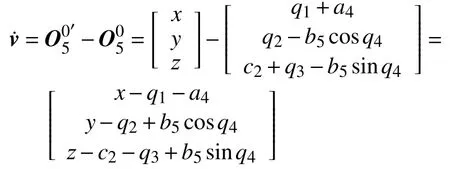
綜上，得到表達式：

其中Jv和Jω都是3×5的矩陣，5表示機器人結構中共有5個自由度，因此得到速度運動學方程[18]：

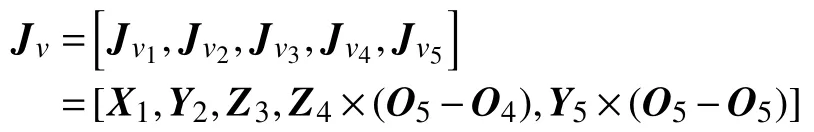
雅可比矩陣的下半部分Jω由下式給出：

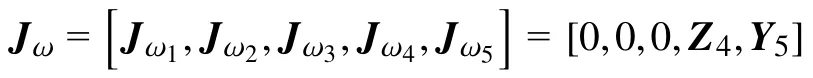
其中前3個平動關節對應的Jωi=0，后2個轉動關節對應其各自運動軸的單位方向向量。

綜上，根據速度運動學公式得：

其中J?為雅可比矩陣的偽逆矩陣，代入計算出，即五自由度上的速度調整量，用乘以電機的掃描時間間隔得到5個電機對應的運動調整量。

2 空間位姿仿真設計

五自由度機器人運動控制與空間位姿仿真系統的邏輯框架如圖2所示，該系統從功能邏輯上分為控制側與仿真側，其中控制側的主要功能為多自由度驅動單元的協同控制，核心的計算模塊是對正向運動學和逆向速度運動學的求解，從而確定末端執行器的當前位姿和向目標位姿調整時多自由度驅動單元各自的調整量，最后當調整后的位姿與目標位姿之間的相對誤差超過預設的誤差量級時，觸發位姿反饋。仿真側的主要功能是對控制側的特定業務流程進行數據同步，再對末端執行器當前的初始位姿進行計算，同時對動態調整過程中的階段性位姿進行在線仿真，最后對目標位姿進行誤差校驗與評定。

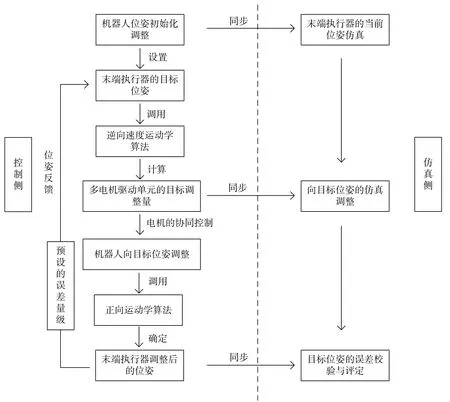
圖2 仿真系統的邏輯框架

五自由度機器人位姿初始化調整的業務流程如下：

1）控制程序調用各電機驅動器的驅動接口，與5個高精度伺服電機建立通信連接。

2）連接完成后，程序讀取伺服電機的輪上碼值，并進行硬件定義上的回原點，調整后通過正向運動學算法，計算出末端執行器的當前位姿。

3）程序調用逆向運動學算法，控制末端執行器運動到初始工作位姿（軟件定義上的回原點）。

五自由度機器人位姿仿真過程如下：

1）控制程序讀入末端執行器的目標位姿，調用逆向速度運動學算法，計算出五自由度上電機各自的調整值。

2）通過標準化控制接口，傳輸控制信號給5個伺服電機。

3）電機運動完成后，進行位姿校準，程序讀取電機的輪上碼值，調用正向運動學算法，確定末端執行器調整后的位姿。

在上面的執行過程中，如調整后的位姿與目標位姿之間的相對誤差超過預設的誤差量級，此時將觸發位姿反饋，重復上述操作直至調整后末端執行器的位姿符合預設。

3 實驗與分析

五自由度機器人的運動控制軟件采用Visual Studio開發環境，集成了Matlab軟件開發的末端執行器的位姿在線仿真平臺，兩者之間協同完成仿真任務。仿真實驗時，可以給定一組結構參數：c2,a4,b5分別取1.115 m,0.340 m，?0.145 m，選取一個馬鞍面作為五自由度機器人的作業任務面進行運動控制與位姿仿真，其數學方程為：

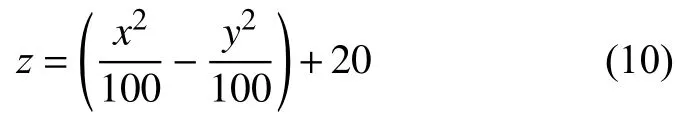
其中，取值范圍：?0.400 m≤x,y≤0.400 m，Δx=Δy=0.020 m。

圖3為根據馬鞍面數學方程得到末端執行器的目標位置仿真圖。末端執行器的指向取目標位置所在XY平面內的原點到目標位置的方向，此時末端執行器的位姿空間分布如圖4所示，俯視圖如圖5所示，其中相鄰且顏色不同的兩個點間的方向構成了末端執行器的指向。

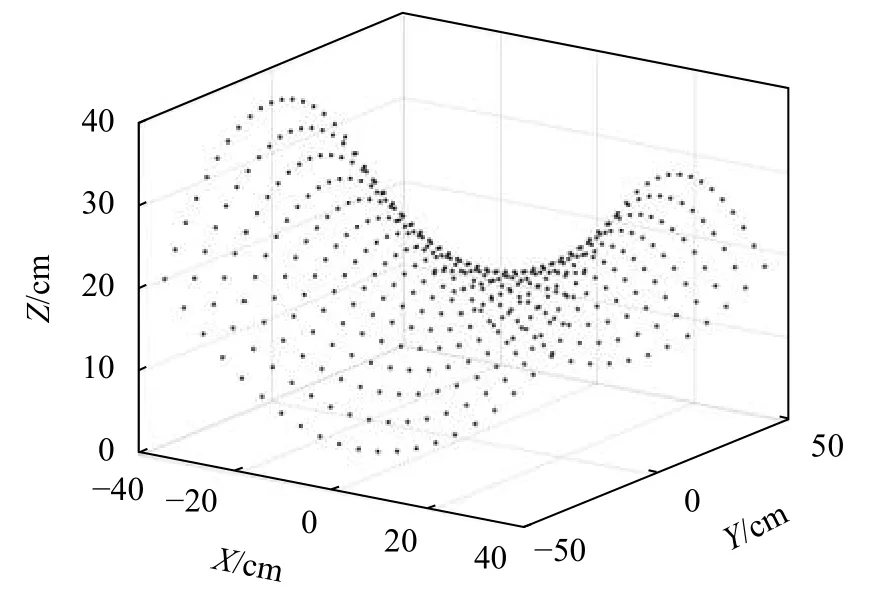
圖3 末端執行器的目標位置仿真圖

圖4 末端執行器的空間位姿仿真圖

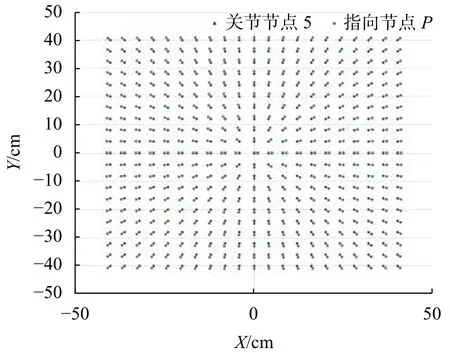
圖5 末端執行器位姿仿真俯視圖

定義末端執行器目標位姿的位置（Tx,Ty,Tz）和指向（Tφ,Tθ），調整后末端執行器位姿的位置（Cx,Cy,Cz）和指向（Cφ,Cθ）。當末端執行器調整后的位姿與目標位姿之間的誤差≤10?4m時，視為調整完成，此時定義對應點的位置誤差Δd和指向誤差Δδ分別為：

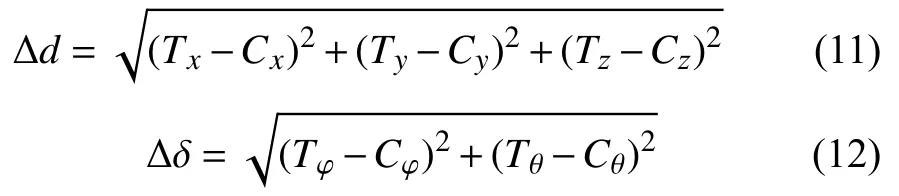
計算得到仿真位姿最大的位置誤差為：Δd=3.624 159 774 613 950×10?13m，指向誤差為：Δδ=1.998 894 815 878 120×10?14rad，發現兩者相對誤差非常小，因此該數值驗證了所提出的正向運動學和逆向運動學解法正確有效。

對五自由度機器人進行運動控制與空間位姿仿真，通過控制程序，調整末端執行器到達預設的起始工作點，末端執行器起始位姿和目標位姿的參數如表1所示。

表1 末端執行器起始位姿和目標位姿的參數

五自由度機器人的空間位姿仿真結果如圖6所示，圖中展示了對機器人三次靜態位姿下各個關節節點和指向節點的位置，其中指向節點上的數字0、1和2分別表示位姿調整的次數，第0次表示機器人的起始結構位姿，則末端執行器由起始位姿向目標位姿共調用運動學算法并調整了2次。計算第2次調整后相應的位置誤差與指向誤差，誤差結果均為0，結果表明該機器人運動控制與空間位姿仿真系統準確有效。

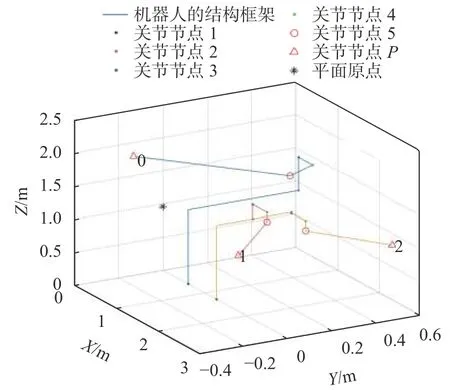
圖6 五自由度機器人空間位姿仿真圖

4 結束語

本文設計并實現了一款五自由度機器人運動控制與空間位姿仿真系統，針對五自由度機器人進行運動學建模，提出了正向運動學和逆向速度運動學求解方法，并選取馬鞍面為作業任務面進行在線仿真，數值計算結果表明末端執行器的仿真位姿與目標位姿具有一致性，驗證了仿真系統的可行性與工作穩定性。該仿真系統可實現五自由度機器人的運動控制與位姿仿真的一體化，為后續多自由度機器人的結構優化、可達工作空間分析與性能評估提供平臺支撐與技術基礎。