5R串聯機器人運動學分析及其控制系統研究

李國洪，周琪鈞

（天津理工大學 天津市復雜系統控制理論及應用重點實驗室，天津 300384）

0 引 言

工業機器人作為一種經典的機電一體化機械數字裝備，體現著人類智慧與機器人技術的發展成果，可實現生產制造的模塊化、智能化，技術附加值高，應用范圍廣。作為信息化社會的新興產業和先進制造業的支撐技術，全球各國都將其視為工業自動化發展的重點方向，勢必將對未來生產生活和社會發展起著愈發重要的作用。

在工業機器人的運動控制方面，國內外眾多學者都進行了廣泛的研究。如Metin Toz[1]最新研究了一種基于混沌理論的全新渦旋搜索算法來求解帶偏置腕的串行機械臂逆運動學問題，該算法具有較好的逆解尋優精度和收斂速度，但目前還停留在理論仿真尚未應用于實際。Matulis Marius和Harvey Carlo[2]利用數字孿生建模技術通過強化學習方式對機械臂進行虛擬現實分析，將數字世界與實體世界進行了完美融合。在國內，肖國紅等人[3]開發了一款基于PLC控制的5自由度機械臂實驗平臺，該平臺具有底座旋轉、垂直與水平移動、手爪旋轉與抓取等5個自由度。朱鵬程等人[4]運用Arduino控制器設計了一款五自由度機械臂與LabVIEW上位機，該系統可實現五自由度機械臂的基本功能，解決了實際本體實驗成本較高的問題。相較于國內，國外研究者不論是算法還是研究方式均領先我國，再者我國機器人研究人才缺口巨大，高校還是采用傳統大型工業示教系統的教學方式讓學生普遍有畏難情緒，且系統本身也具有一定的危險性，學生的學習積極性并不高，所以，開發一種經濟性、直觀性好的工業機器人控制試驗系統具有很強的現實意義[5]。

本文根據工業生產中5R（轉動副）工業機器人結構特點，首先采用DH參數法建模，建立起工業機器人運動學模型，采取坐標變換矩陣推導出機器人運動學方程，進行正逆運動學求解，運用Matlab軟件中的Robotics Toolbox進行機器人工作空間和軌跡規劃的仿真求解。最后通過搭建基于STM32F407的機器人控制系統與PC上位機進行實物聯合試驗，進一步驗證了運動學模型的正確性和機器人控制系統設計的合理性。

1 機器人DH參數建模

本文搭建的是5R抓取機器人系統，該系統的末端執行器具有5個自由度，即n末=5。其中，從下往上數的前3個轉動關節主要控制執行器的空間位置，而后2個轉動關節主要控制執行器的姿態，通常來講，控制執行器抓手開合的自由度一般不包含在n末中。圖1所示為5R抓取機械臂的DH坐標系機構圖。

抓取機械臂可以視為是一系列由運動關節串接起來的連桿組成的，為每一連桿構建一個坐標系，并用齊次變換來描述這些坐標系之間的相對姿態和位置。本文5R機械臂DH參數如表1所示。

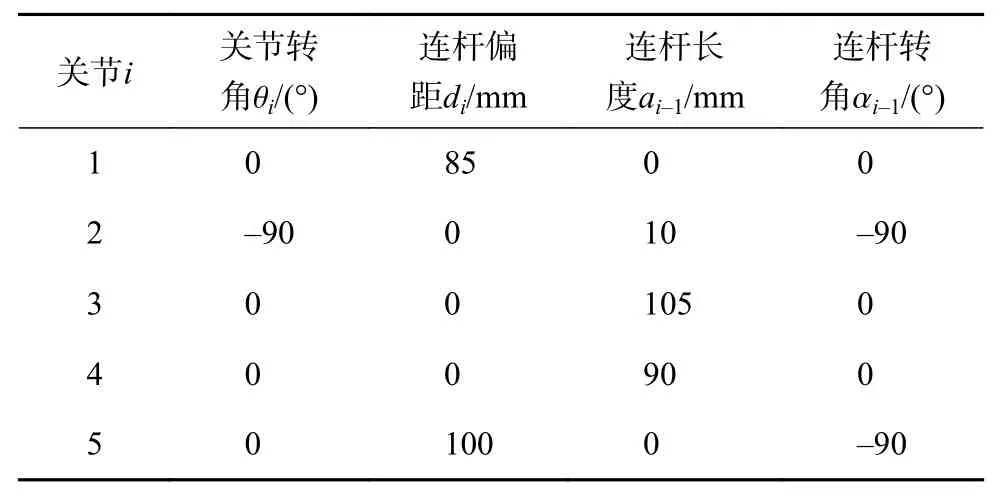
表1 5R機械臂DH參數

由于Matlab擁有強勁的矩陣運算能力和特有的Robotics Toolbox，采用該工具箱中的Link函數和Robot函數即可構建機械臂各個關節的模型方程，該函數的一般表達式為：

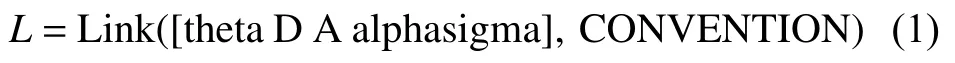
使用Robotics Toolbox中的Link函數創建該機器人的命令為：

L1 = Link（[0 85 0 0 0],‘modified’）；

L2 = Link（[–π/2 0 10 –π/20],‘modified’）；

L3 = Link（[0 0 105 0 0],‘modified’）；

L4 = Link（[0 0 90 0 0],‘modified’）；

L5 = Link（[0 100 0 –π/20],‘modified’）；

robot = SerialLink（[L1,L2,L3,L4,L5]）；

robot.name = ‘5R抓取機器人’；

robot.plot（[0,–π/2,0,0,0]）；

robot.display（）；

運行如上Matlab代碼后，即可獲得如圖2所示的機械臂模型圖[6]。若加入teach指令，則可通過左側滑竿框調節各個關節的角度位置，實現姿態調整，如圖3所示。

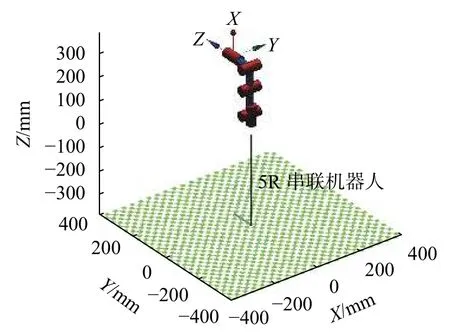
圖2 機械臂DH參數模型姿態圖

圖3 姿態調整圖

2 機器人運動學分析

2.1 5R機械臂正運動學分析

已知機械臂各個關節的轉動角度，求取機械臂工具端OT的姿態和位置，即為機械臂的正解。用坐標變換來描述從坐標系0～0T5的變換。由圖1可知，從坐標系1到坐標系0的變換矩陣為0T1。以此類推1T2、2T3、3T4和4T5。

已知相鄰連桿i與i–1之間的連桿變換通式為：

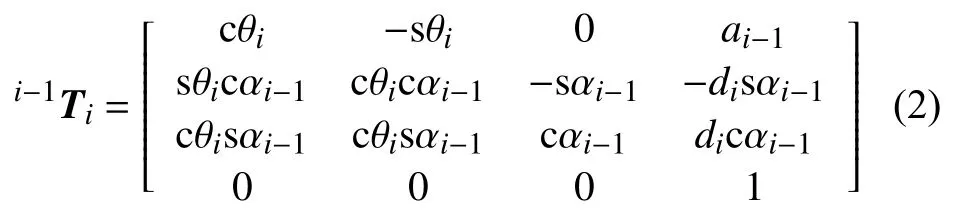
其中，s和c分別表示三角函數sin和cos。

根據連桿變換的齊次矩陣式（2）和表1的連桿參數，運用D-H法求得各連桿變換矩陣如下：

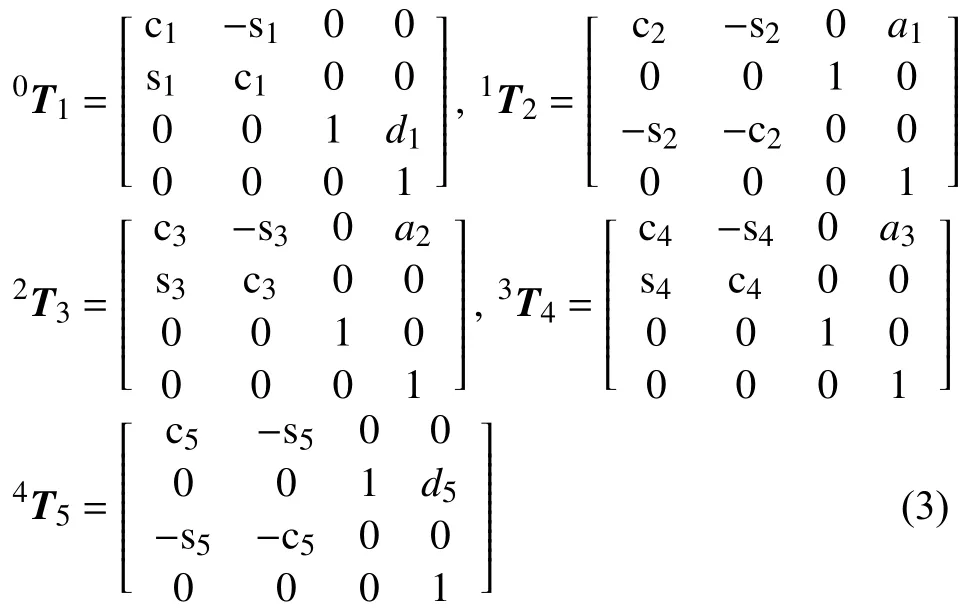
其中，ci=cosθi、si=sinθi。

5R機械臂的運動模型是由以上5個坐標變換矩陣相乘得到的，這樣即可得到該機械臂的運動學模型：

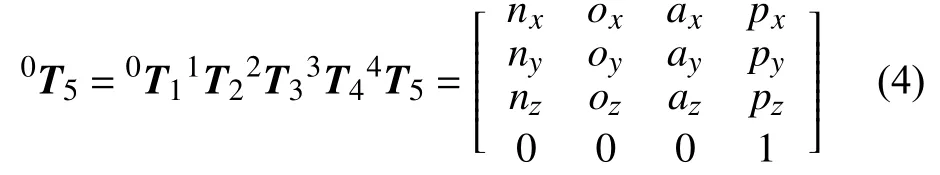
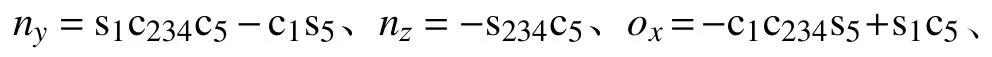
機械臂末端位置方程為：

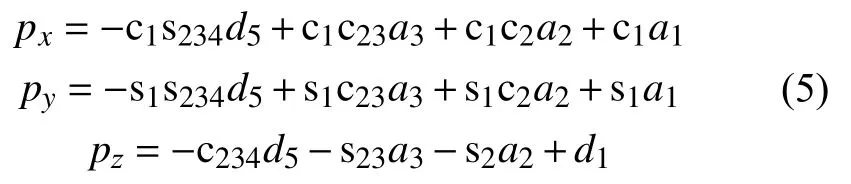
其中，sij=sin（θi+θj）、cij=cos（θi+θj）、sijk=sin（θi+θj+θk）、cijk=cos（θi+θj+θk）。

2.2 5R機械臂逆運動學分析

逆向運動學分析指已知末端執行器（機械爪）位姿的前提下，求解運動方程，即求得機械臂相應各個關節角度。這對于機械臂的運動控制至關重要。根據0T5可以知道機械臂的運動位置和姿態，需要獲得各關節的坐標值，用以機械臂能夠被驅動至這個位姿。

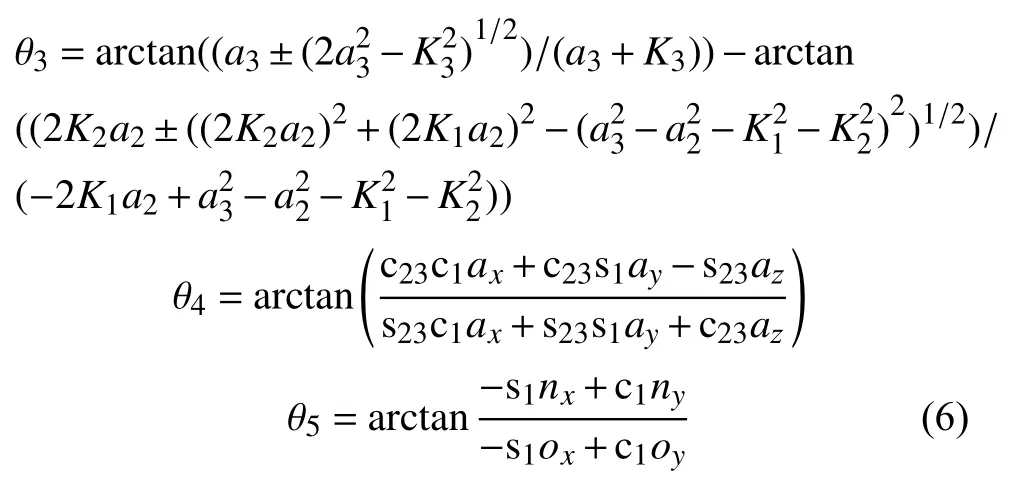
其中，K1=c1px+s1py?a1?d5c1ax?d5s1ay、K2=pz?

d1?d5az、K3=c1px+s1py?a1?a2c2?d5（c1ax+s1ay）+d5az+d1?pz?a2s2。

根據上面各式的結果來看，機械臂的運動反解可能存在多種解。但由于機械臂結構的約束，例如各關節變量可能不會全都在360°范圍內可運動，有些解不可能實現。在其存在多種解的情況下，應擇其最滿意的一組解，例如：選擇一組與機械臂當前位置最接近的解，或者考慮避障要求等，以滿足機械臂實際工作需求。

3 機器人運動學仿真

3.1 機械臂工作空間仿真

通常來講，機械臂的工作空間指的是末端執行器經歷所有可能的運動后末端遍歷的全部體積，它是衡量一款機械臂工作能力的一項重要運動學指標。將本文5R機械臂的工作空間記為S（P）。則工作空間和各個關節變量的關系可以用下式表達：

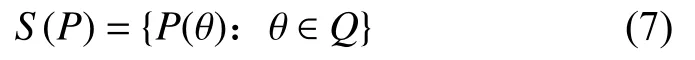
式中：θ=[θ1，θ2，θ3，θ4，θ5]——關節變量；

Q——約束空間，切莫隨意取值，應考慮實際情況確定約束空間：

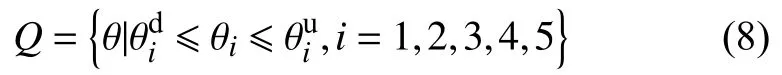
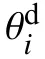
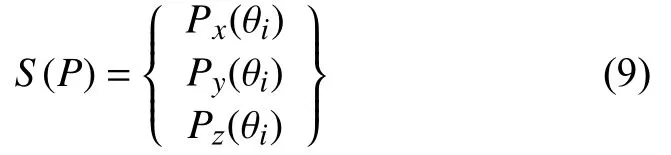
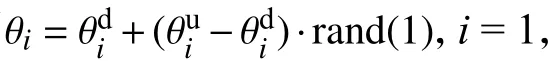
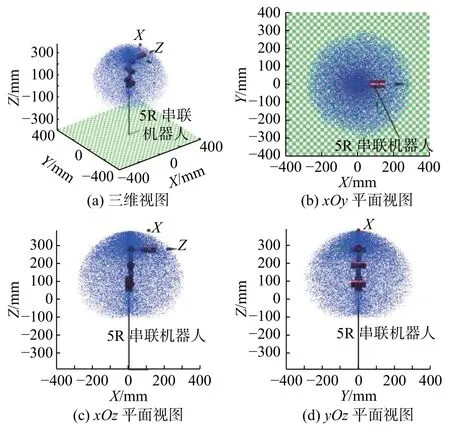
圖4 機械臂工作空間云圖

由圖4可以直觀地看出，機械臂在笛卡爾坐標系中三個方向上的運動基本上可以達到最大范圍內的所有空間。在實際的生產作業中，根據機械臂的位置數值可以分析得到其工作空間的邊界條件繼而知曉其運動范圍，通過將機械臂及相關工件進行合理配置，可實現場所利用率的最大化利用。

3.2 機器人軌跡規劃仿真

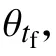
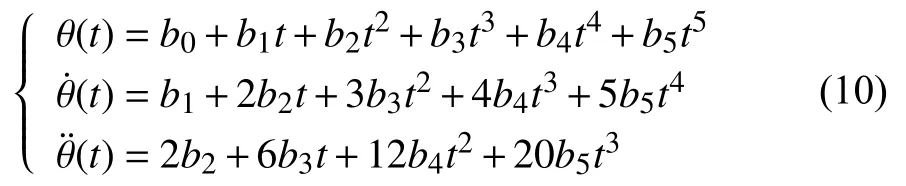
根據以上邊界約束條件，即可得到插值函數中b0～b5各值。

jtraj函數調用的格式為：[q qd qdd]=jtraj（qz,qr,t）其中，q為關節位置，qd為關節角速度，qdd為關節角加速度；qz為初始位置關節角的值，qr為終止位置關節角的值，t為軌跡運行的時間。

本文規劃的路徑軌跡是從 q1=[0，–π/2，0，0，0]運動到 q2=[π/2，–π/3，–π/4，–π，0]的曲線。

則有 qz=q1，qr=q2，設定時間t=[0∶0.1∶5]，總運行時間為5 s，采樣周期為0.1 s。

對該機械臂各關節角度位移、速度及加速度進行規劃仿真，可得到各關節物理量（角位移、角速度、角加速度）隨時間的變化曲線和軌跡路徑如圖5所示。

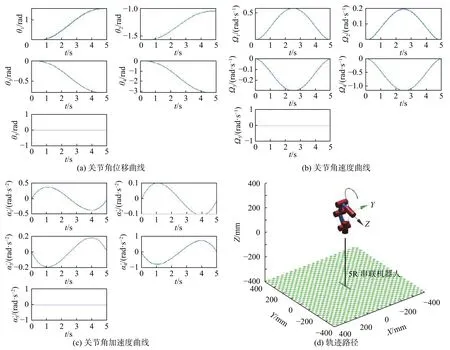
圖5 機械臂關節角位移、角速度、角加速度變化曲線及軌跡路徑

由圖5可以觀察到各個關節三個物理量（角位移、角速度、角加速度）隨時間變化的情況。從三幅圖中可以直觀地看到每個關節獨立運動互不干擾，并且各關節起點和末點速度與加速度為零，軌跡保持平滑連續。

4 機器人控制系統設計

4.1 控制器系統電路設計

以STM32F407嵌入式單片機為核心，設計了控制機械臂六組電機（包括工具端執行器電機）的硬件電路。該電路包含STM32F407最小系統、JTAG調試電路、芯片供電電路、濾波電路、FLASH存儲電路、USB轉串口電路、電機接口電路、RS485和CAN通信電路、按鍵、蜂鳴器和LED指示燈電路等。硬件電路原理圖由Altium公司發布的 Altium Designer（in AD19）軟件設計。控制系統框圖如圖6所示。

圖6 控制系統框圖

4.2 控制系統軟件設計及上位機介紹

該控制系統采用C程序設計進行軟件開發，KEIL MDK5為開發工具。圖7為控制系統軟件流程示意圖，該流程主要由主程序和中斷服務子程序構成。主程序包含系統初始化、機械臂初始位姿設定及其控制參數初始化，系統初始化又包含LED和蜂鳴器初始化、定時器TIM初始化、ADC初始化、中斷配置和串口通信配置等。中斷服務子程序主要由3個中斷服務函數構成，包括判定電機供電是否正常的定時器中斷TIM2服務子函數、接收判斷PC上位機監控軟件指令的串口中斷USART1服務子函數和輸出電機控制PWM的定時器中斷TIM3服務子函數。在main函數主循環中，TIM2中斷優先級最高，全程一旦檢測到電機供電異常，蜂鳴器就會報警提示；串口中斷USART1優先級次之，其主要任務是接收并判斷上位機指令是否符合既定控制指令并將其提取出來；TIM3中斷優先級最低，其主要任務是將提取到的控制指令轉換為相應的PWM輸出，驅動機械臂對應關節運動，使之完成相應指令。

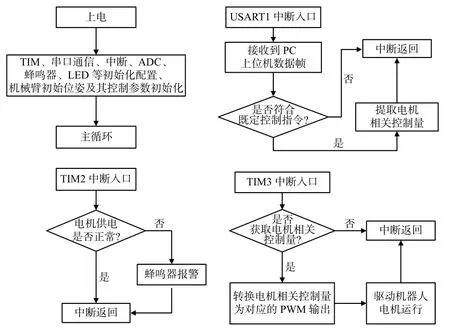
圖7 控制系統軟件流程框圖

PC上位機監控軟件采用微軟發行的Visual Studio軟件C#語言開發。軟件界面如圖8所示。采用上位機控制機械臂前，首先將micro-USB線纜連接控制板USB串口和計算機USB接口，再選定所用的串口號并設置好波特率后，即可對機械臂進行操作。該上位機設計有2種模式，分別為正、逆運動學演示模式。在正運動學模式中，上位機可以控制每臺電機的運動并且用戶能自主設計機械臂的運行動作；在逆運動學演示中，輸入起、終點坐標，機械臂可以平滑地由起點運行到終點，若運行不到或失敗，則有相應的警告提示，體現出逆運動學。

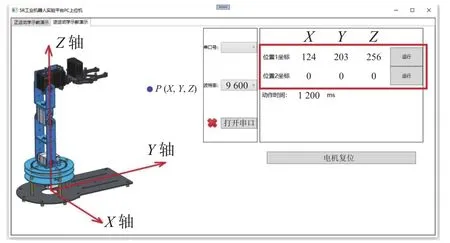
圖8 上位機監控軟件界面

5 系統試驗

根據上節所設計的機器人控制系統，完成機械臂與控制板及PC上位機的連接與安裝，圖9為STM32機械臂控制板實物圖，圖10為機械臂控制試驗系統連接圖。

圖9 STM32F4控制板

圖10 機器人控制系統連接圖

首先，連接機械臂與控制板。整個過程中要確保各連線準確無誤，同時保證電源開關等關鍵部件是否工作正常。當一切準備就緒后，則可對機械臂進行控制。

為了驗證前文所述軌跡規劃的正確性，設計一條從起點[0–π/2 0 0 0]運動到終點[π/4–π/2–π/2–π/3 0]的曲線。運用Matlab中所搭建的模型仿真，并取軌跡中的5個點為測試點，通過Matlab可獲得這5個點各自所對應的各電機角度理論值（見表2）。

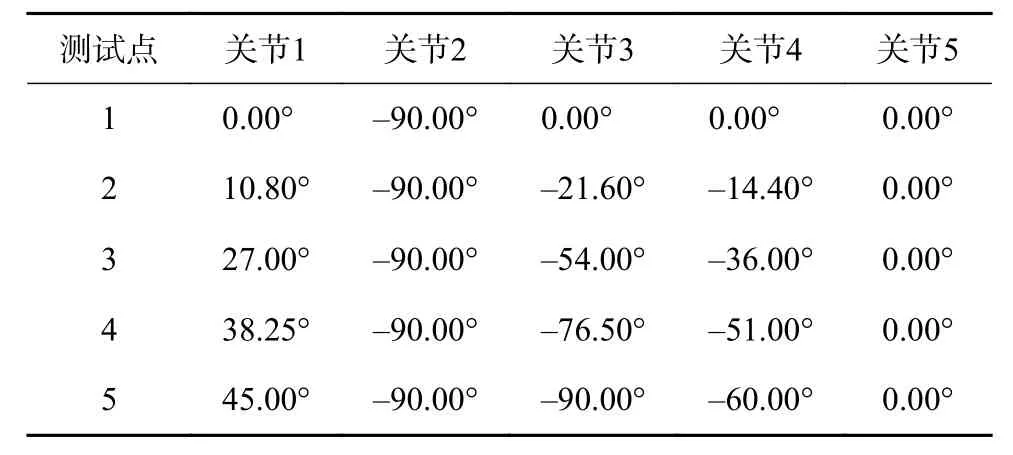
表2 測試點關節角度（Matlab獲得）

然后將這5個點換算成對應的空間坐標，輸入到PC上位機逆運動學界面的坐標輸入窗口中（見圖8），運行后可根據Visual Studio的控制臺窗口查看測試點所對應的各電機實際要驅動的角度（見表3）。通過將兩表進行對比，可發現各測試點仿真與實際中各電機轉動角度差別很小，考慮到系統開發過程中實物平臺的測量誤差和實物剛性的問題，可證明系統逆運動學編程開發的正確性和軌跡規劃的合理性。

表3 測試點關節驅動角度（Visual Studio算得）

整個試驗過程中，機械臂運轉正常，較準確經過所要求的路徑點，響應速度快，各關節之間運行平穩、連續無停頓，表明該機械臂控制試驗系統基本符合要求。

6 結束語

首先采用D-H參數建模法建立了工業機器人運動學模型，進而采用坐標變換矩陣推導出其運動學方程并進行正逆運動學求解。接著運用Matlab進行運動學仿真，根據Monte Carlo法和jtraj函數對機械臂的工作空間和軌跡規劃進行求解。在最后的實物驗證中，雖然試驗結果基本符合預期，但實驗過程都是在無障礙無干擾的理想環境中進行的，而實際情況并沒有這樣簡單，所以接下來的計劃是：1）在存在干擾因素的情況下對機器人進行軌跡規劃；2）解運動方程過程中若涉及方程非線性問題，可能導致無法推導出解析解，這時又應作何處理；3）文本研究的內容，暫不涉及動力學，而實際情況需將其考慮進去以達到更優的控制效果。