多傳感器異步融合算法AUV對接導航系統

夏 楠，曾慶軍，包靈卉，孫嘯天，許赫威

（1.江蘇科技大學電子信息學院，江蘇 鎮江212028; 2.中船海洋探測技術研究院有限公司，江蘇 無錫214142）

0 引 言

海洋資源豐富但環境復雜，AUV是探索和開發海洋的新型手段。隨著AUV的系統不斷升級，性能也在逐漸加強。目前AUV正在向著高自主、高性能、長時間、遠距離通信[1]等更智能方向發展。但是經過長時間工作，AUV需要精準的導航定位系統來引導AUV進行回收對接工作，方便布置新的使命[2]，和解決能源系統耗竭與提取內部數據的問題。

可靠的導航系統是AUV回收對接成功的重要保障。目前針對多傳感器在組合導航系統中采樣率不同的問題，幾乎都是建立在各傳感器數據傳輸都同步的理想狀態模型下，在單一尺度下對問題進行分析。但在實際情況中，組合導航系統中各傳感器的性能指標和采樣頻率各不相同，這就導致了多傳感器組合導航系統量測信息滯后的問題，即產生異步采樣問題[3]。因此對聯邦濾波結構中異步融合算法的研究，對AUV回收對接工作具有重要意義。

針對組合導航系統中多傳感器異步采樣問題的研究，文獻[4] 在組合導航系統中采用數據塊分析技術，并提出了一種異步貫序濾波算法，融合各尺度經KF濾波優化的局部狀態估計，最終得到全局最優狀態估計值。算法使用要求各傳感器的采樣率是2的整數倍，實際應用比較受限。文獻[5]提出多尺度數據分塊的組合導航算法，主要在最細尺度下的系統模型中利用數據分塊，將量測信息分解到各尺度進行濾波，得到全局最優狀態估計值。此方法雖然提高了導航精度，但是增加了系統的計算量。

本文為了提高由于采樣頻率不同而致導AUV在回收對接過程中的導航定位精度較低的問題，提出了一種基于UKF融合的多尺度異步融合算法。本文算法依據采樣率劃分多尺度信息，建立基于聯邦濾波的多尺度系統誤差模型，并針對不同尺度信息采用UKF算法進行非等間隔異步融合，從而得到全局的最優狀態估計。仿真表明，基于UKF的多傳感器異步融合算法對AUV回收對接導航系統中異步采樣信息具有更高的融合精度，提高了導航系統的精度和可靠性。

1 AUV回收系統原理

本文以江蘇科技大學自主研發的“探海I型”自主水下機器人（AUV）的回收對接系統為研究對象。根據AUV的運動特性，可以把整個回收對接過程分為直線歸位、直線跟蹤、直線對接與慣性對接4個階段。前面兩個運動對接階段的導航系統，為本文主要研究內容，此階段AUV采用組合導航的方式。未進入USBL的作用范圍時，主要由SINS的航位推算提供AUV的相對位置。當進入USBL的作用范圍時，用多傳感器融合的方式，提供AUV的相對精確位置，不斷地調整AUV的位置與姿態，使其運動軌跡在對接塢在中軸線附近。而后在距離較近的直線對接階段，采用雙目視覺導航，使AUV機身對在對接塢的中軸線上，最后進入慣性對接階段，依靠AUV運動慣性緩緩駛入對接塢。圖1為回收對接流程圖。

圖1 AUV回收對接流程框圖

如圖2所示為“探海Ⅰ型”AUV實物圖，其裝配的傳感器與相關參數如表1所示。

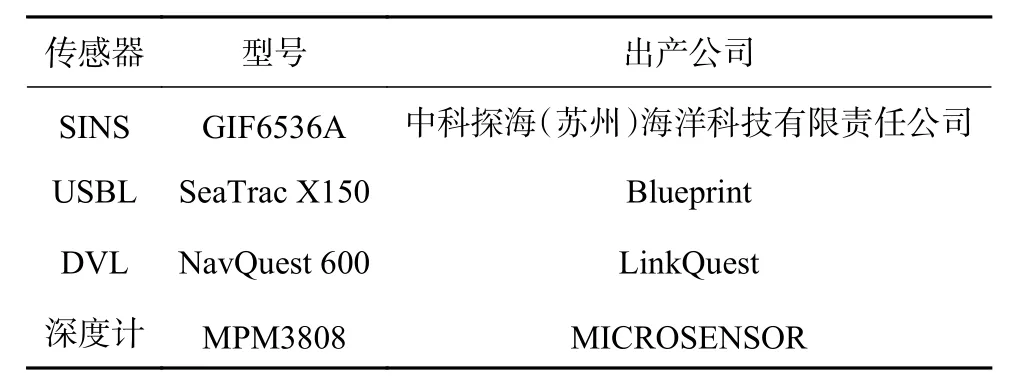
表1 傳感器及相關參數

圖2 “探海Ⅰ型”AUV

2 多傳感器組合導航系統建模

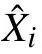
圖3 聯邦濾波結構圖

2.1 多傳感器組合導航系統狀態方程

選取導航系統的誤差作為狀態量，主要誤差包括速度、姿態、位置、加速度計零偏和陀螺漂移[7]，USBL/DVL/深度計分別提供位置、速度、深度信息作為輔助則系統狀態變量為：

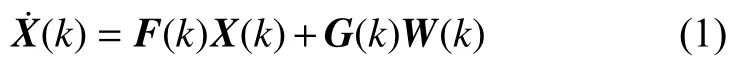
式中：F（k）——系統狀態轉移矩陣；

W（k）——過程噪聲矩陣；

G（k）——過程噪聲驅動矩陣。

其中子系統的狀態量X（k）為：

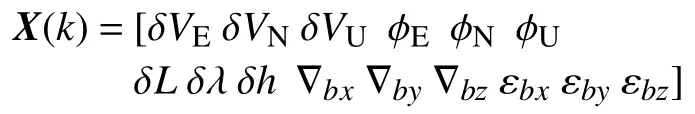
式中：δVE,δVN,δVU——東、北、天三個軸向的速度誤差；

φE,φN,φU——東、北、天三個軸向的失準角；

δL,δλ,δh——緯度、經度、深度誤差；

?bx,?by,?bz——加速度計三個軸向的隨機偏置誤差[8]；

εbx,εby,εbz——陀螺的三個軸向隨機漂移值。

由已知的系統誤差模型，可建立子系統的非線性系統狀態方程[9]為：

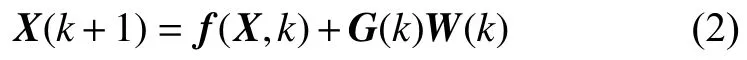
2.2 多傳感器組合導航系統量測方程

本文設計的多傳感器組合導航系統中，有3個子濾波器，每個子濾波器的量測方程：

1）取SINS位置數據與USBL轉換后輸出的位置數據作差為量測值，得SINS/USBL子濾波器量測方程：

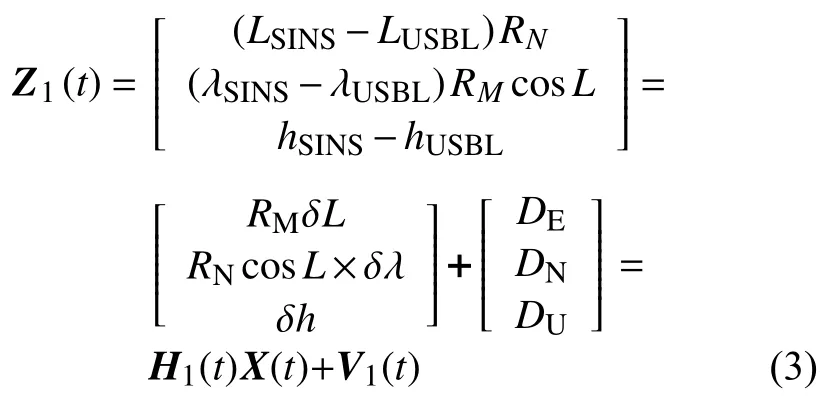
式中：LSINS，λSINS，hSINS——SINS的緯度、經度和深度信息；

LUSBL，λUSBL，hUSBL——USBL的緯度、經度和深度信息；

DE，DN，DU——USBL沿東、北、天方向的位置測量誤差；

RN——地球子午圈半徑；

RM——卯酉圈的曲率半徑[10-11]。

2）取SINS與DVL輸出的位置數據作差為量測值，得SINS/DVL子濾波器量測方程：

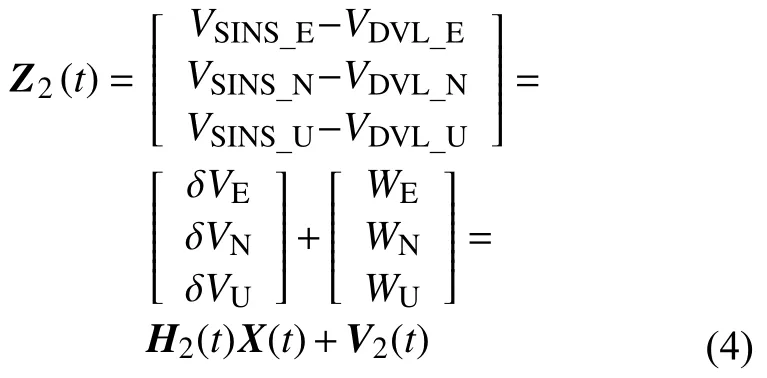
3）SINS與深度計輸出的位置數據作差為量測值，得SINS/深度計子濾波器量測方程：

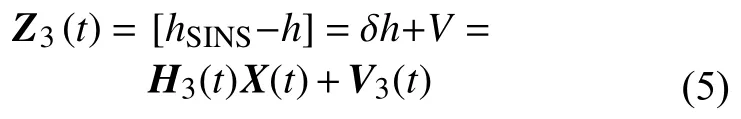
3 多傳感器異步融合算法

3.1 多傳感器多尺度系統模型

假設用i=1,2,···,N來表示N個傳感器，每個傳感器對應的采樣率為Ti，假設N為最細尺度，1為最粗尺度，ni∈N+，設傳感器i和j之間的采樣頻率之比為A，則A為任意正有理數，即

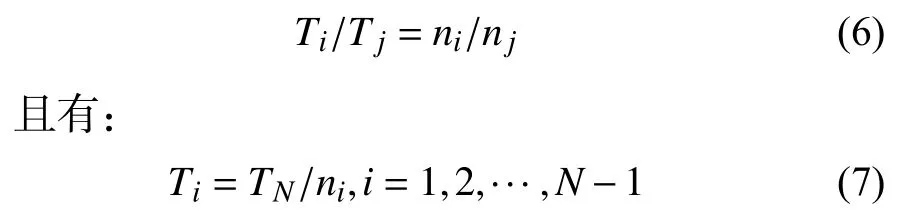
由多尺度模型分析可知，i表示傳感器所在尺度，同時也表示其位數。本文設計的多傳感器組合導航系統中，已知輔助參考系統在最高采樣頻率下的狀態方程和觀測方程[12]。第i=1個為低頻采樣傳感器在最粗尺度上，第i=N個為高頻采樣傳感器在最細尺度上。每個子傳感器所在尺度各不相同，建立系統模型為：

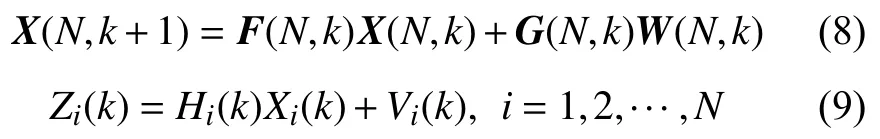
可得，尺度i上k時刻的采樣值與尺度N上nik時刻的采樣值相對應，即可表述為：

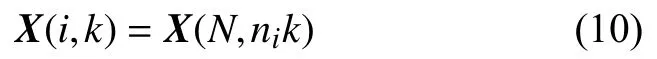
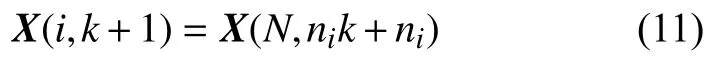
可建立尺度i上的非線性系統狀態方程和觀測方程：

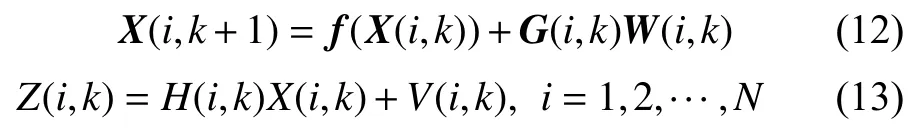
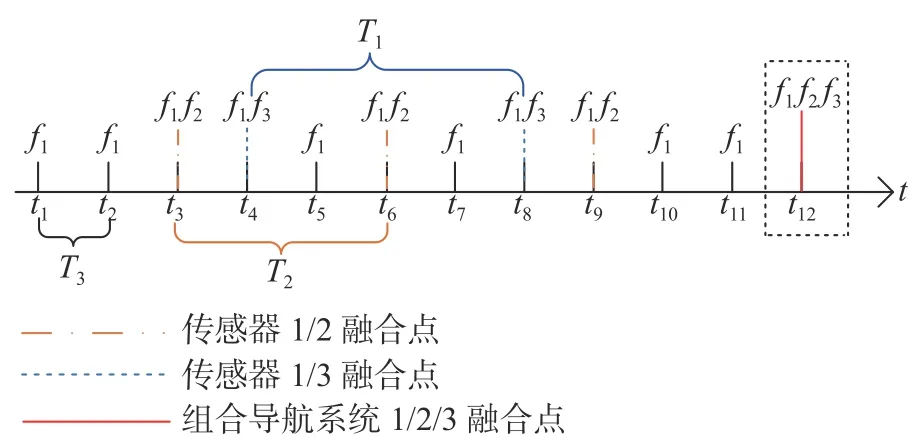
圖4 多尺度異步采樣示意圖

3.2 多傳感器異步融合算法建立

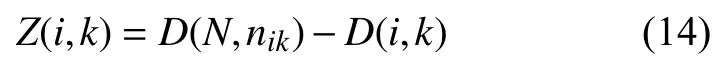
式中：D（N,nik）——nik時刻SINS的數據信息；

D（i,k）——尺度i上導航傳感器在k時刻的量測值。

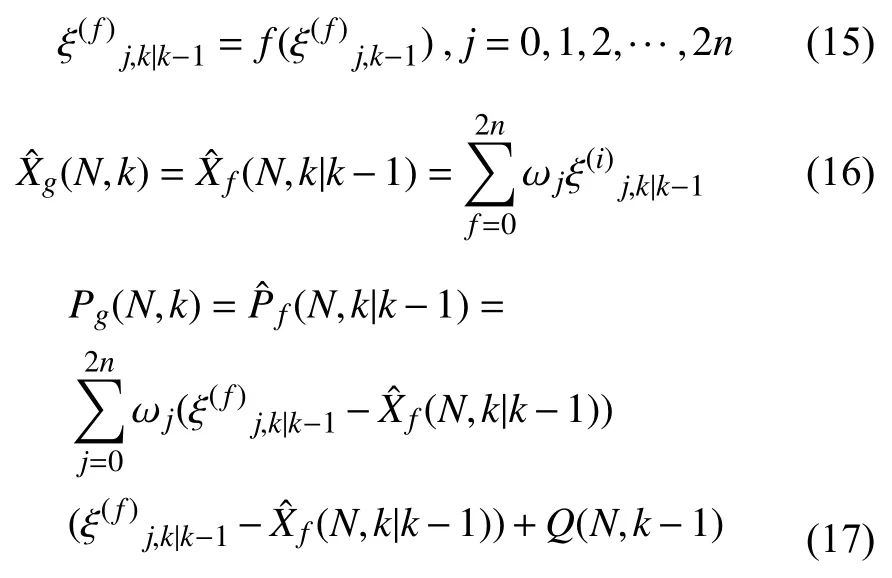
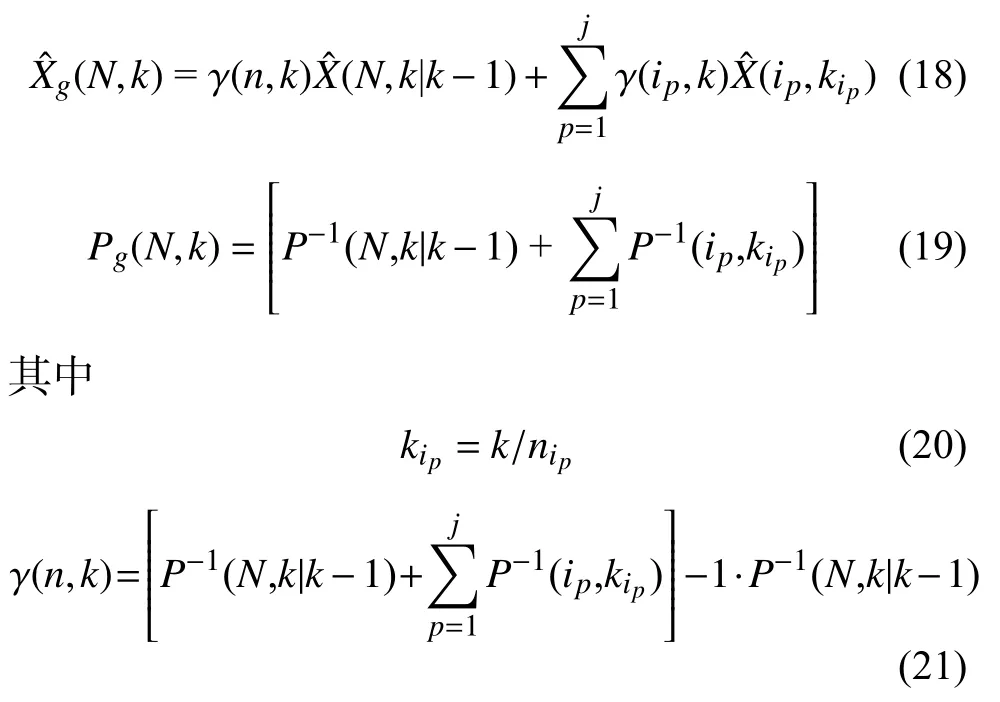
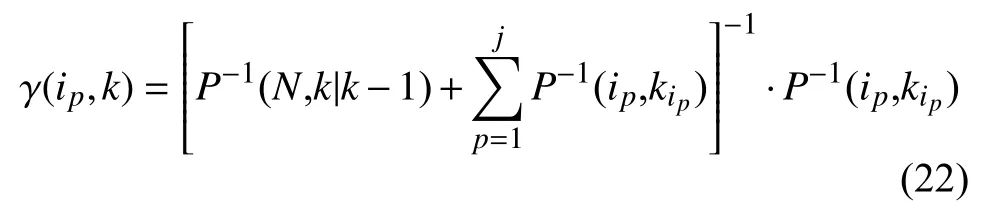
如圖5所示為AUV對接導航系統中異步融合算法流程圖。

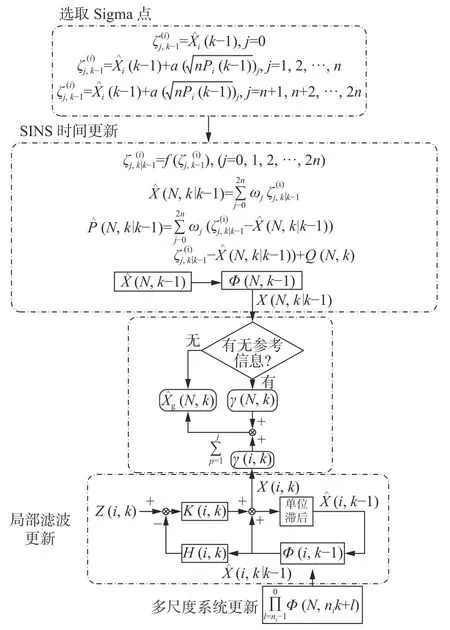
圖5 AUV多傳感器異步融合算法流程圖

4 仿真結果分析與湖試實驗

4.1 仿真結果分析

為了驗證本文設計的多傳感器組合導航異步融算法在AUV對接導航系統中的有效性，利用Matlab軟件進行仿真實驗。仿真系統中對AUV水下航行的動態軌跡仿真以及利用導航傳感器真實的誤差數據仿真生成動態數據。如表2和表3所示，為所用傳感器的誤差參數和采樣率。

表2 導航誤差參數

表3 各傳感器采樣時間

表2中，由于AUV使用的深度計為400 m級大量程，所以精度最高在米級。

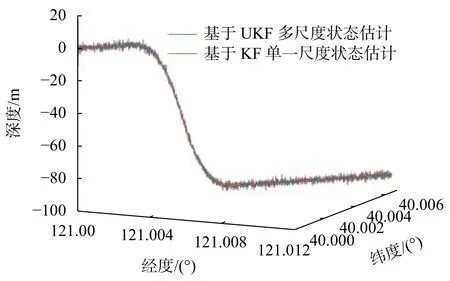
圖6 AUV運動軌跡及狀態估計

為了突出比較基于UKF的多傳感器異步融合算法的優越性，針對速度、位置在同一運動軌跡上的誤差，對三種不同的融合算法結果進行對比，表4所示為單一尺度狀態估計和多尺度兩種融合算法的狀態估計標準差對比，圖7為速度誤差對比，圖8為位置誤差對比。

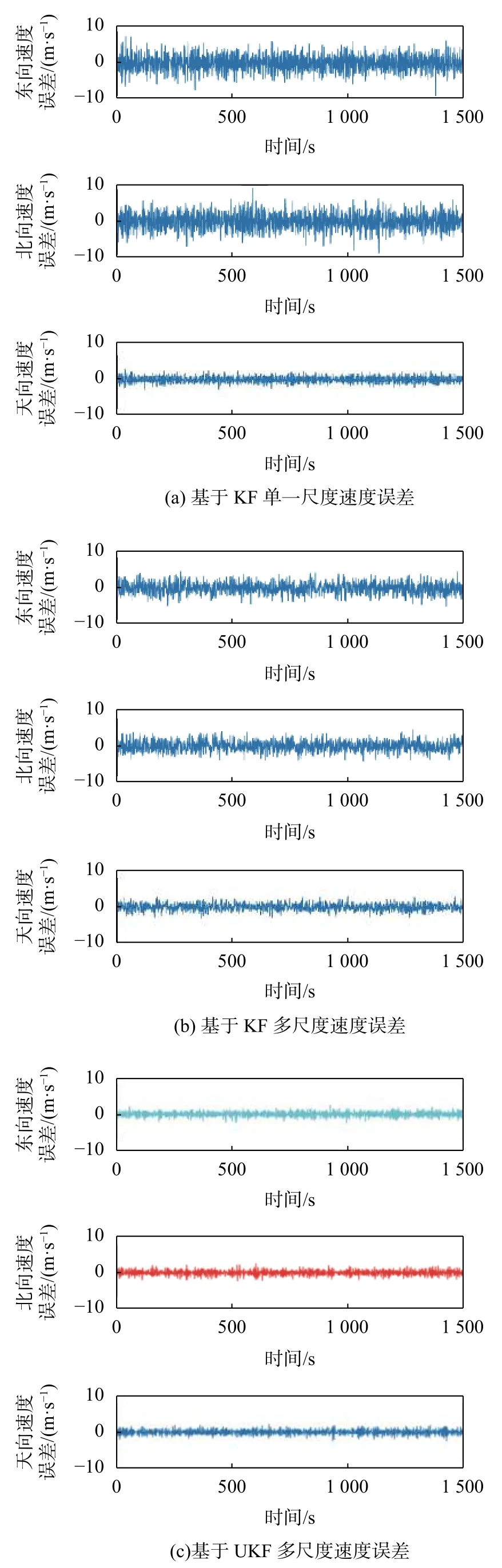
圖7 AUV運動速度誤差對比

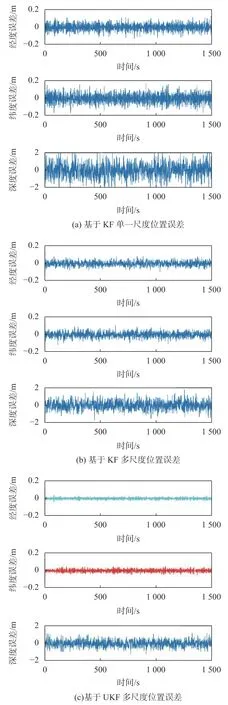
圖8 AUV運動位置誤差對比

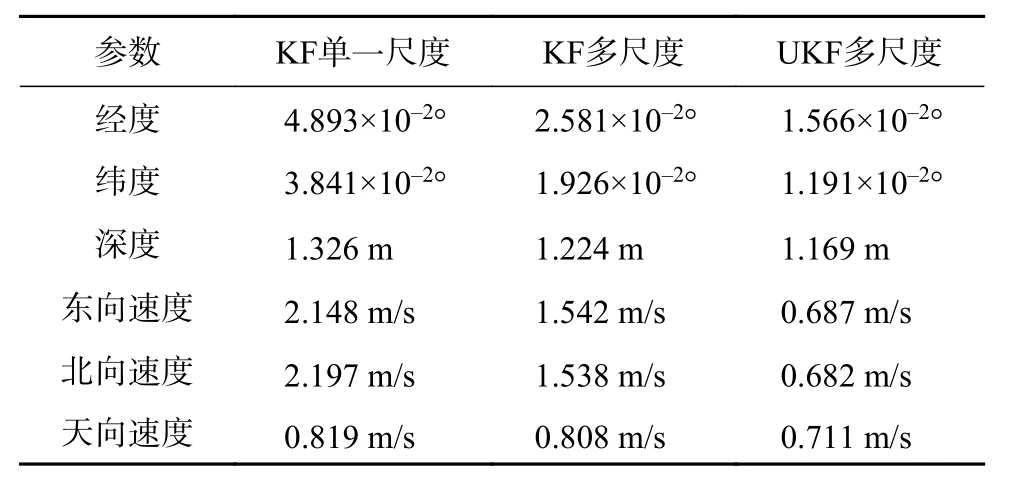
表4 各參數標準差對比

仿真結果顯示基于UKF的多傳感器導航異步融合算法相對于基于KF的單一尺度融合算法和基于KF的多尺度融合算法更加穩定，濾波精度更高。本文設計的算法，有效的解決了由于采樣頻率不同而導致多傳感器組合導航系統精度較低的問題，提高了AUV回收對接導航系統中異步采樣信息的融合精度。

4.2 湖試實驗

實驗地選擇在水域較為開闊的蘇州某湖進行，便于試驗開展，水深5～40 m，水流2節左右。如圖9，為回收對接過程，圖10為水面回收航跡圖，表5為實驗部分數據。

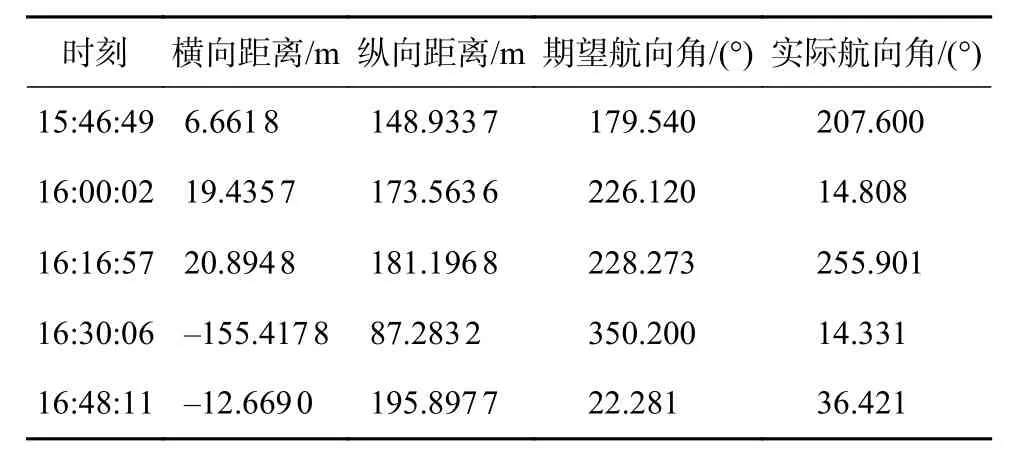
表5 部分實驗數據

圖9 回收對接實驗

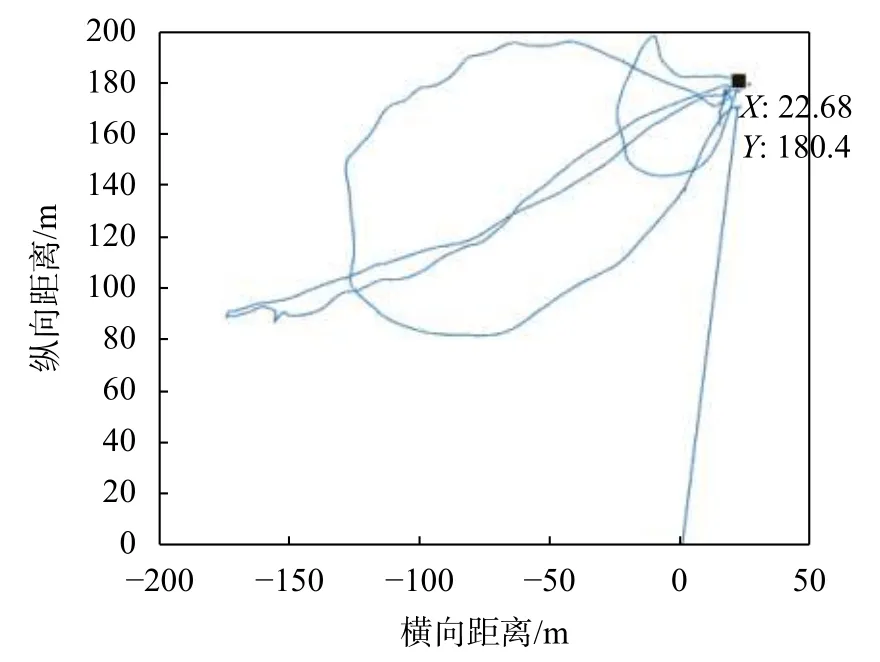
圖10 水面回收航跡圖

實驗將對接塢固定在岸邊碼頭，通過上位機規劃AUV的目標點和深度的使命，到達目標點后開始自主對接實驗。設置AUV速度0.8 kn（1 kn≈0.514 m/s），目標點坐標為（22,180），回收點坐標為（28.68,180.4），進行將近1.5 h的使命回收時間，對接實驗成功。實驗表明本文所設計的導航系統更加精準，在實際應用上為AUV的對接回收提供了安全保障。

5 結束語

本文為了提高由于采樣頻率不同而致導AUV在回收對接過程中的導航定位精度較低的問題，提出了一種基于UKF融合的多尺度異步融合算法。本文算法依據采樣率劃分多尺度信息，建立基于聯邦濾波的多尺度系統誤差模型，并針對不同尺度信息采用UKF算法進行非等間隔異步融合，從而得到全局的最優狀態估計。通過Matlab軟件針對實際系統進行仿真實驗，相比于基于KF單一尺度算法與基于KF多尺度算法，本文基于UKF的多尺度異步融合算法具有更高的濾波精度和實際應用價值。湖試實驗充分驗證了AUV對接導航系統的有效性。