計算機輔助設計凸輪輪廓線的方法研究

花 卉

信陽技師學院，河南 信陽 464000

凸輪從動件機構通常在絕大多數的機械系統中被采用，通過直接性表面接觸將所需的運動傳遞給另一個機械元件。凸輪和從動件機構非常方便而且簡單，它們之間很少有其他運動部件，所占據的空間非常小。一般來說，從運動學的觀點來看，凸輪機構由3個不同的基本部分組成：驅動元件、從動件、從動件和固定框架。凸輪機構通常在大多數現代機械機構中被廣泛應用，特別是在自動機械和儀器、內燃機和控制系統中應用最為廣泛。雖然凸輪機構的自動化程度相對來說比較低，但由于其制造成本較低而且能夠滿足幾乎任何從動件運動所需的一種最簡單結構，因此應用范圍較為廣泛[1]。

1 凸輪機構設計概況

凸輪機構設計包括兩個階段：首先，選擇滿足規定運動學規范的適當傳遞函數；其次，機構幾何優化，考慮構造約束。凸輪輪廓設計技術的發展通常基于樣條曲線的使用。凸輪的運動特性通過標準運動函數、拋物線函數、簡諧函數和擺線函數的組合來綜合應用。在過去，凸輪輪廓的設計是一項煩瑣的工作，需要應用圖形或分析方法[2]；而在當今的大多數應用中，凸輪輪廓是由數控銑刀加工而產生的，數控銑刀可以依據數控編程來切削凸輪輪廓，可以在不需要首先明確凸輪輪廓的情況下生成所需要的從動件運動軌跡。凸輪機械設計的一個重要特征就是在不同半徑的圓弧連接的切點處突然做加速度變化[3]。任何凸輪的輪廓取決于所需的從動件運動特性，通常以位移和速度屬性來表達。在自動車床的情況下，形成平面凸輪形狀的原始曲線（如螺旋形），通過車削具有所需尺寸和幾何屬性（如球形輪廓）的部件所運用的刀尖運動軌跡特性來控制。目前諸多文獻中有各種各樣的凸輪輪廓設計方法。

2 研究方法

文章通過凸輪輪廓線上3個連續點的矢量差的解析表達式，計算了從動件運動的凸輪廓線曲率。然后，采用類似的算法設計從動件的運動特性。根據凸輪輪廓上3個連續點的同一矢量模型的初等幾何，通過迭代過程計算速度、加速度和沖擊，呈現出了銑刀運動軌跡樣條線實時位置的效果，將矢量差的解析表達式計算結果輸出到數控編程運算程序中，開創了一種新的計算機算法。該方法適用于低速機械或低精度應用，或者機械設計尺寸減小到毫米（最小機構）甚至微米（微型機構）的情況。在這種情況下，多項式凸輪輪廓的制造變得困難，甚至更復雜也更難以驗證。該研究實例證明了該方法的工程可行性，并與凸輪從動件機構的解析設計參數進行了對比。

3 凸輪從動件運動分析的數值方法

任何凸輪的輪廓取決于所需的從動件運動特性，通常以位移和速度屬性表示。對于具有直線（平移）平面從動件的凸輪，如圖1所示，凸輪圍繞點OA旋轉，平面從動件始終移動，因此其幾何軸始終在OAB線上。Rb是基圓半徑。凸輪上的基準線從一固定點開始轉動到凸輪與從動件在A點接觸時所運動的時長t時，基準線所運動的角度為θ。

圖1 具有主動平面從動件和凸輪輪廓上3個連續點的凸輪

銑刀的半徑為Rc，中心在Oc點。S（θ）是從動件的位移距離與旋轉角度θ構成的一種函數關系。在銑刀運動過程中，凸輪軸在每個時間和每個角度上都可以按規定的角度旋轉OA，銑刀的中心可以編程設置為這樣一個位置，即從動件的位移將由功能S（θ）規定。因此，給定的數據是銑刀半徑Rc，凸輪中心的位置旋轉OA和每個角度所需的銑刀中心位置Oc（距離a等于半徑R加Rc）。假設凸輪dθ圍繞OA進行小的增量旋轉，從動件的中心線逆時針旋轉dθ。虛線表示從動輪的位置變化。向量R相對于中心線的位置是φ。

銑刀中心Oc的坐標計算如下：

點A的極坐標、凸輪和刀具的接觸點如下：

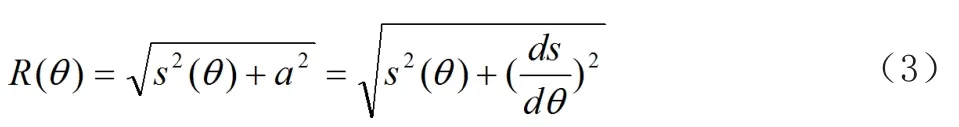
凸輪最小廓線曲率計算的解析式為

式中：Rb為基圓半徑；s(θ)為從動件的位移。

s(θ) 和導數s＇(θ)、s＇＇(θ) 的計算是一個煩瑣的過程，通常會導致很大的誤差，這取決于相應的時間增量。速度、加速度和沖擊的誤差分別與1/Δt、1/Δt2和1/Δt3成正比。根據從動件位移確定銑刀和凸輪表面接觸點近似圖形，采用近似數值方法計算凸輪輪廓曲率ρ。然后根據凸輪廓線確定從動件的速度和加速度屈服，并用圖形表示法幫助用戶接受或拒絕凸輪-從動件運動副的特性。

由于曲率中心在凸輪表面上是靜止的，凸輪輪廓曲率的大小和定義瞬時曲率中心的矢量不會因凸輪旋轉的微小變化而改變[3]，凸輪輪廓上的3個連續點位于半徑為ρ的圓的同一圓弧上，中心位于O（Xρ，Yρ），笛卡爾坐標為（Xi-l，Yi-l），（Xi，Yi），（Xi+l，Yi+1）。這些點屬于等角 AO 的連續半徑，每個弧的曲率根據畢達哥拉斯定理計算如下：

式中：xρ和yρ是弧中心的坐標。

式（5）屈服得到

根據式（6）得出xρ和yρ的坐標。然后計算凸輪輪廓曲率ρ，公式如下：

式（7）根據凸輪-從動件配置和數據庫[2]中可用的從動件位移的幾何關系，得出從動件運動位移s（θ）的凸輪輪廓曲率。對于凸輪輪廓上的3個連續點，角度Δθ等于360/N，其中N是構成凸輪輪廓的離散點的數目。對于大量的點N，Δθ變得非常小，然后考慮到時間的無窮小增量，凸輪輪廓的速度、加速度和沖擊度分別計算如下：

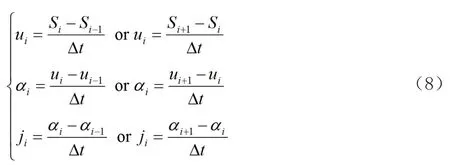
為了獲得更高的精度，式（8）將被視為

式（7）～式（9）確定了從動件位移、速度、加速度和沖擊以及凸輪輪廓曲率。利用上述公式，開發了凸輪從動件設計程序，用于計算凸輪從動件的設計參數。該算法綜合了凸輪-從動件運動副的各種構型和任意凸輪轉角下從動件位移的幾何關系。必須首先限制時間步長增量，通常是360度的倍數。然后，用戶從可用功能中選擇從動件運動特性，或提供特定從動件運動所需的數據。式（3）的解和所選時間步長對應離散點的限制需要此方程[3]。算法是將這些點的坐標存儲在一個特定的數組中。為了確定凸輪輪廓和速度、加速度和支撐配置，可通過式（7）和式（9）的解得出。由于該算法適用于低速運動副或低精度應用場合，與解析相比，1440點的離散化結果具有較高的精度。當然，離散化取決于所研究的特定凸輪-從動件副，并且該方法提供了壓力角和曲率半徑大小的適當檢查。以上從動件盤形凸輪機構為例說明了該方法的應用。首先，從合并的數據庫中選擇凸輪從動件結構和相應的從動件位移關系。從式（8）中獲得凸輪從動件位移、速度和加速度圖。然后，通常采用位移和速度的特點來表示從動件運動的特性。凸輪從動件運動特性繪制在通過擺線式從動件運動的分析方法計算的相應點上[4]。

4 結論

文章提出的算法是通過對凸輪輪廓上的3個連續點采用矢量差分算法來描述期望從動件運動的凸輪輪廓曲率的數值過程。通過一個類似的迭代過程，定義了從動件的運動特性（速度加速度、沖擊），并驗證了凸輪廓線設計的可接受性。數值算例驗證了分析設計方法的正確性，使計算誤差最小化，并證明了其工程可行性。