基于自適應Kriging模型的人行斜拉橋有限元模型修正*

秦世強，廖思鵬，黃春雷，唐劍

武漢理工大學土木工程與建筑學院，湖北武漢 430070

在結構設計、施工、養護管理等領域，建立能夠代表實際結構行為的有限元模型尤為關鍵［1］。由于建模過程簡化和誤差、結構參數的不確定性等因素［2］，導致有限元模型計算響應與實測響應之間存在一定差異；為此，通常需要對初始模型進行修正，從而獲得能夠代表實際結構的有限元模型。模型修正可看作優化問題，其目標函數由結構響應計算值和實測之間的殘差構成。由于結構響應與設計參數之間為隱函數關系，在修正過程中需不斷調用有限元模型來評估目標函數；若有限元模型復雜、單元數量多，這一過程會非常耗時。因此，利用代理模型顯式地表達結構響應和設計參數之間的隱式關系，從而替代有限元模型進行目標函數評估，能夠顯著提高模型修正的效率。

常用的代理模型包括多項式響應面［3］、Kriging模型［4］、徑向基函數［5］、支持向量回歸［6］等，其中以地質統計學為基礎的Kriging 模型因對所有樣本點的精確插值具有比多項式響應面更高的近似精度［7］，且兼具局部與全局的統計特性，具有一定的代表性。Kriging 模型是一種方差估計最小的無偏估計模型，能夠在給出未知函數的預測值的同時給出相應的誤差。胡俊亮等［8］以頻率和模態置信準則（MAC，modal assurance criterion）為修正目標，結合Kriging 模型對一大跨度鋼管混凝土連續梁拱結構模型進行了修正；Khodaparast 等［9］利用Kriging 模型進行了區間模型修正；Liu 等［10］利用試驗模態參數構建目標函數，結合Kriging 模型對一復雜結構進行了模型修正。以上研究在構建Kriging 模型時均采用一次性構建方法，即利用試驗設計，一次性生成所有樣本點。這種方法有2個缺點：1）樣本點數量確定完全憑借分析者的經驗；傳統試驗設計方法如中心復合設計，其樣本點數量是由參數的維度確定的，但由于其樣本點位置有重復，并不適用于模型修正這一類確定性的計算機試驗；現代試驗設計方法如拉丁超立方設計（LHD，latin hypercube design），其基本思想是均勻隨機抽樣，樣本點的數量與參數的個數無關；而標準Kriging 模型樣本點的數量是根據分析者經驗確定的；樣本點數量過大時，不僅導致計算工作量增大，而且會導致過擬合問題；若樣本點數量過小，可能導致精度不足。2）在樣本點數量合適的前提下，由于其空間位置的隨機性，標準Kriging 模型即便通過均方根誤差精度檢測，也不能保證對目標函數極值區域的預測精度。本文采用自適應Kriging 模型進行模型修正，基本思路是通過先前少部分樣本點構建的Kriging 模型對目標函數極值分布進行學習，控制后續增加的樣本點分布在目標函數極值附近，使樣本點在設計空間的位置更為合理，從而提高基于Kriging 模型的模型修正精度。

在可靠度評估方面，Chen 等［11］提出一種局部自適應采樣方法，用于自適應地構建Kriging 模型；利用三個測試函數及一個蜂窩狀結構的可靠度優化設計表明，自適應Kriging 模型同時具備精度和效率。在注塑成型優化設計方面，高月華等［12］提出一種同時考慮預測響應值及其不確定性的加點準則，自適應地構建了Kriging 模型，驗證了自適應Kriging 模型的有效性。在橋梁動力可靠度方面，賈布裕等［13］將自適應策略加入到Kriging 模型，并首次建立了動力可靠度極限狀態方程。然而，自適應Kriging 模型在模型修正領域的應用卻相對較少。李永樂等［14］在進行車-線-橋耦合振動分析時，將自適應Kriging 模型用于修正無砟軌道的有限元模型，并對其進行了精度檢驗；楊修銘等［15］利用頻響函數構建目標函數，結合自適應Kriging模型進行了模型修正。在上述研究的基礎上，本文利用自適應Kriging 模型進行橋梁結構模型修正，通過CCD 估算初始樣本點的數量，然后利用EI 準則和收斂準則控制新增樣本點的位置和數量。同時，結合一座人行斜拉橋，分別利用標準Kriging模型和自適應Kriging 模型構建人行橋的代理模型，并基于環境振動試驗獲得的頻率和振型，對該橋進行了有限元模型修正，驗證了自適應Kriging 模型在實際工程應用中的可行性和優勢。

1 理論基礎

1.1 模型修正理論

有限元模型修正是通過修正結構設計參數，不斷減小結構響應計算值和實測值之間的差異。模型修正是一個優化問題，其目標函數J(x)為

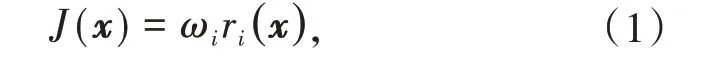
式中x表示待修正參數組成的向量，修正參數包括彈性模量、邊界條件、材料容重、截面慣性矩等；ri(x)表示第i個響應計算值與實測值的殘差函數；ωi為ri(x)的權重系數；nr表示模型修正中考慮的響應類型數量。常用于結構模型修正的響應類型包括靜力位移、應變、頻率、模態振型等。以位移為例，其殘差函數rd(x)可表示為

1.2 Kriging模型

為了避免在修正過程調用復雜的有限元模型，需要將結構響應和修正參數之間的隱函數關系擬合成顯函數。利用試驗設計獲得待修正參數和結構響應的樣本后，可以進一步擬合結構響應關于修正參數的Kriging 模型。Kriging 模型由兩部分組成：線性回歸和非參數部分。即

式中y?(x)表示結構響應的Kriging 模型預估值；f(β，x)為多項式函數，用于模擬樣本點的總體趨勢；β為多項式回歸系數矩陣；z(x)為一隨機過程，服從均值為0、方差為σ2的正態分布，用于模擬樣本點局部近似。由于z(x)的存在，Kriging 模型更適合于近似具有復雜非線性的結構輸入、輸出模型。Kriging 模型常用的精度測試指標如R2、均方根誤差RMSE 等［4］，關于Kriging 模型完整的理論推導過程可參考文獻［16］。

2 自適應Kriging模型

2.1 試驗設計及樣本點數量確定

為了獲取結構響應和待修正參數的樣本，首先需要通過試驗設計獲得待修正參數在設計空間內的樣本，然后結合有限元模型計算結構響應。目前，試驗設計方法可分為傳統試驗設計方法，和現代試驗設計方法兩類。傳統試驗設計方法適用于物理試驗，其特點是樣本點位置相同，但試驗結果仍有可能不同。現代試驗設計方法主要采用了空間填充的思想，其樣本點數量不固定且位置不重合，更適合于計算機試驗。本文選用拉丁超立方設計用于生成修正參數樣本點。LHD 是一種多維分層抽樣試驗設計方法，其樣本點H(i)j為

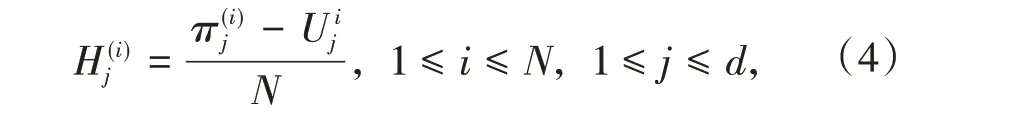
式中π為1到N的獨立隨機排列數；U為在［0，1］之間獨立于π的隨機數；下標j為修正參數的維數，上標i為修正參數的水平數。

對于LHD 樣本點數量的確定，自適應Kriging模型首先需要確定一個初始樣本集，然后根據最大期望準則控制后續新增加點的數量。韓忠華［17］曾指出，自適應Kriging 初始樣本集數量的選擇，并不受設計空間維度的限制，只需滿足代理模型精度要求即可；可見，目前并無明確的方法確定現代試驗設計方法及Kriging 模型的樣本點數量。為此，本文采用CCD 來估算自適應Kriging 模型的初始樣本集數量；并結合收斂準則自適應地控制新增樣本點數量，即樣本點總數由算法自身確定。為了保證可比性，標準Kriging 模型的樣本點總數與自適應Kriging模型相等。

2.2 自適應加點準則

自適應Kriging 模型是通過初始樣本集獲取目標函數在設計空間的分布狀況，使得后續新增的樣本點位于目標函數極值處或預測誤差較大的位置，不斷提升Kriging 模型的精度；當達到一定的條件時，新增樣本點的過程終止，Kriging 模型構建完畢。本文通過初始樣本集得到Kriging 模型對未知點x的預測值和預測標準差后，根據最大期望改善（EI，expected improvement）準則，將EI 函數值作為評價指標，來代表設計空間內任意點對當前樣本集中的最優值的改善程度I(x)，選擇使EI函數值最大點所對應的樣本點作為最佳樣本點，將該樣本點添加到最初的樣本集中更新Kriging 模型，如此循環迭代直至收斂。假設當前樣本集內最優值為ymin，Kriging 模型對未知點的預測值y?服從均值為-y、方差為s2(x)的正態分布。I(x)定義為

函數I(x)的期望（即EI函數）可表示為

式中Φ和ψ分別代表標準正態累積分布函數和標準正態分布概率密度函數。通過優化算法尋找到EI函數值最大點所對應的樣本點作為更新點添加到樣本空間中，不斷更新模型，使得Kriging 模型根據不同的工程實際問題的特性來自適應地選擇樣本點；其收斂準則為

即當最大EI 值與當前最優響應值yopt小于收斂閾值σ時，不再新增加樣本點；σ可根據問題的精度需求確定；若取為1× 10-3，則表示新增樣本點后的最大EI 值與當前最優值之比＜1× 10-3，此精度水平對結構模型修正而言已經足夠。

2.3 基于自適應Kriging模型的模型修正流程

基于自適應Kriging模型的模型修正流程為：

1）根據設計圖紙建立結構有限元模型，基于工程經驗和敏感性分析選擇待修正參數；同時，完成實際結構測試，并建立目標函數；

2）根據修正參數的個數，結合CCD 確定初始樣本點數量；利用LHD 生成初始樣本點，并結合初始有限元模型計算樣本點對應的結構響應；

3）利用初始樣本集構建Kriging 模型，以標準遺傳算法（GA，genetic algorithm）［18］進行迭代，尋找在當前模型基礎上使EI 函數值最大的樣本點作為新增樣本點；

4）結合有限元模型計算新增樣本點對應的結構響應，并用于更新Kriging模型；

5）重復第3～4步，直至滿足式（7）中的收斂要求；

6）對構建的Kriging 模型進行精度測試；若滿足精度要求，進入第7 步；若不滿足，重復3～5步；

7）利用優化算法尋找目標函數在設計空間內的極值；目標函數中的響應計算值由構建好的Kriging模型提供，實測值由試驗數據提供；

8）評估模型修正效果。

3 測試函數

為了測試自適應Kriging 模型相對于標準Kriging 模型的精度，本文選取了六背駝峰函數以及Goldstein-Price（GP）函數作為測試函數。六駝峰函數為

式中F（x）表示測試函數的函數值；x表示自變量；對六駝峰函數，-2 ≤x1≤2，-1 ≤x2≤1；在（0.089 8，-0.712 6）和（-0.089 8，0.712 6）有相同的全局最小值為-1.031 6；對GP 函數，-1 ≤x1，2≤1；在（0，-1）處有全局最小值0.477 12。

采用LHD 構建初始的樣本點，在構建的初始Kriging模型的基礎上，利用GA對EI函數進行尋優來更新模型直到滿足收斂條件為止。GA 參數設置為種群數目為500，迭代次數為200，交叉幾率為0.9，變異幾率為0.1。

根據Matlab 中的命令ccdesign，對CCD，當問題維度為2時樣本點數量為16。因此自適應Kriging模型的初始樣本點數量取為16；由于測試函數有明確的函數形式，計算精度較高，因此自適應Kriging 模型的收斂閾值σ取為1× 10-6；最終，六駝峰函數和GP 函數在初始樣本點的基礎上，分別新增加了28 和33 個樣本點，即總樣本點數量分別為44 和49。對于標準Kriging 模型，則保持總樣本點數量與自適應Kriging 模型相同，利用LHD 一次性抽取44 和49 個樣本點；圖1 和圖2 分別給出了兩個測試函數的標準Kriging 樣本點和自適應Kriging 樣本點，可以看到，通過自適應地添加樣本點的方式，兩個測試函數新增加的樣本點主要位于邊界和函數極值附近。

對構建好的兩種Kriging 模型，采用標準粒子群優化算法（PSO，particle swarm optimization）［19］尋找測試函數在定義域內的最小值，PSO參數為種群數目為30，最大迭代次數為100，速度慣性取0.729，學習因子為2。為獲得統計上有意義的比較結果，避免算法的不確定性，對每個測試函數進行了200 次獨立運算。表1 給出了利用不同Kriging 模型的精度評價和PSO 優化結果。從表1 可看出：（1）在樣本點總數相等的前提下，對兩個測試函數，構建的標準Kriging 模型和自適應Kriging模型的R2均大于0.97；RMSE 最大不超過0.039 3；表明標準Kriging 模型和自適應Kriging 模型均具備較高的精度；（2）進一步地，利用PSO 去尋找兩個函數的最小值，并進行200次獨立計算，分析計算結果的均值和標準差；對六駝峰函數，標準Kriging 模型和自適應Kriging 模型的均值較為接近，且均接近于理論解，但自適應Kriging 模型的結果精度和穩定性更高；對GP 函數，Kriging 模型的均值為0.47，偏離理論解較多；而自適應Kriging 模型的均值為0.84，接近理論解。這主要是因為標準Kriging 模型一次生成的樣本點具有一定的隨機性。從圖2 可看出，在函數極值（0，-1）附近區域點數較少，導致無法準確預測目標函數極值；而自適應Kriging 模型則較好地避免了這個問題。測試函數結果表明，自適應Kriging 能夠避免樣本點在空間分布的隨機性，提高模型對目標函數極值區域的預測精度。

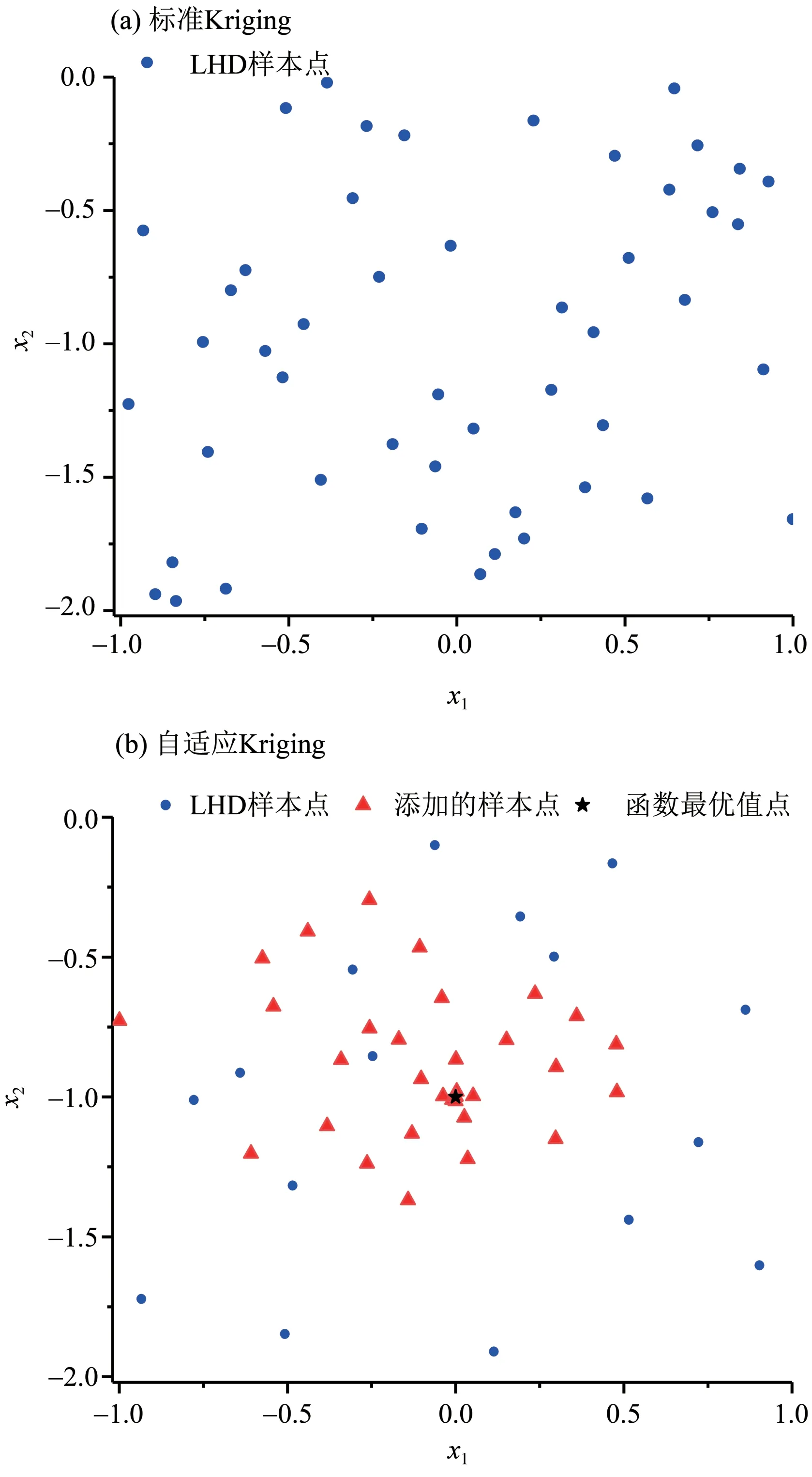
圖2 標準Kriging和自適應Kriging樣本點（GP函數）Fig.2 Standard Kriging sample points and Adaptive Kriging sample points(GP functions)

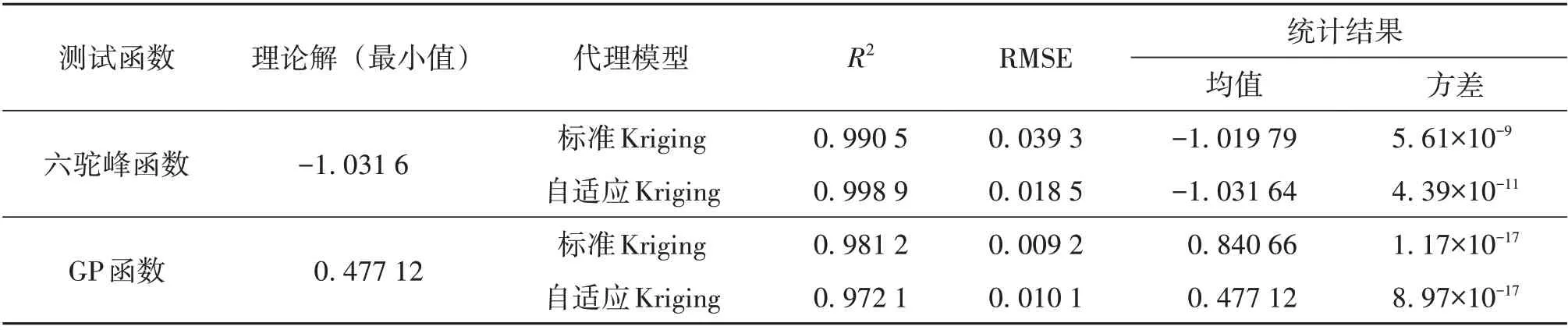
表1 不同Kriging模型的函數值搜索結果Table 1 Function value search results of different Kriging models

4 人行斜拉橋模型修正

4.1 工程概況

理工一橋是一座主跨為45.0 m 的獨塔人行斜拉橋，橋跨布置為（20.0+45.0+21.3）m。主梁為鋼箱梁結構，高0.7 m，如圖3 所示。主梁由直線段和U 型曲線段組成，直線段橋面寬7.0 m，曲線段橋面寬分別為3.5 m 和4.0 m。橋塔采用變截面矩形鋼箱結構，高25.0 m，在橋塔兩側各布置4根拉索。主塔上最高拉索的錨固點距離橋面16.98 m，最低拉索的錨固點為6.48 m，錨固點相互間距為3.50 m。8 根斜拉索中，最長拉索長為34.761 m，最短拉索長為10.618 m，采用主塔端固定和主梁端張拉。根據設計圖紙，基于ANSYS 軟件建立了理工一橋的初始有限元模型（圖4）。主梁及主塔采用Shell63單元模擬，其彈性模量為210 GPa，質量密度為7 900 kg/m3；斜拉索采用Link10 單元模擬，其材料彈性模擬為202 GPa，質量密度7 900 kg/m3。邊界條件按照圖紙設置，主梁與主塔采取固結方式，邊墩處設置兩個板式橡膠支座。

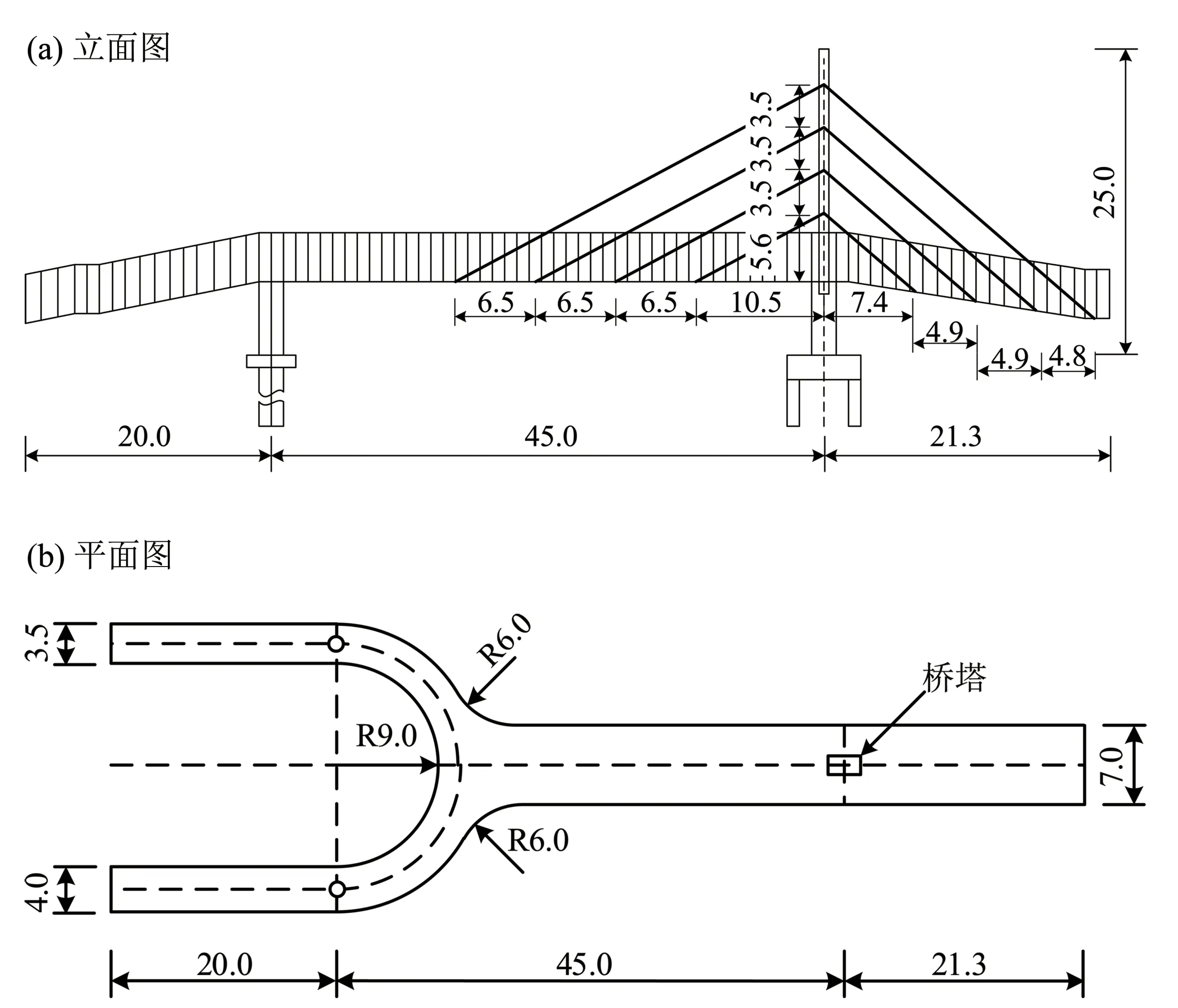
圖3 理工一橋立面圖及平面圖（單位：m）Fig.3 The elevation and plan view of Ligong First Bridge(unit:m)

圖4 理工一橋ANSYS有限元模型Fig.4 The ANSYS finite element model of Ligong First Bridge

4.2 環境振動試驗

為了獲得理工一橋的模態參數，對其進行環境振動試驗。環境振動試驗利用5個無線加速度傳感器，測試橋面在環境荷載下的豎向和橫向加速度，并結合協方差驅動的隨機子空間識別算法識別橋梁的頻率和振型。在橋面兩側平均每隔3 m 布置1個測點，共計布置了53個測點，其中2個為參考點，其余測點通過移動傳感器分17 個測試組完成；每個測試組采樣時間約為15 min，采樣頻率為200 Hz。表2 對比了試驗識別的前4 階頻率的計算值和試驗值，并給出了振型的MAC值；可以看出，前4 階模態振型試驗值與計算值的MAC 值均大于0.93，表明振型識別結果較好。頻率方面，試驗值和計算值的相對誤差均未超過10%，最大相對誤差為7.02%，表明初始有限元模型與實際結構吻合較好，但頻率計算值仍有修正空間。

表2 頻率和振型實測值與計算值Table 2 The frequencies and mode shapes of experimental identified and analytical values

4.3 修正參數與目標函數

修正參數的選擇上，一方面考慮到理工一橋主梁、主塔為鋼箱梁，其截面制造精度較高，因此截面慣性矩未作為修正參數；另一方面，初始模型建立過程中忽略了一些局部加勁肋、焊縫和螺栓，這些會影響到結構的剛度和質量分布，因此修正參數的選擇范圍主要是結構的彈性模量、質量密度；此外，由于斜拉橋的索力對結構響應影響較大，因此斜拉索的初始張拉力也納入修正參數的選擇范圍。在上述思路下，首先選了13 個結構設計參數作為待修正參數，然后進行參數的頻率和模態振型靈敏度分析，選擇靈敏度高的參數作為最終的修正參數。這13 個待修正參數分別是：主塔、T 型橋墩、主跨箱梁、邊跨箱梁、圓弧段箱梁和斜拉索的彈性模量（用E1-E6 表示）和質量密度（用P1-P6 表示）；斜拉索的初始拉應變（用stra 表示）。除了E6的設計值為202 GPa 外，其余構件的彈性模量設計值均為210 GPa；所有質量密度的設計值均為7 900 kg/m3；斜拉索的初始拉應變為7.47×10-3。

對上述13 個待修正參數進行頻率靈敏度和振型靈敏度計算，計算結果如圖5 所示。可以看出，主跨箱型梁的彈性模量E3 和其質量密度P3、圓弧曲線端箱梁的彈性模量E5和其質量密度P5對理工一橋的模態頻率fi敏感性相對較高；主跨箱型梁質量密度P3和圓弧曲線端箱梁的質量密度P5對理工一橋的模態振型敏感性相對較高。綜合考慮，選擇E3、E4、E5、P3 和P5 五個設計數作為修正參數進行模型修正。按照式（1），目標函數由前4階頻率和模態振型的MAC 構建。為保證修正后的參數物理意義，修正過程中各參數的上下界分別為其初始值的1.25和0.75倍。

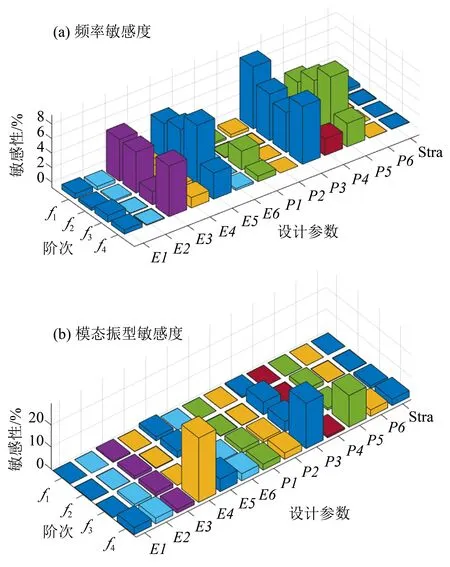
圖5 設計參數敏感度分析Fig.5 The sensitivity analysis of design parameters

4.4 自適應Kriging模型

對于5參數問題，CCD的樣本點數量為46，因此自適應Kriging 模型的初始樣本點數量為46。利用LHD 獲得初始樣本點的空間分布后，結合有限元模型計算樣本點對應的頻率和振型；后續新增樣本點則由EI 準則控制，收斂閾值取為0.01。最終，共計新增了28 個樣本點，即總樣本點的數量為74。為保持樣本點總數一致，Kriging 模型的樣本點數量取為74。以一階頻率關于修正參數E3 和E5 的函數關系為例，標準Kriging 和自適應Kriging擬合的Kriging 響應面分別如圖6 所示。可以看出，標準Kriging 模型的樣本點基本上隨機地布滿設計空間；自適應Kriging 模型的初始樣本點也是隨機布滿空間，但新增的樣本點則一部分集中于邊界，另一部分位于E3［0.7， 0.9］的區間內；這表明自適應Kriging 模型的新增樣本點更具有指向性，即更多分布于RMSE 較大的位置和函數極值區域。表3 給出了標準Kriging 模型和自適應Kriging 模型的R2和RMSE，以評價二者的精度。可以看出，兩個模型的前四階頻率的R2＞0.99，RMSE 值均小于1.07×10-3；除第四階振型外，前三階的振型的R2均大于0.97；RMSE 均小于0.54×10-3；表明標準Kriging和自適應Kriging模型的擬合精度較高。

圖6 標準Kriging和自適應Kriging擬合的一階頻率響應面Fig.6 The 1st order frequency response sufarce fitted by standard Kriging and Adaptive Kriging

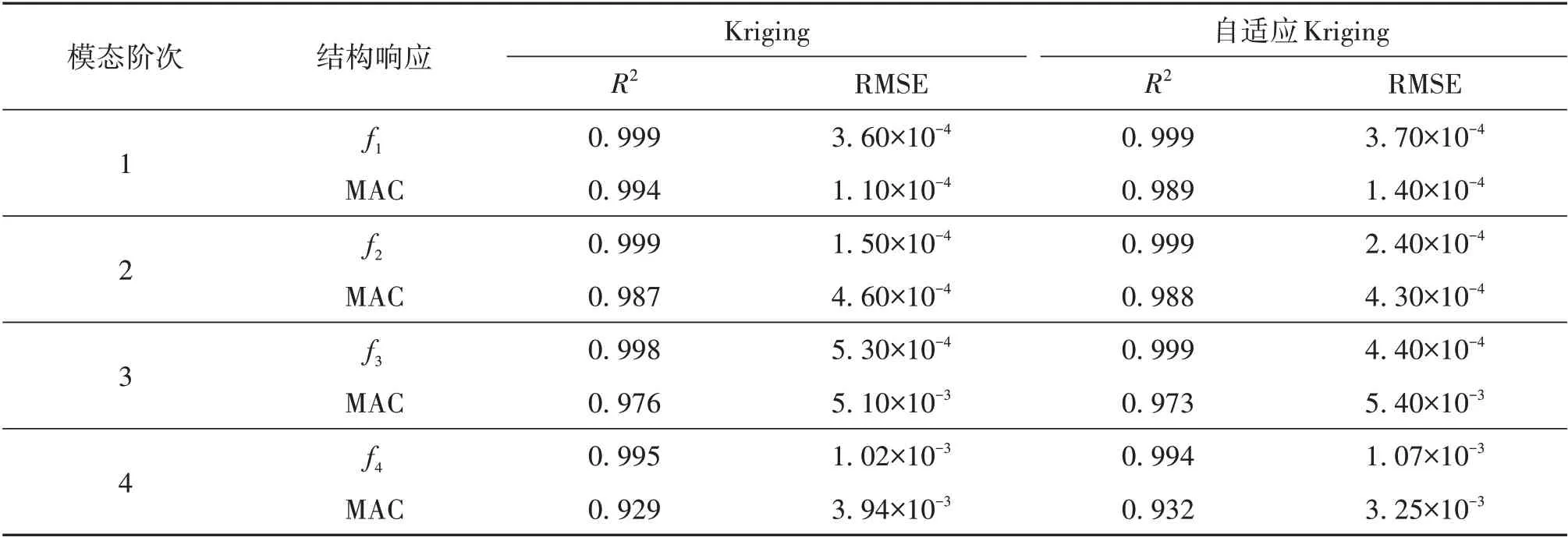
表3 Kriging模型和自適應Kriging模型的精度Table 3 The accuracy of Kriging and Adaptive Kriging model

4.5 結果分析

采用PSO 算法在設計空間內搜索目標函數的最小值；其中，目標函數的計算值分別由標準Krigin 和自適應Kriging 模型預測，試驗值根據實測結果確定。PSO 算法的種群數量取為30，最大迭代次數取100，速度慣性取0.729，社會和認知系數均取為2.0，上述參數均為標準PSO 的默認參數，其合理性已經得到大量工程算例驗證。

表4列出了各修正參數在修正前后的對比，可以看出：（1）除E4 外，兩種模型的修正結果變化趨勢基本一致；（2）自適應Kriging 模型的修正結果中，E3 相比其初始值降低了20.9%，即為其初始值的0.79 倍，這與前述自適應Kriging 新增樣本點的位置是一致的，表明自適應Kriging 通過評估初始樣本集，找到了目標函數極值所在的區域，并對其該區域的樣本點數量進行了增加。需要說明的是，修正參數在修正前后的變化，并非代表材料特性發生了變化，只是表征初始模型和實際結構之間的質量或剛度差異；因此可以理解為等效彈性模量或等效密度；類似的修正幅度在現有文獻中也有描述，如文獻［20］對一座斜拉橋的模型修正，主梁的密度修正幅度達到17.9%。

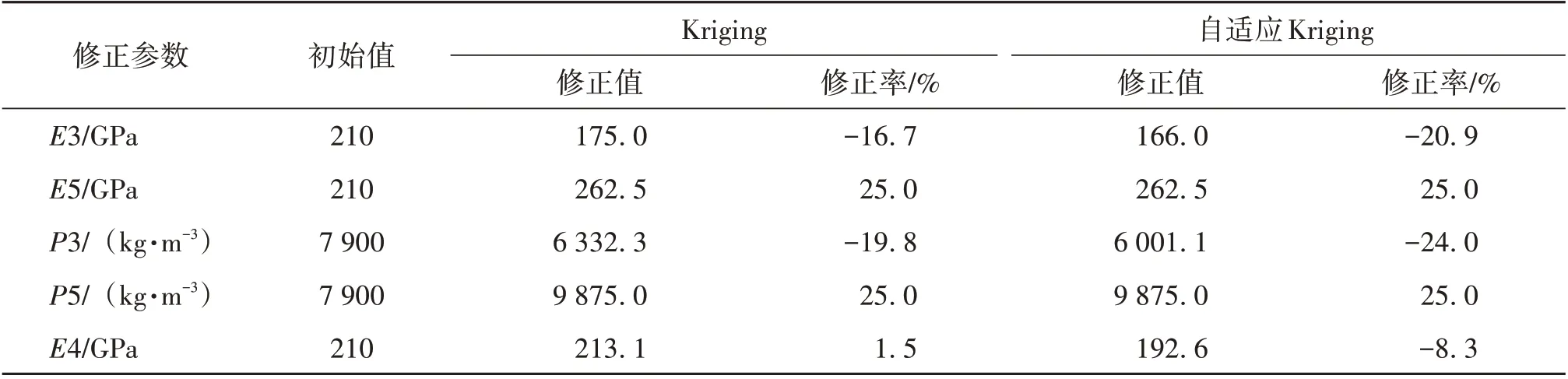
表4 模型修正前后的修正參數值Table 4 The updating parameters before and after model updating

表5 給出了修正前后的頻率和MAC 與試驗值的對比，可以看出：（1）經過模型修正，相比初始模型，兩種Kriging 模型的修正結果均與試驗值更為接近；例如第一階頻率相對誤差由修正前的7.02%降低到修正后的3.08%和2.81%；其余各階頻率精度均有不同程度的提升；相比修正前，修正后的MAC 也有小幅提升；（2）相比標準Kriging 模型，自適應Kriging 模型獲得了更好的修正精度。上述修正結果表明，在樣本點數量一致的前提下，自適應Kriging 模型能獲得比Kriging 模型更好的修正精度。圖7給出了前四階實測振型和自適應Kriging 修正后的模型計算振型對比圖，可以看出，經過模型修正，各振型與實測振型吻合良好。

圖7 模態振型試驗值和自適應Kriging修正值Fig.7 The mode shapes of experimental values and updated values obtained from Adaptive Kriging

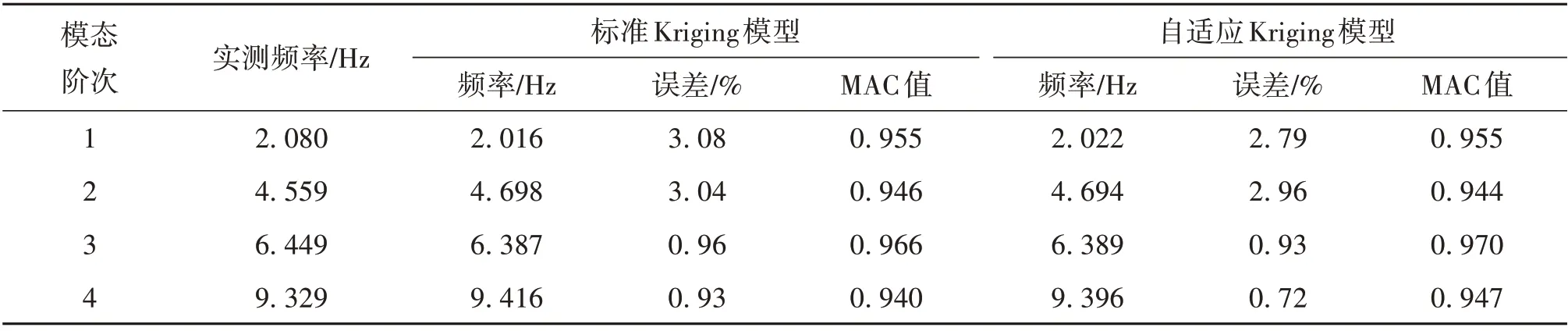
表5 修正結果對比Table 5 The comparison of the updating results

5 結 語

本文構建了一種基于自適應Kriging 模型的有限元模型修正方法，并且提出了一種樣本點總數的確定方法。與標準Kriging 模型一次性生成所有樣本點不同，該方法首先通過CCD 估算初始樣本集的數量，利用LHD 生成樣本點的空間位置，并初步構建Kriging 模型；然后利用EI 準則自適應地控制新增樣本點的位置，直至滿足收斂準則。通過測試函數和理工一橋模型修正對比了標準Kriging 模型、自適應Kriging 模型精度以及修正結果，可得到如下結論：

1）測試函數表明：在樣本點總數一致的情況下，通過計算R2和RMSE，可知自適應Kriging 模型和標準Kriging 模型具有相近的預測精度；但由于自適應Kriging 模型中后續增加的樣本點多位于目標函數極值附近，因此在函數極值附近，自適應Kriging 能夠提供比標準Kriging 更高預測精度；此外，GP 測試函數還表明，即便Kriging 模型通過R2和RMSE 精度測試，由于樣本點分布的隨機性，Kriging 模型對函數極值區域預測精度可能不足，從而導致后續優化結果不正確。

2）理工一橋模型修正案例表明：通過CCD 初步估算樣本點數量，并結合收斂準則控制新增樣本點數量，確定的樣本點總數基本合理。在樣本點總數一致的情況下，自適應Kriging 模型和標準Kriging 模型的精度基本相仿，但自適應Kriging 模型能夠避免樣本點空間分布的隨機性，提高對目標函數極值區域的預測精度，從而獲得更好修正結果。