露天礦運輸系統三維風險評價模型及其量化研究

李雯靜，邱 莉，姚 囝，任大軍

(1.武漢科技大學資源與環境工程學院，湖北 武漢 430081；2.冶金礦產資源高效利用與造塊湖北省重點實驗室，湖北 武漢 430081)

露天采礦包括礦物的開采、運輸和加工，露天礦運輸作業是礦山性能的一個重要特征[1]。 露天礦生產中發生較大運輸事故會嚴重影響露天礦的安全生產，因此，全面客觀準確地對露天礦運輸系統進行風險評價，對降低運輸成本、保證運輸安全具有重要意義。

關于露天礦運輸系統風險評價的研究，袁艷斌等[2]基于熵權法對露天礦運輸系統可靠性進行評價；姜立春等[3]基于W-R-SHEL識別露天礦運輸系統風險因素并采用三級標度(IAHP)與模糊相結合的方法對其進行綜合評判；張彩杰[4]基于PSO-BP神經網絡對露天礦運輸系統進行風險評估；陽富強等[5]基于群決策的改進層次分析法對露天礦運輸系統進行風險評價。上述研究均考慮了風險指標對露天礦運輸系統風險的影響但未考慮風險其他屬性，對風險指標直接進行評判打分卻未對專家評價數據進行分析。由風險發生的可能性(L)和風險后果的嚴重性(C)建立的二維風險模型可對風險進行定性和定量分析，該方法稱為風險矩陣法。但由于風險特征的多維性，許多國內外學者在二維風險模型的基礎上融入風險因素重要度[6-7]、敏感性[8]、脆弱性[9]、可預測度[10]提出三維風險模型。露天礦在運輸過程中發生事故潛在因素與風險的時間價值(E)有關，風險的時間價值(E)即為風險潛在事件發生的頻率對露天礦運輸系統安全評價具有很大的影響，但現有關于露天礦運輸系統風險評價的研究還未考慮這一影響。

鑒于此，本文首次在露天礦運輸系統風險評價中采用風險矩陣法，在二維風險模型的基礎上，考慮風險的時間價值建立露天礦運輸系統三維風險模型。為了解決三維風險模型難以量化的問題，結合風險因素各等級的量化值提出改進的雷達圖法，實現自適應劃分三維風險評價結果等級區間；融入指標相關性改進的結構熵權法，使其全面客觀計算露天礦運輸系統指標權重；結合未確知有理數、模糊集理論改進傳統模糊物元，實現客觀準確識別專家支持、反對和中立評價信息并量化風險因素E、L、C的評價結果。

1 露天礦運輸系統三維風險模型

1.1 三維風險評價模型

露天礦在運輸工作中發生的潛在事件與特征時間框架有關，存在具有較高風險水平的事件而發生頻率較低，其處理浪費了更多的預算和時間，也存在具有較低風險水平的事件而發生的頻率較高，未對其及時采取管控措施會造成嚴重的傷亡，故應強調將影響露天礦運輸系統安全的潛在事件的時間價值作為有效參數?；诖耍疚脑诙S風險模型的基礎上增加了一個表示風險時間價值的新維度建立露天礦運輸系統三維風險評價模型。

參考露天礦安全相關研究文獻[11]，將露天礦運輸系統風險的時間價值E、風險發生可能性L和風險后果的嚴重性C劃分為五個等級，定性、定量描述見表1。

表1 露天礦運輸系統三維風險模型參數描述Table 1 Description of 3D risk model parameters ofopen-pit mine transportation system

露天礦運輸系統三維風險評價模型以E(以1、2、3、6、10依次表示風險時間價值即風險發生的頻率的高低)、L(以0.5、1、3、6、10依次表示事件發生的可能性大小)及C(以1、2、5、10、20依次表示事件發生嚴重程度)3個維度考慮風險指標的相對動態性，該模型很好地彌補了二維風險模型在風險時間價值方面的不足，將風險水平恒定的二維風險模型變成動態的三維風險模型。

1.2 基于改進雷達圖法自適應劃分三維風險評價結果等級區間

雷達圖法將待評價對象的評價指標狀況用二維平面圖形表示，是典型的圖形評價方法[12]。郭榮昌等[10]提出了改進的雷達圖法來構建三維風險矩陣，該方法簡單采用各等級比值求取扇形面積但未考慮各風險因素各等級具有不同量化值，因此，本文基于該方法，考慮各風險因素各等級的量化值改進雷達圖法。此外，針對三維風險評價結果等級區間難以確定的問題，采用本文提出的方法計算各風險因素量化結果后對其進行數據分析，結合其數據變化特征自適應劃分三維風險評價結果各等級分布區間?；诟倪M雷達圖法自適應劃分三維風險評價結果等級區間具體步驟如下所述。

1) 風險評價等級劃分。在風險評價中需要根據相應的標準來判斷指標的風險是否可被接受，是否需要采取進一步的安全措施。本文根據二拉平原則(ALARP)[13]可將風險等級劃分為可忽略的、容許的、不希望的、不可容忍的4個等級。

2) 風險因素量化原理。用指標軸之間的夾角表示風險因素的權重，用扇形面積來表示該風險因素對風險評估結果的影響。本文設定各風險因素對露天礦運輸系統重要度一樣，用各風險因素各等級的量化值與其最高等級量化值之比作為扇形半徑求取扇形面積，計算見式(1)。

(1)

在風險發生可能性L為可能等級下，畫出不同風險的時間價值E和后果的嚴重性C等級下的雷達圖如圖1所示。其中，第一組為很少等級下的雷達圖，第二組為較少等級下的雷達圖，第三組為偶爾等級下的雷達圖，第四組為頻繁等級下的雷達圖，第五組為持續不斷等級下的雷達圖，圖中用“+”符號填充后果的嚴重性C，用“/”符號填充風險的時間價值E，用“*”填充可能性L。

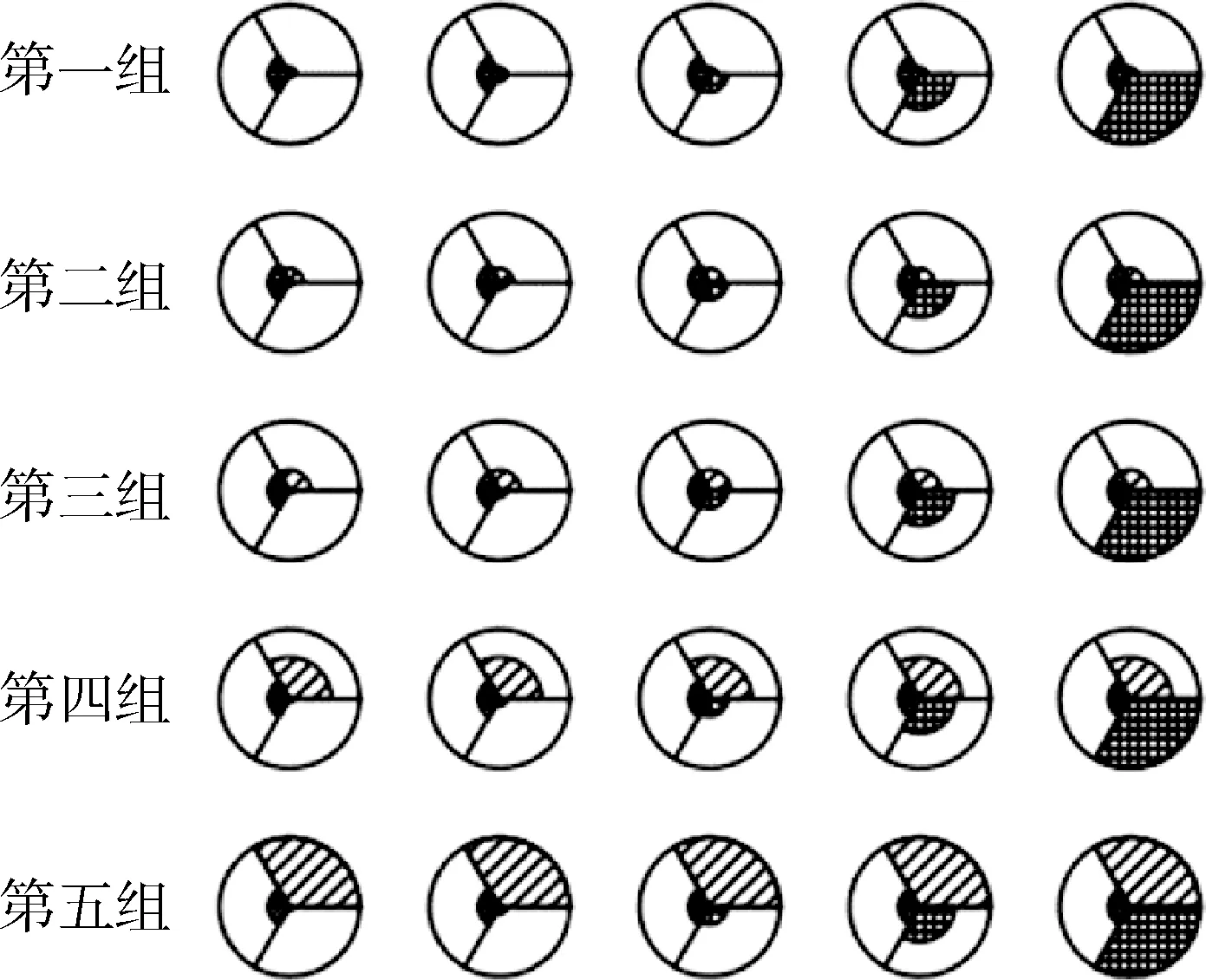
圖1 不同風險因素情況下雷達圖Fig.1 Radar chart under different risk factors

用扇形面積之和與單位圓面積的比率ηELC作為風險評價等級結果，計算見式(2)。

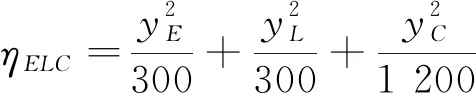
(2)

式中，yE、yL、yC分別為風險因素E、L、C各風險等級的量化值。

3) 風險因素量化結果分析。根據式(2)可以得到共計125個元素對應的風險評價等級結果，將數據按照從小到大的順序排列后進行數據分析，得到曲線圖如圖2所示。

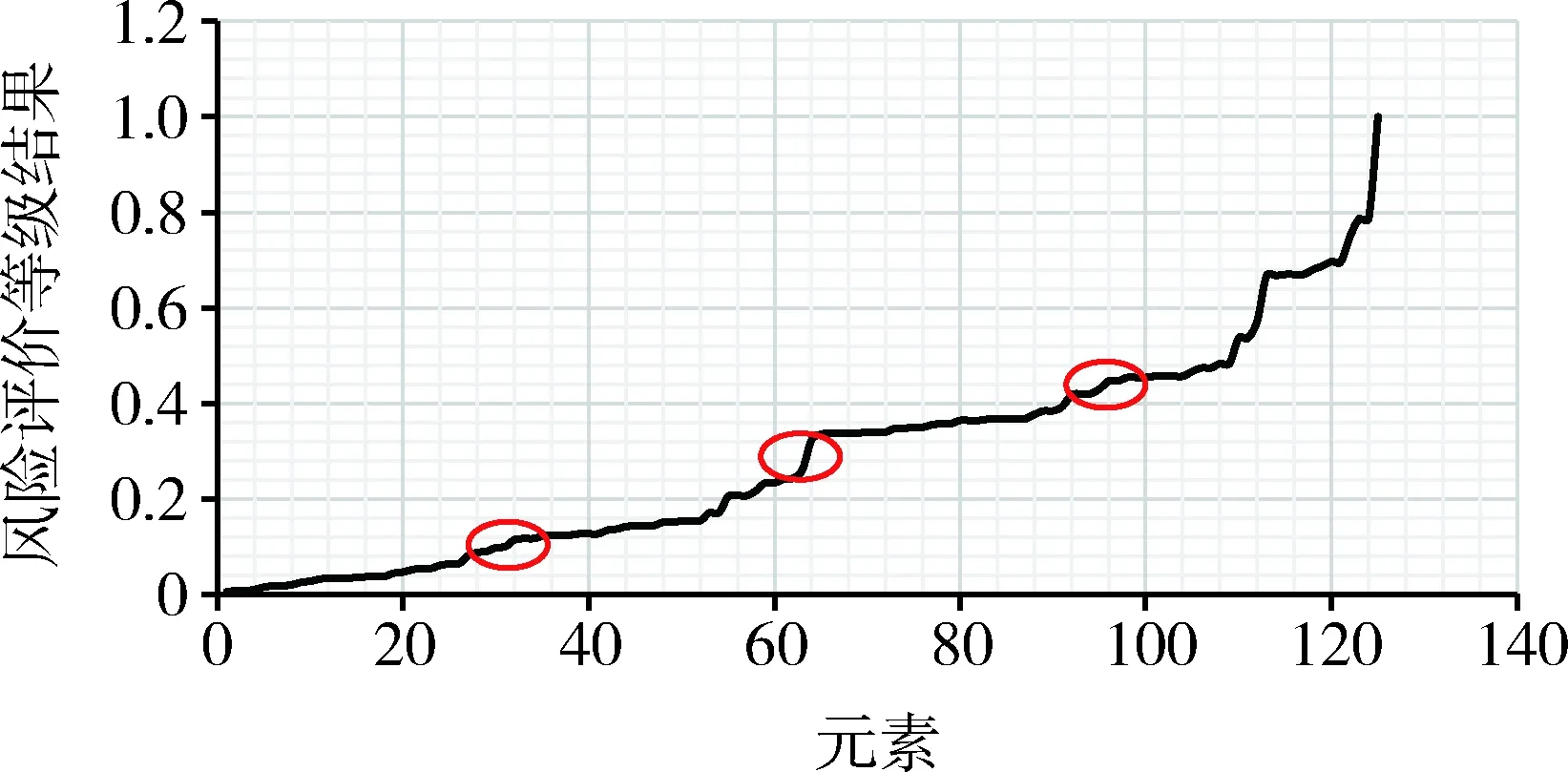
圖2 各風險因素量化結果曲線圖Fig.2 Curve chart of the quantitative results ofeach risk factor

由圖2可知，計算結果大小在[0，1]之間，其中比率越大，表明風險越大，反之越低。圖中3處圓圈標記的區域共同點是數據快速增加之后保持一段區間的穩定，第一個區域中第35個數據增值達到0.121 7之后保持3個點穩定于0.124 2，第二個區域中第65個數據增值達到0.335 0之后保持4個點穩定于0.337 5，第三個區域中第100個數據增值達到0.454 2之后保持4個點穩定于0.456 7。 本文結合風險因素量化結果的數據變化特征將三維風險評價結果的4個等級區間劃分可忽略的[0，0.121 7]、容許的(0.121 7，0.335 0]、不希望的(0.335 0，0.454 2]、不可容忍的(0.454 2，1]。

2 基于改進的結構熵權法的露天礦運輸系統評價指標權重確定

2.1 評價指標體系建立

露天礦運輸事故是由人、機、環、管、物五個子系統相互作用的結果，5個子系統不是獨立存在的個體，而是相互作用、相互聯系的動態系統?；诖耍瑓⒖紡埐式躘4]研究方法從人、機、環、管、物即“5M因素”出發，建立5個一級指標、17個二級指標露天礦運輸系統風險評價指標體系，見表2。

2.2 改進的結構熵權法

為了避免主觀賦權過分依賴專家主觀經驗和客觀賦權可能與事實不符的情況，程啟月[14]基于主觀德爾菲法與客觀熵值法提出“結構熵權法”來確定指標的權重，該方法將客觀和主觀相結合可提高結果的準確性[15-16]。CRITIC法[17]是一種客觀賦權法，它結合指標的信息量和指標間的相關性來分配指標權重，較客觀賦權法中的熵權法具有顯著的優越性[18]。

露天礦運輸系統每個子系統相互聯系、相互依存，反映露天礦運輸系統風險指標之間存在相關性，而結構熵權法中定量計算方法熵權法只考慮了指標之間的信息量而未考慮指標之間的相關性，因而不能適用于風險指標之間存在相關性的露天礦運輸系統風險評估評估中。為此，結合CRITIC法原理改進結構熵權法，在結構熵權法的基礎上融入指標的相關量。

2.2.1 基于德爾菲法經典序列建立評價指標矩陣

向若干熟悉露天礦運輸系統安全風險領域的專家采集指標重要性排序信息，各指標按重要性由高到低排列，如1分代表“最重要”，2分代表“第二重要”等，具體見表3。設有p名專家獨立地對q項指標進行重要性排序，則可以得到經典序列評價指標矩陣見式(3)。

Apq=[Iij](i=1,2,…,p;j=1,2,…,q)

(3)

式中，Iij為第i個專家對第j個指標的排序值。

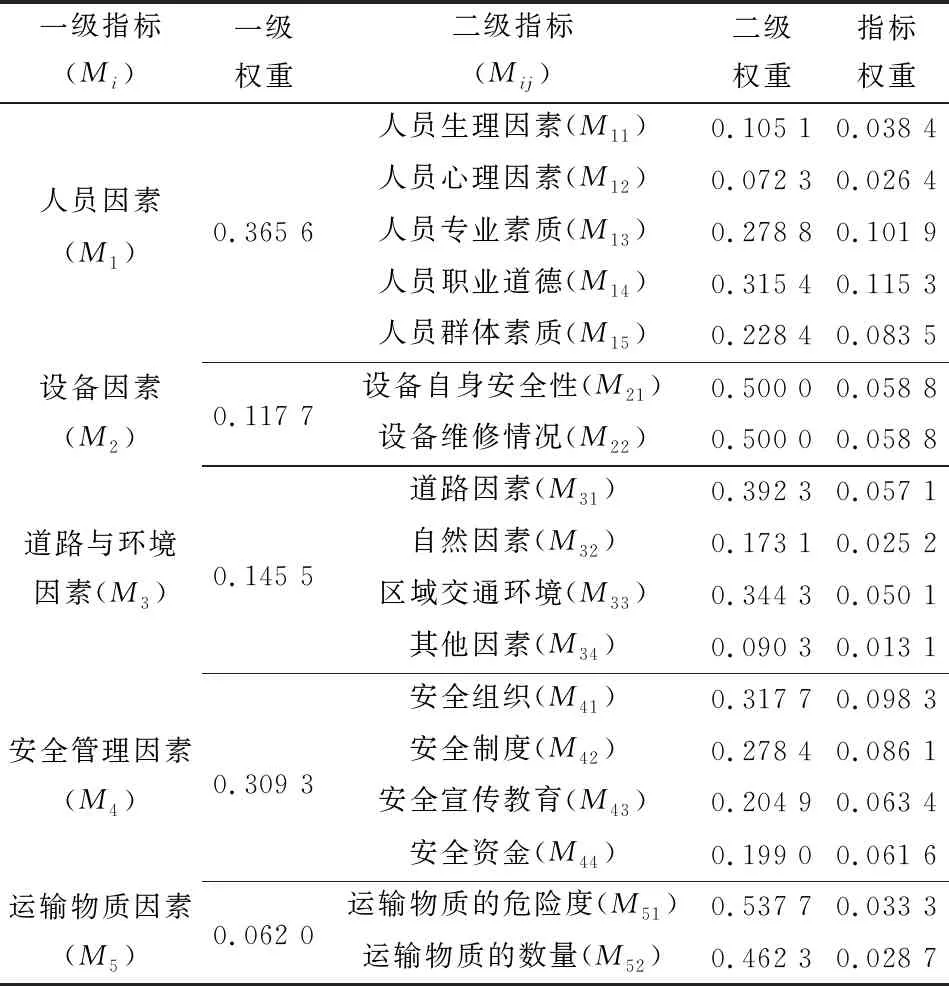
表2 露天礦運輸系統評價指標權重及其權重Table 2 Evaluation index weight and its weight valueof open-pit transportation system

表3 評價指標重要性排序的量化標準Table 3 Quantitative criteria for ranking the importanceof evaluation indexes

2.2.2 指標相關性計算

1) 采用Z-score方法對經典序列評價指標矩陣Apq中各指標值標準化，見式(4)。

(4)

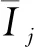
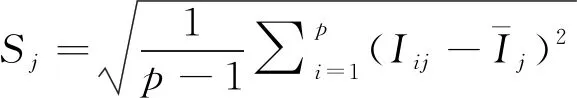
(5)

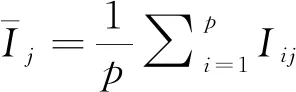
(6)

2) 利用步驟1)得到的標準化矩陣計算各指標間的皮爾遜相關系數，得到相關系數矩陣，見式(7)。

Rqq=[rkj](k=1,2,…,q;j=1,2,…,q)

(7)

式中，rkj為第k個指標與第j個指標的相關系數。

3) 根據相關系數矩陣，可求得各評價指標的獨立性系數Bj,見式(8)。

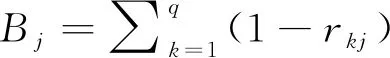
(8)

2.2.3 指標信息量計算

1) 構造結構熵隸屬度矩陣。為了消除經典序列通常含有來自專家意見的“數據噪聲”，減少不確定性，需要對典型排序矩陣Apq進行熵值分析。定義轉換熵函數[19]見式(9)。

(9)

式中，ε為轉換參數量，定義ε=q+2[14]。

將矩陣Apq中各個Iij代入式(9)對進行定量轉化，即可得到結構熵隸屬度矩陣見式(10)

Fpq=[uij](i=1,2,…,p;j=1,2,…,q)

(10)

式中，uij為i個專家對第j個指標的排序值Iij的隸屬度。

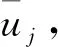
(11)

定義專家i對指標j由認知產生的不確定性稱為“認識盲度”，記作Qj，見式(12)。

Qj=

(12)

對于每一個指標，定義專家關于指標j的總體認識度為Fj,見式(13)。

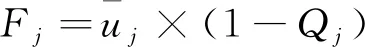
(13)

2.2.4 計算各評估指標的權重

1) 根據各評估指標的獨立性系數和總體認識度，可求得各評估指標的綜合性系數ωj，見式(14)。

ωj=FjBj

(14)

2) 為得到各個指標的權重，需要對Qi進行歸一化處理得到各指標權重wj,見式(15)。

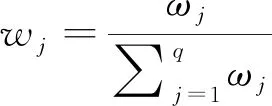
(15)

3 基于改進模糊物元的露天礦運輸系統三維風險評價模型

露天礦運輸系統三維風險評價是一個典型的模糊評價問題，專家評價數據中包括大量不確定信息。為了更好地處理露天礦運輸系統三維風險評價中的不確定信息，針對傳統模糊物元的不足，基于模糊集改進模糊物元，使其可以從支持、反對和中立信息三方面量化專家評價數據?？紤]專家以給定風險指標所處的風險水平的評價方式不能全面提取專家評價信息且具有主觀性、不確定性，基于未確知有理數客觀準確地提取支持、反對和中立信息，實現全面客觀分析專家評價信息。

3.1 基于模糊集與物元理論構造模糊物元

以模糊理論與物元理論發展的模糊物元得到廣泛應用[20-21]，它用事物、特征、模糊特征量值有序三維總體來表示評價對象。由于傳統模糊理論只關注正信息而忽略了負信息和不確定信息，導致傳統的模糊物元不支持從支持、反對和中立三個方面量化專家評價信息。GAU等[22]提出的模糊集理論可以從支持、反對和中立三個不同的觀點中提取信息從而對不確定信息處理有更廣泛的覆蓋?；诖耍谀：碚摳倪M傳統模糊物元，使得重新構造的模糊物元能夠從支持、反對、中立三個方面量化專家評價數據?；谀：c物元理論構造的模糊物元計算，見式(16)和式(17)。

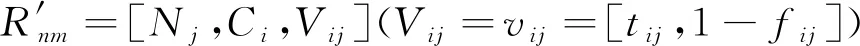
(16)

πij=1-tij-fij

(17)

式中：Nj(j=1,…,m)為事物，指露天礦運輸系統的風險因素E、L、C的風險等級；Ci(i=1,…,n)為事物的特征，指露天礦運輸系統的風險指標；Vij(i=1,…,n;j=1,…,m)為模糊特征量值即隸屬度，是第j個風險等級的第i個風險指標的特征模糊量值；vij為專家支持、反對和中立評價信息；tij為專家評價結果的支持的部分；fij為專家評價結果的反對的部分；πij為專家評價結果的中立部分。

通過改進后模糊物元可將露天礦運輸系統三維風險評價表示為評價等級、評價指標和評價等級特征量值，這種三維方法支持從支持、反對、中立三方面量化專家評價數據。

3.2 基于分布密度型未確知有理數識別中立部分

基于模糊集與物元理論構造模糊物元能夠從支持、反對、中立3個方面量化專家評價數據，但專家對露天礦運輸系統進行評價時，以給定風險指標所處的風險水平的評價方式只能直觀提取出支持數和反對數，這種直觀的方式不能全面提取專家評價信息且具有主觀性、不確定性。如何正確識別出專家評價結果中的中立部分成為客觀準確量化露天礦運輸系統三維風險評價結果的關鍵。而基于未確知有理數理論能從一組數據中識別出“異常”數據[23-24]，基于此，本文引入未確知有理數的可信度概念，構造可信度分布密度函數φ(x)使其能正確識別出專家評價數據中的異常信息，以此客觀準確識別出露天礦運輸系統風險評價數據中的中立部分。

專家評價數據是各風險指標所處的風險等級，基于此根據未確知有理數概念，將專家評價數據定義為未確知有理數D，見式(18)。

D={[Gimin,Gimax],φ(x)}(i=1,2,…,5)

(18)

結合專家評價數據的特點本文將φ(x)定義為式(19)。

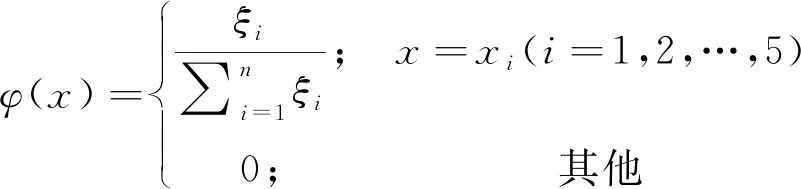
(19)

式中，ξi為每個專家評價的等級i在i等級的可信度距離d內其他專家數量。

基于分布密度型未確知有理數正確判別出露天礦運輸系統風險評價數據中的中立部分需要設定可信度距離d。d的值與評價因素E、L、C的風險等級有關，取各等級相鄰一個等級區間，即對于風險因素L的偶爾等級，它的可信度區間為較少與頻繁之間。根據設定的d值，當每個專家評價等級在該等級可信度距離d內均有其他專家時，代表所有數據具有可信性，則不存在中立部分；當存在某個專家評價等級在該等級可信度距離d內沒有其他專家時，該專家評價數據所對應的ξi為0，則該數據即為中立部分。

3.3 綜合評價

上述構建的模糊物元中模糊特征量值雖能客觀反映專家支持、反對和中立三部分評價結果，但并不能直觀反映露天礦運輸系統三維風險因素E、L、C與其對應的風險等級的接近度。為了實現這個目的，首先將模糊特征量值根據從優隸屬度原則標準化得到待評估模糊物元，并根據從優隸屬度的最大值構建標準模糊物元；然后求取待評估模糊物元與標準模糊物元兩者之間的接近度，構造復合模糊物元；最后根據復合模糊物元與指標權重得到露天礦運輸系統風險因素E、L、C與其評價水平的貼近度。具體步驟如下所述。

(20)

其中，需要采取得分函數對模糊集中的所有特征模糊量值進行排序，通過對Sij進行排序，可以識別出maxvij,得分函數見式(21)。

Sij=tij-fij

(21)

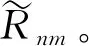
2) 構建標準模糊物元。本文根據各評價指標從優隸屬度的最大值為最優原則，定義了標準模糊物元Rn0。

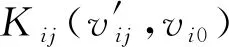
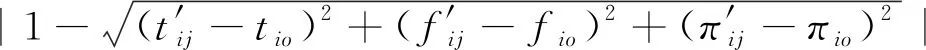
(22)

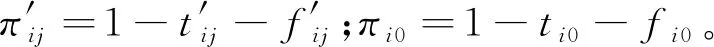
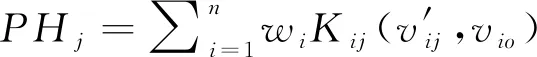
(23)

因此，構建了歐式貼近度模糊物元RPH，實現對露天礦運輸系統三維風險模型定量分析。根據最大貼近度的原則最大PHj(j=1,…,m)值為露天礦運輸系統三維風險因素E、L、C的風險等級，將等級對應的量化值代入式(2)可知三維風險評價結果。

4 實例論證

某露天礦運輸系統上山為皮帶運輸、大巷串車提升，以6名專家對該露天礦運輸系統進行評價，專家評價結果以及處理后最終結果如下所述。

4.1 基于改進結構熵權法計算權重

采用改進結構熵權法確定露天礦運輸系統指標體系中各級評價指標的權重。以一級指標為例，指標權重的確定過程如下所述。

1) 6個專家相互獨立地對5個一級指標進行重要性排序，形成專家意見的典型排序矩陣A65,見式(24)。

2) 根據式(4)～式(8)，得到一級指標的獨立性系數為B5=(0.972 6,0.434 5,0.562 6,0.880 9,0.399 4)。

3) 根據式(9)～式(13)，得到一級指標的信息量為F5=(0.949 7,0.684 5,0.653 5,0.887 3,0.392 6)。

4) 根據式(14)和式(15)，求取一級指標綜合系數后進行歸一化處理，得到一級指標權重為w5=(0.365 5,0.117 7,0.145 5,0.309 3,0.062 0)。

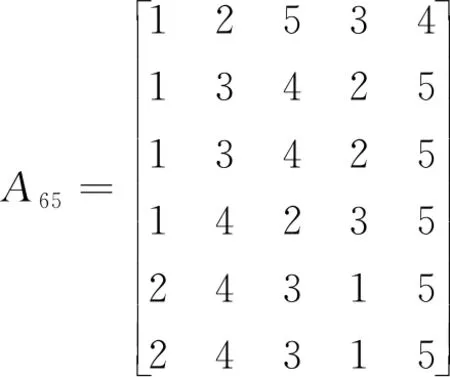
(24)

利用相同的方法，確定各二級指標的權重。最后分別將相對應的兩級權重相乘的結果作為各個指標的權重值(表2)。 由表2可知，致使該露天礦發生運輸事故的人員因素所占比重最大，其次是安全管理因素，這與該露天礦交通事故發生的主要原因相符。

4.2 基于改進模糊物元計算三維風險評價等級

4.2.1 基于分布密度型未確知有理數識別中立部分

專家對該露天礦運輸系統的17個風險指標L、C、E分別做出評價，結果見表4。在指標L中，評價指標M32中支持幾乎不可能、不太可能、可能、很可能、幾乎完全可能等級的專家數量分別為2個、3個、0個、1個、0個，則專家評價等級為幾乎不可能、不太可能、很可能在相應的等級可信區間內其他專家個數分別為4個、4個、0個，故幾乎不可能、不太可能、很可能分別對應的可信度分布密度為1/2、1/2、0，由于可能和幾乎完全可能等級專家支持數據為0故不用進行識別。通過分布密度型未確知有理數判斷出支持很可能等級的可信度分布密度為0，則認為這名專家很可能等級評價數據被視為中立部分。同理可以判斷指標L中存在中立部分有M13、M31、M32、M33、M41、M42、M52，指標C中存在中立部分有M11、M15、M31、M33、M41、M43、M51，指標E中存在中立部分有M21、M33、M42、M44、M52。

4.2.2 綜合評價

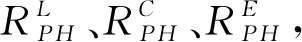
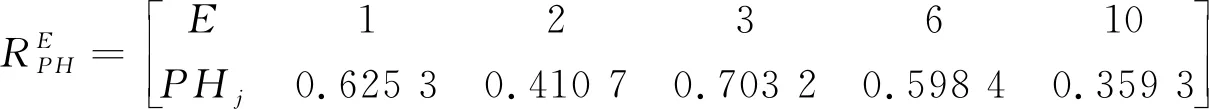
(25)

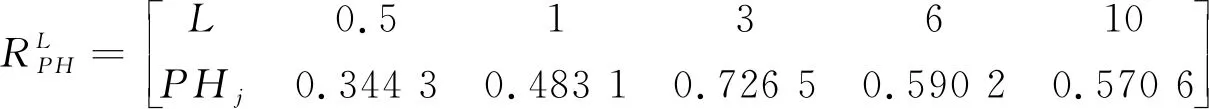
(26)

(27)

表4 專家評價結果Table 4 Expert evaluation results

5 結 論

1) 在二維風險模型基礎上將風險事件價值引入到露天礦運輸系統風險評價中，提出了包含風險發生的可能性(L)、風險后果的嚴重性(C)和風險時間價值(E)的露天礦運輸系統三維風險評價模型。結合風險因素各等級的量化值提出改進的雷達圖法，根據數據變化特征自適應劃分三維風險評價結果各等級分布區間。

2) 結合露天礦運輸系統相互作用、相互聯系的特點，在結構熵權法的基礎上融入指標的相關量，提出改進后的結構熵權法，使其全面客觀計算露天礦運輸系統指標權重。

3) 為了全面客觀分析和處理專家評價數據中包含大量不確定的信息，基于模糊集改進模糊物元，使其支持從支持、反對和中立信息三方面量化專家評價數據，基于未確知有理數客觀準確地提取支持、反對和中立信息。

4) 實例中露天礦運輸中安全風險屬于“容許的”等級，該評價結果與露天礦運輸系統實際情況相吻合，說明本文構建的評價方法具有科學性和實用性。本文中的三維風險評價模型及其量化方法評為露天礦運輸系統的風險評價提供一種新的思路和方法，對露天礦運輸系統的安全管理具有一定的指導意義，同時，也可以應用于其他安全評估領域。