基于面部特征的線上關注度檢測與判斷
吳 迪, 馮曉婉, 宋家豪
(沈陽師范大學 物理科學與技術學院, 沈陽 110034)
0 引 言
受新冠疫情的影響,線上教學[1]已經成為學生的重要補充學習模式之一。同時,隨著信息化和智能化的飛速發展,將信息技術融入教育教學推進“教育+互聯網”[2]已經成為教育教學的新常態。由于線上學習的學生缺乏教師監督和指導,師生互動性降低,學生的線上關注度下降,注意力分散[3]。因此,線上教學需實時檢測學生的關注度。
近年來, 人臉檢測已被廣泛應用于教育教學、刷臉支付、安檢系統等諸多領域。 國內外學者提出了許多人臉檢測方法, 如基于HOG特征的人臉檢測算法[4], ZHANG等[5]提出的MTCNN算法等。 人眼定位的方法包括基于人臉檢測和面部特征點的定位算法[6]、 灰度積分投影的定位算法[7]、 Hough變換的定位算法[8]等。 注意力是學生在線學習[9]、 眼動追蹤[10]、 疲勞駕駛[11-12]等方向的重要研究內容。
綜上所述,本文設計了基于面部特征的線上關注度檢測與判斷方法。首先,采用Dlib庫檢測視頻圖像中的人臉和12個眼部特征點。其次,通過計算2個外眼角所在直線與水平線之間的傾斜角度,進而分析人臉是否正視屏幕,對未正視屏幕的人臉圖像進行矯正。在矯正的人臉圖像上獲取眼部特征點組成的灰度圖,求出虹膜和瞳孔區域,計算瞳孔中心位置。最后,通過瞳孔中心在眼部的位置判斷線上關注度。
1 人臉檢測及眼部特征點定位
本文基于Python程序設計語言、TensorFlow框架、OpenCV和Dlib庫處理獲取的視頻圖像。Dlib庫在正面人臉檢測和面部特征點定位方面,具有較好的效果。其中,dlib.get_frontal_face_detector人臉框位置檢測器和shape_predictor_68_face_landmarks.dat面部68個特征點檢測模型可以獲取人臉位置及面部特征點。圖1和圖2分別為利用Dlib庫檢測人臉位置的效果圖、基于人臉68個特征點模型對眼部12個特征點檢測和定位的效果圖。

2 人臉矯正
在正常狀態下,由于受坐姿的影響,頭部左右偏轉的姿態在較大程度上影響眼部注意力狀態的判斷。因此,首先將實時采集的人臉圖像進行矯正,然后獲取眼部圖像并判斷眼部注意力狀態,可在一定程度上提高眼部注意力狀態的檢測精度。
利用式(1)計算左右眼睛2個外眼角所在直線與水平線之間的傾斜角度:
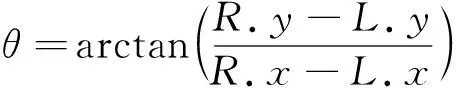
(1)
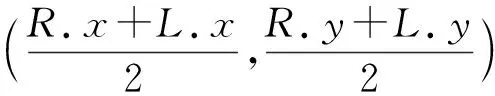

(a) 未矯正的人臉(b) 已矯正的人臉圖3 原圖Fig.3 Original image
3 關注度判斷
3.1 瞳孔中心定位
由圖5可以看出,人臉矯正后,根據眼部特征點的坐標獲取矩形眼部區域,在左右眼二值化圖像中求取面積最大的連通區,即為虹膜和瞳孔區域。由于虹膜與眼睫毛的顏色相近且受上下眼瞼邊緣的影響,導致虹膜區域擴大,從而影響虹膜和瞳孔區域中心位置的確定。

(a) 左右眼矩形眼部區域(b) 左右眼二值化(c) 左右眼虹膜區域
在已矯正的人臉圖像中,如果以人眼的6個特征點為頂點獲取眼部灰度圖像,可減小眼睫毛和眼瞼邊緣對虹膜和瞳孔區域定位的影響。首先將眼部灰度圖像進行濾波、腐蝕、二值化等預處理,然后利用二值化圖像求出虹膜和瞳孔的區域,由于醫學上普遍認為瞳孔位于虹膜中央[13],故將虹膜和瞳孔區域的中心作為瞳孔中心位置,如圖6所示。

(a) 原圖(b) 灰度化(c) 二值化(d) 虹膜和瞳孔區域(e) 瞳孔中心位置
3.2 眼部注意力狀態
眼睛的注視方向可用來判斷注意力是否集中,瞳孔位置是分析眼部注意力狀態的主要因素,通過計算瞳孔中心位于眼部圖像中的位置,可以判斷眼睛向左注視或向右注視,進而確定眼睛是否正視屏幕。在圖7中:
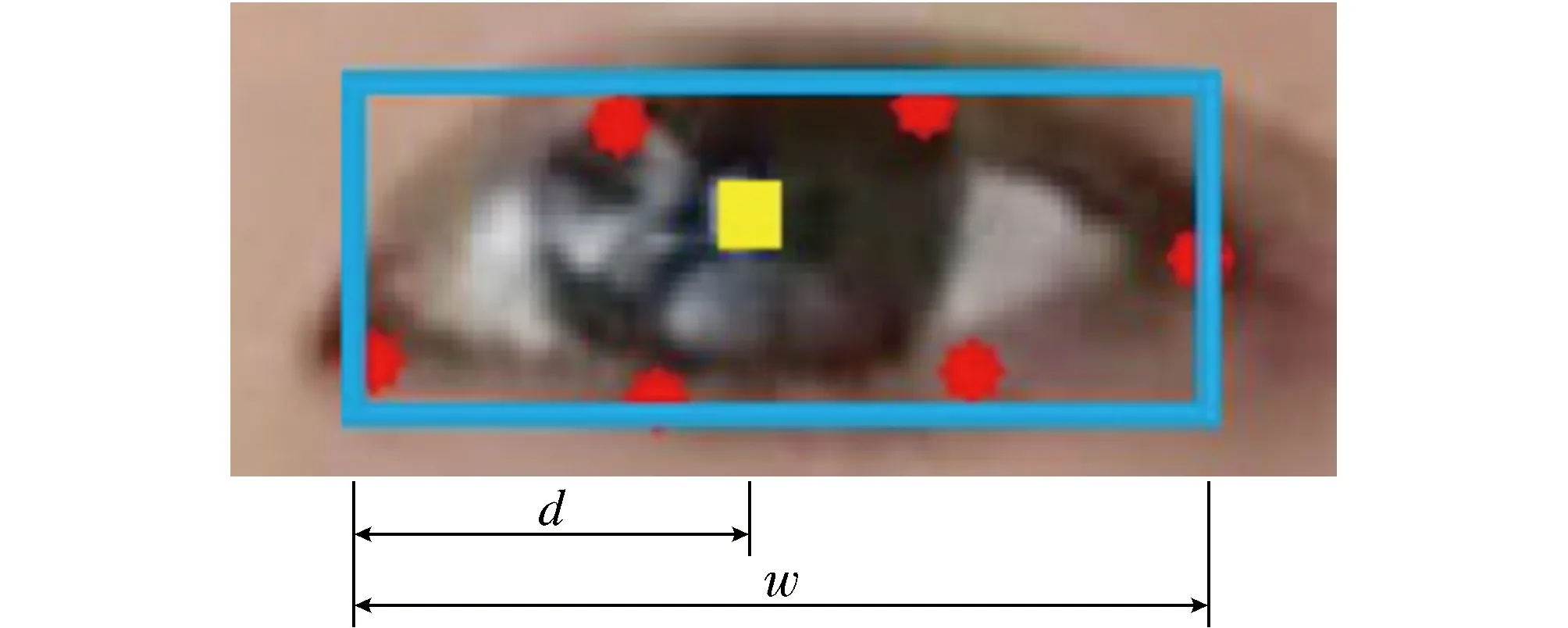
圖7 眼部注意力狀態Fig.7 Attention state of the eye
1) 向左注視:d<0.45×w;
2) 向右注視:d>0.75×w;
3) 正視屏幕: 0.45×w 其中:d為瞳孔中心與圖像左側眼角之間的水平距離;w為內眼角與外眼角之間的水平距離。如果連續3秒以上檢測到眼睛向左(右)注視,則判斷眼睛未正視屏幕,注意力分散。 線上關注度檢測主要對眼部注意力狀態進行分析,即判斷瞳孔中心在眼部圖像中的位置。在BioID數據集中隨機選取面部無任何遮擋的300張人臉圖像并進行測試,其中,274張圖像可以較好判斷出人眼正視屏幕、向右注視和向左注視,圖8展示了部分關注度測試結果。剩余的26張圖像中,由于光照、眼睛縱橫比小于眼睛閉合的臨界閾值[14-15]以及默認閉眼等因素,未能準確地判斷出眼部注意力狀態,部分誤差測試結果如圖9所示。在300張圖像的實驗測試中,準確率約為91.3%。 (a) 正視屏幕(b) 向右注視(c) 向左注視 (a) 瞳孔中心定位誤差(b) 默認閉眼 實驗結果表明,在無任何遮擋的情況下,本文所設計的方法能夠較好地分析眼部注意力狀態,有效地判斷學生線上學習的關注度。由于光照角度和面部遮擋等因素的影響,本文所設計的方法檢測精度降低,在未來的工作中將進一步完善。4 測試結果及結論



