帶兩個不同半徑環(huán)形剛性隔板的圓柱形儲液罐內(nèi)流體晃動特性研究

曹占雪，王佳棟，溫國正

（江蘇大學(xué) 土木工程與力學(xué)學(xué)院，江蘇 鎮(zhèn)江 212013）

流體晃動是指部分充液的儲液罐在外部激勵作用下內(nèi)部流體產(chǎn)生運動的現(xiàn)象。在實際工程中流體晃動產(chǎn)生的液動壓力作用于結(jié)構(gòu)，對其產(chǎn)生不可忽略的影響，例如唐山大地震中流體晃動使罐壁與底板之間的角焊處發(fā)生斷裂破壞從而導(dǎo)致儲油的泄露[1]，Tokachi-oki地震中流體晃動使儲液罐浮頂下沉從而引發(fā)火災(zāi)[2]等。在工程上通常采用隔板降低流體晃動的幅度，從而減小了流體晃動對結(jié)構(gòu)的影響；在理論上為獲得流體晃動的各階模態(tài)并服務(wù)于后續(xù)的動力學(xué)分析，有必要進行流體晃動的特性研究，因此研究儲液罐中的流體晃動特性具有一定的工程應(yīng)用和理論價值。

通過模態(tài)分析主要可獲得儲液系統(tǒng)的固有頻率和各階陣型，通過模態(tài)分析可以避免激勵頻率和儲液系統(tǒng)的固有頻率發(fā)生共振，從而為在工程上的應(yīng)用提供依據(jù)。目前已有許多文獻研究了隔板對流體晃動的影響，其中就包括模態(tài)分析，并已取得了豐碩的理論成果。Chu 等[3]研究了多個相同隔板條件下的流體晃動問題，發(fā)現(xiàn)系統(tǒng)的固有頻率隨著隔板上方的有效水深的變化而變化。Ebrahimian 等[4]用邊界元法獲得了軸對稱儲液系統(tǒng)的固有頻率和振型，其研究表明隔板的位置對固有頻率的影響更大。Wang等[5]對帶有單個或多個相同隔板的環(huán)形儲液系統(tǒng)進行了研究，發(fā)現(xiàn)隔板的位置主要對第1 階模態(tài)的影響比較大。針對帶單層隔板的渡槽，房忠潔等[6]用半解析方法說明隔板對速度勢分布的影響比較大。有些學(xué)者對圓柱形儲液系統(tǒng)進行了大量的研究，如楊唱等[7]通過對其研究發(fā)現(xiàn)隔板參數(shù)與防晃效果之間的關(guān)系。同樣地，Wang 等[8]分析了多層相同隔板對流體晃動效應(yīng)的影響。隨著計算機技術(shù)的快速發(fā)展，數(shù)值模擬也經(jīng)常被用來解決帶隔板的儲液系統(tǒng)中流體晃動問題。陳更等[9]對帶隔板的液艙進行了數(shù)值模擬，其研究表明縱隔板可以更好抑制液艙中流體的晃動。Jin 等[10]通過數(shù)值模擬研究了水平多孔隔板附近的流體晃動特性問題，為理論研究提供了一個依據(jù)。

綜上所述，這些文獻主要研究了單個或多個相同隔板對流體晃動的影響，鮮有研究兩個不同半徑環(huán)形剛性隔板的控制機理，而文獻[11]中的流體子域法是一種半解析法，能夠同時滿足求解問題的高效性和高精度，因此本文基于流體子域法研究了兩個不同半徑環(huán)形剛性隔板對流體晃動特性的影響。

文獻[12]指出存在多層相同隔板的情況下，下層隔板對流體晃動的影響比較小，故本文在此主要考慮兩層隔板情況，并且上隔板的內(nèi)徑大于下隔板，其目的是為了凸顯下隔板對于晃動特性的影響。為了使所有的子域具有連續(xù)的邊界條件，引入8 個人工界面將儲液罐中的流體區(qū)域劃分為8 個子域，利用疊加原理和分離變量法求出各子域的速度勢的試函數(shù)，將其代入子域間的連續(xù)條件與自由液面的動力學(xué)邊界條件，得到關(guān)于待定系數(shù)與晃動頻率的級數(shù)方程，通過廣義傅里葉展開將級數(shù)方程轉(zhuǎn)換成線性方程組，從而得到關(guān)于頻率與模態(tài)的特征方程。利用求解廣義特征值的方法確定待定系數(shù)，從而使問題得到解決。

1 基本方程

圖1 為帶兩層隔板的圓柱形儲液罐，儲液罐內(nèi)半徑為R3，上隔板內(nèi)半徑為R2，下層隔板內(nèi)半徑為R1。如圖1 所示。R1、R2、R3滿足關(guān)系：R1＜R2＜R3。本文主要研究儲液罐中流體的晃動特性，因此罐體與隔板均假設(shè)為剛性。以儲液罐底板的中心為坐標原點，建立如圖1所示的柱體坐標系Orθz，上層隔板的位置設(shè)為z2，下層隔板的位置設(shè)為z1，液面高度設(shè)為H。

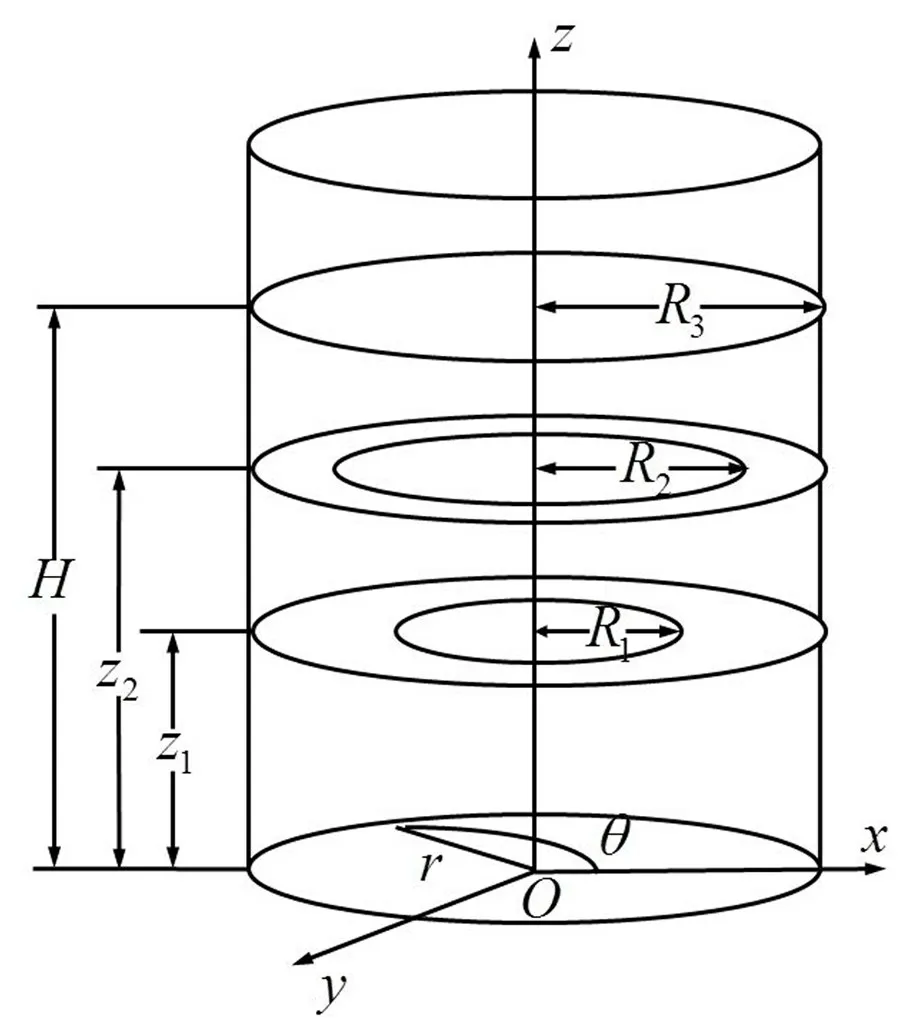
圖1 帶兩層隔板的圓柱形儲液罐

按照圖2 所示的子域劃分方法，將儲液罐中的流體區(qū)域劃分成8 個子域Ωi(i=1,2,…,8)，Sk(k=1,2…,8)為相鄰子域間的人工界面。將子域Ωi的速度勢函數(shù)設(shè)為φi，由于儲液罐中的流體為無旋、無黏、不可壓縮的理想流體，因此任意子域的速度勢函數(shù)滿足如下拉普拉斯方程：

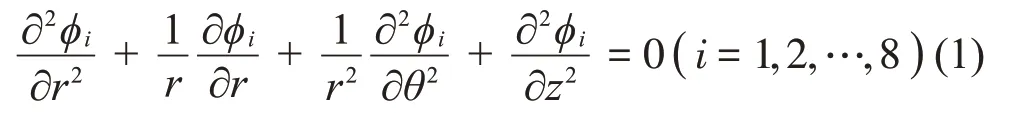
在柱坐標系下，流體域Ωi中每一點的速度為[12]：

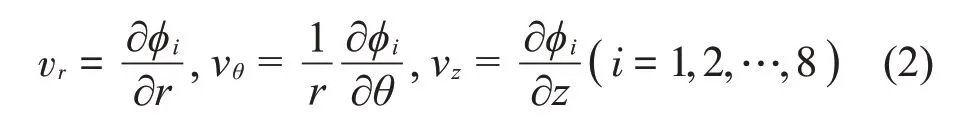
如圖2所示。流體子域在流-固耦合界面上需滿足固壁邊界條件，因此各子域的速度勢函數(shù)在罐壁上應(yīng)滿足如下邊界條件：

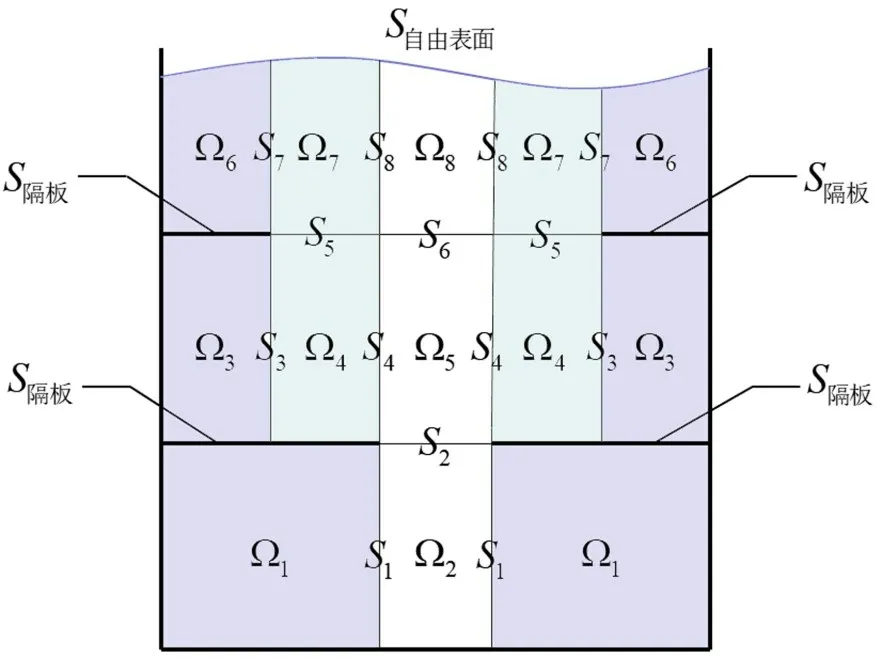
圖2 流體子域的劃分

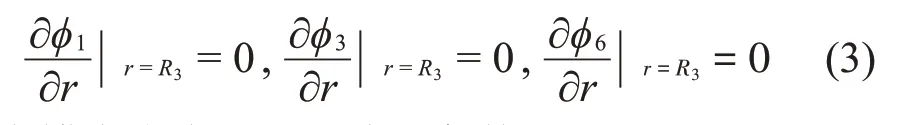
在罐底應(yīng)滿足如下邊界條件：

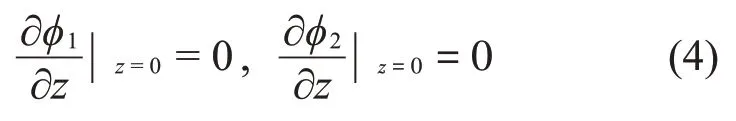
在隔板上應(yīng)滿足如下邊界條件：

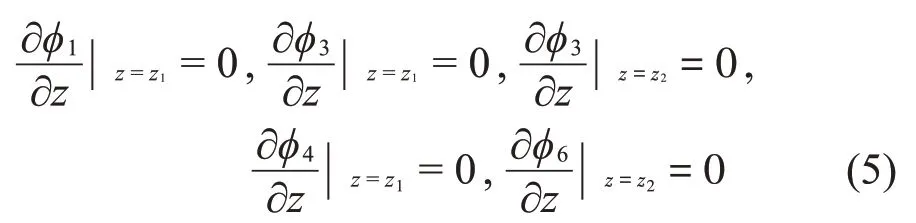
柱形子域的速度勢函數(shù)應(yīng)滿足如下邊界條件：

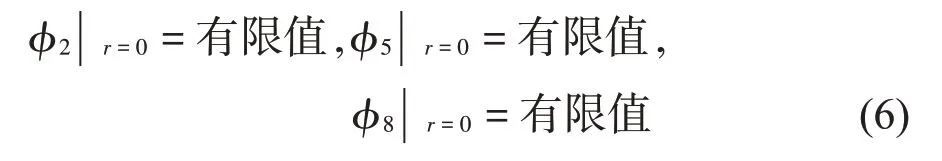
本文考慮流體做微幅線性晃動，根據(jù)Bernoulli方程，流體子域Ω6、Ω7以及Ω8在自由液面上應(yīng)滿足如下邊界條件：

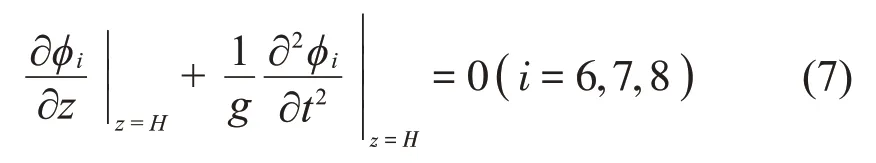
相鄰子域在其界面上應(yīng)該滿足壓力及速度連續(xù)條件，即有：

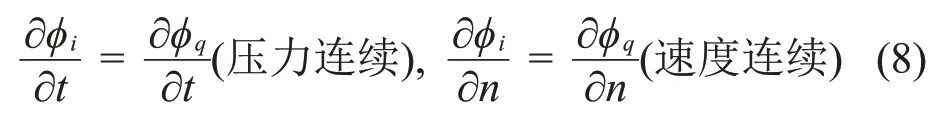
式中：n為人工界面Sk上的法向單位矢量；i、q為相鄰的子域。

2 子域速度勢函數(shù)求解

當儲液罐中流體發(fā)生自由晃動時，可以將流體速度勢函數(shù)設(shè)為如下形式[13]：

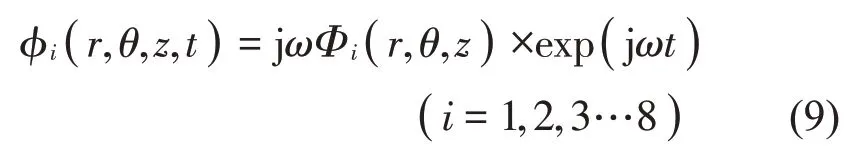
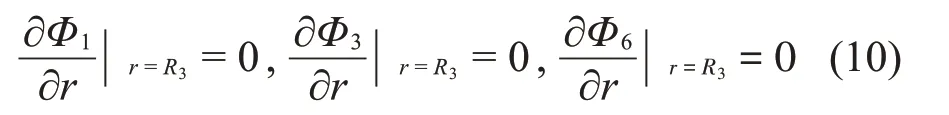
在罐底應(yīng)滿足如下邊界條件：

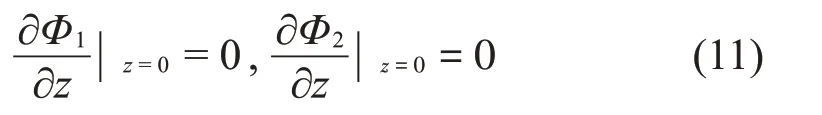
在隔板上應(yīng)滿足如下邊界條件：

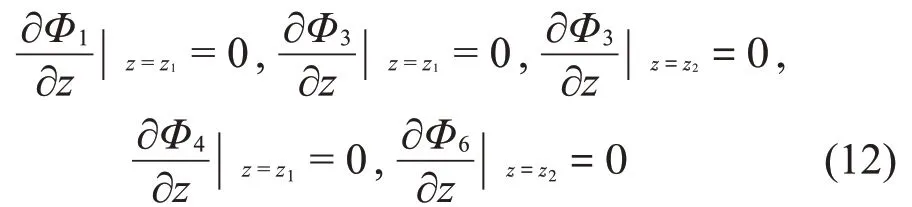
位于中心區(qū)域的速度勢函數(shù)應(yīng)滿足如下邊界條件：

Φ2|r=0=有限值,Φ5|r=0=有限值。

流體子域Ω6、Ω7以及Ω8的振型函數(shù)在自由液面上應(yīng)滿足如下邊界條件：

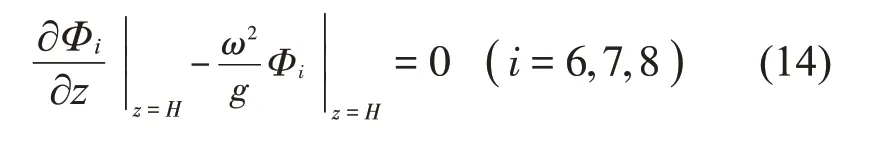
相鄰子域在其界面上應(yīng)該滿足壓力及速度連續(xù)條件，即有：

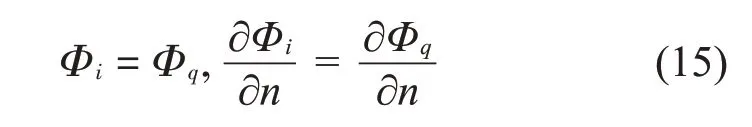
式中：n為人工界面Sk上的法向單位矢量；i、q為相鄰的子域。

根據(jù)疊加原理，對各子域的振型函數(shù)進行分解，結(jié)果如圖3 所示，圖3(a)所示為環(huán)柱形子域，圖3(b)所示為柱形子域，圖3(a)中的細點畫線表示子域的對稱軸。子域6、7、8 中的上實線為零壓力邊界條件，其余所有實線均為剛性邊界條件，虛線代表非齊次性邊界條件，即有：

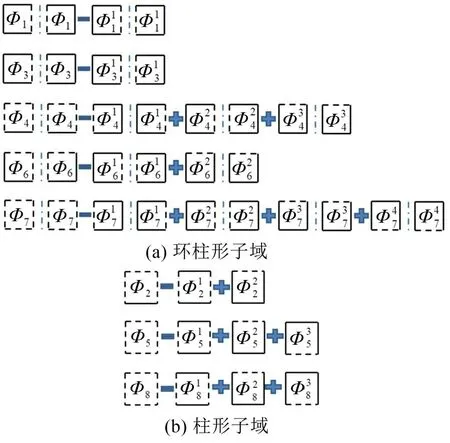
圖3 振型函數(shù)分解示意圖

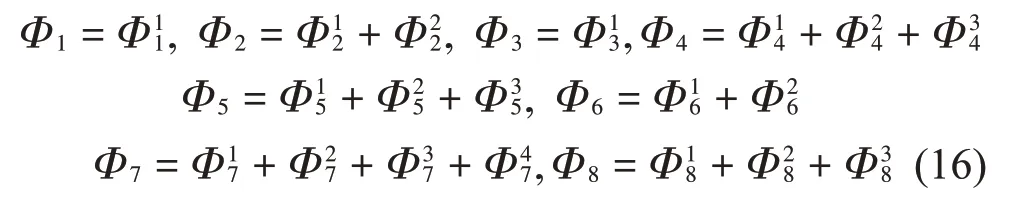
根據(jù)式(16)，對于子域Ω1，振型函數(shù)的分量Φ11應(yīng)滿足如下邊界條件：

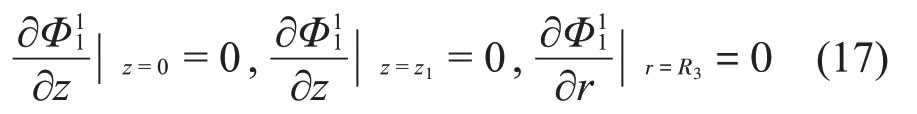
對于子域Ω2，振型函數(shù)的分量Φ12、Φ22應(yīng)滿足如下邊界條件：

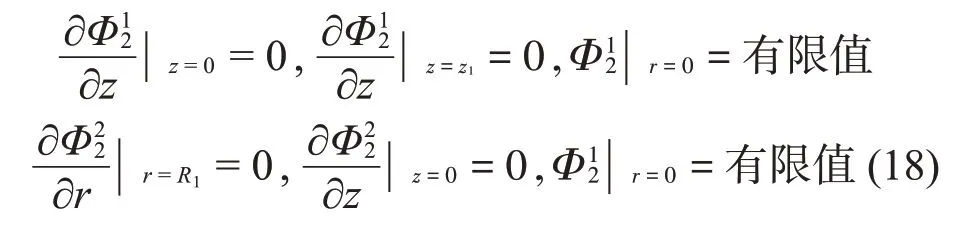
對于子域Ω3，振型函數(shù)的分量Φ13應(yīng)滿足如下邊界條件：

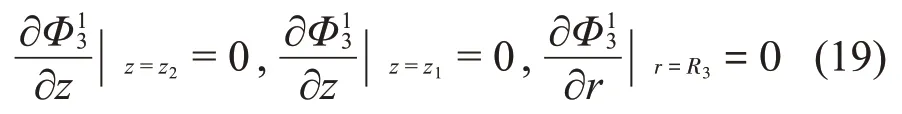
對于子域Ω4，振型函數(shù)的分量Φ14、Φ24、Φ34應(yīng)滿足如下邊界條件：

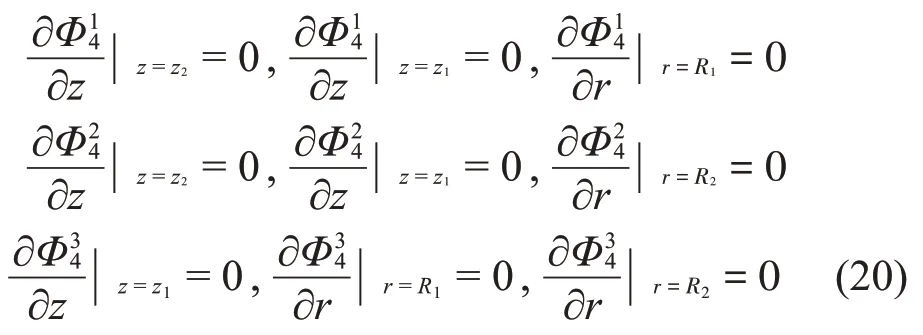
對于子域Ω5，振型函數(shù)的分量Φ15、Φ25、Φ35應(yīng)滿足如下邊界條件：

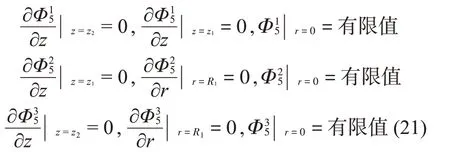
對于子域Ω6，振型函數(shù)的分量Φ16、Φ26應(yīng)滿足如下邊界條件：

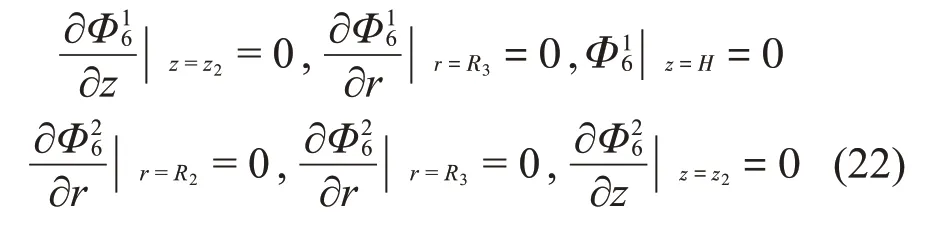
對于子域Ω7，振型函數(shù)的分量Φ17、Φ27、Φ37、Φ47應(yīng)滿足如下邊界條件：

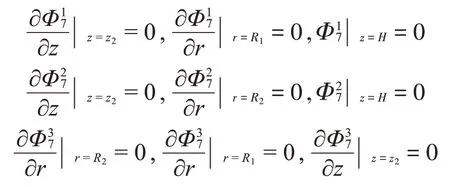
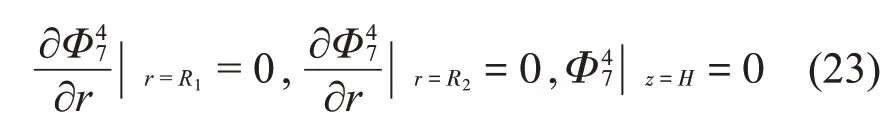
對于子域Ω8，振型函數(shù)Φ18、Φ28、Φ38應(yīng)滿足如下邊界條件：

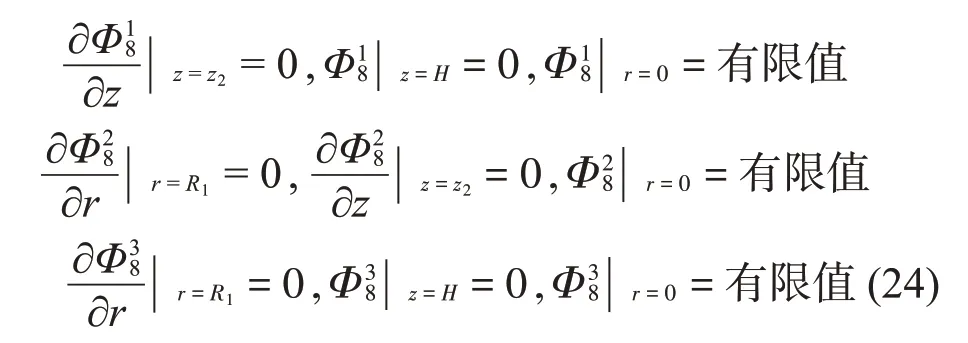
根據(jù)式(17)至式(24)，利用分離變量法可求得各個分量的試函數(shù)，再根據(jù)式(16)可得各個子域振型函數(shù)的形式解。將振型函數(shù)代入式(14)～式(15)中可以得到19 個級數(shù)線性方程組。根據(jù)三角函數(shù)和貝塞爾函數(shù)的正交性，消除級數(shù)方程中的空間坐標，并將方程截斷至N，從而得到有關(guān)待定系數(shù)的線性方程組，即有：

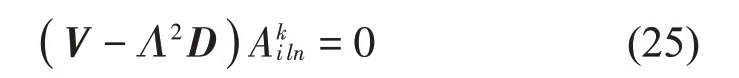
式中，矩陣V、D中的非零元素為級數(shù)方程展開后的系數(shù)；Λ為無量綱化后的晃動頻率，滿足：

級數(shù)方程(25)中的Λ2定義為廣義特征值，通過求解廣義特征值的方法確定和的數(shù)值。將代入振型函數(shù)就可以確定各個子域的速度勢函數(shù)。

3 收斂性和比較研究

首先進行收斂性分析，表1和表2分別對應(yīng)于上層隔板參數(shù)變化時的前3 階晃動頻率，從表中可以發(fā)現(xiàn)，隨著截斷項數(shù)的增加，晃動頻率會逐漸趨于精確解。雖然隔板參數(shù)對晃動頻率的收斂性會有一定的影響，但這種影響會隨著截斷項數(shù)的增加而逐漸減小，當截斷項數(shù)足夠大時，該影響可忽略不計。當N=26時，表1和表2中的晃動頻率均可保證4位有效數(shù)字，因此在下面的分析中，截斷項數(shù)均取26。

表1 (l=0,1,n=1,2,3)隨截斷項數(shù)N變化的收斂性（R1=0.2/m;R3=1/m;z1=0.4/m;z2=0.8/m;H=1/m)

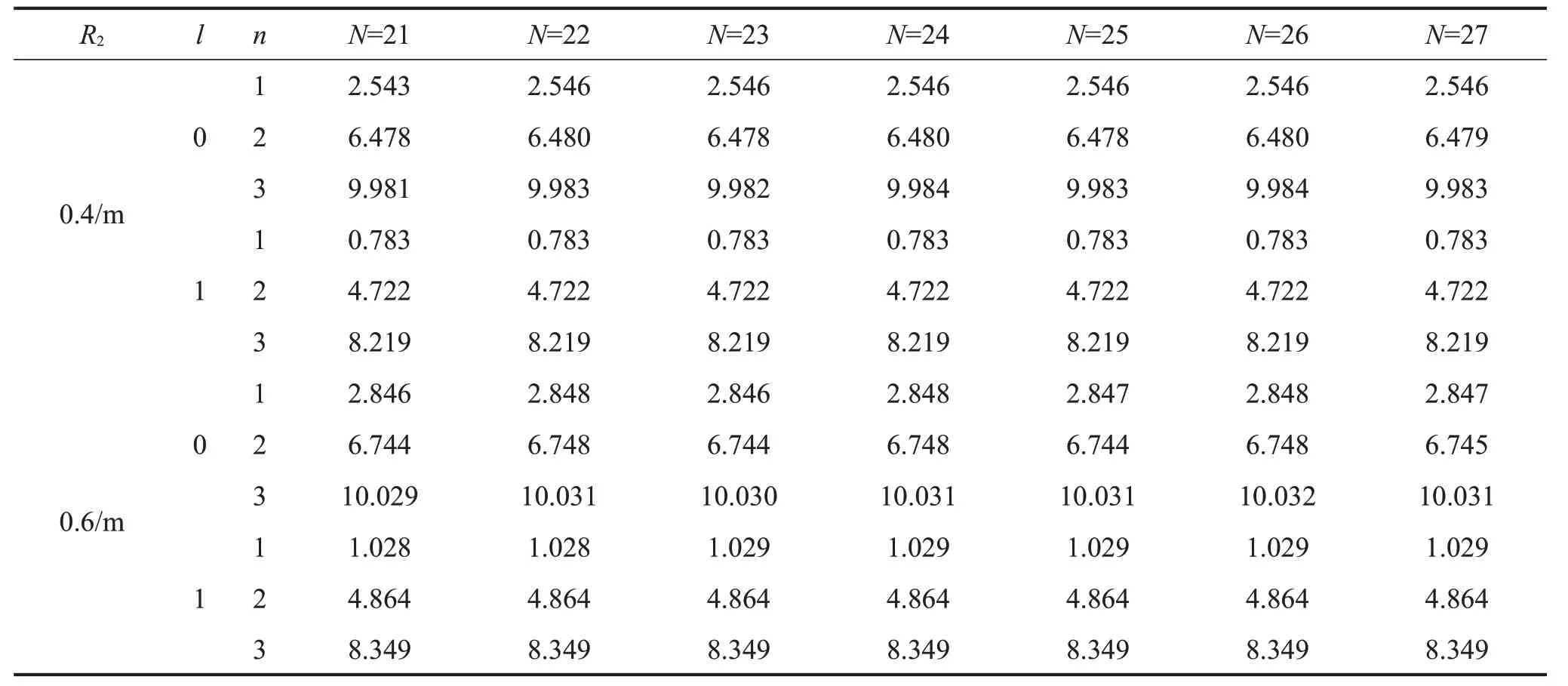
表1 (l=0,1,n=1,2,3)隨截斷項數(shù)N變化的收斂性（R1=0.2/m;R3=1/m;z1=0.4/m;z2=0.8/m;H=1/m)

R2 0.4/m 0.6/m l 0 1 0 1 n 1 2 3 1 2 3 1 2 3 1 2 3 N=21 2.543 6.478 9.981 0.783 4.722 8.219 2.846 6.744 10.029 1.028 4.864 8.349 N=22 2.546 6.480 9.983 0.783 4.722 8.219 2.848 6.748 10.031 1.028 4.864 8.349 N=23 2.546 6.478 9.982 0.783 4.722 8.219 2.846 6.744 10.030 1.029 4.864 8.349 N=24 2.546 6.480 9.984 0.783 4.722 8.219 2.848 6.748 10.031 1.029 4.864 8.349 N=25 2.546 6.478 9.983 0.783 4.722 8.219 2.847 6.744 10.031 1.029 4.864 8.349 N=26 2.546 6.480 9.984 0.783 4.722 8.219 2.848 6.748 10.032 1.029 4.864 8.349 N=27 2.546 6.479 9.983 0.783 4.722 8.219 2.847 6.745 10.031 1.029 4.864 8.349

表2 (l=0,1,n=1,2,3)隨截斷項數(shù)N變化的收斂性（R1=0.3/m;R2=0.6/m;R3=1/m;z1=0.2/m;H=1/m）

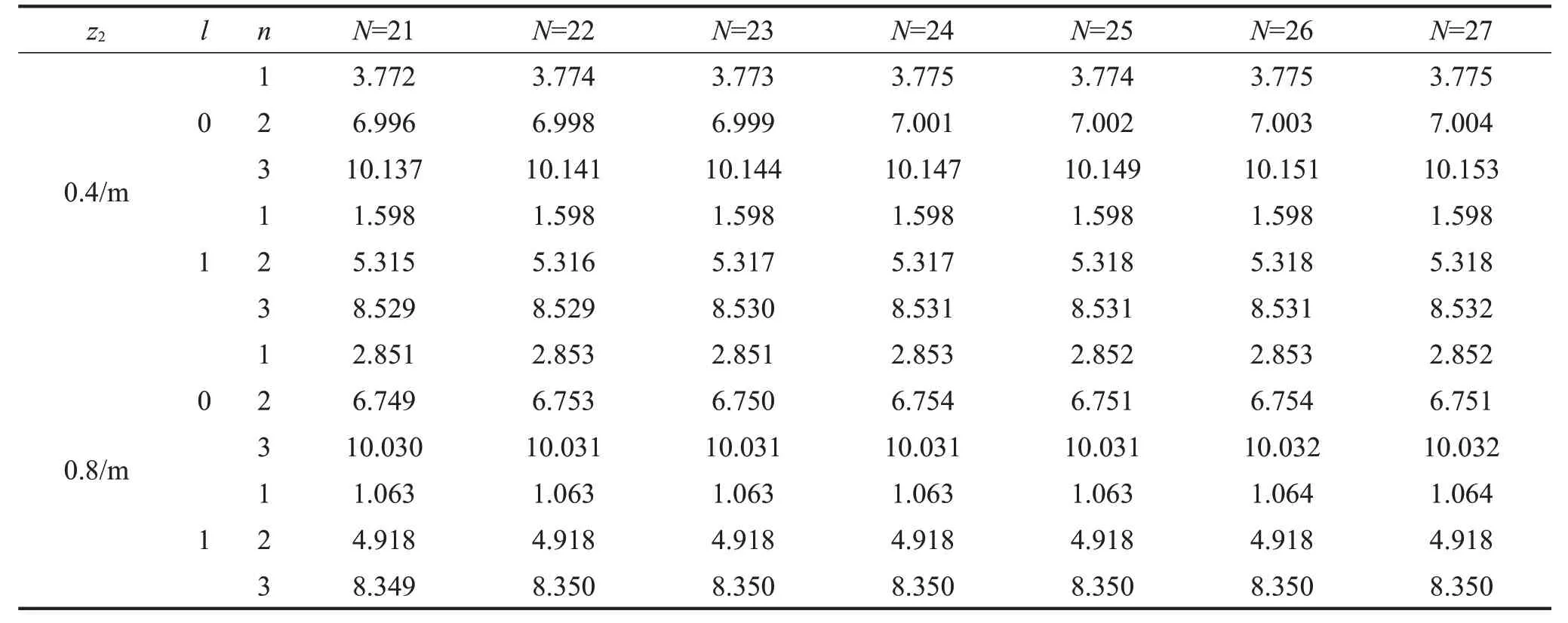
表2 (l=0,1,n=1,2,3)隨截斷項數(shù)N變化的收斂性（R1=0.3/m;R2=0.6/m;R3=1/m;z1=0.2/m;H=1/m）

z2 0.4/m 0.8/m l 0 1 0 1 n 1 2 3 1 2 3 1 2 3 1 2 3 N=21 3.772 6.996 10.137 1.598 5.315 8.529 2.851 6.749 10.030 1.063 4.918 8.349 N=22 3.774 6.998 10.141 1.598 5.316 8.529 2.853 6.753 10.031 1.063 4.918 8.350 N=23 3.773 6.999 10.144 1.598 5.317 8.530 2.851 6.750 10.031 1.063 4.918 8.350 N=24 3.775 7.001 10.147 1.598 5.317 8.531 2.853 6.754 10.031 1.063 4.918 8.350 N=25 3.774 7.002 10.149 1.598 5.318 8.531 2.852 6.751 10.031 1.063 4.918 8.350 N=26 3.775 7.003 10.151 1.598 5.318 8.531 2.853 6.754 10.032 1.064 4.918 8.350 N=27 3.775 7.004 10.153 1.598 5.318 8.532 2.852 6.751 10.032 1.064 4.918 8.350

為驗證本文方法的正確性，使用通用有限元軟件ADINA對本文模型進行模態(tài)分析，得到了流體晃動的頻率和模態(tài)。表3 對本文方法解和ADINA 解進行了比較。結(jié)果表明，本文計算的結(jié)果和ADINA有限元軟件模擬的結(jié)果具有較好的一致性，其最大相對誤差為0.65%，最小相對誤差為0.02%。因此本文方法滿足求解問題的高精度要求。

表3 (l=0,1,n=1,2,3)的比較研究（R1=0.35/m;R3=1/m;z1=0.5/m;z2=0.8/m;H=1/m）

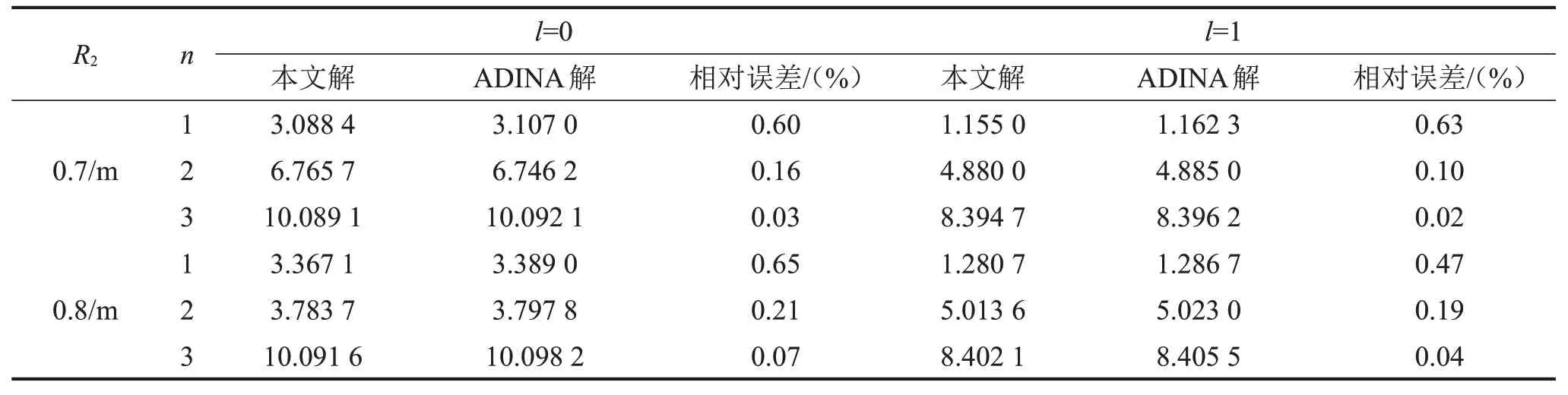
表3 (l=0,1,n=1,2,3)的比較研究（R1=0.35/m;R3=1/m;z1=0.5/m;z2=0.8/m;H=1/m）

R2 0.7/m 0.8/m n 1 2 3 1 2 3 l=0本文解3.088 4 6.765 7 10.089 1 3.367 1 3.783 7 10.091 6 ADINA解3.107 0 6.746 2 10.092 1 3.389 0 3.797 8 10.098 2相對誤差/（%）0.60 0.16 0.03 0.65 0.21 0.07 l=1本文解1.155 0 4.880 0 8.394 7 1.280 7 5.013 6 8.402 1 ADINA解1.162 3 4.885 0 8.396 2 1.286 7 5.023 0 8.405 5相對誤差/（%）0.63 0.10 0.02 0.47 0.19 0.04

4 參數(shù)研究

首先研究了上層隔板內(nèi)半徑和上層隔板位置對流體晃動特性的影響，結(jié)果如圖4和圖5所示。從圖中發(fā)現(xiàn)，當上層隔板的內(nèi)半徑接近儲液罐的內(nèi)半徑時，晃動頻率將不再受上層隔板的影響，此時下層隔板對流體晃動的頻率起主導(dǎo)影響。但當隔板的位置靠近自由液面時，圖5中曲線的斜率降低很快，表明上層隔板的位置是影響流體晃動最主要的因素。因此對上層隔板的位置進行優(yōu)化設(shè)計能夠有效減弱流體的晃動。

圖4 Λ2l1(l=0,1)隨上層隔板內(nèi)徑的變化曲線（R1=0.2/m;R3=1/m;z1=0.2/m;H=1/m）

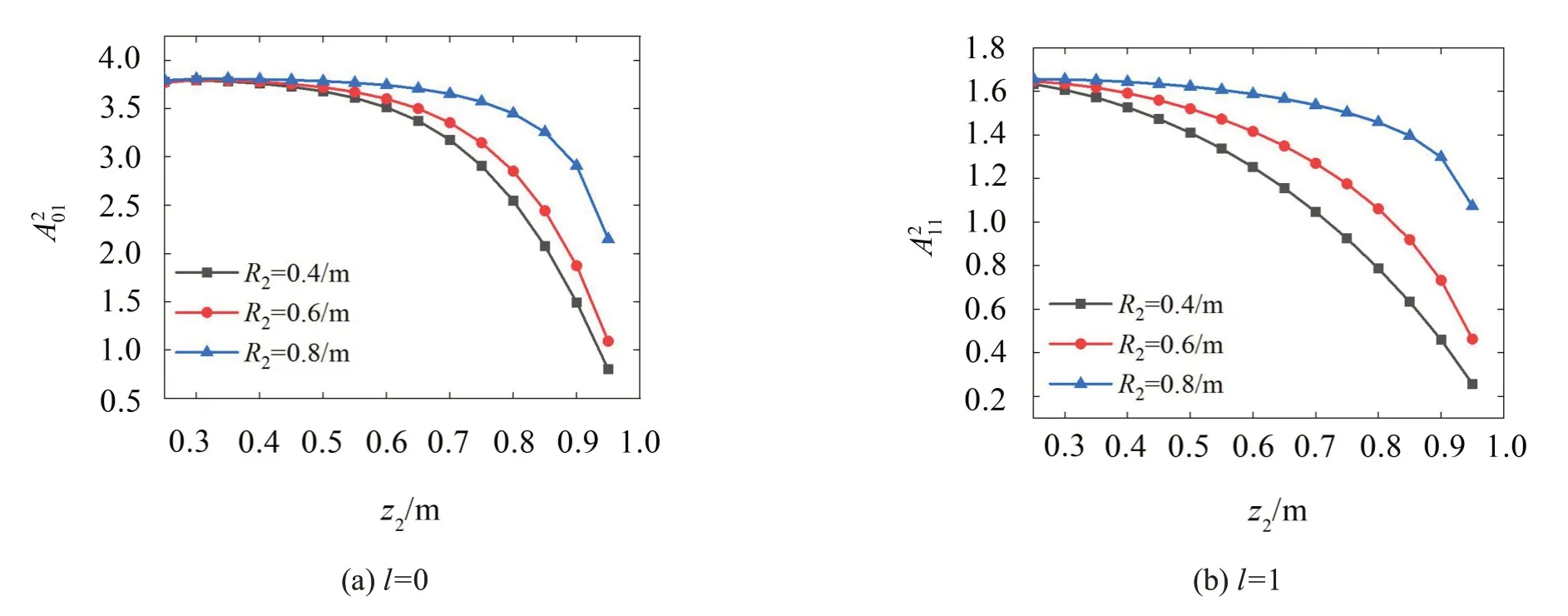
圖5 (l=0,1)隨上層隔板位置的變化曲線（R1=0.2/m;R3=1/m;z1=0.2/m;H=1/m）

其次研究了下層隔板內(nèi)半徑和下層隔板位置對流體晃動的影響，結(jié)果如圖6和圖7所示。下層隔板內(nèi)半徑對晃動頻率的影響隨著隔板位置的降低而減小，而這主要因為隔板接近于罐底時，隔板對流體晃動的影響很小。但當下層隔板的內(nèi)半徑逐漸減小時，對晃動頻率的影響也就越來越明顯。因此改變下層隔板的內(nèi)半徑仍然能夠明顯降低流體晃動的固有頻率，即也可達到抑制流體晃動的目的。

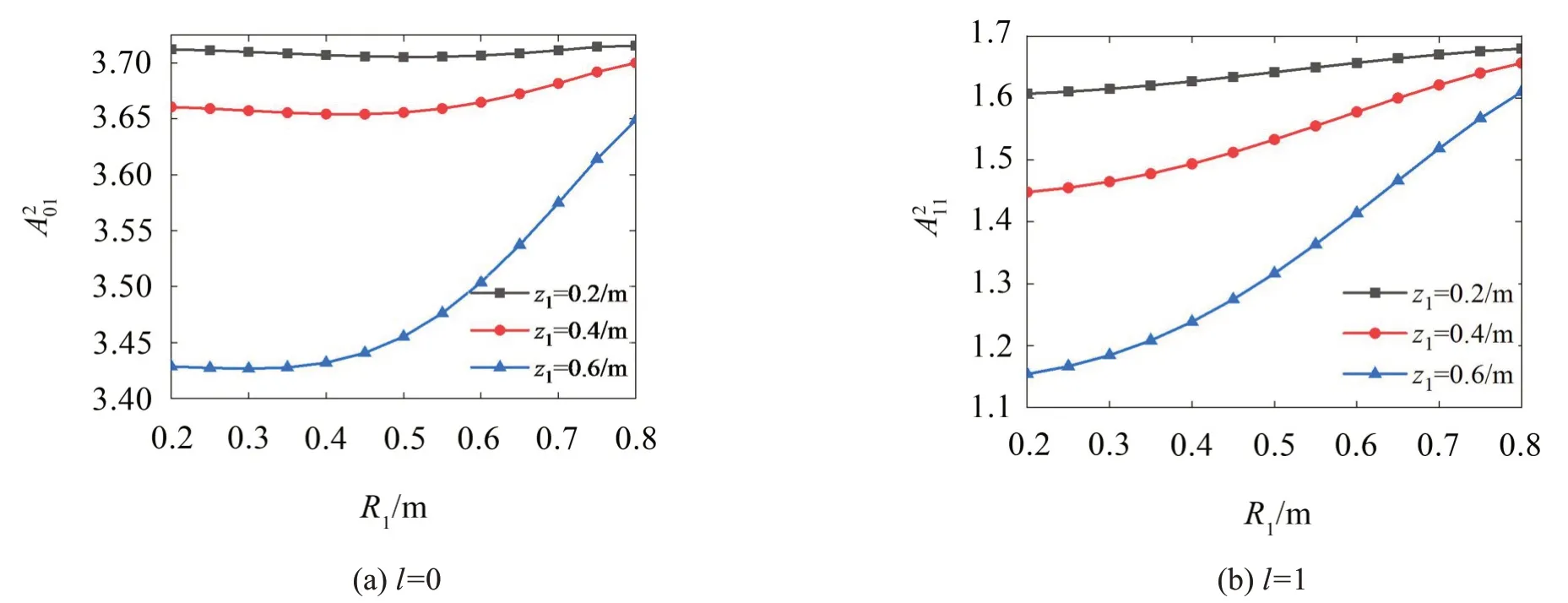
圖6 (l=0,1)隨下層隔板內(nèi)徑的變化曲線（R2=0.9/m;R3=1/m;z2=0.8/m;H=1/m）

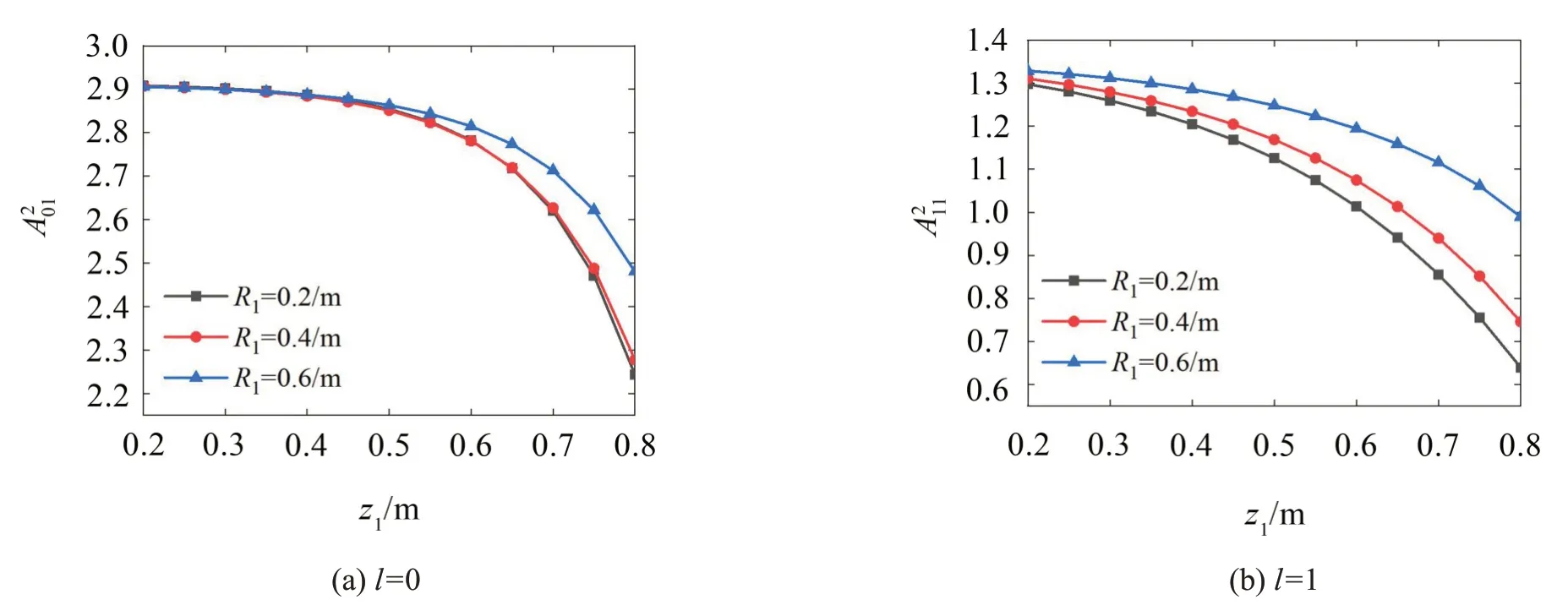
圖7 (l=0,1)隨下層隔板位置的變化曲線（R2=0.7/m;R3=1/m;z2=0.85/m;H=1/m）

將求得的流體晃動頻率代入方程式(25)就可以確定待定系數(shù)，將各個子域的振型函數(shù)代入方程式(9)就可以確定各個子域的速度勢函數(shù)。圖8和圖9 分別為環(huán)向波數(shù)為0 和1 的前兩階振型。很明顯，當環(huán)向波數(shù)為0時其表現(xiàn)為對稱振型，當環(huán)向波數(shù)為1時表現(xiàn)為反對稱振型。

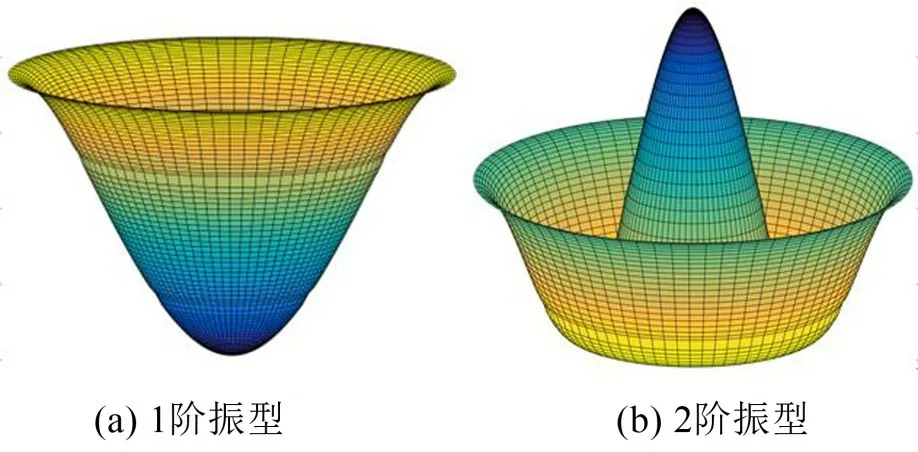
圖8 環(huán)向波數(shù)為0時的前兩階振型（R1=0.35/m;R2=0.7/m;R3=1/m;z1=0.5/m;z2=0.8/m;H=1/m）

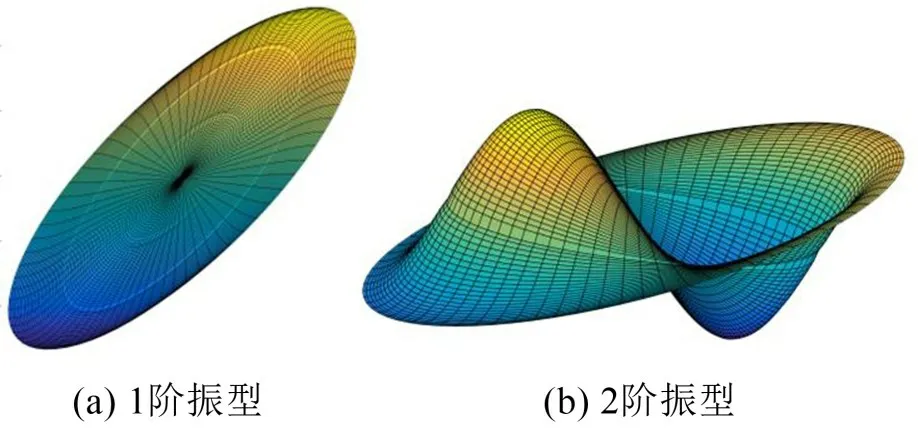
圖9 環(huán)向波數(shù)為1時的前兩階振型（R1=0.35/m;R2=0.7/m;R3=1/m;z1=0.5/m;z2=0.8/m;H=1/m）

5 結(jié)語

本文的主要創(chuàng)新點在于研究了兩個不同半徑環(huán)形剛性隔板對流體晃動的影響，文中隔板及罐壁均采用剛性材料，流體為理想流體。通過流體子域法求解了各個子域的速度勢函數(shù)，并與ADINA解進行比較驗證了本文方法的正確性，進而對流體的晃動特性進行了研究。本文中的模型只適合于流體做微幅線性晃動的情況。雖然本文的研究對象為帶兩層不同內(nèi)徑環(huán)形剛性隔板的儲液系統(tǒng)，但本文的研究方法可以進一步擴展到帶有任意個不同內(nèi)徑隔板的情況。

通過對參數(shù)的研究可以得到以下結(jié)論：存在兩層隔板的情況下，下層隔板的內(nèi)徑越小，對流體晃動的影響越明顯，但當下層隔板位置靠近罐底時，隔板內(nèi)徑的變化對流體晃動的影響越來越小；下層隔板內(nèi)徑越小，對環(huán)向波數(shù)l=0的影響越小。