基于CFD的火箭滑橇水剎車水動性能分析

李新穎，肖 軍，張家旭，胡 奇，孫 豐

（1.中國特種飛行器研究所，湖北荊門 448035；2.高速水動力航空科技重點實驗室，湖北荊門 448035；3.中國華陰兵器試驗中心，陜西華陰 714200）

火箭滑橇是以火箭發動機作為動力并沿專用的高精度直軌道運行的裝置，用以進行氣動力、材料、引信、制導與控制系統的沖擊和破壞實驗［1］。在火箭滑橇運動的終點段，往往需要對橇車進行制動和剎車以實現被試品與火箭滑橇分離或軟回收，為了減小制動時的阻力、過載和加速度，多采用水剎車方式［2］。水剎車的原理是當高速滑行的火箭滑橇進入制動段后，水剎車裝置將水槽里的水戽起，水流在水剎車內部旋轉一個角度后噴射出來，這樣橇車的動量轉換成了水的動量，從而獲得強大的制動力，達到快速剎車的目的［3］。由于水剎車具有經濟、靈活、制動能力大等特點，因此被廣泛應用于火箭滑橇試驗［4］。

火箭滑橇水剎車一般是在高速、大過載下運行的，各個裝置承受很大的作用力，工況極其惡劣，所以在設計過程中需要進行受力分析［5］，然而物理試驗往往面臨成本高、周期長等問題。 隨著計算流體力學（Computational Fluid Dynamics，簡稱CFD）和高性能計算機的發展和應用，CFD 技術在航空、航天、船舶和兵器等領域的水動性能預報方面發揮著越來越重要的作用，漸漸變成與物理試驗并駕齊驅的研究手段。CFD具有成本低、周期短、無縮尺比效應等優點，且能以較少的人力、物力和時間為物理試驗提供指導［6-7］。

本文針對火箭滑橇水剎車超高速（1Ma）戽水過程中的強非線性內外流耦合的氣水兩相流問題，提出了一種基于雷諾應力模型結合VOF方法的水動性能數值計算方法，研究了水剎車在不同航速、不同吃水下的水動性能。

1 幾何模型及研究工況

以某雙軌火箭滑橇三角形水剎車為研究對象，在數值計算時，對模型進行了簡化處理，見圖1。

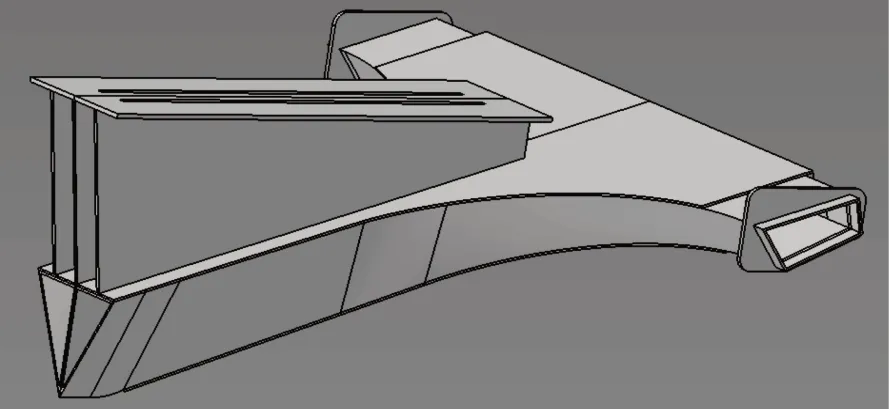
圖1 水剎車模型Fig.1 The water brake model

水剎車在制動段運動時，受戽斗入水口高度的限制，在速度不斷減小的情況下，制動力會越來越小，因此，為了保證一定的制動力，水剎車的吃水應逐漸增大，吃水基準線為水剎車最低點處，見圖2。數值計算時，取水剎車管道內壁5 個截面共38 個點進行壓力監測，見圖3，最終得到水剎車在不同航速、不同吃水下的水動阻力和局部壓力，研究工況見表1。

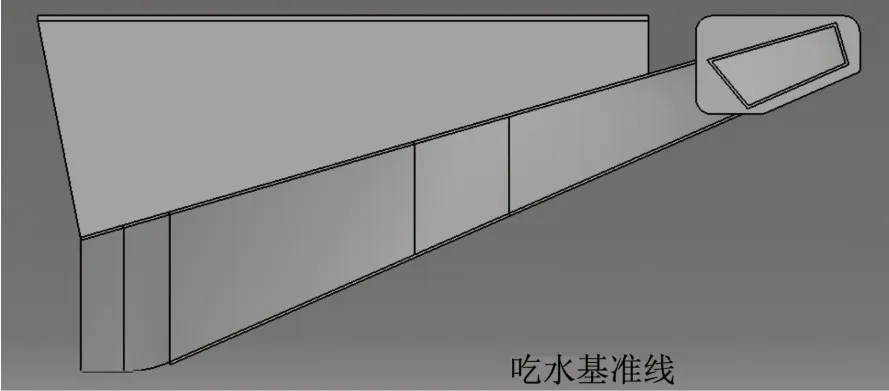
圖2 吃水基準線Fig.2 Draft baseline

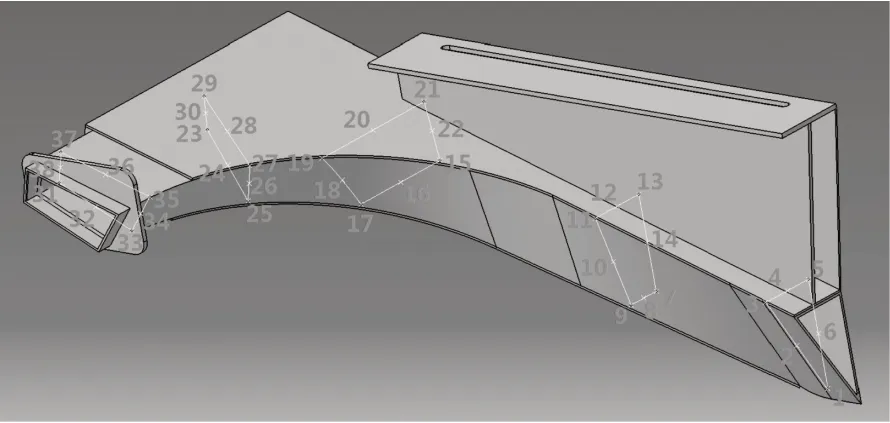
圖3 壓力監測點（半模）Fig.3 Pressure monitoring point (half model)

表1 研究工況Tab.1 Study cases

2 數值方法

2.1 控制方程

任何CFD 均是基于流體力學基本控制方程：連續方程、動量方程與能量方程［8］。針對水剎車水面超高速戽水過程中的氣水兩相流問題，若只對水動性能進行計算，則可考慮流動為等溫條件下的不可壓縮流動，即不考慮空氣和水的壓縮性，只考慮重力，故最終的方程形式如下所示。

連續方程：

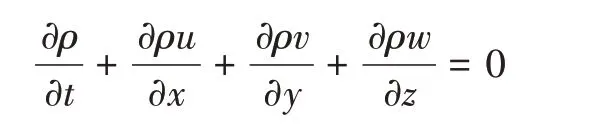
動量方程：

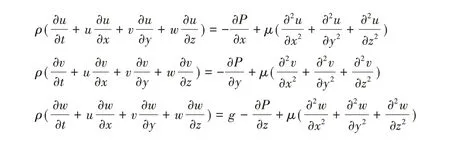
上式中，ρ為密度，t為時間，u、v、w分別為x、y、z方向上的速度分量，p為靜壓，μ為動力黏性系數，g為重力加速度。

為了精確模擬湍流運動、管道內流場和自由液面外流場，采用比常規兩方程模型（如k-ε和k-ω）精度更高的雷諾應力模型（Reynolds Stress Model（RSM，7方程））結合壁面函數法來模擬，離散方法采用有限體積法，空間離散格式采用二階迎風格式，時間離散采用隱式方法，離散方程的求解選用Coupled 方法，自由液面捕捉采用VOF方法。

2.2 雷諾應力模型

粘渦模型中雷諾應力采取了各種假設而達到了簡化，許多湍流流動的細節會被忽略，故不能很好地預測復雜流動。與粘渦模型不同的是，雷諾應力模型不采用Boussinesq 假設，而是直接對時均N-S 方程中的二階脈動相關項提出其相應的偏微分方程組，由于在方程組中還出現了湍流動能k及耗散率ε，故增加了相應的k與ε 方程，在求解時，需要額外求解6 個雷諾應力方程、k方程與ε方程。增加的雷諾應力微分方程考慮了更多的湍流細節，所以雷諾應力模型能更真實地模擬實際的湍流流動，反映其內在本質，這一模型的優點在于可準確地考慮各向異性效應［9-10］。

2.3 VOF方法

VOF方法根據各個時刻流體在網格單元中所占體積函數F來構造和追蹤自由液面，若在某時刻網格單元中F=1，則說明該單元全部為指定相流體所占據，為流體單元；若F=0，則該單元全部為另一相流體所占據，相對于前相流體則稱為空單元。當0＜F＜1時，則該單元為包含兩相物質的交界面單元［11］。F函數的控制方程可以寫成下列形式，即

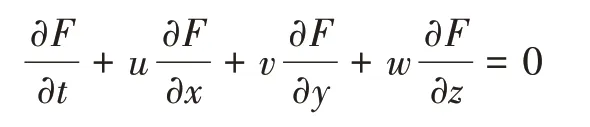
由于VOF 方法追蹤的是網格中的流體體積，而不是流體質點的運動，因而具有容易實現、計算量小和精度高等優點，并且可以處理自由液面大變形和拓撲結構發生變化等復雜三維情況［12］。

3 數值計算及分析

3.1 網格劃分

網格劃分時，采用非結構六面體的網格布局形式，取半模進行網格劃分和計算，計算域大小如下（L為模型縱向長度）：

（1）模型首部離前邊界（Inlet）：1L；

（2）模型尾部離后邊界（Outlet）：5L；

（3）自由液面離上邊界（Top）：2L；

（4）自由液面離下邊界（Bottom）：2L；

（5）模型對稱面離側邊界（Side）：2L。

沿航向模型表面布置約480 個網格，自由液面處的網格大小為X=Y=50Z=50×L/1000，模型首部、管道內部和流場變化劇烈區域的網格適當進行細化，添加邊界層網格，Y取40，最終網格量為2500 萬～3200 萬。網格示意圖見圖4-5。

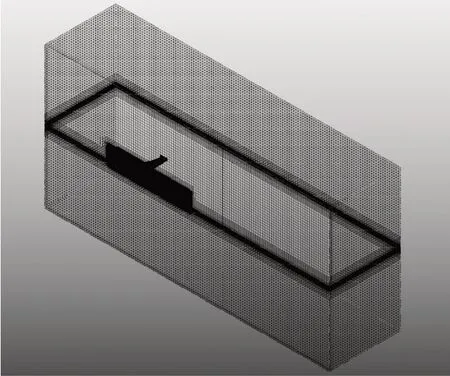
圖4 全局網格（航速340m/s，吃水40mm）Fig.4 Global mesh (speed = 340m/s、draft = 40mm)

圖5 模型網格（航速340m/s，吃水40mm）Fig.5 Model mesh (speed = 340m/s、draft = 40mm)

3.2 結果分析

數值計算時，模型壁面為無滑移邊界，即考慮黏性，最大非線性迭代次數為20，時間步長取ΔT=0.001L/V（V為航速）。

表2 為水動阻力計算結果與試驗結果，其中試驗結果依據試驗時的橇車質量和最大縱向加速度獲得。表3 為監測點的壓力值。圖6-圖10 為不同工況下的流場示意圖。

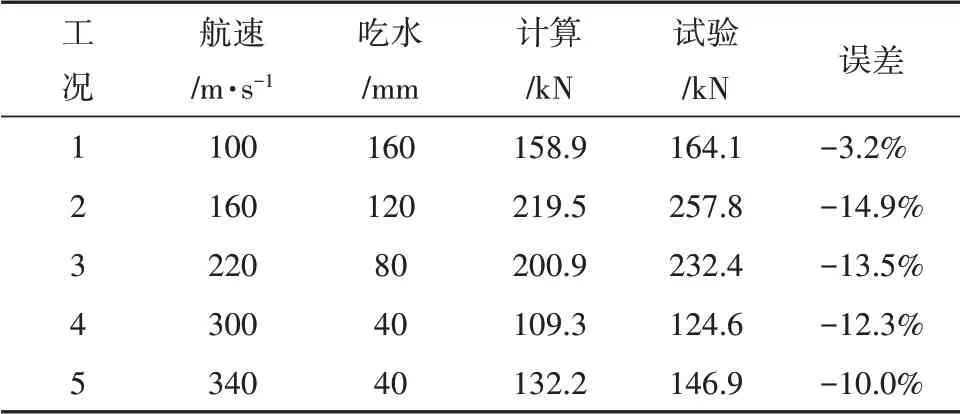
表2 水動阻力結果Tab.2 Hydrodynamic resistance results

圖6 流場示意圖（航速100m/s，吃水160mm）Fig.6 Figure of flow field (speed = 100m/s, draft = 160mm)

由表2 可以得出，水動阻力的數值計算精度達到85%；航速為160m/s、吃水為120 mm 時，水動阻力達到最大。由表3 可以得出，在水剎車水流入口處，由于與水存在撞擊，入口處的局部壓力較大；水剎車管道轉彎處和出口處，由于管道的離心作用和水流的沖擊作用，局部壓力較大。由圖6-圖10可以看出，水剎車在航行過程中，外部水流會沿水剎車外側面和下表面進行爬升直至流向尾部，內部水流會通過戽斗并經管道旋轉后向兩側噴出。

圖10 流場示意圖（航速340m/s，吃水40mm）Fig.10 Figure of flow field (speed = 340m/s, draft=40mm)

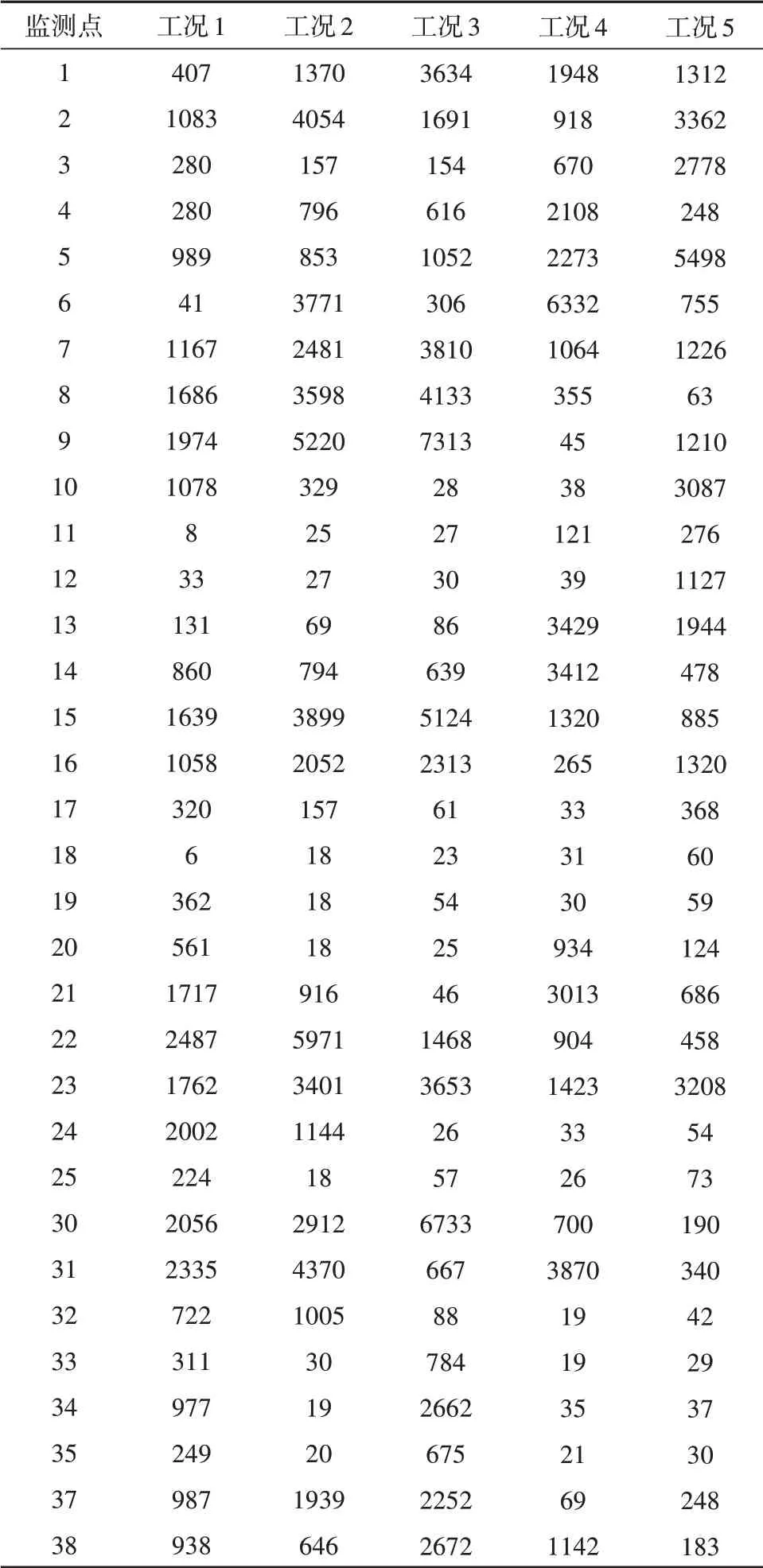
表3 監測點壓力值（KPa）Tab.3 Monitoring point pressure（KPa）

4 結論

采用雷諾應力模型結合VOF 方法對水剎車水面超高速戽水過程的水動性能進行了數值分析，計算精度達到85%，驗證了方法的可行性，為水剎車外形設計和強度校核提供技術支持；水剎車在航行過程中，外部水流會沿水剎車外側面和下表面進行爬升直至流向尾部，內部水流會通過戽斗并經管道旋轉后向兩側噴出；水剎車航速為160 m/s、吃水為120 mm 時的水動阻力最大，另外水剎車入口處、管道轉彎處和出口處的局部壓力較大，結構設計時應適當加強。

圖7 流場示意圖（航速160m/s，吃水120mm）Fig.7 Figure of flow field (speed = 160m/s, draft = 120mm)

圖8 流場示意圖（航速220m/s，吃水80mm）Fig.8 Figure of flow field (speed = 220m/s, draft = 80mm)

圖9 流場示意圖（航速300m/s，吃水40mm）Fig.9 Figure of flow field (speed = 300m/s, draft = 40mm)