空間除臭設計風量理論計算方法探究
于文俊 徐婷婷 周燕昭
1 北京市市政工程設計研究總院有限公司
2 北京時代桃源環境科技有限公司
0 引言
垃圾處理廠空間除臭的風量確定的方法有換氣次數法[1-2],數值模擬法[3-4]等。其中,以換氣次數法最為常用。
換氣次數法是根據以往工程經驗結合實際效果定性分析而定,簡單易行,但并無確切算法。在垃圾處理過程中,各空間尺寸差異巨大,臭氣逸散情況復雜,換氣次數法的合理性和準確性值得商榷。
數值模擬方法可以全面反映空間內氣流分布情況,能夠極大的優化除臭系統設計。但是,數值模擬計算時間長,邊界條件復雜,需要結合具體工程建模,缺乏普遍指導意義。
風量作為空間除臭系統設計的關鍵參數,既關系到空間環境質量是否合格,又影響系統的除臭效率和技術經濟性。其簡單適用的理論計算方法值得深入的探究。
1 除臭簡化模型及濃度函數推導
實際上,在通風過程中,空間內臭氣成分的物理和化學特性并未發生變化。通風過程只是一種耦合污染物散發與新風補入雙重因素而引發空間污染物濃度變化的過程[5-6]。建立合適的污染物擴散模型,對于工程設計和環境管理具有重要參考意義[7-8]。
為了明確持續通風作用下空間污染物濃度變化規律,假設空間內某種污染物的發生量為QPg/s,密度為ρg/m3;通風量為Lm3/s,其污染物濃度為C0g/m3;空間體積為Vm3,空間內污染物初始濃度為Cig/m3;在通風量L下,通風時間t時的污染物濃度為C。為了簡化模型,設定如下假設:
1)空間為廣義空間,即包括建筑空間、設備內空間等。
2)QP值由垃圾的物化特性決定,忽略通風對該值的影響,為定值。
3)L,C0為定值。
4)通風開始時間記為t=0。
5)污染物濃度C為時間t的連續函數。
6)通風后空間內空氣迅速混合并均勻。
為了探討污染物濃度C與時間t的關系,取一時間微元Δt,易有:污染物散發量為QPΔt,送風帶入的污染物總量為LC0Δt,根據質量守恒原理,可得,排風帶走的污染物總量為(L+(QP/ρ))C(ε)Δt。其中,空間內的污染物質量隨時間的變化量為QPΔt+LC0Δt-(L+(QP/ρ))C(ε)Δt。空間除臭簡化模型如圖1。
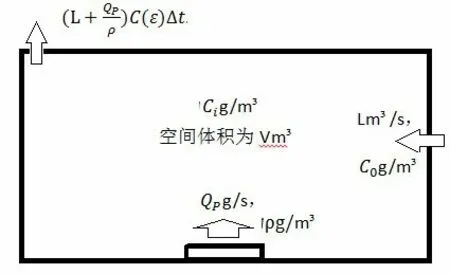
圖1 空間除臭簡化模型圖
結合污染物濃度的定義,很容易得到,空間內污染物平均濃度隨時間的變化量為:
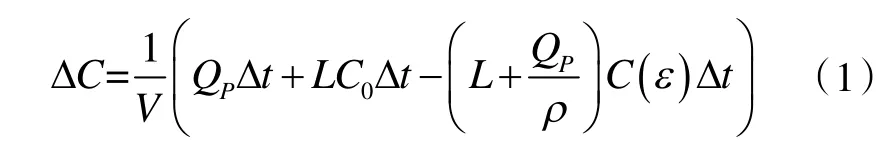
整理上式,即可得到空間內污染物平均濃度隨時間的變化率為:
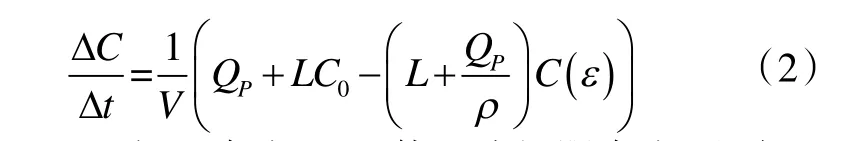
當Δt→0 時,必存在ε→t使上式極限存在,即有:
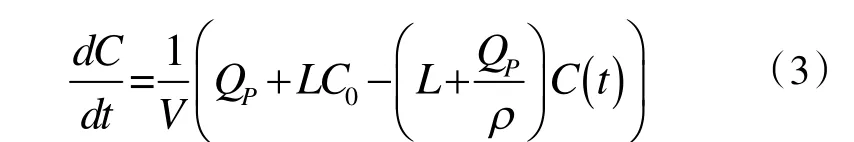
此式即為污染物濃度變化的基本方程。它是變量可分離的一階常微分方程,易求其通解為:
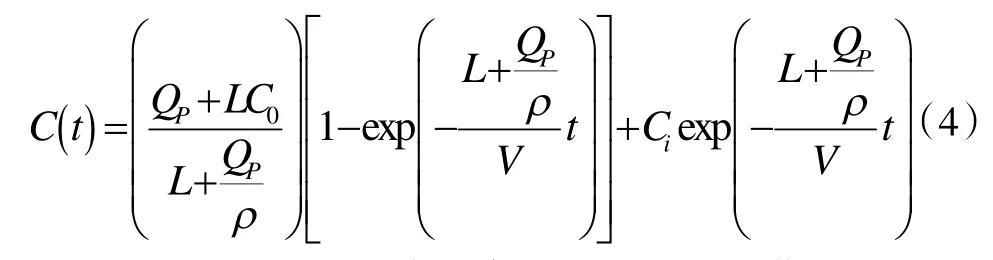
此式即為濃度函數,其闡述了在通風作用下空間內污染物濃度隨時間的變化關系。很容易看出,濃度函數隨時間的增長呈指數變化。這為計算不同時段空間內的污染物平均濃度提供了方便。
式中(L+(QP/ρ))/V項,分子為單位時間排風量,分母為空間體積,顯然,此項為單位時間的換氣次數。
令,
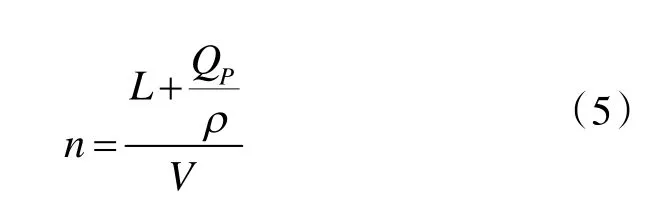
并整理式(4),得:
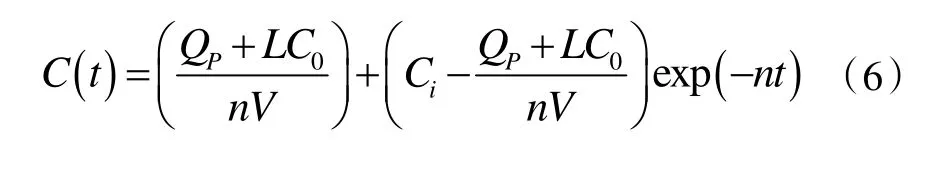
2 濃度函數分析
2.1 污染物體積散發項分析
相比文獻[9]中提到的建筑通風行業常用的稀釋方程,式(6)與其顯著的區別在于增加了QP/ρ項,該項為密度函數中的污染物體積散發項,表征的是單位時間污染物散發的體積。換言之,文獻[9]中忽略了污染物散發體積對整體通風體積的影響。
在常規的建筑通風中,污染源少,散發強度小,單位時間內污染物散發體積遠小于通風量,其對整體計算的影響可以忽略不計。然而,對于垃圾處理工程而言,情況不盡相同,原因如下:
1)垃圾處理工程中,污染物散發強度大,散發面積廣。散發量QP表征的是單位時間整個空間內的污染物的總散發質量。顯然,該值與空間內垃圾堆置體積、暴露面積等垃圾總量息息相關。在垃圾坑、堆肥車間等存在大量垃圾堆置的建筑空間內,該值對通風量的影響不容忽視。
2)為了抑制污染物無序散發,垃圾處理工程中的處理設施(設備、傳送帶等)常采取密閉措施并實施負壓控制。為了降低密封系統成本,保證密封的效果以及最大化的設備利用率,密閉處理設施內的通風空間一般較小。并且為了避免補風波動影響系統負壓,一般不設置單獨的主動補風,主要以縫隙滲透補風為主(卸料、檢修工況除外)。基于上述原因,密封設施內的通風量一般較小。尤其地,垃圾處理過程中的振動、翻轉、壓縮等擾動會強化污染物散發,使污染物散發量明顯高于平時。綜合考慮上述因素,散發量QP對通風量的影響不可忽略。
另外,QP/ρ項是公式中進出口風量平衡的關鍵項。平衡方程缺少此項,違背質量守恒原則。
綜上所述,考慮密度函數的準確性和普遍適用性,推薦在設計應用時計算此項,尤其是在垃圾污染物重點散發區域和通風空間狹小區域。
2.2 極限分析
對t→+∞時的C(t)函數極限進行求解:
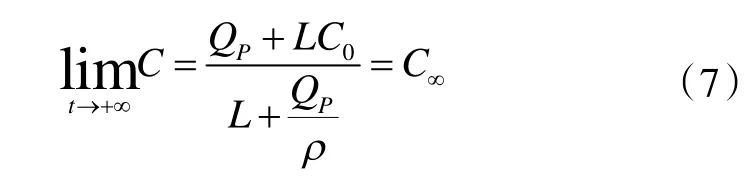
可見,當t→+∞時,空間內的污染物平均濃度有極限濃度C∞。該濃度與時間和空間無關,只與污染物密度,散發量,通風量有關。
式(QP+LC0)/(L+(QP/ρ))中,分子為空間內單位時間污染物質量增加量,分母為單位時間的排風量。因此,該式可以理解為在持續通風作用下,穩定狀態時排風口的污染物濃度。顯然,隨著時間的增長,空間內污染物平均濃度逐漸趨近于穩定狀態下排風口的污染物濃度。
1)特例分析
特別地,式(7)存在下述工況(表1):

表1 兩個特例
其中,工況1 表明,若密閉空間內不存在污染物散發源,無論空間內初始濃度如何,在持續通風作用下,空間內污染物平均濃度將逐漸趨近于新風中的污染物密度C0。該工況適用于檢修或卸料完成后(檢修門或卸料門關閉,且無其他散發源),在持續通風作用下最終的空間內污染物平均濃度判斷;工況2 表明,若密閉空間內存在穩定的污染物散發源且未采取任何通風措施,隨著時間的延長,空間內污染物平均濃度將逐漸趨近于污染物密度ρ。該工況適用于長時間無通風作用的密閉空間內污染物平均濃度判斷。
2)極限風量
除上述工況外,為分析通風與空間內污染物設計濃度的一般關系,整理式(7)如下:
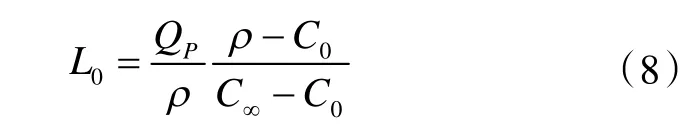
將L0定義為極限通風量。其意義在于:對于任一個特定的濃度限值,總有一個通風量與其匹配,這為確定設計風量提供了方便。值得注意的是,式(8)應用的前提是t→+∞,換言之,設計風量并不能夠直接的取用L0。
2.3 濃度函數增減性分析
雖然設計風量不能直接取用L0,但是分析濃度函數C(t)特點可知,必然存在某一風量可使空間污染物濃度在有限的時間內達到設計濃度C,這一風量即為設計風量L。設計風量的取用范圍取決于濃度函數的增減性。
由上,對式(4)求導,可得
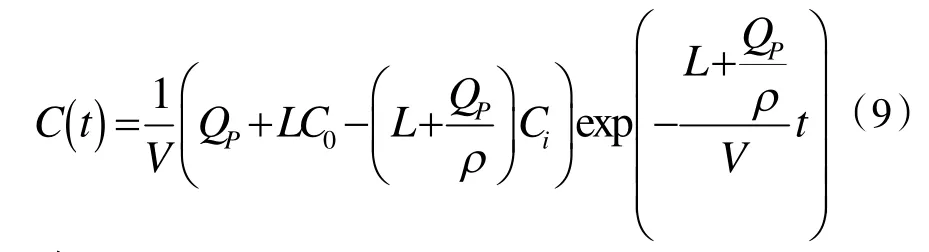
令:
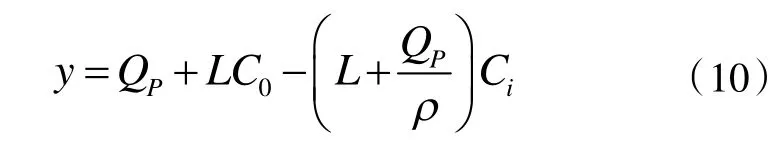
顯然,C(t)增減性由y的正負決定。
結合設計濃度C、初始濃度Ci和新風中的污染物濃度C0討論式(4)的增減性如表2:
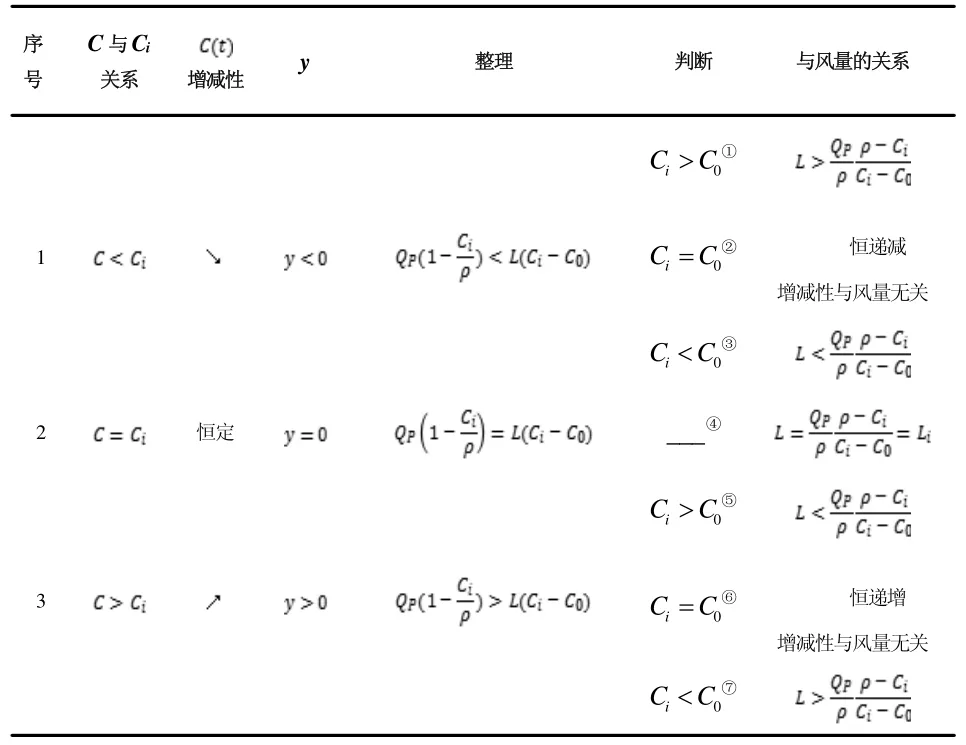
表2 增減性與風量關系表
正如表1 工況2 所述,空間內僅有該種污染物(全部充滿此種氣體,無其他氣體存在)時,污染物濃度Ci與污染物的密度ρ相等,此時污染物濃度最大。然而,在垃圾處理工程中,空間內存在多種污染物,即空間內的污染物濃度Ci恒小于該污染物的密度ρ,即Ci<ρ。因此表2 第②種工況不存在。
同樣,易推出表2 第③種工況中,L<0。其含義是與模型定義方向相反的通風。此種工況稱為轉移工況,既將臭氣由低濃度(Ci)空間轉移至高濃度(C0)空間,再由高濃度空間內的除臭系統統一收集處理。類似地,在表2 第⑦種工況中,當時,也可用于轉移工況。實際上,本文研究的重點在于設計通風量L>0 時空間濃度的變化情況,因此轉移工況不予討論。
相對地,在表2 第⑦種工況中,只要存在任意L>0,濃度函數均遞增。
令
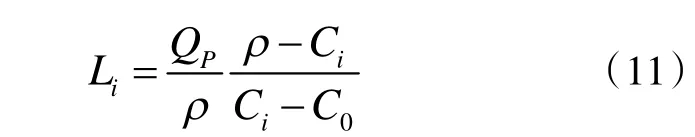
將Li定義為臨界風量,其實際意義在于Li是濃度函數C(t)增減性的分界點。顯然,Li并不總是大于0,其正負取決于Ci與C0的關系。
綜上所述,設計風量L>0 時,具備實際意義的討論簡化為表3 四種工況。
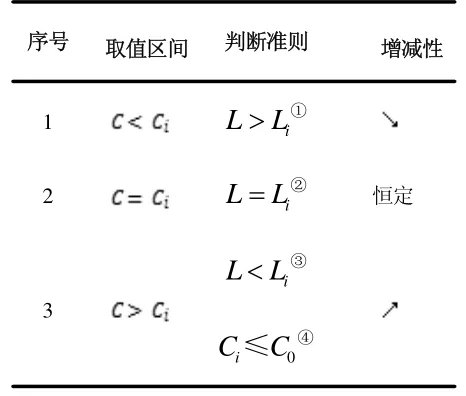
表3 增減性判斷準則
顯然,濃度函數C(t)在定義域內具有單調性,其增減性與臨界風量Li有關。濃度函數C(t)的增減趨勢可以表示如圖2:
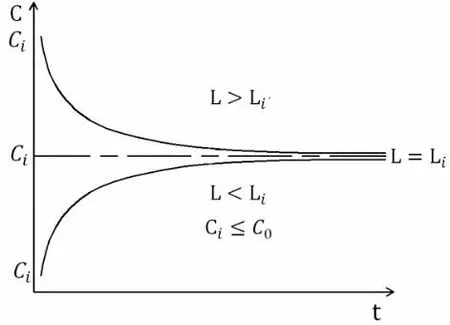
圖2 濃度函數C(t)趨勢圖
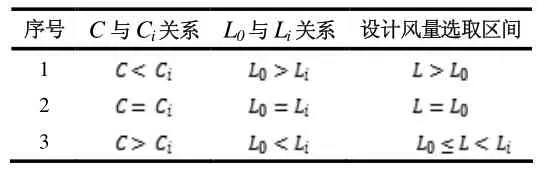
顯然,通風并不總是具有“稀釋”作用(空間污染物濃度隨時間增長而減小)。當L 值得注意的是,雖然Li與L0的公式相近,但并不等同。首先,由于C并不總是等于Ci,因此兩式并不相等;其次,臨界風量決定函數的增減性,而極限風量決定空間污染物濃度能夠無限趨近的極限值。 令 容易判斷,L是關于C'的遞減函數。 利用式(12),根據C和Ci的大小關系,即可判斷與其分別對應的L0與Li的關系;結合表3 即可做出設計風量選取區間推斷,如表4。 表4 設計風量選取區間 因為L是關于C' 的遞減函數,若L 由上,設計風量選取區間推薦如表5: 表5 設計風量選取區間 特別地,當L→L0-,濃度偏差小于工程許可范圍時,表4 中②或④工況仍可酌情采用。 一般而言,滿足本節選用規則的設計通風量,均能使空間污染物濃度達到設計要求,區別只在于所需時間不同。 換氣次數法簡便快捷,工程中應用普遍,通常根據以往工程經驗確定。本文嘗試從理論出發探討其估算方法。 結合上文,分析式(12)可知,當L→L0時,C→C∞。若C與C∞的偏差縮小到一定范圍,工程上可近似的認為滿足要求。 基于此,引入偏差α,令 則有: 假設已知實際濃度C,初始濃度Ci以及允許偏差值α,聯立式(4)、(7)、(14)可得: 令N=nt,整理上式得: 其中,N的含義為:空間內平均污染物濃度達到實際濃度C時所需要的總換氣次數。從此式可以看出,總換氣次數與時間、空間無關,僅與C、Ci和α有關。值得注意的是,總換氣次數(次)與設計中常用的單位時間換氣次數(次/h)并不相同,其關系為N=nt。另外,α在定義時,并未明確其正負,因此,正負偏差均適用于此式;α的取值范圍可以根據各工程實際情況確定。 1)濃度函數具有單調性,隨時間增長呈指數變化。 2)進行垃圾處理工程除臭計算時,濃度函數中考慮污染物體積散發項QP/ρ是必要的。 3)t→+∞時,空間內污染物平均濃度與時間和空間無關,只與污染物特性,散發量,通風量有關。 4)通風并不總是具有“稀釋”作用,當L 5)濃度函數存在極限,其增減性與臨界風量有關。 6)結合臨界風量和極限風量分析,給出設計風量推薦選用區間及計算流程,并推導了總換氣次數的估算公式。3 設計風量的選取
3.1 風量選取區間
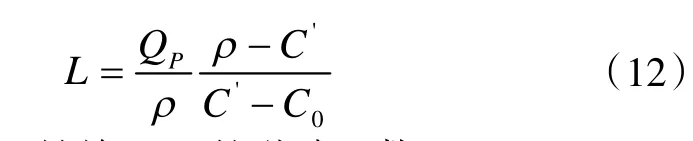

3.2 總換氣次數估算

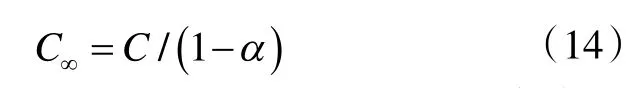
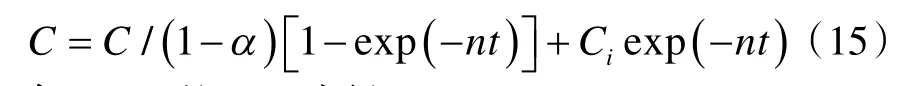
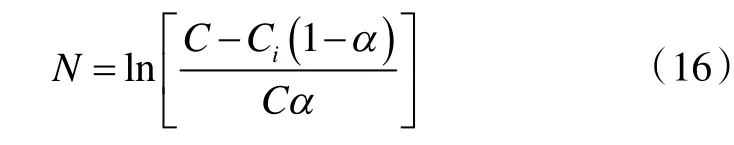
4 結論

