美英早期幾何教科書中的等腰三角形性質與判定

錢秦 汪曉勤

【摘 要】 選取1800—1959年間出版的103本英美早期幾何教科書，研究發現教科書中關于等腰三角形性質——“等邊對等角”的證明方法共有六種，即歐幾里得的方法、帕普斯的方法、勒讓德的方法、萊斯利的方法、作高法和實驗操作法.而關于等腰三角形判定定理——“等角對等邊”的證明方法共有七種，即歐幾里得的反證法、想象有兩個三角形、大邊對大角、作頂角角平分線、作底邊的高、做底角的角平分線和實驗操作法.早期教科書中的等腰三角形知識，為今日教學提供了豐富素材.

【關鍵詞】 等腰三角形;等邊對等角;等角對等邊;美英早期教科書

1 引言

在平面幾何中，三角形的“等邊對等角”“大邊對大角”“等角對等邊”“大角對大邊”是對三角形邊角關系的定性刻畫，是三角學中邊角定量關系的基礎.在西方數學史上，《幾何原本》卷一命題5（等腰三角形底角相等）是一個著名的幾何定理，被稱為“驢橋定理”，既因為歐幾里得在證明該定理時所用的圖形像一座簡單的桁架橋，也因為它阻擋了許多中世紀的學習者進一步學習《幾何原本》后續命題的腳步.

關于等腰三角形的性質和判定，我國現行五種初中數學教材（人教版、北師大版、滬教版、浙教版及蘇教版）的內容安排大同小異.在引入上，五種教材均設計了折紙活動;在“等邊對等角”的證明上，人教版和北師大版教材通過作底邊的中線，利用SSS定理加以論證，而滬教版和浙教版教材通過作頂角的平分線，利用SAS進行說理，而蘇教版教材除折紙驗證外，并未給出具體的說理過程.關于“三線合一”性質，浙教版教材設計了以“幾何畫板”為工具的探究活動，而另四種教材均通過“等邊對等角”加以說理.關于“等角對等邊”，北師大版教材僅僅作輔助線的提示而未給出完整的證明，其余四版教材均通過作頂角平分線，運用AAS定理進行說理[1-4].已有的教學設計大多從教材出發，通過剪紙、折疊引入新課，個別教師運用了數學史.

不難發現，關于等腰三角形的性質與判定，現行教科書傾向于作輔助線（中線、角平分線）來構造全等三角形，但這幾種方法的合理性受到人們的質疑.如，在《幾何原本》中，SSS定理（命題I.8）的證明用到了三角形的唯一性（命題I.7），而三角形唯一性的證明又需要用到“等邊對等角”（命題I.5），這就使得涉及SSS定理的證明具有循環論證之嫌.而角平分線（命題I.9）的存在性又要用到SSS定理，使得作角平分線的合理性也得不到保證[1].鑒于此，我們聚焦等腰三角形性質與判定，對19世紀初至20世紀中葉的美、英幾何教科書進行考察，試圖回答以下問題：關于等腰三角形的性質與判定，早期幾何教科書中采用了哪些證明方法？證明方法有何演變規律？對今日課堂教學有何啟示？

2 教科書的選取

本文從有關數據庫中選取1800—1959年間出版的103種美英早期平面幾何教科書作為研究對象，其中85種出版于美國，18種出版于英國.在選取的過程中，對于同一作者再版的書籍，若相關內容無明顯差異，則視為同一種;若內容有明顯差異，則視為不同的教科書.以20年為一個時間段，各教科書的分布情況如圖1所示.

早期幾何教科書的章節劃分不像今天一般細致清晰，有的教科書甚至未劃分章節，直接以一個個命題的形式呈現.103種幾何教科書中，等腰三角形主題所在章節主要有“命題”“直線形”“三角形”“等腰三角形”“線、角與直線圖形”“全等三角形”等.表1為具體分布情況.我們也發現，無論章節名如何，本節內容在各教材中所處的位置都比較靠前.由此可以說明，等腰三角形的性質與判定是平面幾何的一個基礎內容.

等腰三角形的性質主要有“等邊對等角”和“三線合一”，但大部分教材中，“三線合一”并未給出論證，而是將其作為“等邊對等角”的推論直接給出.判斷一個三角形是否為等腰三角形時，可以根據定義，也可通過“等邊對等角”來判斷.因此，本文將從“等邊對等角”和“等角對等邊”兩個角度梳理早期教科書中的證明方法.

3 “等邊對等角”的證明

考察發現，在103種教科書中，有2種只提示學生作輔助線，通過三角形全等進行證明，但未給出完整的證明過程;101種教科書給出了完整的證明，證明方法大致可分為6類：歐幾里得的方法、帕普斯的方法、勒讓德的方法、萊斯利的方法、作高法、實驗操作法.

3.1 歐幾里得的方法

歐幾里得的偉大貢獻在于公理化體系的建立，其《幾何原本》從給定的少數公理、公設及定義出發，用邏輯推論方法推導了四百多個命題[2].“等邊對等角”作為《幾何原本》第一卷命題5，其證明過程嚴格遵循公理化體系，只用到了命題5之前的公設、公理及命題.

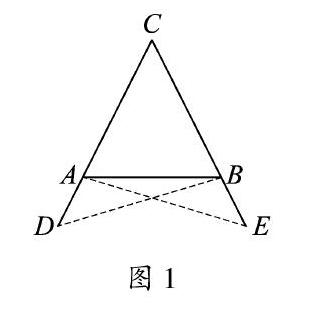
有10種教科書沿用了歐幾里得的證明.如圖1，在等腰△ABC中，CA=CB.在兩腰CA和CB的延長線上取兩點D，E，使得AD=BE，并連接AE和BD，則CD=CE.由SAS定理，可證△CAE≌△CBD，故有∠CAE=∠CBD;再由SAS定理，可證△BAE≌△ABD，故有∠EAB=∠DBA.根據“等量減等量，差相等”，得∠CAB=∠CBA[3].

3.2 帕普斯的方法

11種教科書采用了古希臘數學家帕普斯（Pappus，公元3世紀末）的方法：將等腰三角形△CAB和△CBA看作兩個三角形，然后用SAS證明△CAB≌△CBA.

也許有人會認為，把一個三角形看作兩個三角形，對學生來說較為抽象，于是把另一個三角形“外化”出來了.如圖2，已知等腰△ABC，CA=CB.想象△ABC被拿起、翻轉后放下，記作△A′B′C′（A′，B′，C′分別對應A，B，C）.那么，AC=A′C′=BC=B′C′，則在△ABC和△A′B′C′中，AC=B′C′，BC=A′C′，且∠C=∠C′.根據SAS定理有△ABC≌△B′A′C′，則∠A=∠B′，又因為∠B=∠B′，等量代換得∠A=∠B[4].

3.3 勒讓德的方法

法國數學家勒讓德（A. M. Legendre，1752—1833）通過作底邊中線的方法來構造全等三角形，從而得到“等邊對等角”.有4種教科書采用他的方法.如圖3，在等腰△ABC中，CA=CB.過點C作底邊AB的中線CD.由SSS定理可證△CAD≌△CBD，則∠A=∠B[5].

3.4 萊斯利的方法

蘇格蘭數學家萊斯利（J. Leslie， 1766—1832）的方法有69種教科書采用.如圖4，在等腰△ABC中，CA=CB.過頂點C作∠BCA的角平分線，交AB于點D.根據定理SAS可證△ACD≌△BCD，故得∠A=∠B[6].

3.5 作高法

4種教科書采用作高法.給定CA和CB為等腰△ABC中相等的兩邊，作CD⊥AB交AB于點D，如圖5.在Rt△CAD和Rt△CBD中，CA=CB，CD=CD，根據HL定理，可證△CAD≌△CBD，所以∠A=∠B[7].

3.6 實驗操作法

有5種教科書采用了實驗操作（折疊）.如圖6所示，通過尺規作圖構造一個等腰△CAB，小心地將三角形從紙上剪下.沿底邊AB的中線將三角形折疊，并比較∠CAB和∠CBA的大小.接著再構造不同尺寸的等腰三角形，同樣比較兩個底角的大小.我們觀察到，等腰三角形的底角是相等的[8].

3.7 證明方法的演變

19世紀初至20世紀中期，早期教科書中呈現了豐富的方法來解決這個問題.以20年為一個時間段，圖7給出了“等邊對等角”的六種證明方法在每個時間段的分布.

由圖7可見，在考察的整段時間，教科書用來說明“等邊對等角”的方法呈現多元化的特點，但始終以萊斯利的作角平分線方法為主流.歐幾里得延長兩腰的做法，由于其嚴密的邏輯及在幾何上的獨特地位，使它在兩千多年后的教科書中仍占有一席之地.帕普斯的方法，巧妙地將三角形對應的部分重合，在歷史上流行了很長一段時間.但隨著更簡便的作輔助線（角平分線、底邊中線及高）證明三角形全等的方法出現，歐幾里得和帕普斯的方法逐漸淡出了歷史舞臺.到了20世紀，實驗幾何開始受到人們的重視，一些教科書相應設計了折紙的實驗操作來豐富學生的直觀體驗.

那么，是否如引言中提到的質疑一樣，一些證法存在著邏輯上的漏洞呢？今天，人們對“等邊對等角”某些證法的質疑主要依據的是《幾何原本》的體系.然而，本文所考察的美英早期幾何教科書采用了不同的邏輯體系，不同的邏輯體系就造成了知識點編排順序的差異.勒讓德在《幾何基礎》中采用了圖8所示的命題順序[5]，SSS定理并未建立在等腰三角形性質之上，他通過作底邊中線來證明“等邊對等角”，是完全合理的.萊斯利則采用了圖9所示的命題順序[6]，其通過作角平分線證明“等邊對等角”，也是嚴謹的.

4 “等角對等邊”的證明

“等角對等邊”，即如果三角形中有兩個角相等，那么其對邊相等，這個三角形為一個等腰三角形.83種教科書給出了完整的證明，證明方法大致可分為以下7種.

4.1 歐幾里得的反證法

23種教科書沿用了歐幾里得的反證法.如圖10，令∠CAB=∠CBA.假設對邊AC比另一邊BC要長，令AD=BC，那么△DBA明顯要比△ABC小.但因為CB與BA及其夾角∠CBA等于DA與AB其夾角∠DAB，故知△DAB≌△CAB，這是不可能的（大小不同的三角形不全等）.因此，AC不能比BC長.類似可證明BC不能比AC長，所以BC=AC[9].

4.2 想象有兩個三角形

11種教材采用“想象兩個三角形”的方法.如圖11，給定△ABC，其中∠A=∠B.假設△A′B′C′是△ABC的一個復制品，將△A′B′C′翻轉后放在△ABC上，那么B′將落在A上，A′將落在B點，則B′A′與AB重合.因為∠A′=∠B′，∠A=∠A′，等量代換得∠A=∠B′，所以B′C′將與AC重合.類似地，A′C′將與BC重合.因此，C′將同時落在AC和BC上，即C′落在它們的交點C上.所以，B′C′=AC.又有B′C′=BC，則AC=BC[10].

4.3 大邊對大角

6種教科書先證明“大邊對大角”，再由此說明“等邊對等角”.如圖12，給定△ABC，其中∠A=∠B，以下三個命題中必有一個是正確的：（1）a=b，（2）ab.但a>b不可能為真，因為如果它成立，根據三角形中“大角對大邊”的定理，有∠A>∠B，與已知矛盾.同樣地，a

4.4 作底邊上的高

27種教材采用作底邊的高的方法.如圖13，給定△ABC，其中∠A=∠B.作CD⊥AB，那么在兩個直角△CAD和△CBD中∠A=∠B，所以∠ACD=∠BCD.因此，△CAD和△CBD中有兩個角及其夾邊CD對應相等，由ASA定理知△CAD≌△CBD，則AC=BC[12].

4.5 作頂角的平分線

11種教科書中采用作頂角平分線的方法.如圖13，在△ABC中∠A=∠B.作∠ACB的平分線CD，易證△CAD≌△CBD，故AC=BC[13].

4.6 作底角的平分線

有2種教科書采用作底角角平分線的方法.如圖14，給定△ABC，其中∠ABC=∠BAC.作BD平分∠ABC，AE平分∠BAC，由ASA定理知△DBA≌△EAB，從而∠BDA=∠AEB，所以∠CDB=∠CEA，且BD=AE，又∠C=∠C，故△ACE≌△BCD，故得AC=BC[14].

4.7 實驗操作法

3種教科書采用剪紙、折疊的方式來驗證“等角對等邊”，證明過程與“等邊對等角”的類似，這里不再贅述.

4.8 證明方法的演變

圖15給出了“等角對等邊”的各種證明在各時間段的分布情況.

由此可見，19世紀80年代之前“歐幾里得的反證法”占有絕對優勢，而后“作底邊的高證三角形全等”成為使用頻率最高的方法.歐幾里得的方法十分經典，只用到SAS定理，一度受到人們的青睞.但作底邊的高后無需分類討論，能通過一次三角形全等解決問題，相比之下證明過程更加簡便.“大邊對大角”“實驗操作”“想象有兩個三角形”和“作頂角的角平分線”等，都只是在少數幾個時間段內零星出現的方法.

奇怪的是，20世紀40年代涌現了一種新的方法，即“作底角的角平分線”證兩次三角形全等，從證明過程來看，該方法不如前面的大部分方法簡便，但它卻被20世紀40年代的教科書所采用.這看似較為復雜的證法，恰恰體現了數學家們不懈探究、追求創新的精神.

5 結論與啟示

“等邊對等角”與“等角對等邊”是歷史悠久的兩個命題，在兩千多年的歷史長河中，涌現了許多優秀的證明方法.這些證明方法相繼出現于本文所考察的103種早期幾何教科書中.遺憾的是，我們在今天的教科書中卻幾乎看不見它們的蹤影.美英早期幾何教科書中的證法各有特色，關于“等邊對等角”的證明，“萊斯利的方法”在各教科書中占絕對優勢.而關于“等角對等邊”的證明，“歐幾里得的反證法”在相當長的時期內都是主流方法，但到了19世紀80年代以后，“作底邊上的高”后來居上，而歐氏方法逐漸退出了歷史舞臺.

美英早期幾何教科書為HPM視角的等腰三角形教學提供了一定的啟示.

（1）營造探究之樂.本節內容可采用探究式學習的模式，設計不同大小等腰三角形的折紙活動，引導學生歸納出等腰三角形的性質.通過體驗性極強的折紙活動，學生能提高學習興趣，讓數學課堂活起來.接下來，教師則可以利用幾何畫板等現代工具對學生的猜想加以檢驗.在定理的證明上，先由學生自主探究其證明方法，再由教師進行講授，使學生充分參與到課堂中來.

（2）彰顯方法之美.無論是“等邊對等角”還是“等角對等邊”，早期教科書都呈現了豐富的證明方法.這些來自不同時空的靈活、多樣的方法，能夠拓寬學生的視野.教科書上呈現的一兩種推導方法是遠遠不夠的，教師應該對歷史上的多種證明方法進行介紹.而且，數學知識畢業后不用就很快遺忘了，但排除法、反證法等思想對學生來說卻是受益終身的.因此，教學不能僅局限于證明過程本身，更重要的是讓學生掌握證明背后蘊含的思想方法.

（3）實現能力之助.“等邊對等角”與“等角對等邊”互為逆命題，要判斷這兩個命題的真假必須分別對其進行嚴格的證明，這對于培養學生的邏輯推理能力有著極大的幫助.同時，課堂上安排折紙的實驗操作，也有利于學生直觀想象素養的發展.

（4）達成德育之效.一方面，教學過程中可以講述“驢橋”的故事，告訴同學們中世紀時期人們學習幾何也同樣會遇到挫折，讓學生們得到安慰，使數學變得不那么可怕.另一方面，通過折紙活動感知“等邊對等角”后進一步說明論證的安排，使學生明白數學是一門嚴密的學科，任何內容的學習不能僅停留在直觀.數學家們不懈探究、追求創新的治學態度，在早期幾何教科書對等腰三角形性質與判定定理的證明中體現得淋漓盡致.相信學生們通過本節內容的學習，能夠樹立正確的數學觀，培養理性精神.

參考文獻

[1]湯雪川，栗小妮，孫丹丹.“等腰三角形的性質”：從歷史中找應用，看證明[J].教育研究與評論（中學教育教學），2018（11）：52-61.

[2]楊虹霞，胡永強.問題驅動 以史為鑒 探究知識 解決問題——HPM視角下“等邊對等角”教學實錄與反思[J].上海中學數學，2020（12）：39-43.

[3]張青云.既見樹木，又見森林——對“等腰三角形的性質與判定”一課的設計與思考[J].中國數學教育（初中版），2019（11）：58-61.

[4]劉建.一次“單元教學”的實踐與思考——以“等腰三角形的性質與判定”為例[J].中學數學，2016（2）：30-32.

[5]唐小勃.談數學教材證明等邊對等角的方法不合理的原因[J].數學學習與研究，2018（8）：134-135.

[2]何紅英.從歐幾里得《幾何原本》談公理化思想[J].西安文理學院學報（自然科學版），2018，21（06）：11-13.

[3]Hunter T.Elements of Plane Geometry[M]. New York.： Harper & brothers， 1872.

[4]Halsted G B. The Elements of Geometry[M]. London： Macmillan， 1886.

[5]Legendre A M.Elements of Geometry [M]. Edinburgh： Oliver & Boyd， 1822.

[6]Leslie J S.Elements of Geometry [M]. Edinburgh： James Ballantyne and Co.， 1809.

[7]Wells W.The Essentials of Geometry （plane）[M]. Boston： D.C. Heath & Co.， 1901.

[8]Baker A. Elementary Plane Geometry [M]. Boston： Ginn &Company， 1903.

[9]Young J R.Elements of Geometry [M]. London： J. Souter， 1827.

[10]George W， Smith D E.Plane Geometry[M]. Boston： Ginn and Company， 1913.

[11]Slaught H E， Lennes N J. Plane Geometry [M]. Boston： Allyn and Bacon， 1918.

[12]Brooks E. Plane Geometry[M]. Philadelphia： Christopher Sower Company， 1901.

[13]Milne W J. Plane Geometry[M]. New York： American Book Company， 1899.

[14]Major G T.Plane Geometry[M]. Exeter： Edwards Brothers， 1946.

作者簡介 錢秦（1999—），女，重慶人，華東師范大學教師教育學院碩士研究生，主要從事數學史與數學教育研究.汪曉勤（1966—），男，浙江衢州人，教授，華東師范大學教師教育學院博士生導師，主要從事數學史與數學教育研究.