四元數(shù)聯(lián)合傳遞率在結(jié)構(gòu)狀態(tài)檢測中的應(yīng)用
任同群,鄭培珍,徐征,王曉東
(1.大連理工大學(xué)精密與特種加工教育部重點(diǎn)實(shí)驗(yàn)室,遼寧 大連116024;2.大連理工大學(xué) 微納米技術(shù)及系統(tǒng)遼寧省重點(diǎn)實(shí)驗(yàn)室,遼寧大連116024)
0 引言
在實(shí)際工程中,多數(shù)情況下結(jié)構(gòu)的激勵(lì)未知或不易測得,這導(dǎo)致無法準(zhǔn)確識(shí)別結(jié)構(gòu)的模態(tài)參數(shù),進(jìn)而限制了基于結(jié)構(gòu)參數(shù)變化的損傷檢測方法的應(yīng)用。相比之下,直接基于振動(dòng)響應(yīng)信號(hào)分析的狀態(tài)檢測方法不影響結(jié)構(gòu)正常運(yùn)行且費(fèi)用較低,已成為目前結(jié)構(gòu)健康檢測的研究熱點(diǎn),也得到了廣泛的工程應(yīng)用,其基本過程包括損傷特征提取與分類[1-4]。
在眾多所提取的損傷特征中,振動(dòng)傳遞率反映了結(jié)構(gòu)兩測點(diǎn)之間的全部力學(xué)特性,可表示為結(jié)構(gòu)剛度、阻尼和質(zhì)量等物理參數(shù)的函數(shù)。Fauziyah等人[5]利用加速度計(jì)陣列測量多泵間的振動(dòng)傳遞率,實(shí)現(xiàn)了多泵的故障診斷。Dong等人[6]基于振動(dòng)傳遞率對隨機(jī)激勵(lì)下的螺栓松動(dòng)監(jiān)測進(jìn)行了研究,克服了常用的振動(dòng)方法在發(fā)現(xiàn)螺栓局部松動(dòng)方面的不足。楊斌[7]采用相空間重構(gòu)方法進(jìn)行振動(dòng)傳遞率函數(shù)分析,重構(gòu)振動(dòng)傳遞率函數(shù)矩陣,并以其奇異值熵作為損傷指標(biāo),提高了檢測方法的抗干擾性。Luo等人[8]以加權(quán)傳遞率作為損傷指標(biāo)評(píng)估結(jié)構(gòu)狀態(tài),提高了TF的信噪比。Chen等人[9]利用神經(jīng)網(wǎng)絡(luò),提取基于振動(dòng)傳遞率的損傷診斷指標(biāo),并驗(yàn)證了其正確性。
在上述研究中,振動(dòng)傳遞率僅基于單通道信號(hào)計(jì)算獲得。在工程應(yīng)用中,測試信號(hào)是實(shí)際振動(dòng)在傳感器敏感方向的投影。因此,基于單通道信號(hào)的方法在處理空間振動(dòng)問題時(shí)容易陷入困難。為解決此問題,通常采用多加速度計(jì)或三軸加速度計(jì)獲取空間振動(dòng)信號(hào),進(jìn)行單通道信號(hào)處理及特征提取后再進(jìn)行特征融合。但是,這種處理方法忽略了信號(hào)通道之間的關(guān)聯(lián)性,融合后會(huì)帶來失真甚至是虛假的結(jié)果。因此,有必要將多通道信號(hào)視為矢量信號(hào),進(jìn)行同時(shí)處理,以保證通道間的關(guān)聯(lián)性。四元數(shù)三個(gè)虛部的運(yùn)算是等價(jià)的,因此非常適合表示三維矢量信號(hào)。例如,Rehman和Mandic[10]研究了三維信號(hào)的經(jīng)驗(yàn)?zāi)B(tài)分解,并證明三通道信息聯(lián)合處理時(shí)會(huì)獲得更好的精度。Tong[11]采用四元數(shù)K-LT對故障異步電機(jī)進(jìn)行特征提取,但處理的數(shù)據(jù)僅限于時(shí)域四元數(shù)振動(dòng)序列。Yi和Lv等人[12-13]描述了四通道信號(hào)的相關(guān)性,提出一種基于凸優(yōu)化的四元數(shù)奇異譜分析方法。Ren等人[14-15]采用四元數(shù),構(gòu)建三軸信號(hào)的振動(dòng)傳遞率,并驗(yàn)證了K-LT法和DQWT法,取得了較好的結(jié)果。此外,Ell和Sangwine[16-19]針對四元數(shù)傅立葉變換和相關(guān)分析問題進(jìn)行了合作研究,相關(guān)研究成果為四元數(shù)頻域分析奠定了理論基礎(chǔ)。
本文提出了一種基于QTJT的狀態(tài)檢測方法,先后采用K-LT和DQWT技術(shù)提取狀態(tài)特征指標(biāo)向量,然后定義狀態(tài)特征指標(biāo)向量之間的歐氏距離并將其作為狀態(tài)指標(biāo),針對軌道結(jié)構(gòu)扣件松脫及內(nèi)部溫度力的變化,進(jìn)行了狀態(tài)檢測與識(shí)別。通過在無砟軌道試驗(yàn)平臺(tái)上開展實(shí)際實(shí)驗(yàn),驗(yàn)證該方法的有效性。
1 四元數(shù)聯(lián)合傳遞率相關(guān)理論
1.1 四元數(shù)傳遞率計(jì)算
對于單通道信號(hào),振動(dòng)傳遞率定義為結(jié)構(gòu)兩測試點(diǎn)的時(shí)域序列xi(輸出)和xj(輸入)的頻譜比值。它描述了振動(dòng)(振幅和相位)如何在結(jié)構(gòu)的兩個(gè)測試點(diǎn)之間進(jìn)行傳遞。假設(shè)一個(gè)n自由度線性結(jié)構(gòu)受外力f(t)=[f1(t),f2(t),…,fn(t)]的激勵(lì),如果f(t)具有形如白噪聲的均勻譜密度,則fk(t),k=1,2,…,n的傅立葉變換則為一個(gè)常數(shù)D。此時(shí),由節(jié)點(diǎn)j到i的振動(dòng)傳遞率計(jì)算公式為
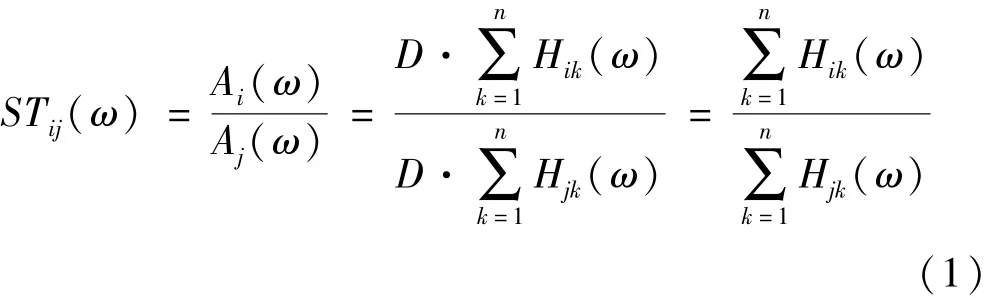
式中:Ai(w),Aj(w)分別為節(jié)點(diǎn)i,j處振動(dòng)加速度信號(hào)的頻譜;H(ω)為n×n的頻響函數(shù)矩陣,H(ω)=-(ω2M+iωC+K)-1;M為n×n的質(zhì)量矩陣;C為n×n的阻尼矩陣;K為n×n的剛度矩陣。如果激振力只作用于一點(diǎn)k,式(1)變?yōu)?/p>
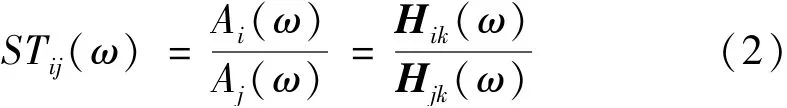
上述兩情形中,激振力僅提供了振動(dòng)能量,并未參與傳遞率的計(jì)算。此時(shí),振動(dòng)傳遞率僅與激勵(lì)位置有關(guān)。根據(jù)式(1)和式(2),振動(dòng)傳遞率與頻響函數(shù)有關(guān),反映了結(jié)構(gòu)的內(nèi)在特性。因此,振動(dòng)傳遞率可以用于結(jié)構(gòu)狀態(tài)檢測。
采用三軸加速度計(jì)采集獲得結(jié)構(gòu)三個(gè)正交方向的振動(dòng)信號(hào)ax(t),ay(t),az(t),可以構(gòu)建純虛四元數(shù)的時(shí)域序列aq(t)=[aq1,aq2,…,aqM],其中,aqr=iaxr+jayr+kazr,r∈[1,2,…,M],M為序列維度。此時(shí),傳統(tǒng)的基于單通道信號(hào)頻譜之比的振動(dòng)傳遞率不再適用。此時(shí)四元數(shù)傳遞率可定義為
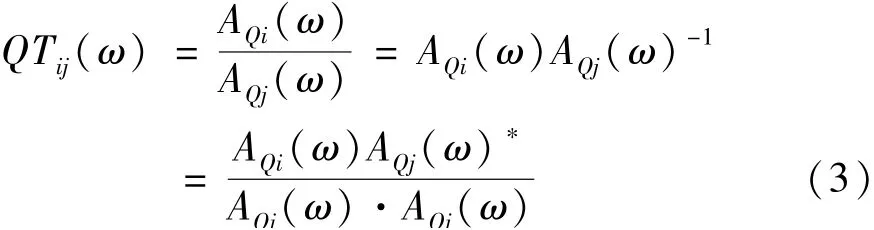
式中:AQ(ω)為四元數(shù)譜;·為四元數(shù)點(diǎn)乘符號(hào);?為共軛運(yùn)算符號(hào)。
Ell提出了四元數(shù)傅立葉變換用于分析二維線性定常系統(tǒng)[16-17],其原始定義可表示為
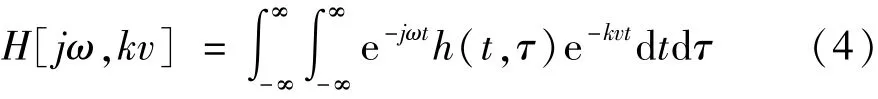
式(4)定義了二維函數(shù)h(t,τ)從空間域(t,τ)向空間頻域(jω,kv)的轉(zhuǎn)換。四元數(shù)傅立葉變換最早用于彩色圖像的分析,具體形式[18]如下
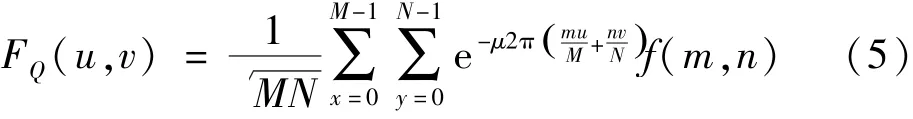
式中:μ為隨機(jī)單位純虛四元數(shù);f(m,n)為M×N彩色圖像矩陣(三顏色通道構(gòu)建純虛四元數(shù));(m,n)和(u,v)分別為空間域和空間頻域的坐標(biāo)。對于純虛四元數(shù)振動(dòng)時(shí)域序列aq(t),可視其為1×N的彩色圖像,因此,aq(t)的四元數(shù)譜計(jì)算公式為
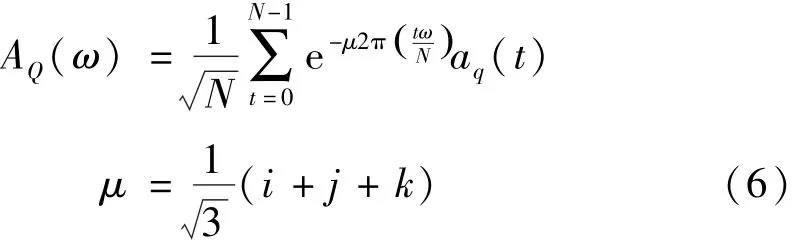
由式(6)可知,AQ(ω)也是四元數(shù)序列,故由頻譜之比定義的四元數(shù)傳遞率也是在頻域內(nèi)的四元數(shù)序列,和普通傳遞率一樣,也包含了全部的結(jié)構(gòu)內(nèi)在特性。
1.2 四元數(shù)傳遞率特性
參考實(shí)數(shù)信號(hào)的傅立葉變換,四元數(shù)時(shí)域序列亦可以由不同頻率分量的四元數(shù)信號(hào)的線性組合來表示。類似地,在四元數(shù)傅立葉變換中,可將變換后的模值作為縱坐標(biāo)得到四元數(shù)幅頻譜。
不失一般性,構(gòu)造如下三通道信號(hào)[x(t),y(t),z(t)],三個(gè)通道分別由不同頻率的正(余)弦信號(hào)組成
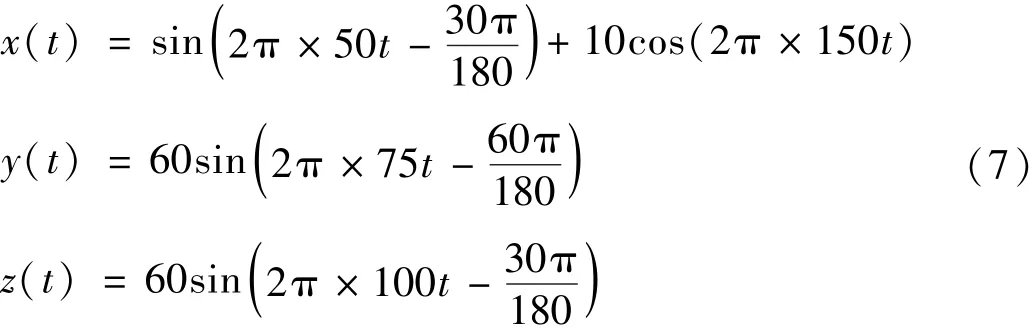
對x(t),y(t),z(t)三個(gè)單通道信號(hào)分別進(jìn)行獨(dú)立的傅立葉變換,得到幅值譜如圖1(a)所示,然后將三個(gè)通道信號(hào)聯(lián)合成[x(t),y(t),z(t)],構(gòu)建四元數(shù)序列并進(jìn)行四元數(shù)傅立葉變換,可得到整體的頻域信息,其幅值譜如圖1(b)所示。對比可以發(fā)現(xiàn),聯(lián)合信號(hào)的四元數(shù)頻譜包含了全部信號(hào)的頻率成分,是三通道信息的無損融合[20]。
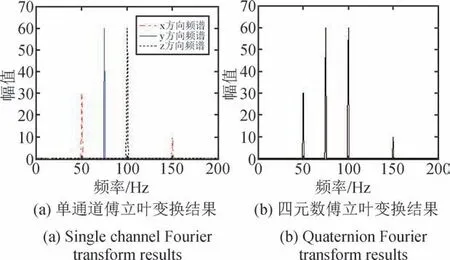
圖1 四元數(shù)傅立葉變換Fig.1 Quaternion Fourier transform of three-channel joint signal
當(dāng)振動(dòng)方向偏離傳感器的敏感方向且僅使用單軸傳感器時(shí),振動(dòng)幅值會(huì)減小,但頻率不變。如果傳感器的安裝方向不能嚴(yán)格一致,傳統(tǒng)的基于單通道信號(hào)的振動(dòng)傳遞率將偏離理論值。在實(shí)際工程應(yīng)用中,很難保證檢測時(shí)傳感器的安裝方向嚴(yán)格一致。不僅如此,若振動(dòng)方向是時(shí)變的,將直接導(dǎo)致傳遞率的時(shí)變,進(jìn)而造成結(jié)構(gòu)狀態(tài)的誤診斷。
圖2 (a)描述了任意向量v∈R3繞3D單位向量u旋轉(zhuǎn)2θ的情形。用上節(jié)中的定義將向量u和v擴(kuò)展為純虛四元數(shù),則旋轉(zhuǎn)之后得到的向量v′計(jì)算公式為

式中:euθ為單位四元數(shù)的指數(shù)形式,euθ=cosθ+usinθ。式(8)等價(jià)于三軸加速度計(jì)的測量坐標(biāo)系原點(diǎn)不變,坐標(biāo)系的方向繞向量u旋轉(zhuǎn)2θ,如圖2(b)所示。
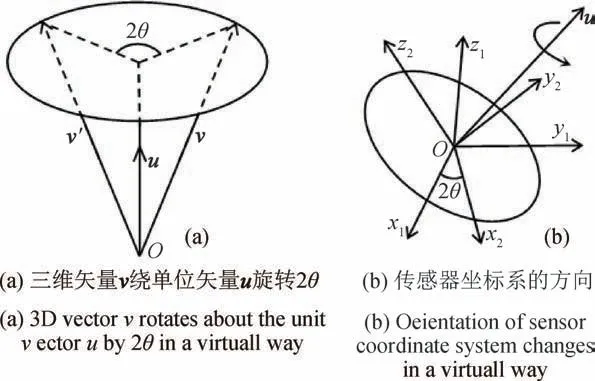
圖2 四元數(shù)描述空間向量旋轉(zhuǎn)Fig.2 Quaternion describes vector rotation in space
向量v′的模值計(jì)算公式為
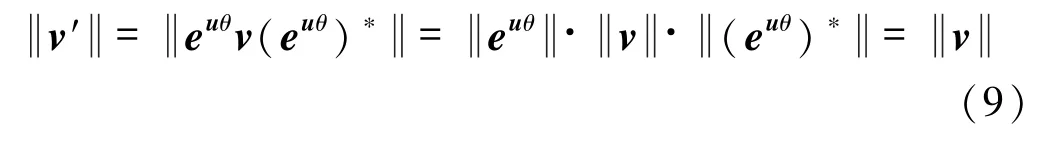
上述分析表明當(dāng)采用三軸加速度計(jì)時(shí),只要安裝位置固定,無論其安裝姿態(tài)如何變化,均可如實(shí)采集獲得空間振動(dòng)信號(hào)。進(jìn)而可推論,兩測點(diǎn)的三軸加速度計(jì)位置固定且不考慮噪聲干擾時(shí),不論安裝姿態(tài)如何,式(3)的四元數(shù)傳遞率幅值均為其理論值。為證明上述推論,基于無砟軌道綜合試驗(yàn)平臺(tái),獲得兩測點(diǎn)振動(dòng)信號(hào)的四元數(shù)時(shí)域序列,通過理論計(jì)算將測點(diǎn)A,B的信號(hào)分別繞u1,u2旋轉(zhuǎn)π/6和π/3,獲得三組四元數(shù)振動(dòng)傳遞率,即初原始、僅旋轉(zhuǎn)A信號(hào)以及旋轉(zhuǎn)A/B信號(hào)的四元數(shù)振動(dòng)傳遞率,如圖3所示。由圖3可知,當(dāng)傳感器姿態(tài)發(fā)生變化時(shí),四元數(shù)傳遞率的實(shí)部與虛部幅值均發(fā)生變化,但整體幅值不變。其中,u1,u2分別為
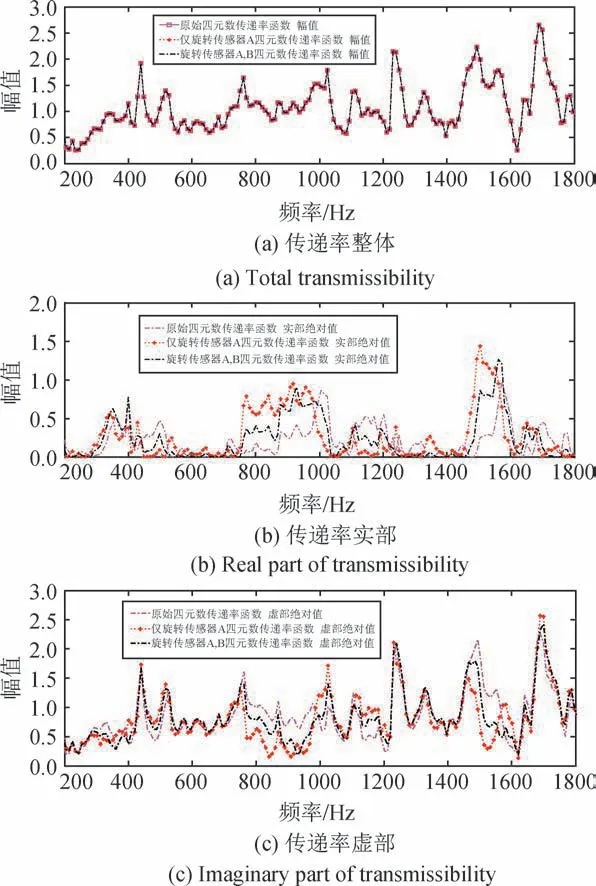
圖3 信號(hào)旋轉(zhuǎn)前后的四元數(shù)傳遞率幅值Fig.3 Amplitude of quaternion transmissibility before and after signal rotation
1.3 對偶樹四元數(shù)小波變換
對偶樹小波變換由離散小波變換(discrete wavelet transform,DWT)和復(fù)小波變換(complex wavelet transform,CWT)拓展而來,基于二維解析信號(hào)和希爾伯特變換(Hilbert transform,HT)構(gòu)造而成。與實(shí)小波變換相比,對偶樹四元數(shù)小波變換可以獲得多角度、多尺度下的一個(gè)幅值和三個(gè)相位信息,同時(shí)具有良好的時(shí)移不變性[21]。
為了推廣到二維,Bülow[22]根據(jù)四元數(shù)傅里葉變換給出了四元數(shù)解析信號(hào)的定義,給定一個(gè)實(shí)數(shù)二維信號(hào)f(x,y),其四元數(shù)解析信號(hào)定義為
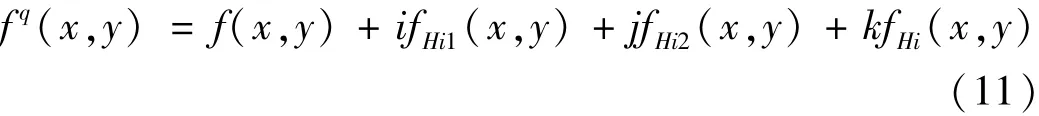
式中:fHi1(x,y)和fHi2(x,y)分別為沿x和y軸的希爾伯特變換;fHi(x,y)為完整的希爾伯特變換。
二維離散小波變換由一維離散小波變換沿兩個(gè)正交基的張量積構(gòu)成,可表示為尺度函數(shù)φ(x)φ(y)、水平方向子帶函數(shù)φ(x)ψ(y)、豎直方向子帶函數(shù)ψ(x)φ(y)和對角線方向子帶函數(shù)ψ(x)ψ(y)的組合[23]。相似地,四元數(shù)小波同樣具有一個(gè)尺度函數(shù)和三個(gè)小波子帶函數(shù),即將二維離散小波變換與三個(gè)實(shí)小波(由一維希爾伯特變換得到)組合構(gòu)成一個(gè)四元數(shù),從而得到二維解析小波。以對角子帶ψ(x)ψ(y)為例,其二維希爾伯特變換計(jì)算公式為
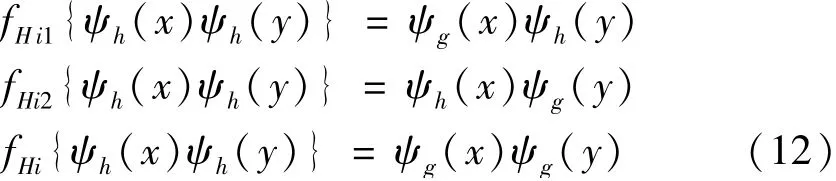
式中:(ψh,ψg)為特定濾波器h和g對應(yīng)的小波函數(shù),它遵循{ψh,ψg=HT(ψh)}的原則。式(12)中的每個(gè)分量均可由一維對偶樹復(fù)小波的組合計(jì)算。因此,對角線子帶四元數(shù)小波計(jì)算公式為
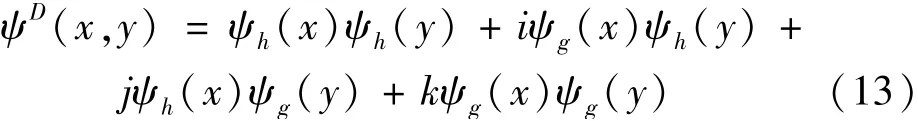
同理可得水平、垂直子帶四元數(shù)小波以及四元數(shù)尺度函數(shù)[24]分別為
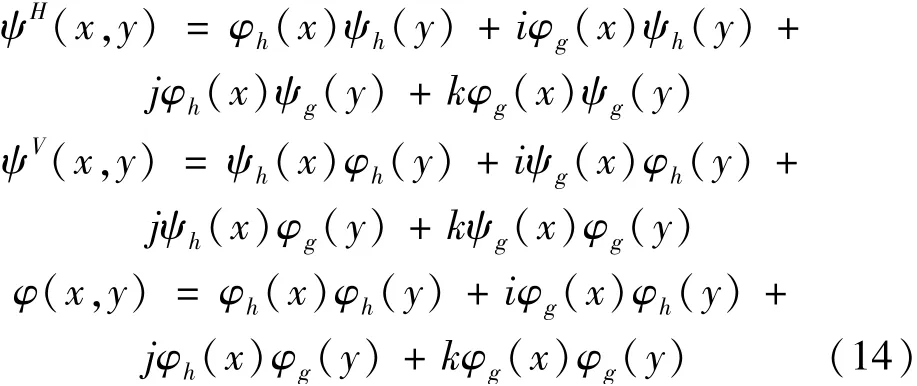
對偶樹小波變換的計(jì)算細(xì)節(jié)可參考文獻(xiàn)[25]。
2 基于四元數(shù)聯(lián)合傳遞率的狀態(tài)檢測方法
2.1 卡洛變換(K-LT)法
K-LT是一種基于對象統(tǒng)計(jì)特征的最優(yōu)正交變換。它可以消除統(tǒng)計(jì)相關(guān)性,但保留分類信息。將狀態(tài)已知條件下測量得到的四元數(shù)傳遞率模值向量作為訓(xùn)練樣本,并構(gòu)建為狀態(tài)矩陣SQ=[s1,s2,…,sN]∈RM×N,其中M為測量四元數(shù)傳遞率的長度,即參與運(yùn)算的有效譜線數(shù)目,N為測量的傳遞率數(shù)目。狀態(tài)矩陣SQ的協(xié)方差矩陣CQ∈RM×N可以分解為
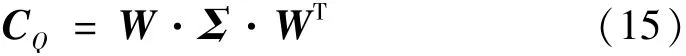
式中:W=[w1,w2,…,wN]∈RM×N為特征向量矩陣張成的特征子空間;Σ=diag(λ1,λ2,…,λN)∈RN×N為特征值矩陣,且λ1≥λ2≥…≥λN。對任意訓(xùn)練四元數(shù)傳遞率模值向量sj,j=1,2,…,N,將其投影到特征子空間可獲得新的向量sj′=WT·sj。此時(shí),s′j可作為狀態(tài)索引向量。將未知狀態(tài)下測得的四元數(shù)傳遞率模值向量以同樣方式投影到特征子空間,獲得投影向量s′t,然后計(jì)算s′j和s′t的歐氏距離,稱取得最小歐式距離的投影向量為匹配向量,即同一狀態(tài)。
2.2 對偶樹四元數(shù)小波變換(DQWT)法
如圖4所示,將同一狀態(tài)下4個(gè)測試四元數(shù)傳遞率模值向量疊加,構(gòu)建狀態(tài)特征圖。圖4表明同一狀態(tài)下的不同樣本有很大的相似性而又有著局部的差異性。

圖4 四元數(shù)傳遞率灰度圖Fig.4 Grey-scale map of quaternion transmissibility
對狀態(tài)特征圖進(jìn)行對偶樹小波變換,其系數(shù)可構(gòu)成一個(gè)矩陣F,即
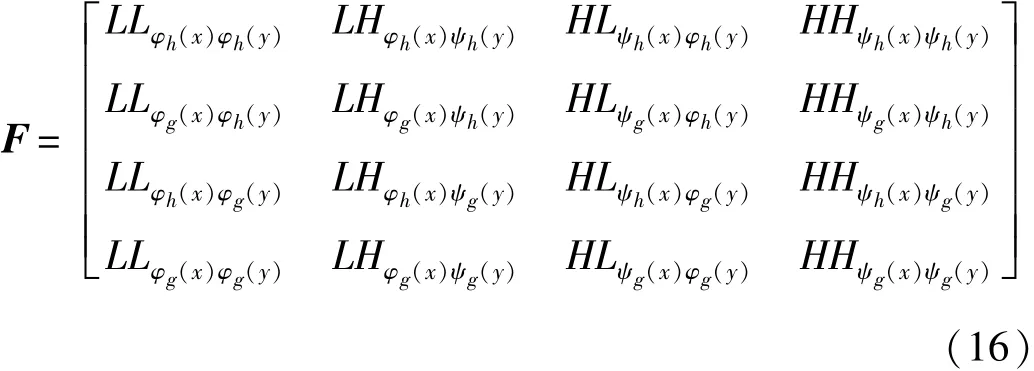
F的第一列包含圖像的低頻信息,第2~4列分別代表圖像在水平方向、垂直方向和對角線方向的高頻信息。
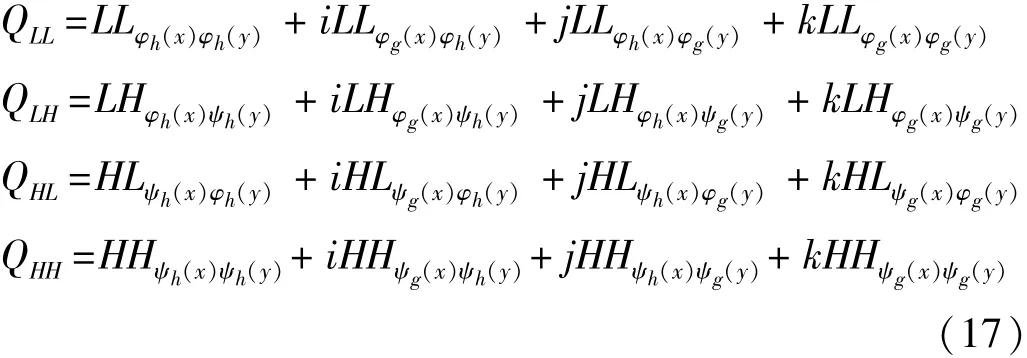
對偶樹小波變換的系數(shù)包含了一個(gè)幅值信息和三個(gè)相位信息。F的每一列可以構(gòu)成式(17)的四元數(shù),計(jì)算其每個(gè)四元數(shù)的幅值和相位,并重新組合得到幅值-相位矩陣

獲得每種已知狀態(tài)下的多組四元數(shù)傳遞率,構(gòu)建狀態(tài)特征圖作為訓(xùn)練樣本,對其進(jìn)行對偶樹四元數(shù)小波變換得到低頻幅值相位向量AFi,同樣地,構(gòu)建未知狀態(tài)下的狀態(tài)特征圖,計(jì)算其低頻幅值相位向量AFj,計(jì)算AFi和AFj之間的最小歐式距離并將其作為狀態(tài)識(shí)別指標(biāo),與上節(jié)方法類似。取低頻幅值相位信息,既綜合考慮了二維傳遞率圖像的幅值相位信息,又減小了單傳遞率的測量不確定性對檢測結(jié)果的影響,且降低了原始數(shù)據(jù)的大小。
3 狀態(tài)檢測實(shí)驗(yàn)
實(shí)驗(yàn)對象為總長20 m的CRTS-I型“無砟軌道綜合試驗(yàn)平臺(tái)”,鋼軌兩端鎖緊,中間由配套的WJ-7型扣件鎖緊。實(shí)驗(yàn)時(shí)在軌底隔跨兩組扣件安裝兩個(gè)三軸加速度傳感器PCB 356A33,采用力錘YD-5T在實(shí)驗(yàn)區(qū)域左側(cè)某處的軌頂施加激勵(lì),敲擊方向垂直于軌頂并保持激勵(lì)位置固定,以10 kHz的采樣頻率采集振動(dòng)信號(hào),采集設(shè)備為DHDAS-5902動(dòng)態(tài)信號(hào)采集分析系統(tǒng)。實(shí)驗(yàn)現(xiàn)場及傳感器布置如圖5所示。
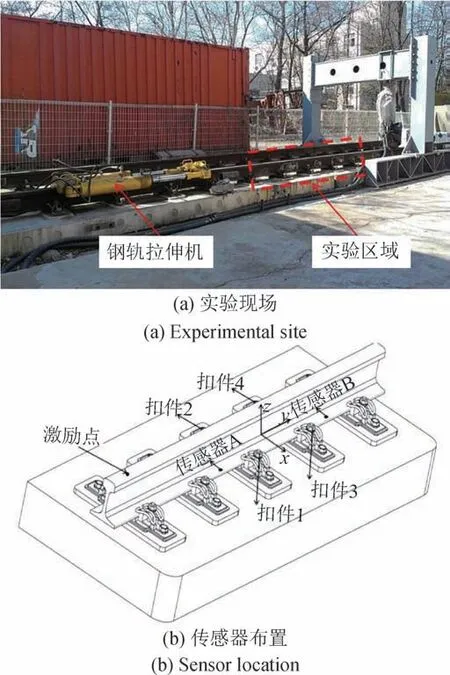
圖5 實(shí)驗(yàn)現(xiàn)場及傳感器布置Fig.5 Experiment site and sensor location
首先,利用鋼軌扣件的松脫與否模擬不同狀態(tài),根據(jù)扣件松脫順序設(shè)置五種不同工況,分別為:扣件全部鎖緊,扣件1松脫,扣件1和2松脫,扣件1,2和3松脫以及4個(gè)扣件全部松脫。每種工況下,在左側(cè)激勵(lì)點(diǎn)用力錘激勵(lì)40次。根據(jù)前述四元數(shù)傳遞率函數(shù)的計(jì)算方法,計(jì)算得到每種工況下的40組傳遞率函數(shù)。圖6為工況1下的全部40次四元數(shù)傳遞率,取200~1700 Hz部分傳遞率函數(shù),可見其重合性很好[26]。一方面,說明了傳遞率計(jì)算的正確性;另一方面,也驗(yàn)證了四元數(shù)傳遞率函數(shù)僅由激勵(lì)位置和結(jié)構(gòu)自身特性確定,而與激勵(lì)大小無關(guān)的結(jié)論。
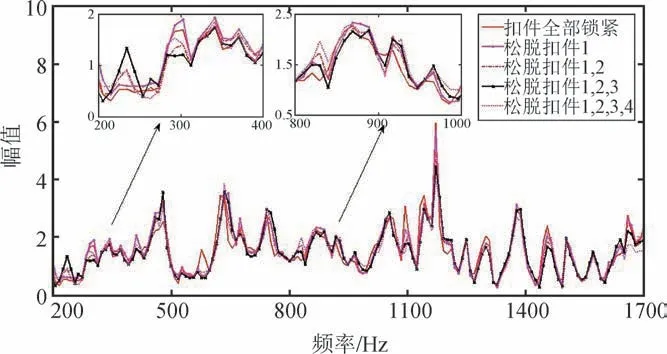
圖6 工況1下40組原始四元數(shù)傳遞率函數(shù)幅值譜[26]Fig.6 Amplitude spectrums of 40 sets of original quaternion transmissibility under situation 1[26]
分別求取五種工況下的40組四元數(shù)傳遞率函數(shù)平均值,如圖7所示。在選取頻段內(nèi),傳遞率譜線大體重合,僅在部分頻率區(qū)間存在較明顯差別。這是因?yàn)橄噍^實(shí)驗(yàn)區(qū)域,試驗(yàn)平臺(tái)在較長一段鋼軌上的扣件是鎖緊的,僅松脫局部相鄰扣件對整體結(jié)構(gòu)的影響較小。
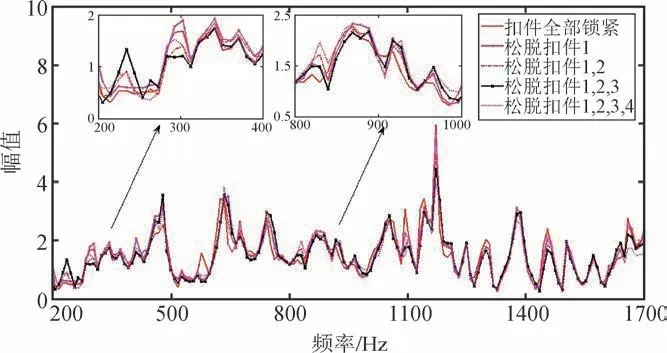
圖7 五種工況下平均四元數(shù)傳遞率函數(shù)幅值譜Fig.7 Average amplitude spectrum of quaternion transmissibility under five situations
采用2.1中基于K-LT的方法進(jìn)行狀態(tài)識(shí)別,分別取五種工況的前30組傳遞率函數(shù)作為訓(xùn)練樣本,后10組作為測試樣本,用來驗(yàn)證該方法的有效性。檢測結(jié)果如表1所示,其中,測試QTJT(i)下的第一列數(shù)字表示與之取得最小歐氏距離的訓(xùn)練樣本列序號(hào),正確識(shí)別時(shí)第j測試組下的QTJT(i)對應(yīng)序號(hào)應(yīng)為30×(j-1)+1~30j;第二列表示狀態(tài)識(shí)別結(jié)果,‘√’表示識(shí)別正確,‘×’表示識(shí)別錯(cuò)誤。由表1可知,該方法取得了98%的狀態(tài)識(shí)別正確率。
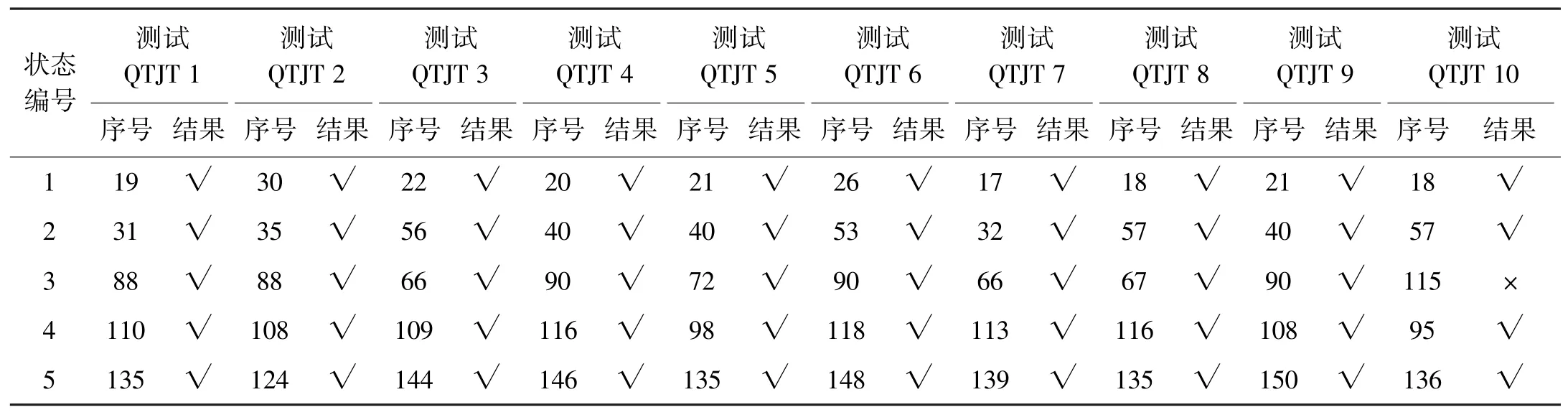
表1 基于K-LT方法扣件松脫狀態(tài)檢測結(jié)果[26]Tab.1 Detection results based on K-LT method
基于上述數(shù)據(jù),采用2.2中DQWT方法進(jìn)行狀態(tài)識(shí)別處理,分解層次取2,每種狀態(tài)下計(jì)算得到的40組QTJTs模值矩陣V∈R152×40,每4組QTJT作為一個(gè)樣本,每種狀態(tài)得到10組樣本,其中前6組作為訓(xùn)練樣本,后4組作為測試樣本。識(shí)別結(jié)果如表2所示,狀態(tài)i(i=1,2,3,4,5)正確的匹配范圍應(yīng)為6(i-1)+1~6i。由表2可知,該方法狀態(tài)識(shí)別正確率達(dá)到了100%。
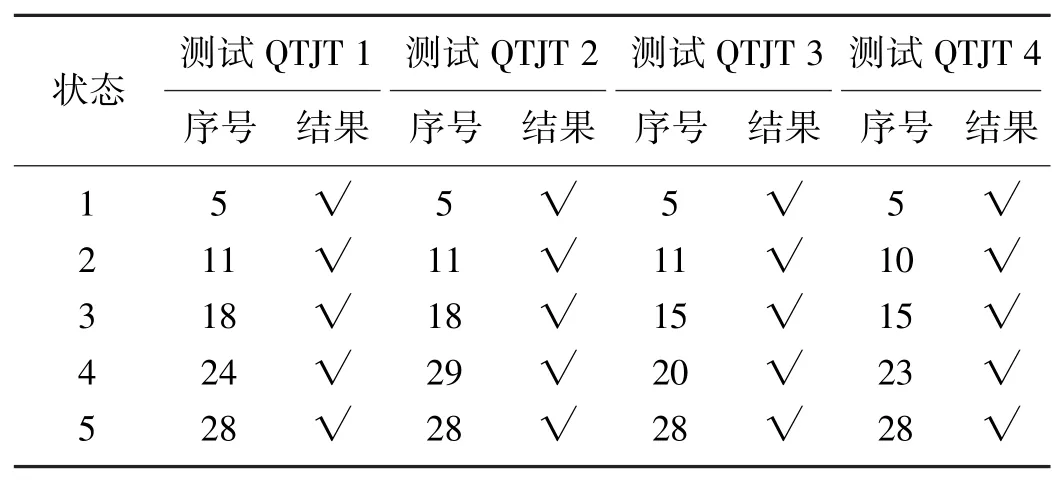
表2 基于DQWT方法扣件松脫狀態(tài)檢測結(jié)果[26]Tab.2 Detection results based on DQWT method
采用LG-900型液壓鋼軌拉伸機(jī)拉伸鋼軌,模擬鋼軌內(nèi)部縱向溫度力的變化,分別設(shè)置拉應(yīng)力:0,10,20,30,40,50 MPa。首先,松脫全部扣件以釋放鋼軌內(nèi)部縱向溫度力,穩(wěn)定后拉伸機(jī)分別以上述設(shè)置應(yīng)力動(dòng)作進(jìn)行鋼軌拉伸,而后再將全部扣件鎖緊,縮緊力矩為150 N·m。同樣地,每次拉伸之后按照前面的實(shí)驗(yàn)方法,依次松脫相鄰兩組扣件,得到30組狀態(tài),每種狀態(tài)采集20組振動(dòng)信號(hào),計(jì)算得到20組四元數(shù)傳遞率。在每種狀態(tài)下,以其前12組QTJT分別構(gòu)建3個(gè)狀態(tài)特征圖作為訓(xùn)練樣本,以后8組QTJT分別構(gòu)建2個(gè)狀態(tài)特征圖作為測試樣本,表3為該實(shí)驗(yàn)的狀態(tài)組織安排情況。基于DQWT方法進(jìn)行狀態(tài)識(shí)別處理,每種狀態(tài)的匹配范圍應(yīng)為3(i-1)+1~3i,所有樣本的識(shí)別結(jié)果如表4所示,該方法狀態(tài)識(shí)別正確率達(dá)到了100%。
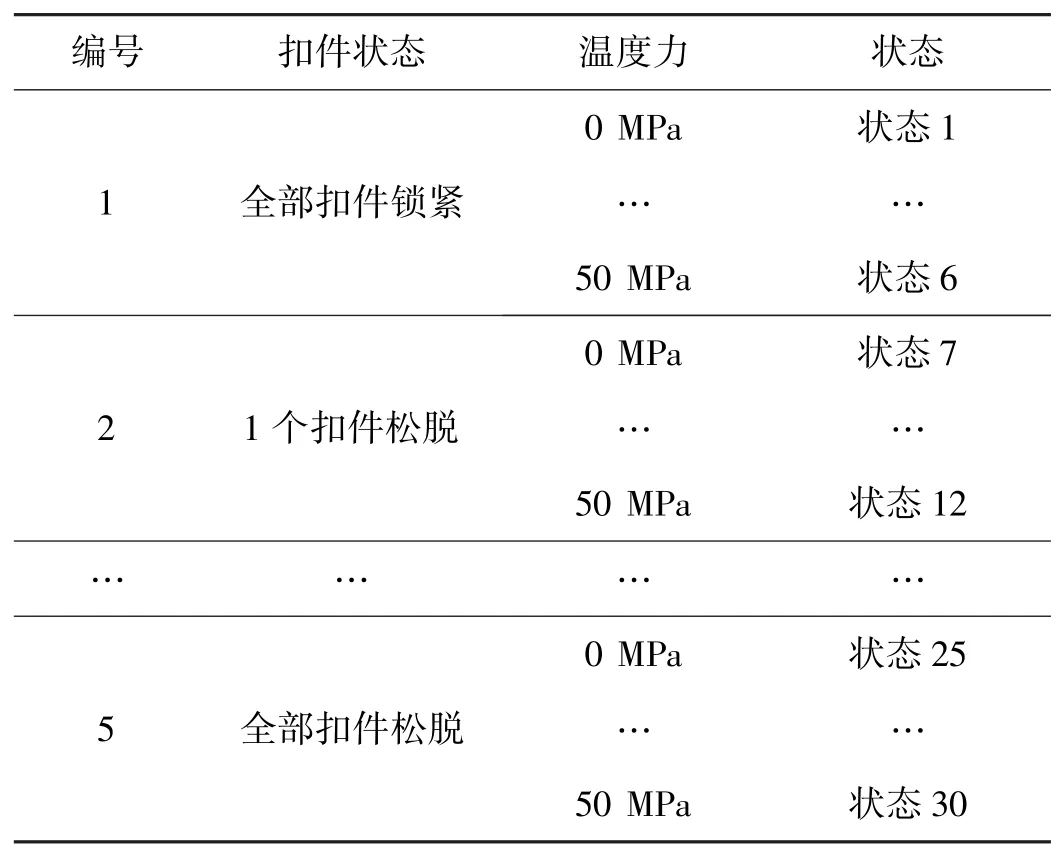
表3 溫度力、扣件松脫綜合實(shí)驗(yàn)結(jié)構(gòu)狀態(tài)安排Tab.3 Structure state arrangement for comprehensive experiment of temperature force and fastener looseness
表4 的實(shí)驗(yàn)結(jié)論表明,該方法可實(shí)現(xiàn)分辨力優(yōu)于10 MPa的鋼軌溫度力變化識(shí)別。基于鐵路軌道相關(guān)標(biāo)準(zhǔn),鋼軌的相關(guān)參數(shù)如下:截面積為7.745×10-3m2,線膨脹系數(shù)α=0.0118 mm/(m·℃),彈性模量E=2.1×105 MPa。則軌溫有1℃變化時(shí)所產(chǎn)生的內(nèi)部縱向力計(jì)算公式為
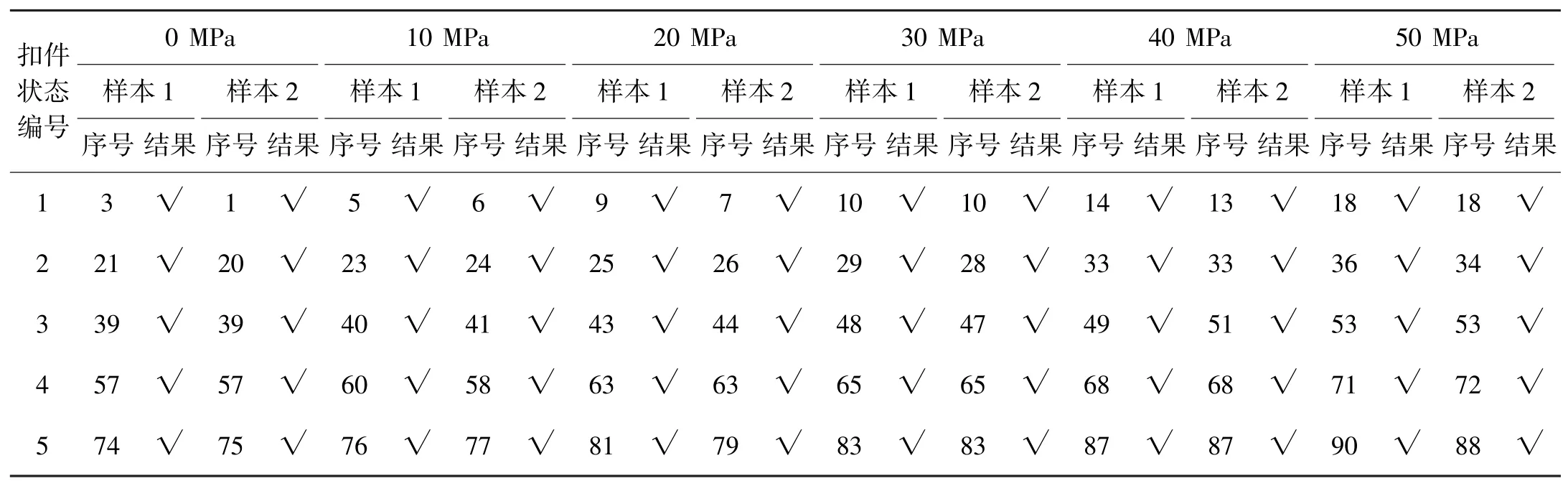
表4 基于DQWT溫度力、扣件松脫綜合鋼軌狀態(tài)檢測結(jié)果[26]Tab.4 Detection results based on DQWT method for the comprehensive experiment
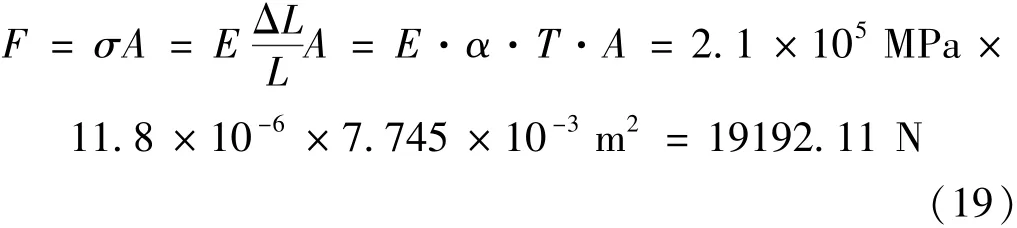
LG-900型液壓鋼軌拉伸機(jī)的油缸截面積為S=3.352×10-3m2,則其10 MPa的拉應(yīng)力對應(yīng)10 MPa×S=33520 N的拉力。進(jìn)而,10 MPa的拉應(yīng)力相對應(yīng)的鋼軌溫度變化為33520 N/19192.11 N×1℃=1.75℃。因此,本方法可實(shí)現(xiàn)分辨力優(yōu)于10 MPa的鋼軌溫度力變化識(shí)別,相當(dāng)于鎖定狀態(tài)下1.75℃的軌溫變化。
4 結(jié)論
將傳統(tǒng)的基于單通道信號(hào)的振動(dòng)傳遞率推廣到多通道信號(hào)的四元數(shù)振動(dòng)傳遞率,并結(jié)合K-LT技術(shù)和DQWT,給出了基于四元數(shù)聯(lián)合傳遞率的的結(jié)構(gòu)狀態(tài)檢測方法。通過在無砟軌道試驗(yàn)平臺(tái)上的實(shí)際試驗(yàn),驗(yàn)證了該方法的有效性,狀態(tài)識(shí)別結(jié)果正確率高于95%。上述方法提供了一種識(shí)別狀態(tài)變化是否存在的解決方案,未來可以通過增加測試點(diǎn)和依次識(shí)別相鄰四元數(shù)傳遞率,進(jìn)一步發(fā)展為同時(shí)識(shí)別狀態(tài)變化的存在和位置。更重要的是,該方法保留了振動(dòng)傳遞率的理論值,對傳感器的安裝方向沒有嚴(yán)格的要求,在實(shí)際應(yīng)用中具有明顯優(yōu)勢。特別是基于DQWT的方法,綜合考慮了多個(gè)被測傳遞率,降低了單次測量不確定性的影響。本文的研究為推動(dòng)直接基于振動(dòng)響應(yīng)信號(hào)分析的狀態(tài)檢測方法發(fā)展起到了積極作用,具有重要技術(shù)應(yīng)用價(jià)值。

