太陽輻射對環火段通信鏈路的影響分析及參數設計

孫文 ，閆毅，范亞楠 ，姚秀娟，高翔，閆文康

1. 中國科學院 國家空間科學中心，北京 100190 2. 中國科學院大學，北京 100049

1 引言

在深空探測過程中，太陽會對航天器、通信鏈路產生各種影響[1-5]。太陽對鏈路的最大的影響發生在上合階段，此時太陽對于鏈路的影響有太陽閃爍效應和太陽輻射導致接收天線噪聲溫度上升兩種[1]，本文主要討論太陽輻射對傳輸鏈路的影響。上合階段太陽強大的輻射能量直接被地面站天線接收，從而導致相對較弱的傳輸信號被淹沒[4]，造成地面站天線接收系統的等效噪聲溫度增大，進而導致天線接收系統載噪比惡化，引起鏈路通信質量嚴重下降甚至中斷[5]。因此，分析深空探測過程中的太陽輻射對地面站的影響對實現探測器的追蹤監測、判斷深空探測中鏈路是否可用及保障接收數據的可靠性有至關重要的作用。

國內外對于深空通信上合階段太陽輻射對鏈路影響的研究大多都基于實測數據的曲線擬合[4-7],在擬合曲線的基礎上分析了上合階段地面站接收到的太陽輻射噪聲溫度，但均未在理論上給出太陽噪聲溫度的計算方法。文獻[7]分析了春分、秋分時期，太陽輻射對同步軌道衛星鏈路的影響。文獻[8]利用DSS13的34 m波束波導天線和Ka波段單脈沖接收系統進行太陽輻射噪溫試驗，繪制出不同∠SEP下地面站噪聲溫度的曲線圖。文獻[9]研究了月亮等黑體輻射對地面站接收天線造成的噪聲溫度,指出天線噪聲溫度等于天線增益和熱體亮溫度的加權平均值；文獻[10]研究了太陽輻射對地面站天線的影響，但是沒有具體到頻率和天線口徑等具體參數。

本文以深空探測中的火星探測為例，對太陽輻射對鏈路的影響展開具體分析。首先對環火段地面站-太陽-探測器之間軌道關系進行數學建模分析，總結了太陽-地面站-探測器夾角∠SEP隨時間的變化規律。基于環火段軌道數學模型，分析了上合階段太陽對地面站接收噪聲溫度的影響，給出了太陽噪聲溫度與∠SEP、頻率、天線口徑之間的關系，并給出太陽噪聲溫度的具體計算方法；總結了地面站天線受到太陽輻射干擾的嚴重程度、干擾時間與頻率、天線口徑、角度之間的關系；給出環火段通信鏈路參數的設計建議，為以后深空探測系統中太陽影響下星際通信鏈路參數的選取提供了一定的參考意見。

2 環火段軌道建模及角度分析

火星探測軌道過程分為轉移段和環火段，文獻[11]完成了最優轉移軌道設計。在環火段，探測器到火星之間的距離遠小于火星到地球的距離，因此分析時把探測器看成火星的一部分。探測器、地球、太陽之間的軌道關系和角度變化如圖1所示。

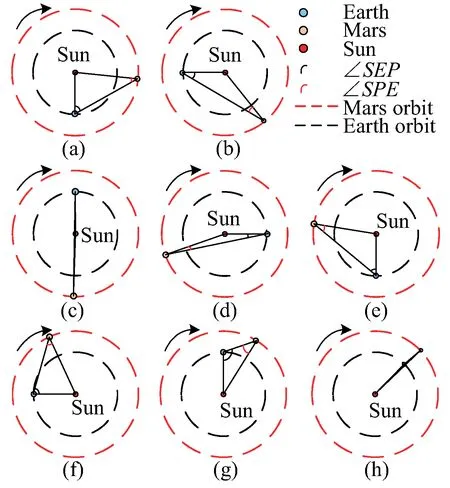
圖1 ∠SEP與軌道關系Fig.1 Diagram of ∠SEP and orbit

根據開普勒第三定律、在軌初始近點角、平均角速度和運行時間來計算真近點角：

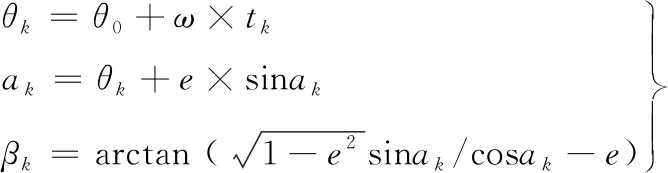
(1)

式中：θk為平近點角；θ0為初始平近點角；ω為平均角速度；tk為距離k時刻的時間；ak為偏近點角；初始化ak=θk；βk為真近點角；帶有下標k的各項變量表示tk時刻對應的值；e為偏心率，地球、火星的公轉偏心率分別為ee=0.016 675，em=0.093 334。

一個地火公共周期內地球-太陽-火星夾角∠ESP與地球、火星的軌道真近點角關系的具體表達式如下：

式中：βe為地球的真近點角；βm為火星的真近點角。βe，βm均可由式(1)計算得到。求得∠ESP后，再根據三角形ESP三邊和內角之間的幾何關系，得出∠SEP和太陽-探測器-地面站夾角∠SPE的大小：

∠SPE=180°-∠SEP-∠ESP

式中：Rsm為太陽到火星的距離；Rem為地球到火星的距離。對上述模型進行Matlab仿真，初始化∠SEP為85°，仿真結果如圖2所示。

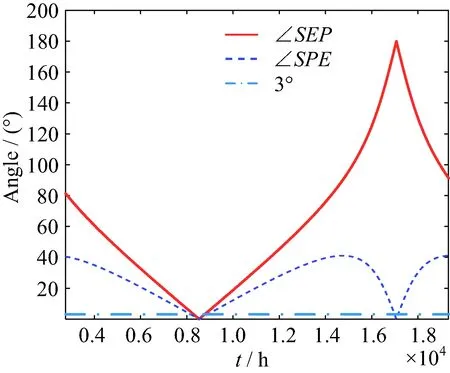
圖2 ∠SEP初始值為85 °時隨時間變化規律Fig.2 The variation of ∠SEP with time when initial value is 85 °

由圖1和圖2可知，C點對應的太陽、地球、衛星的位置關系是三者處在同一條直線上，并且衛星和地面站分別位于太陽的兩側，∠SEP和∠SPE均接近于0°。此時通信鏈路穿過太陽的湍流介質，閃爍效應會對鏈路產生強烈的影響[12]；同時地面站和衛星的天線均指向太陽，強大的太陽輻射會使接收天線的熱噪聲溫度急劇升高。H點對應日地星三者位置關系為太陽、地面站和衛星在同一條直線上，地面站和衛星位于太陽的一側，∠SEP接近于180°，∠SPE接近于0°。此時不考慮太陽閃爍對通信鏈路的影響；但衛星的天線在指向地面站的同時，也直接指向了太陽，太陽輻射對衛星天線熱噪聲溫度的影響不可忽視。下一節中具體分析在上合階段太陽輻射對鏈路的影響。

3 地面站天線接收噪聲溫度理論分析

3.1 歸一化噪聲溫度分析

太陽引起的天線噪聲溫度主要依賴于天線的波束寬度和波束中心軸指向太陽視距圓盤的相對位置[9]。接收天線的半波功率寬度HPBW和太陽的視距圓盤角直徑Dθ的大小關系把黑體與波束的關系分成了兩種情況，即HPBW≤Dθ和HPBW≥Dθ，如圖3所示。

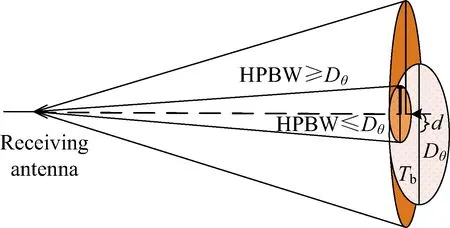
圖3 相對太陽視距圓盤寬度與兩種天線波束寬度幾何關系Fig.3 The geometry of an antenna beam with two beam widths relative to the Sun

圖3中HPBW=70λ/D，其中λ為電磁波的波長，D為天線口徑；Dθ為太陽的視距圓盤角直徑。

假設太陽是一個角直徑為0.53°的恒溫圓盤。地面站接收到的歸一化太陽噪聲溫度表示為[10]：

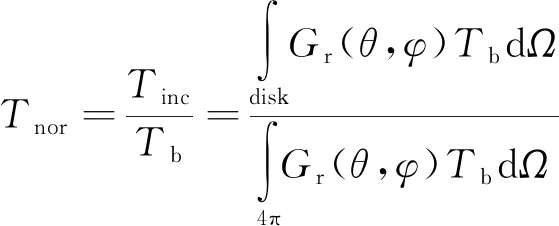
(2)

式中：Tnor為歸一化噪聲溫度；Tinc為噪聲溫度的增加量；Tb為太陽的表面亮溫度；Gr(θ,φ)為接收天線視線軸指向黑體時的功率瓣；θ為偏離天線波束視軸的角度；dΩ為立體角,滿足

θ∈(0,π)，φ∈(0，2π)。

需要注意的是，式(2)中的分子是對太陽視距圓盤立體角的積分，而分母是對整個空間立體角(4π)的積分。天線歸一化功率瓣(包括主瓣和旁瓣)可以用貝塞爾函數來近似：

式中：J1為一階貝塞爾函數。歸一化的太陽噪聲溫度在不同地面站天線波束半功率寬度/熱體的視距圓盤角HPBW/Dθ的不同表現的仿真結果如圖4所示，其中d為太陽中心到波束中心的距離，Rs為太陽半徑。

為了直觀地反映地面站受到太陽輻射影響時長，把(Tsmax,0.05Tsmax)范圍內的滾降系數α定義為：

α=Tsmax(1-0.05)/Δ∠SEP

(3)

利用式(3)計算圖4中的歸一化太陽噪聲溫度滾降系數α。α越大，太陽的影響時長越短；α越小，太陽的影響時長越長。不同HPBW/Dθ對應的α統計如表1所示。

由表1和圖4可以清晰地看出，歸一化噪聲溫度最大值隨HPBW/Dθ減小而不斷增大；但是不同曲線的滾降的系數α隨HPBW/Dθ的減小而增大，換言之，太陽對地面站接收噪溫的影響時長隨HPBW/Dθ的減小而縮短。

3.2 環火段地面站接收噪溫與∠SEP具體關系分析

在歸一化太陽噪聲溫度的分析總結的基礎上，對太陽噪聲的公式進行變形推廣，得到探火過程中地面站接收到的太陽噪聲溫度的大小與∠SEP，天線口徑和頻率之間的具體函數關系，其推廣過程如下：

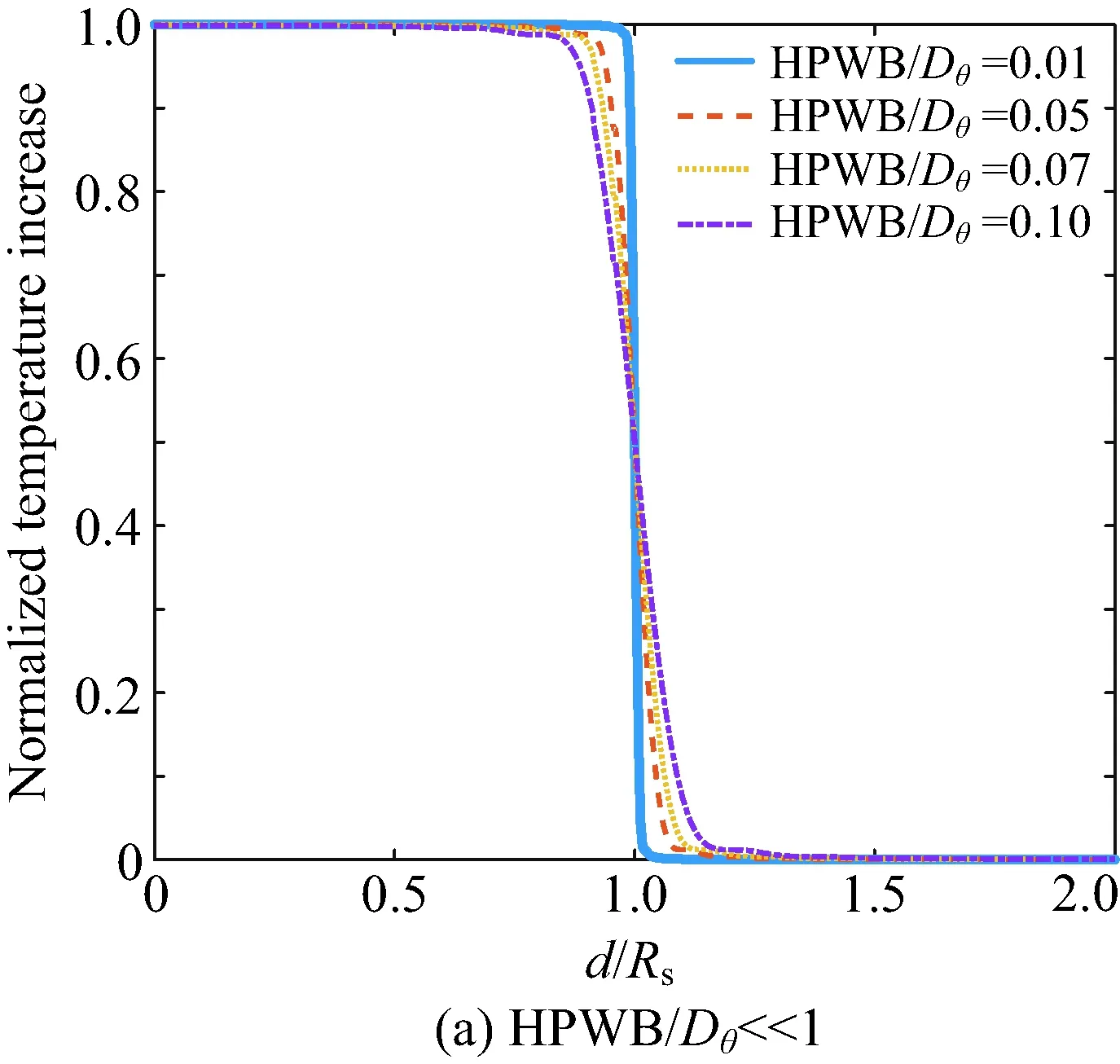
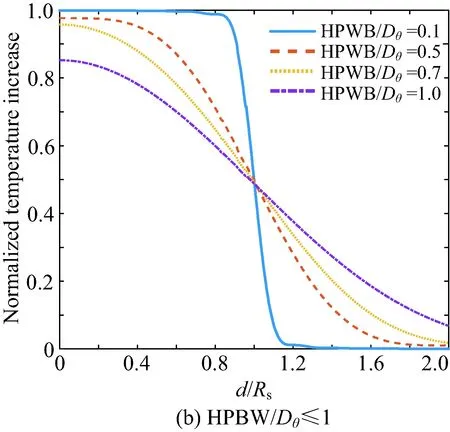
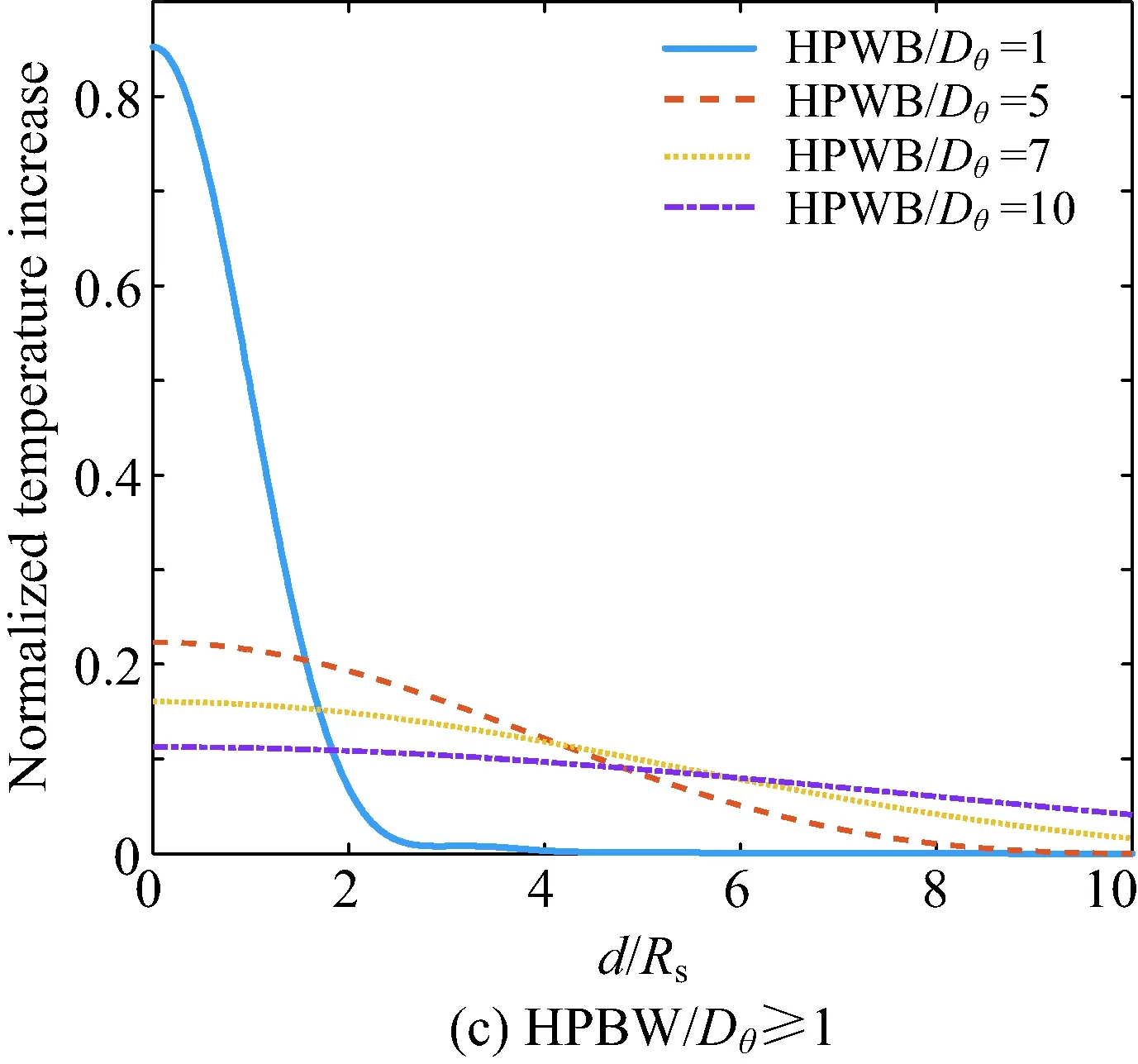
圖4 歸一化太陽噪聲溫度與d/Rs關系Fig.4 The relationship between normalized solar noise temperature and d/Rs

上式可簡化為：

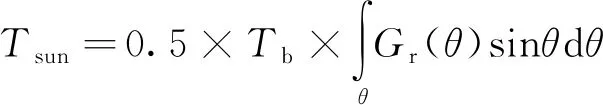
(4)

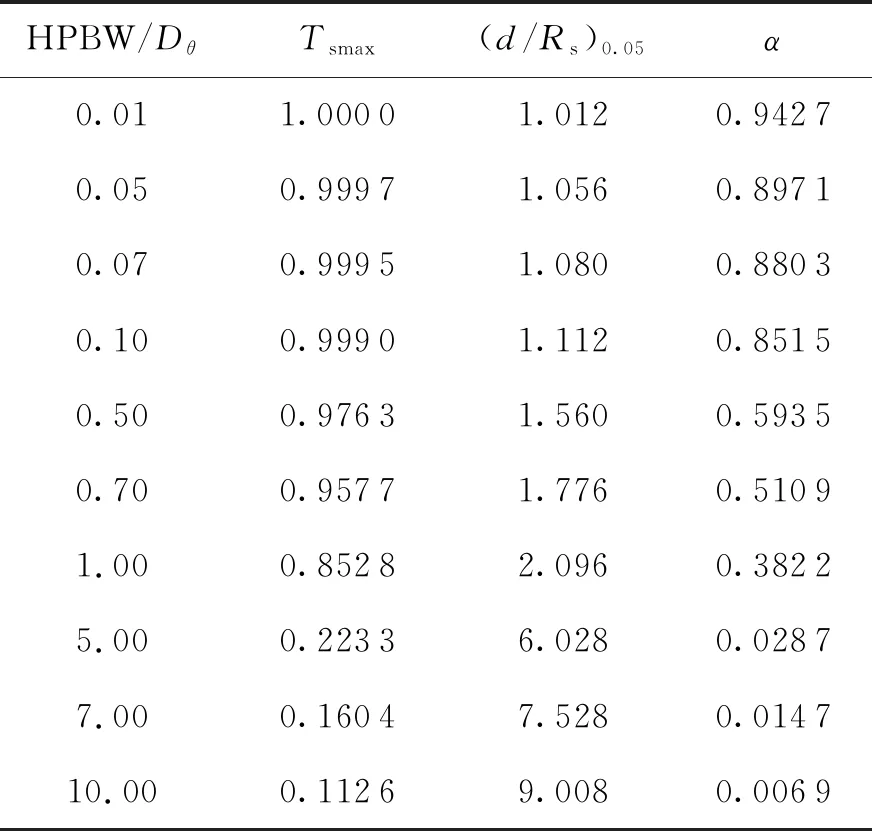
表1 滾降系數參考

Tb與太陽活動、太陽風通量有密切關系[13-15]；本文為了簡化計算，只考慮平靜時期太陽輻射對鏈路和地面站接收天線的影響。根據NASA深空通信手冊中提供的平靜時期的太陽亮溫度與頻率關系式[7]，在選定通信頻率后，式(4)中的Tb可通過下式計算得到：

Tb=5 672λ0.245 17=5 672×(c/f)0.245 17

式中：c為光速；f為頻率。

最關鍵的一步是確定積分范圍。根據∠SEP和太陽圓盤視角關系來確定積分范圍：

1)∠SEP≤Dθ/2

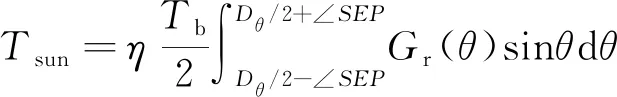
(5)

2)∠SEP>Dθ/2

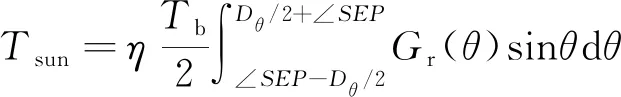
(6)

式中：η為天線效率，取值范圍為0<η<1。利用式(5)(6)對Ka、X、S波段不同口徑的地面站天線接收到的太陽噪聲溫度進行仿真，仿真結果如圖5所示。

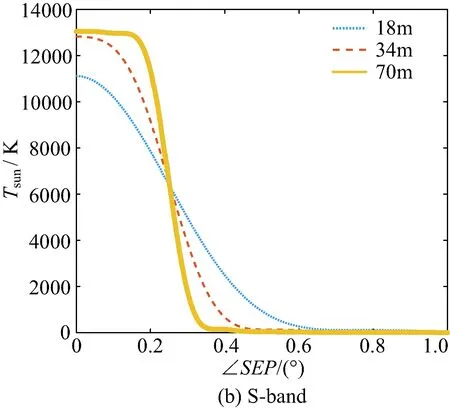
圖5 天線接收太陽噪聲溫度隨∠SEP變化Fig.5 The solar noise temperature received by antennas changes with ∠SEP

由圖5(a)可知，當地面站天線口徑固定為34m時，使用S波段進行傳輸，其最大接收噪聲溫度高達12 830K，其大于50K的∠SEP范圍在(0,0.667°)，α為0.593 5；使用X波段最大接收噪聲溫度達到9 538K，其大于50K的∠SEP范圍在(0,0.36°)，α為0.851 5；Ka波段的最大接收噪聲溫度達到6 880K，其大于50K的∠SEP范圍在(0,0.277°)，α為0.914 2；因此在天線口徑一定時，傳輸頻率越高，地面站接收噪溫峰值Tsmax越小，同時太陽輻射對地面站的影響時間也越短。

圖5(b)表明，當通信頻率固定為S波段時，口徑為70m，34m，18m的天線的接收噪聲溫度峰值Tsmax依次為13 040K，12 830K，11 120K；可見頻段一定時，Tsmax隨天線口徑的增加而升高。影響時長的分析中，接收噪聲溫度大于50K的角度范圍分別為：(0.0.46°)，(0,0.66°)，(0,0.955°)；因此天線口徑越大，太陽輻射對鏈路的影響時間越短。

參考文獻[16]中的鏈路計算過程，利用以下設置參數，分析了在太陽輻射影響下，信噪比Eb/N0與口徑、頻率和∠SEP的變化規律。其中EIRP為等效全向發射功率。

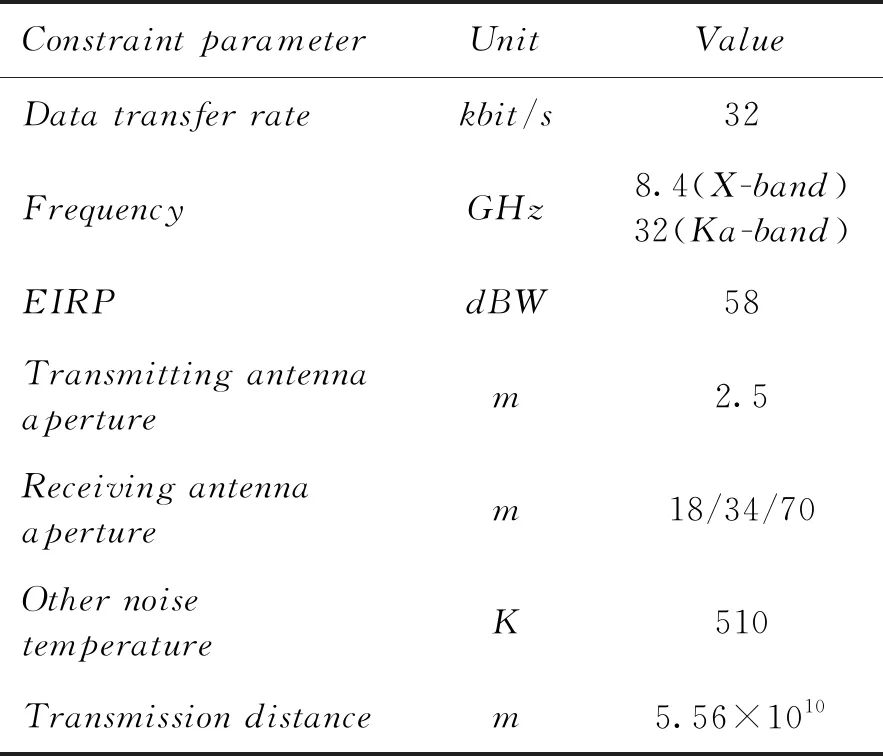
表2 仿真環境參數設置

由圖6可直觀看出，天線口徑固定為70m時，使用Ka頻段(32GHz)比X頻段(8.4GHz)的最低信噪比Eb/N0高約1.35dB；在頻率固定為Ka頻段時，70m口徑的天線受太陽影響的最低信噪比相對于18m口徑天線的最低信噪比提高了11.79dB，且影響弧長縮短了約0.3°。由此可知最優化的鏈路設計是使用Ka頻段和口徑為70m的接收天線，其最低信噪比為5.28dB，且太陽輻射的影響弧長可以控制在0.5°以內。雖然使用大口徑天線和高頻率信號會帶來波束窄，對準困難的問題；但是對于深空通信的遠距離目標來說，其影響相對不大。

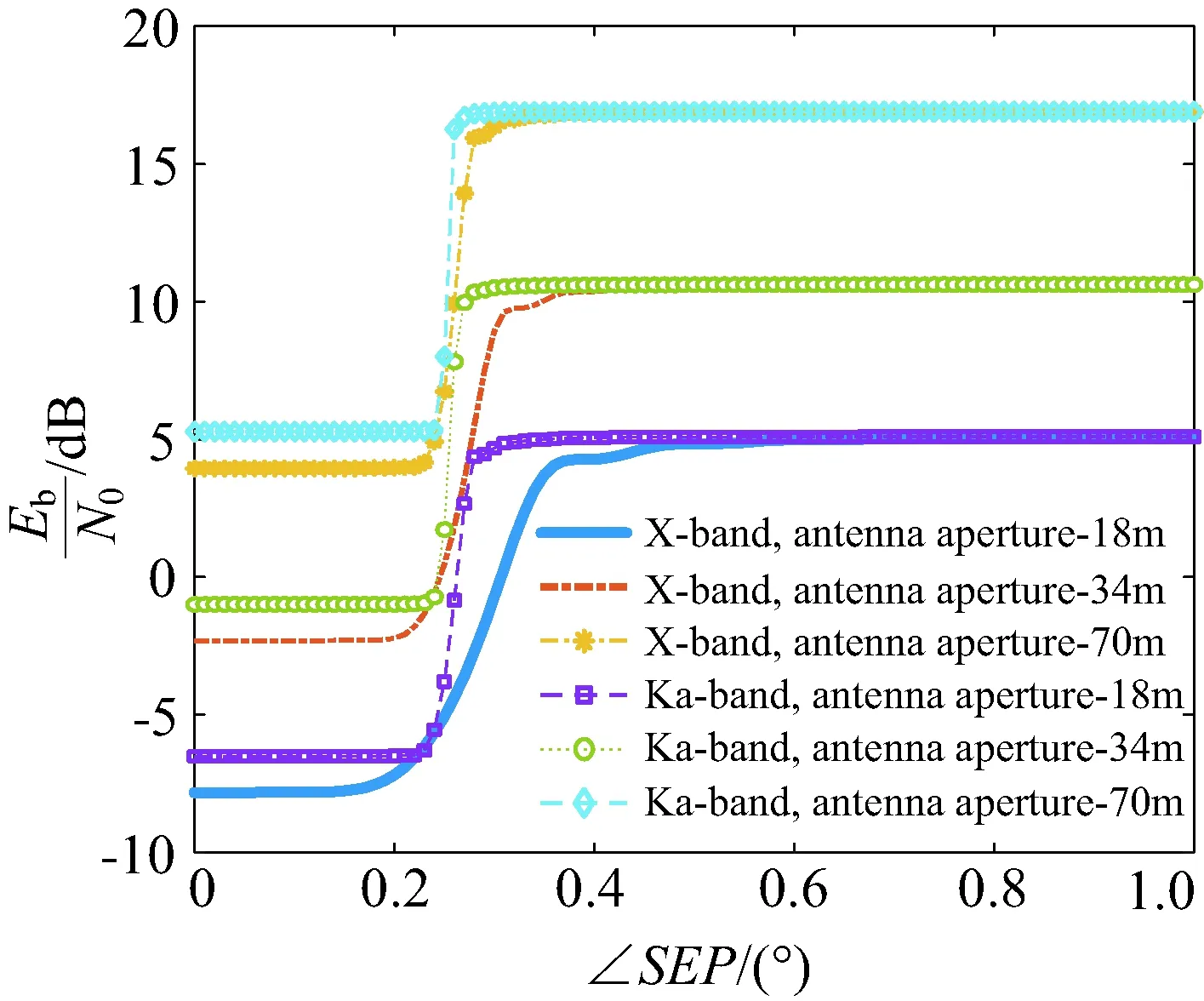
圖6 Eb/N0與∠SEP關系Fig.6 The relationship between Eb/N0 and ∠SEP

4 太陽影響下鏈路參數設計建議

結合文獻[17-20]對太陽閃爍的影響研究可知，太陽閃爍對于鏈路的影響程度也與∠SEP、頻率等參數密切相關。閃爍指數、頻譜擴展、相位擴展、時延擴展等均隨∠SEP的減小而增大，并隨頻率的升高而得到改善。根據NASA建議[5]，在X波段下，當∠SEP>3°時，即可不用考慮太陽閃爍對于鏈路的影響。根據前文對X頻段以上的太陽輻射的影響分析可知，當∠SEP>0.5°時，可不考慮太陽輻射對鏈路的影響；由此可見，雖然在∠SEP<0.5°時太陽輻射對鏈路的影響不可忽視，但在深空探測上合階段，太陽閃爍仍是影響鏈路通信質量最為關鍵的因素。

基于以上研究，為火星探測上合階段鏈路參數設計提出建議如下：根據前文分析及考慮深空通信的常用頻段，建議使用X(8.2～8.6GHz)，Ka(31.8～32.3GHz)或更高頻段進行通信。根據上述歸一化和非歸一化的綜合分析，建議把HPBW/Dθ控制在小于0.1范圍內，因此若使用X頻段進行通信，建議地面站使用口徑50m以上的天線進行通信；如使用Ka頻段進行通信，建議地面站使用口徑13m以上的天線進行通信。這樣可以盡可能降低太陽對地面站影響，可實現地面站受到太陽輻射的干擾可控。

∠SEP在(0,0.5°)范圍內，太陽輻射和太陽閃爍均會對鏈路造成嚴重的影響，這個時段可以選擇中斷通信。∠SEP在(0.5°,3°)范圍內，此時主要克服太陽閃爍對通信鏈路的影響[21]。根據太陽閃爍指數m和Rician分布中的Rician因子之間的關系，可以將深空信道電波傳播的模型用Rician信道來表示[17]。BPSK/QPSK，相干FSK和非相干FSK的誤碼率隨閃爍指數和調制方式變化的曲線如圖7所示，其中FSK調試方式使用分集接收。

根據圖7的仿真結果和表1的仿真環境參數設置，可以推算出不同閃爍指數m下，使用不同調制方式實現安全通信(BER≤10-6)的信息速率Rb，如表3所示。

在m=0.3時，BPSK/QPSK的傳輸性能優于FSK，BPSK/QPSK的最高通信速率為81.750 4kbit/s，比相干FSK高了16.97kbit/s，相比于非相干FSK提高了34.93kbit/s。當閃爍指數m升高到0.5時，FSK的傳輸性能優于MPSK，使用非相干FSK相比于BPSK/QPSK傳輸速率提高了14.79kbit/s，使用相干FSK其傳輸速率較非相干FSK提高了10.38kbit/s。當閃爍指數升高到0.8時，FSK的優勢更加明顯。所以在閃爍強度m<0.3時，建議使用BPSK/QPSK調制方式；當m>0.3時，建議使用分集接收的FSK調制方式，因為FSK調制技術更容易實現頻率分集，因此更有利于克服Rician信道的多重散射效應，來保證通信質量。

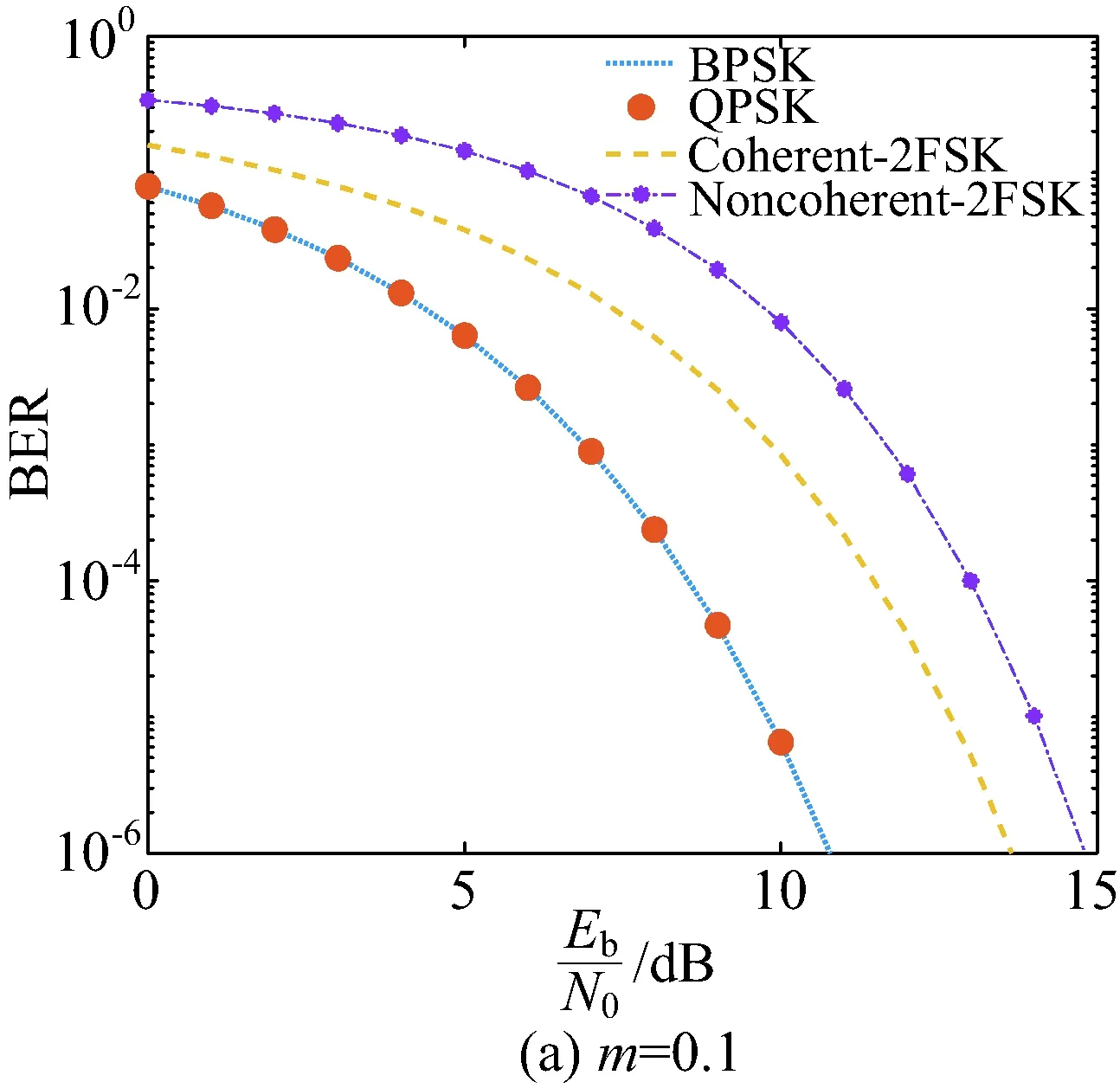
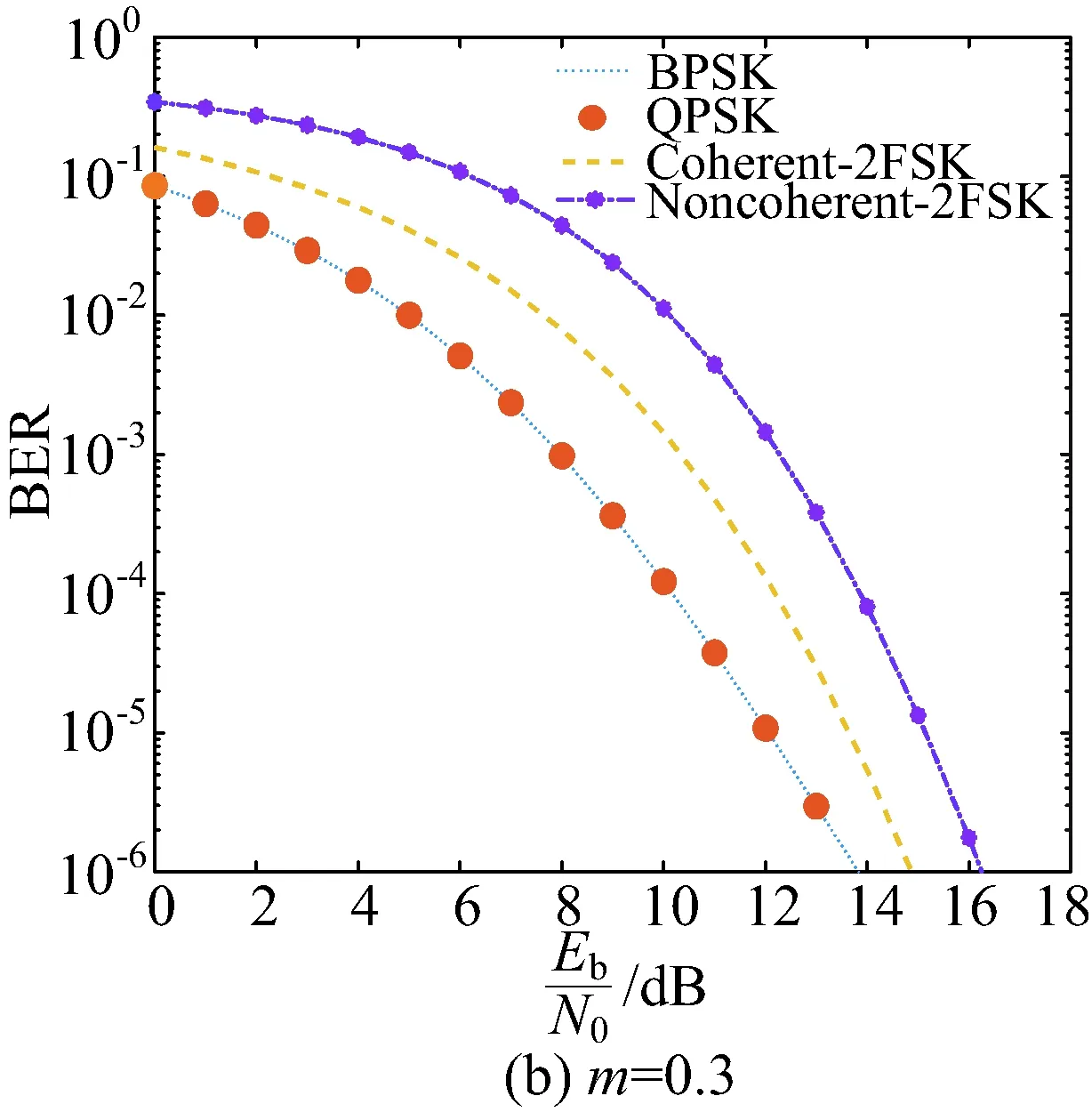
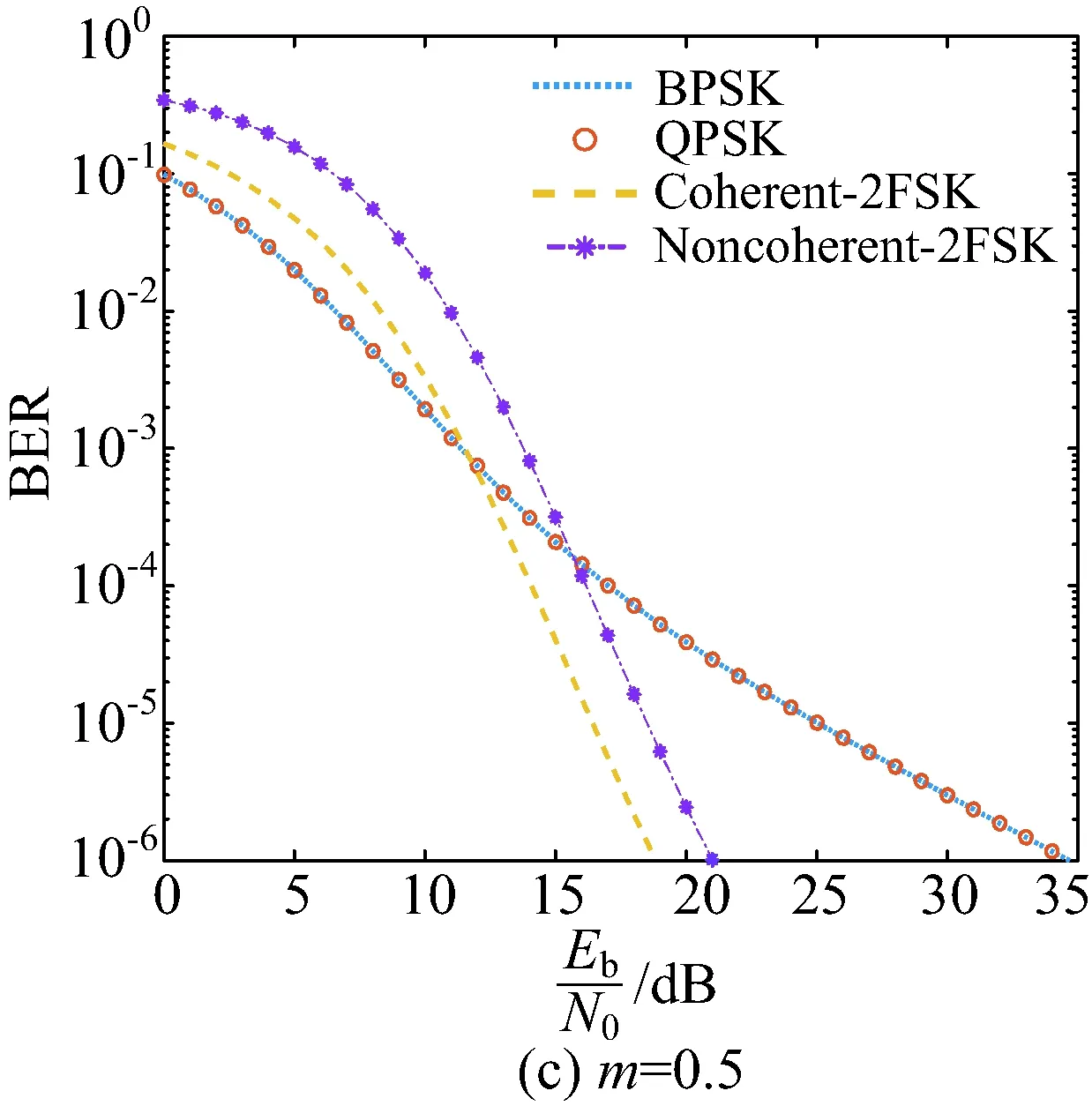
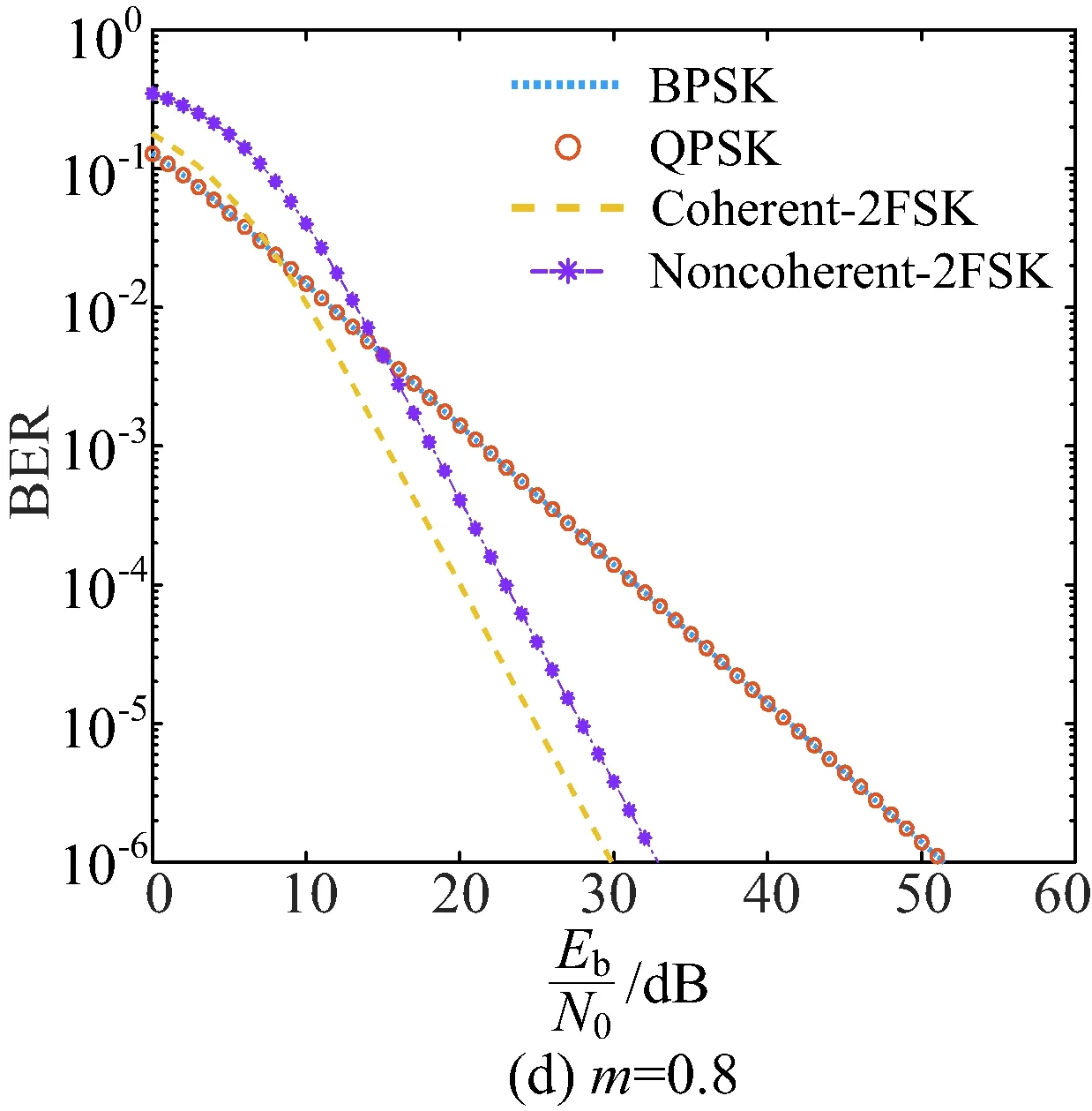
圖7 誤碼率隨閃爍指數和調制方式變化曲線Fig.7 BER curve with scintillation index and modulation mode

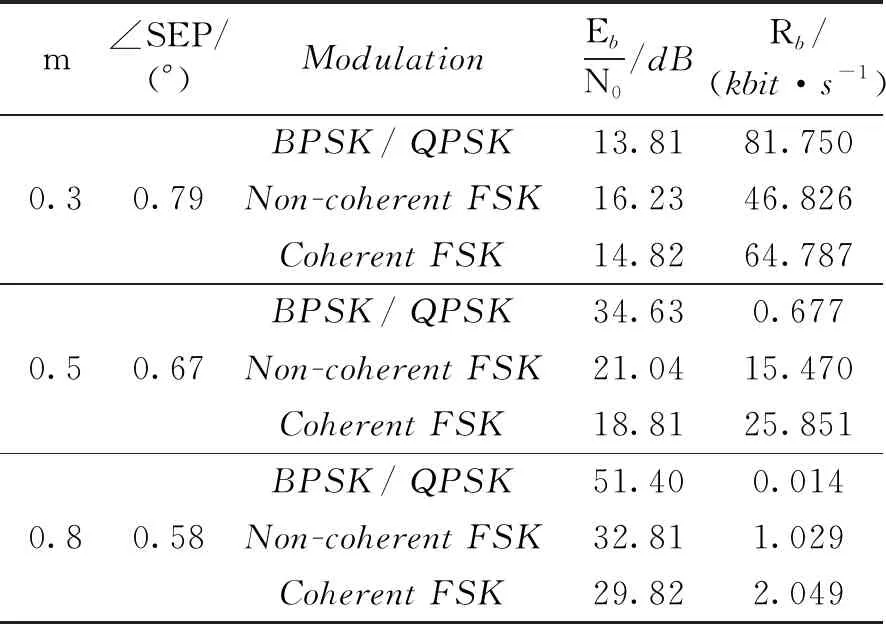
表3 BER≤10-6時不同調制方式的信息速率和信噪比統計

5 結論

本文完成對環火段日地星軌道的數學建模，分析了∠SEP隨時間變化的規律和發生日凌現象的原因。在對火星探測軌道關系研究分析的基礎上，詳細分析了上合階段，地面站接收到的太陽噪聲溫度大小和∠SEP，天線口徑，頻率之間的定量關系。得出以下結論：

1)深空通信的上合階段，太陽輻射會對接收天線造成嚴重的噪聲干擾。若使用Ka波段進行通信，使用口徑70m天線進行接收，其接收噪溫峰值高達6 880K；若使用X波段，34m口徑天線進行接收，其接收噪溫峰值達9 538K，強烈的噪聲溫度足以使通信鏈路中斷。

2)太陽對地面站接收噪聲溫度影響與通信頻率、天線口徑的關系如下：

——當頻率一定時，地面站天線口徑越大，所接收到的太陽噪溫最大值Tsmax越大；但對應的接收噪溫與∠SEP曲線的滾降系數α越大, 如當HPBW/Dθ=0.01時，α=0.942 7；當HPBW/Dθ=10時，α降至0.006 9；即口徑越大，地面站收太陽輻射的影響時間越小。

——當口徑一定時，頻率越高，Tsmax越小，這與太陽亮溫和頻率的關系有關；頻率越高，α越大，地面站收太陽噪聲溫度影響時間越短。

3)結合本文對環火段上合階段太陽對鏈路的影響分析，給出了不同∠SEP范圍內，通信鏈路頻率，調制方式和天線口徑等參數的設置，為火星探測工程中鏈路參數設置提供了參考價值。