非合作失效航天器繩系拖曳系統(tǒng)研究

孫瑞琦，祁瑞

北京理工大學 宇航學院， 北京 100081

1 引言

自1957年10月4日第一顆人造衛(wèi)星發(fā)射升空，人類航天活動日趨頻繁，在持續(xù)推進航天科技發(fā)展的同時，也不可避免地產(chǎn)生了大量太空垃圾，即空間碎片。空間碎片不僅長期占據(jù)寶貴的軌道資源，其極高的飛行速度也給在軌人員和資產(chǎn)造成威脅，一旦發(fā)生碰撞將產(chǎn)生大量小碎片，有可能進一步引起碰撞鏈式反應[1-2]。而僅依靠大氣阻力等方式清除碎片的速度遠比不上不斷增加的發(fā)射任務等導致的空間碎片的產(chǎn)生速度[3-4]，因此，必須對空間碎片進行主動清除。在眾多碎片主動清除技術(shù)中，繩系拖曳系統(tǒng)[5]因其具有結(jié)構(gòu)簡單、質(zhì)量輕、成本低、系統(tǒng)結(jié)構(gòu)參數(shù)可變、捕獲距離大等特點，受到國內(nèi)外學者的廣泛關(guān)注[6]。作為空間碎片的一類，失效航天器因體積和質(zhì)量較大，在確定清除目標時應得到足夠重視。并不是所有的失效航天器都是因為燃料耗盡而失效，有些航天器可能因器件損壞、通訊模塊故障而失效，雖然航天器已不受地面控制，但星上姿態(tài)穩(wěn)定的自動控制模塊依然有效，將失效星穩(wěn)定在某一固定指向。對這類目標開展繩系拖曳清除，會發(fā)生拖船與目標在姿態(tài)穩(wěn)定指向上的抗衡效果，從而表現(xiàn)出復雜的動力學與控制特性。

目前已有許多學者展開了關(guān)于繩系復合體的研究[7-8]，針對其離軌階段的動力學與控制問題，許多學者初步將拖船和目標簡化為質(zhì)點，觀察系統(tǒng)整體運動規(guī)律并對控制問題進行研究。Wen等將拖船和失效航天器均簡化為質(zhì)點，基于勢能整形與阻尼注入設(shè)計了一種張力控制律，在拖曳離軌過程中，只需要系繩長度反饋即可有效地使TST系統(tǒng)達到穩(wěn)定狀態(tài)[9]；劉海濤等忽略拖船與目標的姿態(tài)運動，針對TST系統(tǒng)離軌過程中系繩擺動抑制，設(shè)計了系繩張力控制律，并構(gòu)造了使擺動衰減的期望繩長收放速率[10]；王班等針對切向推力作用下繩系復合體拖曳離軌過程中的縱向振動問題提出一種以速度控制為外環(huán)、以張力控制為內(nèi)環(huán)的雙閉環(huán)振動控制法[11]。以上簡化模型均忽略了拖船與失效航天器的姿態(tài)運動與姿態(tài)控制能力，這有可能導致系繩纏繞等問題從而引起系統(tǒng)失穩(wěn)，因此為更加精細地描述系統(tǒng)運動，許多國內(nèi)外學者在簡化模型的基礎(chǔ)上進一步將目標視作剛體，對拖曳過程中的動力學與控制問題進行研究。Aslanov等將拖船視為質(zhì)點，失效航天器視為剛體，分析了目標慣量、系繩長度等對繩系拖曳系統(tǒng)動力學模型的影響，得出當系繩始終處在張緊狀態(tài)時，可實現(xiàn)對失效航天器的成功拖曳等結(jié)論，針對此系統(tǒng)，進一步分析發(fā)現(xiàn)失效航天器的振蕩幅度主要取決于系繩[12]。在失效航天器質(zhì)心與系繩固定點連線和系繩之間的角度較大時，系繩的振蕩幅度也會增大，易使系繩松弛進而導致系繩纏結(jié)[13]；在此基礎(chǔ)上，還研究了失效航天器帶有剩余燃料[14]與柔性附件[15]時對系統(tǒng)穩(wěn)定的影響，推導了TST系統(tǒng)在中心重力場中的運動方程，但并未考慮拖船與失效航天器的自主控制能力；為更加準確地描述真實繩系拖曳系統(tǒng)模型，Jaworski等將拖船與失效航天器視作剛體，將系繩看作彈簧—質(zhì)點模型，在拖船有姿態(tài)控制能力的情況下，研究了系繩材質(zhì)對于目標姿態(tài)運動的影響，通過仿真得出較大的系繩彈性系數(shù)會增加失效航天器碰撞的風險的結(jié)論[16]；針對繩網(wǎng)清理失效航天器的繩系復合體拖曳離軌過程，Benvenuto等將繩系復合體中的拖船與失效航天器均視為剛體，研究了離軌過程中系繩松弛與推力器關(guān)機時導致的危險情形，將離軌策略分為單次點火和多次點火兩種情況，分別給出了避免拖船與失效航天器碰撞的解決方案[17]。更加精細的動力學模型帶來了復雜的控制問題，為實現(xiàn)對系統(tǒng)的姿軌控制，Linskens設(shè)計了滑模控制器對拖船的相對軌道與姿態(tài)進行控制，并將其性能與線性控制器進行對比，但并未給出失效航天器姿態(tài)的詳細信息[18]；Zhang等基于Takagi-Sugeno模糊模型，通過求解一組線性矩陣不等式，獲得系統(tǒng)的控制律，在目標有旋的情況下，通過拖船位置和系繩張力控制可以使系統(tǒng)在垂直于系繩的兩個方向上穩(wěn)定[19]；Jasper等提出了一種使用帶有燃料的火箭上面級與LEO區(qū)域失效航天器交會并通過系繩牽引離軌的方法，利用推力輸入整形法來減小推力器關(guān)機后拖船與失效航天器之間的相對運動來避免碰撞[20-21]；為增強系統(tǒng)的控制能力與魯棒性，Yang等建立了單繩拖曳系統(tǒng)的三維模型，在失效航天器初始旋轉(zhuǎn)的情況下通過系繩連接點偏置控制法與繩長控制使系統(tǒng)穩(wěn)定；并提出了失效航天器的多繩分叉拖曳系統(tǒng)，在失效航天器有不同初始角速度的情況下進行仿真，說明了所提出系統(tǒng)的有效性[22-23]。

以上研究均未考慮繩系復合體中失效航天器姿態(tài)可控的情況。在對具有姿態(tài)控制能力的失效航天器進行繩系拖曳時，會發(fā)生拖船與目標在姿態(tài)穩(wěn)定指向上的抗衡，拖曳方向易受影響，可能出現(xiàn)拖曳路徑漂移，從而導致清除任務的失敗。本文針對這一問題開展研究，將拖船與失效航天器均視為剛體，采用牛頓法對繩系拖曳系統(tǒng)進行了動力學建模，并針對失效的自旋穩(wěn)定航天器和三軸穩(wěn)定航天器分別開展了拖曳動力學與控制分析，研究了繩系復合體在拖曳離軌過程中的運動狀態(tài)，為帶有殘余姿態(tài)控制能力的失效航天器的清除與未來的空間攻防提供了參考。

2 系統(tǒng)描述

2.1 模型基本假設(shè)

如圖1所示，TST系統(tǒng)由拖船、失效航天器(下文中簡稱“碎片”)和連接兩航天器的一根柔性系繩組成，首先，做出如下假設(shè)：

1)除地心引力外，忽略其他外部擾動；

2)系繩受剪和受扭量級遠小于受拉的量級，因此忽略系繩所受的剪切力和扭矩，只考慮系繩所受拉力；

3)假設(shè)連接拖船與碎片的系繩無質(zhì)量，但具有剛度和阻尼；

4)拖船與碎片均被視為剛體。

圖1 TST系統(tǒng)模型示意圖Fig.1 Sketch of tethered space-tug system

2.2 坐標系定義

為描述系統(tǒng)各體之間的相對運動，定義如下坐標系：

1)地心赤道慣性系fe(CeXeYeZe)

慣性參考系，以地球質(zhì)心為中心，Xe沿著春分點方向；Ze垂直于地球赤道平面；Ye位于赤道平面，滿足右手定則。

2)軌道坐標系f0(C0X0Y0Z0)

原點C0固連在拖船質(zhì)心，Z0軸從原點指向地球中心；X0軸在軌道平面內(nèi)，垂直于軸并指向系統(tǒng)運動方向；Y0軸方向滿足右手定則。

3)拖船本體系f1(C1X1Y1Z1)

原點C1固連在拖船剛體質(zhì)心，三個坐標軸方向分別沿拖船的慣性主軸方向。

4)碎片本體系f2(C2X2Y2Z2)

原點C2固連在碎片剛體質(zhì)心，三個坐標軸方向分別沿目標的慣性主軸方向。

3 TST系統(tǒng)建模

3.1 坐標系轉(zhuǎn)換

本文中主要涉及的坐標系為：地心赤道慣性系fe、軌道坐標系f0、拖船本體系f1和碎片本體系f2。為了避免拖船與碎片姿態(tài)大角度變化時發(fā)生奇異，f1系與f2系相對于f0系的姿態(tài)分別通過四元數(shù)Q1=[q10,q11,q12,q13]T、Q2=[q20,q21,q22,q23]T來描述。

軌道系的三軸向量可表示為：

jo=-(Rs)e×(Vs)e/‖Rs×Vs‖

ko=-(Rs)e/‖(Rs)e‖

io=jo×ko

式中：(Rs)e、(Vs)e分別為拖船在慣性系下的位置矢量與速度矢量。

地心慣性系到軌道系的坐標轉(zhuǎn)換矩陣可以表示為：

Aoe=[io,jo,ko]T

f0系到f1系與f2系的坐標轉(zhuǎn)換矩陣分別為：

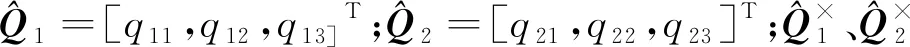
歐拉角按軌道坐標系“3-1-2”旋轉(zhuǎn)到本體坐標系，四元數(shù)與歐拉角的相應轉(zhuǎn)換關(guān)系為：

3.2 系統(tǒng)質(zhì)心動力學建模

TST系統(tǒng)在軌運行所受外力主要為重力與發(fā)動機的推力，拖船與碎片所受的重力可寫作：

式中：μ為地球引力常數(shù)；ms、md分別為拖船與碎片的質(zhì)量；Rs、Rd分別為拖船與碎片質(zhì)心的位置矢量。

由牛頓第二定律，拖船的質(zhì)心運動動力學方程可以表示為：

(1)

式中：fT為施加在拖船上的推力；Gs為拖船所受重力；Ts為拖船所受系繩拉力。

(2)

式中：Gd為碎片所受重力；Td為碎片所受系繩拉力。

3.3 碎片的質(zhì)心相對動力學建模

TST系統(tǒng)在高軌運行時，其位置向量的變化遠小于位置向量的大小，在慣性系下直接進行計算可能會引起較大誤差，因此考慮建立碎片相對于拖船的動力學方程。

碎片相對于拖船的位置矢量為：

rsd=Rd-Rs

將rsd對時間求導，有：

(3)

式中：ω0為軌道系相對慣性系的角速度矢量，滿足：

(4)

將式(3)兩邊同時對時間求導，有：

(d2rsd/dt2)o=d2(rsd)o/dt2+

(5)

將式(2)與式(1)相減，有：

(6)

由坐標系之間的轉(zhuǎn)換關(guān)系，可得：

(d2Rsd/dt2)o=Aoe(d2Rsd/dt2)e

(7)

聯(lián)立式(5)、(6)、(7)可得：

3.4 系繩張力模型

系繩拉力可以使用Kelvin-Voigt模型計算，將其近似為線彈性部分Te和阻尼的Tv線性組合：

T=Te+Tv

系繩的長度變化率可以通過系繩兩端點相對速度在系繩方向的投影來計算，即：

式中：VA為系繩在拖船上連接點處的速度矢量；VB為系繩在碎片上連接點處的速度矢量。

系繩兩端點的速度在慣性系下可分別寫作：

式中：ω1、ω2分別為拖船和碎片本體系相對于慣性系的角速度，由角速度關(guān)系可知：ωi=ωoi-ω0，(i=1,2)，其中，ωoi為拖船/碎片相對軌道系的角速度矢量；Ae1、Ae2分別為拖船本體系與碎片本體系到慣性系的坐標轉(zhuǎn)換矩陣。

3.5 拖船與碎片姿態(tài)動力學

采用四元數(shù)描述的拖船與碎片的姿態(tài)運動學方程如下：

將拖船與碎片視作勻質(zhì)長方體剛體，二者所受的重力梯度力矩在各自本體系f1與f2下的分量列陣為：

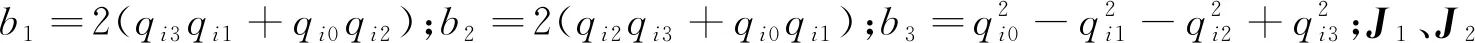
拖船與碎片的姿態(tài)動力學方程可分別寫作：

式中：M1、M2分別為拖船與碎片所受的外力矩；Mi=MiG+Mic+MiT,i=1,2，其中，MiG、Mic、MiT分別為拖船與碎片所受的重力梯度力矩、控制力矩與系繩拉力產(chǎn)生的力矩。

3.6 拖船姿態(tài)控制模型

為了維持拖曳方向穩(wěn)定，拖船具有姿態(tài)控制能力，當拖船實際姿態(tài)偏離期望姿態(tài)時，姿態(tài)控制系統(tǒng)對拖船施加控制力矩，把姿態(tài)穩(wěn)定在期望值附近。

在拖船控制律的設(shè)計中，采用姿態(tài)誤差四元數(shù)與誤差角速度來描述姿態(tài)運動：

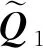
拖船的三個慣性主軸上各安裝有一個反作用輪，采用PD控制律，則拖船控制器輸出的控制力矩為：

式中：K1p、K1d為反饋增益；M1c為在拖船本體系下表示的控制力矩。

3.7 系統(tǒng)軌道描述與計算

本文采用改進的春分點軌道根數(shù)來描述系統(tǒng)的軌道運動，改進的春分點軌道根數(shù)與經(jīng)典軌道根數(shù)可通過下式進行轉(zhuǎn)換：

相應的高斯攝動方程如下：

(8)

式中：w=1+fcosL+gsinL；s2=1+h2+k2。 將軌道攝動方程(8)與系統(tǒng)運動微分方程同時積分，可以得出系統(tǒng)在慣性系下的軌道高度及角速度：

4 自旋穩(wěn)定碎片拖曳分析

4.1 自旋穩(wěn)定碎片姿態(tài)控制模型

當自旋穩(wěn)定碎片為對稱剛體時，章動角?為：

碎片自旋角速度ω2y較大且基本保持不變，因此可以通過減小橫向角速度ω2xz的大小來減小章動角?。

假設(shè)自旋穩(wěn)定碎片采用主動噴氣控制策略，推力器安裝在平行于碎片本體軸Y2方向的星體表面上，如圖2所示。

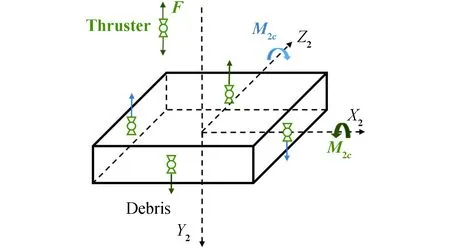
圖2 作用在自旋穩(wěn)定碎片上的推力示意Fig.2 Sketch of thrust on the spin stabilized debris

考慮角速度測量誤差，當控制力矩方向為碎片橫向角速度的反方向時，消章效果最好。具體的噴氣相位選擇方法為：

式中：ωon=J2yω2ytan?e/J2x為噴管開啟閾值；?e為章動角控制精度。

4.2 算例仿真

初始系統(tǒng)在橢圓軌道運行，拖船與碎片均有姿態(tài)控制能力，拖船為三軸穩(wěn)定，碎片為自旋穩(wěn)定。建立仿真模型，采用變步長龍格—庫塔方程對建立的動力學方程進行積分。系統(tǒng)輸入?yún)?shù)如表1所示。

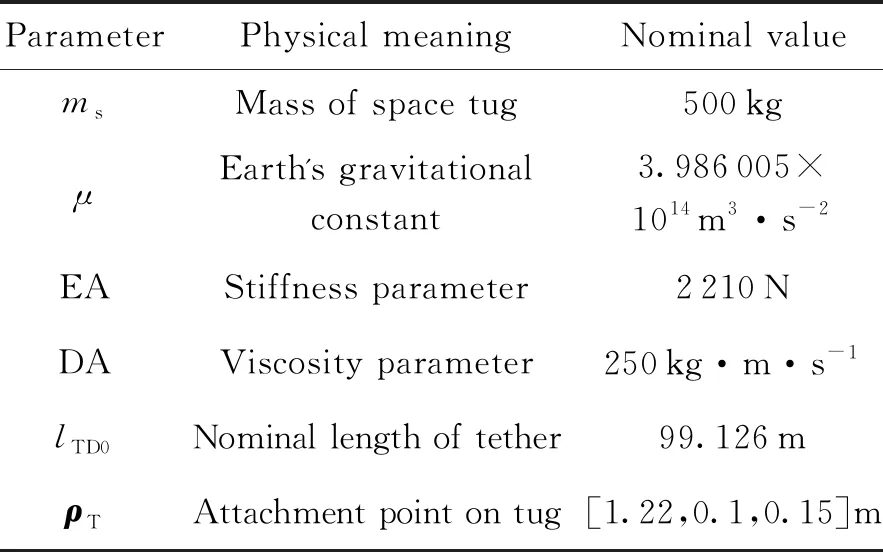
表1 TST系統(tǒng)參數(shù)

初始拖船繞各軸無轉(zhuǎn)動，主慣性矩[Jx1,Jy1,Jz1]為[1 500,1 500,500]kg·m2。碎片質(zhì)量md為400 kg, 主慣性矩[Jx2,Jy2,Jz2]為[700,1 200,700]kg·m2。初始以[0,-30(°)/s,0]旋轉(zhuǎn)，章動角控制精度?e取0.01°，期望自旋軸為垂直于軌道面的方向，初始拖船與碎片的本體系與軌道系重合，姿態(tài)四元數(shù)可表示為[q10,q11,q12,q13,q20,q21,q22,q23]T=[1,0,0,0,1,0,0,0]T，拖船的期望姿態(tài)四元數(shù)與歐拉角分別為Q1d=[1,0,0,0]T與Ω1=[0°,0°,0°]T；碎片理想姿態(tài)為自旋軸Y2與軌道系Y0重合，系繩在碎片上的連接點為[-2.12,0,0]，拖船上控制器的參數(shù)分別為K1p=[120,120,40]T與K1d=[1 200,1 200,400]T。

假定推力ft大小恒定，為比較不同推力大小對系統(tǒng)的影響，分別取幅值為5 N、10 N、15 N與20 N的推力進行仿真，推力方向均在本體系f1下沿-X1軸方向，隨拖船姿態(tài)改變而變化，如圖3所示。

圖3 作用在拖船上的推力示意Fig.3 Sketch of thrust on the space tug

軌道偏心率、軌道高度與軌道角速度如圖4所示。

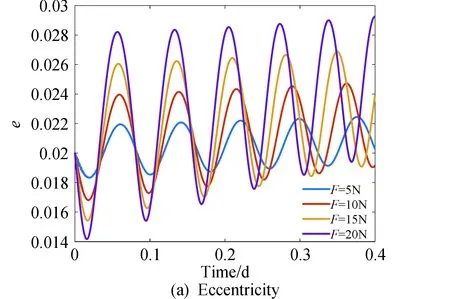
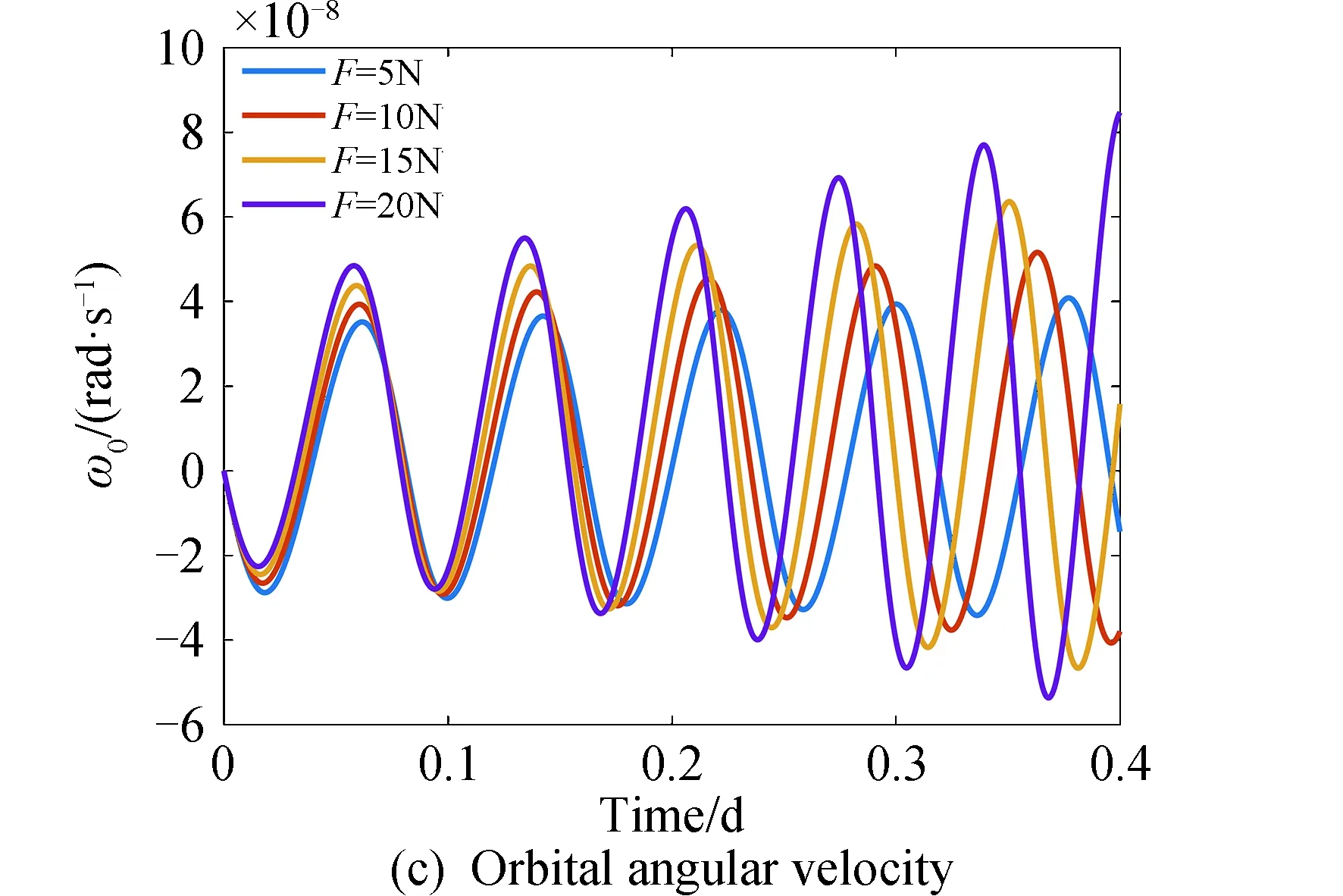
圖4 不同推力大小作用下軌道元素的時間歷程Fig.4 Evolution of system’s orbit under different thrust

由圖4可知，在給定的不同大小推力作用下，每一次振蕩都對應著系統(tǒng)繞地球一次完整的旋轉(zhuǎn)。如圖4(a)所示，偏心率隨時間振蕩增大，推力越大，偏心率振幅越大，振蕩越劇烈；由圖4(b)可知，由于施加在拖船上的推力與系統(tǒng)運動反向，系統(tǒng)的軌道高度沿螺旋線軌跡緩慢降低；相應地，如圖4(c)所示，軌道角速度隨著時間振蕩增大，振幅也隨時間緩慢增大。推力越大，軌道高度下降越快，軌道角速度越大，降軌效率越高。

如圖5所示，在0.4天的仿真時間內(nèi)，拖船與碎片的姿態(tài)角隨時間振蕩變化，均呈現(xiàn)出振幅衰減趨勢。當系統(tǒng)達到穩(wěn)定狀態(tài)時，拖船并未穩(wěn)定在理想姿態(tài)，碎片無法維持自旋；推力越大，姿態(tài)角收斂越快，且穩(wěn)定后振蕩較小，TST系統(tǒng)越快達到穩(wěn)定狀態(tài)。

圖5 不同大小推力作用下拖船與碎片姿態(tài)角時間歷程Fig.5 Time history of Euler angles of space tug and debris under different thrust

如圖6所示，由于推力方向會隨拖船姿態(tài)變化而變化，在不同大小推力作用下，TST系統(tǒng)的面外角與面內(nèi)角在給定時間內(nèi)穩(wěn)定到不同值，推力越大，面外角最終的穩(wěn)定值越大，面內(nèi)角在0°附近以不同振幅隨時間振蕩變化。

圖6 不同大小推力作用下TST系統(tǒng)面內(nèi)角、面外角時間歷程Fig.6 Time history of in-plane angle and out-plane angle of TST system

綜合圖4、圖5與圖6可知，推力主要影響系統(tǒng)的軌道，推力越大，系統(tǒng)降軌效率越高；同時推力大小對系統(tǒng)的姿態(tài)穩(wěn)定也起到一定的作用。

發(fā)動機推力幅值取10 N，分別改變系繩在碎片上的連接點位置進行仿真，系繩初始連接點的位置如表2所示，連接點1、2與3在碎片星體表面，4在自旋軸上，如圖7所示，紅色圓點表示系繩在碎片上的連接點；自旋穩(wěn)定碎片的三軸角速度、拖船碎片的姿態(tài)角與系繩張力分別如圖8～12所示。

表2 系繩在碎片上的連接點位置

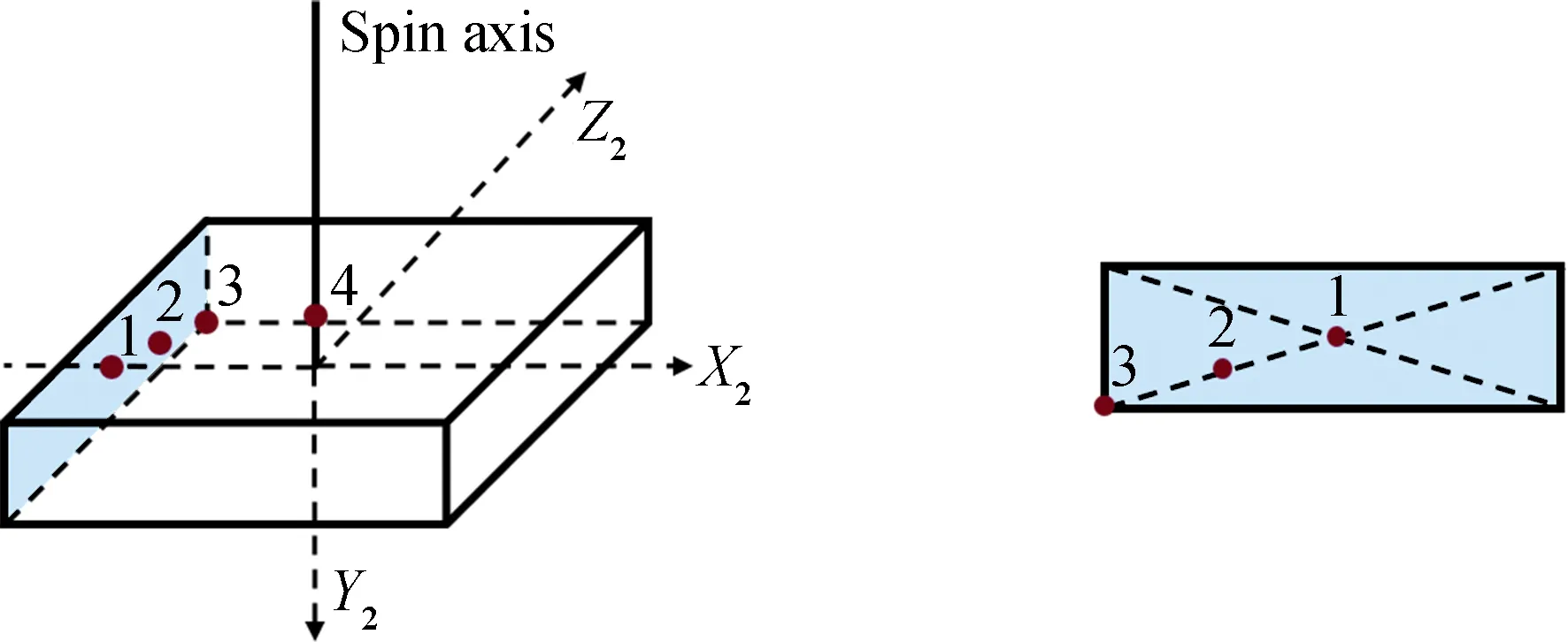
圖7 系繩在碎片上的連接點示意Fig.7 Sketch of attachment points on space debris

圖8 自旋穩(wěn)定碎片本體系下三軸角速度的時間歷程Fig.8 Time history of three-axis angular rate of spin stabilized debris

如圖8所示，在給定的仿真時間內(nèi)，碎片在本體系下沿三個軸的姿態(tài)角速度隨時間振蕩變化，最終穩(wěn)定在特定值附近以不同的振幅振蕩。當系繩連接點在位置1、2和3時，碎片的自旋角速度最終均穩(wěn)定在0(°)/s附近振蕩變化，無法維持自旋狀態(tài)，連接點越靠近表面邊緣，角速度振蕩越劇烈。當連接點在碎片的自旋軸上時，由于系繩張力在垂直于碎片自旋軸的方向，不改變目標自旋角速度的大小,只改變其方向，故碎片沿自旋軸方向的角速度大小一直保持在-30(°)/s，沿本體系X2、Z2方向的角速度最終在0(°)/s附近小幅度振蕩變化。

如圖9與圖10所示，在給定的仿真時間內(nèi)，拖船與碎片的三個姿態(tài)角隨時間振蕩變化，除碎片的俯仰角θ2之外，均呈現(xiàn)出收斂趨勢；拖船與碎片的姿態(tài)角在初始階段，系繩從松弛突然張緊，系繩張力在拖船與碎片上產(chǎn)生力矩，姿態(tài)角偏離理想狀態(tài)；在控制器與系繩的共同作用下，拖船的三個姿態(tài)角并未收斂到期望姿態(tài)，最終穩(wěn)定到不同特定值附近振蕩；當系繩連接點在碎片自旋軸上時，碎片的滾轉(zhuǎn)角φ2與偏航角ψ2最終在[-10°,10°]與[-78°,-88°]內(nèi)振蕩。如圖10所示，θ2在[-180°,180°]內(nèi)不斷振蕩，這是由于將四元數(shù)轉(zhuǎn)換為歐拉角時，反正切函數(shù)的值域有限制，由碎片的三軸角速度可知，碎片應為單向旋轉(zhuǎn)，θ2實際不斷增大，并非振蕩變化，TST系統(tǒng)的最終狀態(tài)如圖11所示，碎片自旋軸由垂直于軌道面變?yōu)樵谲壍烂娓浇袷帲槠@自旋軸以-30(°)/s的角速度旋轉(zhuǎn)。

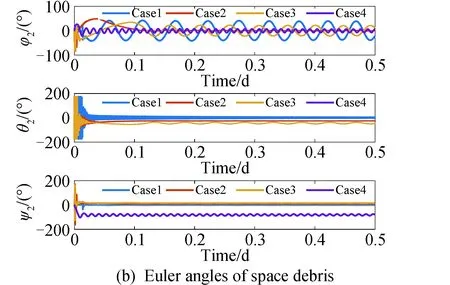
圖9 拖船與碎片姿態(tài)角時間歷程Fig.9 Time history of Euler angles of space tug and spin stabilized debris

圖10 當系繩連接點在碎片自旋軸上時碎片θ2的時間歷程Fig.10 Time history of θ2 when attachment point is on spinning axis

圖11 當系繩連接點在碎片自旋軸上時TST系統(tǒng)穩(wěn)定后的狀態(tài)示意Fig.11 TST system in equilibrium state when attachment point is on spinning axis

圖12 系繩張力大小的時間歷程Fig.12 Time history of tether tension

如圖12所示，隨著拖船與碎片之間距離增大，系繩張緊；而后，張力大小隨時間振蕩減小。在系繩阻尼作用下，系統(tǒng)逐漸趨于穩(wěn)定，系繩在拖曳過程中始終處于張緊狀態(tài)，張力最終穩(wěn)定在4.45 N附近振蕩變化。

5 三軸穩(wěn)定碎片拖曳分析

5.1 三軸穩(wěn)定碎片姿態(tài)控制模型

在碎片控制律的設(shè)計中，采用姿態(tài)誤差四元數(shù)與誤差角速度來描述姿態(tài)運動。

碎片的三個慣性主軸上各安裝有一個反作用輪，采用PD控制律，則碎片控制器輸出的控制力矩為：

式中：K2p、K2d為反饋增益；M2c為在碎片本體系下表示的控制力矩。

5.2 算例仿真

初始系統(tǒng)在橢圓軌道運行，同理采用變步長龍格—庫塔方程對系統(tǒng)動力學方程進行積分。系統(tǒng)輸入?yún)?shù)與表1相同，拖船主慣性矩[Jx1,Jy1,Jz1]為[1 500,1 500,500]kg·m2。碎片質(zhì)量md為700 kg, 主慣性矩[Jx2,Jy2,Jz2]為[2 000,2 000,700]kg·m2。

初始拖船與碎片繞各軸無轉(zhuǎn)動，拖船與碎片初始姿態(tài)四元數(shù)分別為[q10,q11,q12,q13]T=[1,0,0,0]T與[q20,q21,q22,q23]T=[cos (π/8),0,0,sin (π/8)]T，相對軌道系的期望姿態(tài)四元數(shù)分別為Q1d=[1,0,0,0]T、Q2d=[cos (π/8),0,0,sin (π/8)]T，拖船與碎片期望歐拉角分別為Ω1=[0°,0°,0°]T與Ω2=[0°,0°,45°]T。碎片初始姿態(tài)示意圖如圖13所示。

拖船上控制器的參數(shù)分別為K1p=[120,120,40]T與K1d=[1 200,1 200,400]T；碎片上控制器的參數(shù)分別為K2p=[160,160,56]T與K2d=[1 600,1 600,560]T。假定推力Ft為10 N，大小恒定，在本體系f1下沿-X1軸方向，會隨拖船姿態(tài)改變而變化。改變系繩在碎片星體表面連接點的位置進行仿真，系繩初始連接點的位置如表3所示，連接點如圖13所示，紅色圓點表示系繩在碎片上的連接點；拖船碎片的姿態(tài)角、碎片控制器輸出的力矩與系繩張力如圖14-圖16所示。

表3 系繩在碎片上的連接點位置

圖14 拖船與碎片姿態(tài)角的時間歷程Fig.14 Time history of Euler angles of space tug and three-axis stabilized debris

如圖14所示，在0.5 d的仿真時間內(nèi)，拖船與碎片的姿態(tài)角均隨時間振蕩變化，最終均未穩(wěn)定至期望姿態(tài)Ω1=[0°,0°,0°]T與Ω2=[0°,0°,45°]T；由于系繩連接在星體表面的不同位置，張力作用對碎片產(chǎn)生的力矩不同，故三軸姿態(tài)角最終穩(wěn)定在不同特定值附近，值的大小與系繩連接點位置有關(guān)；當連接點在位置1、2與3時，碎片的三個姿態(tài)角最終分別穩(wěn)定到[0°,0.1°,35.5°]、[-4.1°,-4.5°,41°]與[-7.2°,-7°,-44°]附近。

如圖15所示，在給定的仿真時間內(nèi)，碎片的控制器輸出的三軸力矩呈現(xiàn)出隨時間振蕩收斂的趨勢。碎片在初始受到系繩張力時，姿態(tài)產(chǎn)生變化，此時控制器通過輸出控制力矩來將碎片姿態(tài)保持在理想位置，結(jié)合圖14可知，TST系統(tǒng)達到穩(wěn)定狀態(tài)時，碎片的姿態(tài)角并未收斂至期望位置，故控制器輸出力矩不為0，穩(wěn)定后的姿態(tài)偏離理想姿態(tài)越多，控制器輸出的控制力矩越大。

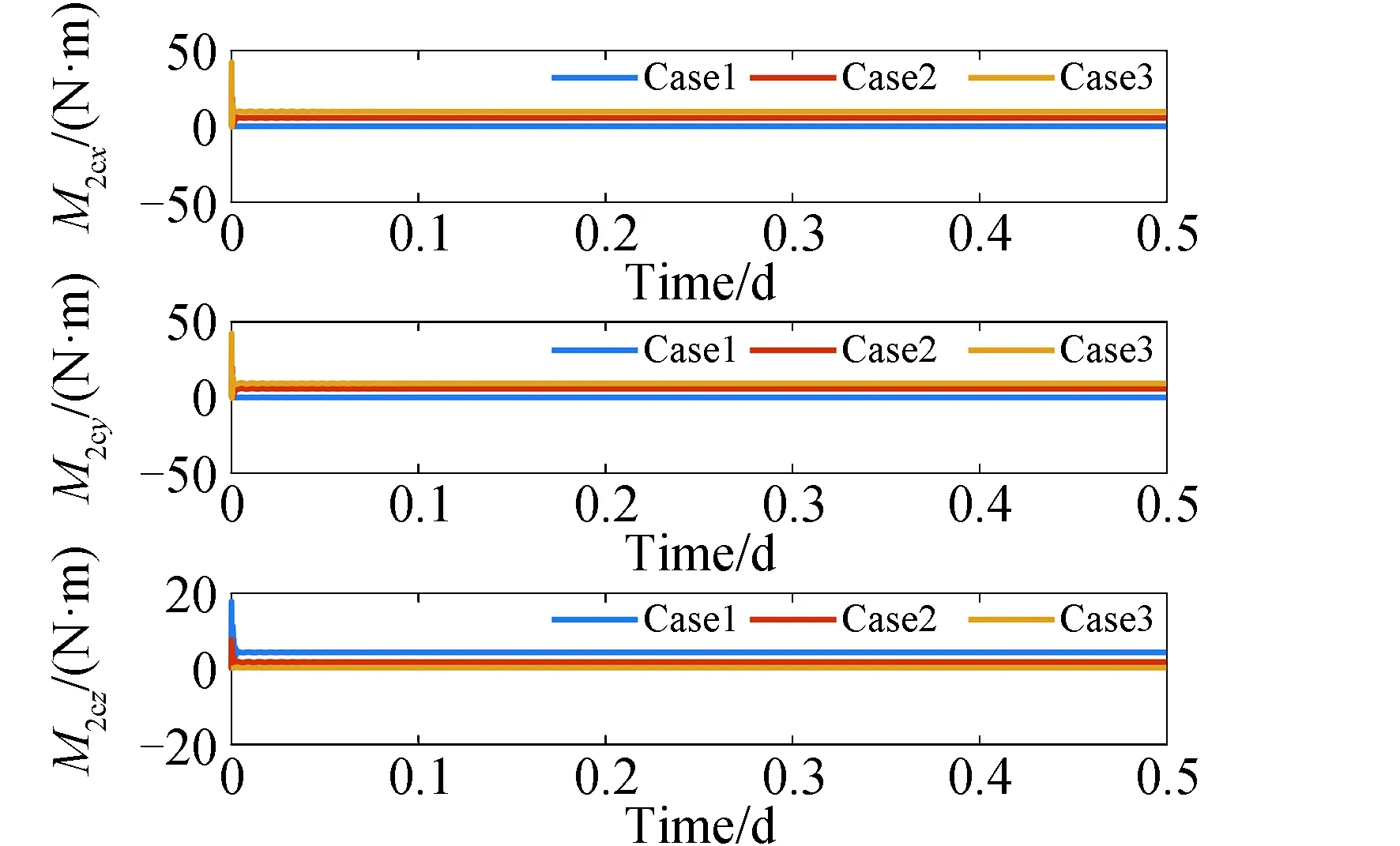
圖15 碎片控制器三軸輸出力矩Fig.15 Output torque of debris controller

如圖16所示，系繩在拖曳過程中始終處于張緊狀態(tài)，系繩連接點對系統(tǒng)達到穩(wěn)定狀態(tài)時系繩的張力并無明顯影響。

6 結(jié)論

本文針對帶有殘余姿態(tài)控制能力的空間碎片的繩系拖曳系統(tǒng)，采用牛頓法建立了系統(tǒng)的動力學模型，考慮目標穩(wěn)定方式分別為自旋穩(wěn)定與三軸穩(wěn)定兩種情況，分析了拖曳系統(tǒng)動力學與控制行為，并研究了不同系繩連接點的影響，通過仿真得到下列結(jié)論：

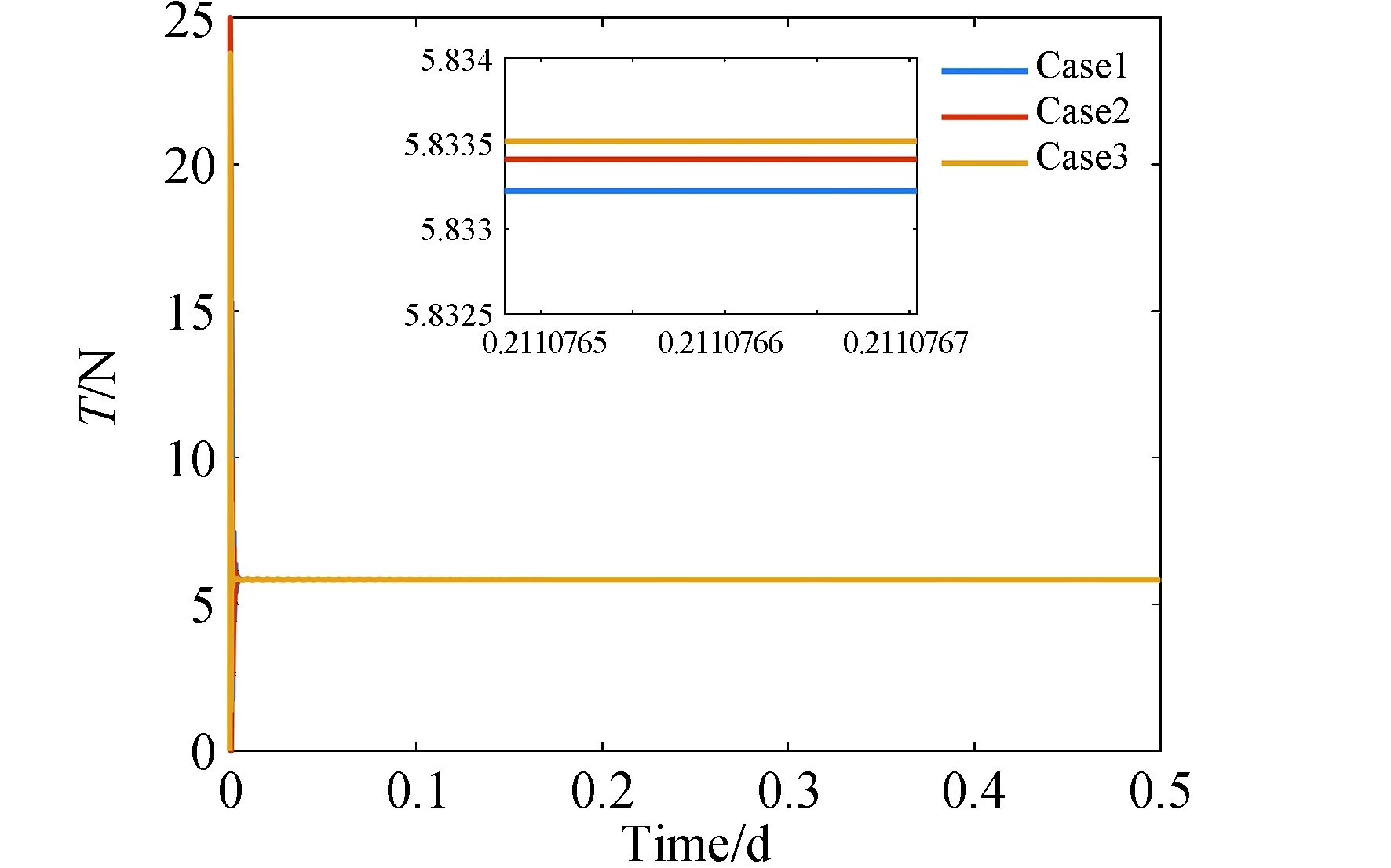
圖16 系繩張力大小的時間歷程Fig.16 Time history of tether tension

1)推力主要影響系統(tǒng)的軌道，同時對拖船與碎片的姿態(tài)穩(wěn)定也起到一定的作用；推力越大，系統(tǒng)降軌效率越高，拖船與目標的姿態(tài)角越快達到穩(wěn)定狀態(tài)。

2)當目標為失效自旋穩(wěn)定碎片時，若系繩連接點在星體表面，碎片無法保持自旋狀態(tài)，拖船與目標的三個姿態(tài)角均在控制律作用下逐漸穩(wěn)定到特定值附近；若系繩連接點在星體自旋軸上，則僅自旋軸方向發(fā)生改變，自旋角速度變化不大，此時系繩會出現(xiàn)扭曲。

3)當目標為失效三軸穩(wěn)定碎片時，拖曳組合體的姿態(tài)在目標姿態(tài)控制與拖船拖曳的雙方抗衡下逐步收斂，收斂后的組合體穩(wěn)定姿態(tài)與目標姿態(tài)控制能力和拖船推力幅值等系統(tǒng)參數(shù)有關(guān)。

4)本文研究了利用TST系統(tǒng)清除帶有姿態(tài)控制能力的失效航天器中的動力學與控制問題，為此類空間碎片的安全清除與未來空間攻防提供了參考。后續(xù)將進一步展開針對使用TST系統(tǒng)清除質(zhì)量參數(shù)、慣量參數(shù)與控制參數(shù)未知的失效航天器中的未知參數(shù)估計問題與系繩張力控制律的研究。