Quantifying coherence with dynamical discord?
Lian-Wu Yang(楊連武) and Yun-Jie Xia(夏云杰)
1School of Physical Science and Intelligent Engineering,Jining University,Qufu 273155,China
2Shandong Provincial Key Laboratory of Laser Polarization and Information Technology,Department of Physics,Qufu Normal University,Qufu 273165,China
Keywords: quantum coherence,dynamical discord,relative entropy
1. Introduction
Quantum coherence is an important feature of quantum mechanics. In recent years, quantum coherence was considered to be a physical resource in quantum information processing[1,2]and gained lots of attentions.[3,4]Quantum discord as a kind of quantum correlations, which can exists in unentangled systems, was regarded as an important quantum resource.[5–9]Quantum discord was used to implement some tasks, such as remote state preparation,[10]information encoding,[11]and quantum computation.[12]These two kinds of resources were considered to be the specific manifestation of the superposition principle in quantum mechanics.Previous studies have showed some connections between the quantum coherence and discord.[13–16]
Resources can be converted into each other. Local coherence can be converted into entanglement via incoherent operations,[17–19]and converting coherence into discord was studied in Ref.[20]. Other resource conversions among nonclassicality and quantum correlations were also studied in Refs. [21–26], and some related experiments were made in the optics and superconducting systems.[27–30]It is benefit for systematic study of the various notions of quantumness with resource theories,[31–35]due to it can quantify the quantumness in an objective manner, and this quantification satisfies the constraints of monotonicity under incoherent operations.
For better understanding the relations among the various notions of nonclassicality, it is meaningful to investigate the resource conversion from quantum coherence to correlations. Maet al.showed that quantum coherence can be converted into discord via bipartite incoherent operations, and the amount of coherence bounds the discord. Based on the measures of the relative entropy, these two quantities are identical.[20]The similar result is provided for the created entanglement in Ref. [19]. Recently, Theureret al.studied the relations between dynamical coherence and dynamical entanglement,and they provided a quantitative connection between the dynamical coherence and the dynamical entanglement.[36]According to the results of Refs.[19,20],the coherence of single quantum systems is equal to the dynamical entanglement and discord,respectively,and note that these two formulas are identical.We know that entanglement and discord are different notions, so there exist some conditions in the initial quantum state to distinguish it. We focus on the discord in this paper.
For quantifying the coherence with the dynamical discord,it is necessary to calculate the created discord and the coherence of quantum systems. Although the theory of quantum discord is well developed, calculating the discord of generic quantum systems is complicated. We adopt two specific quantum systems that the discord and coherence can be calculated,and these two specific quantum systems are created by incoherent operations.Is the created discord equal to the coherence displaying in the initial quantum systems? What the conditions should be satisfied in the initial states that the coherence is equal to the created discord? We resolve these questions in this work.
In this paper, we study the operational resource conversion between quantum coherence and discord via two specific quantum systems. In the conversion from coherence to discord, we restrict the operations to the bipartite and multipartite controlled-not gate operations. We find that the coherence of initial quantum systems bounds the bipartite dynamical discord and the inequalities are saturated under the particular conditions of the initial state.The similar result is provided for the multipartite quantum systems. We also show the advantage of characterizing coherence with dynamical discord than dynamical entanglement.
2. Preliminaries
We review the definitions of coherence and discord from resource theories. The relative entropy of resource has an operational interpretation in resource theories,which was firstly defined for entanglement theory in Ref. [31]. The relative entropy is a unique measure in reversible quantum resource theories,[37]and the unique asymptotic rate of interconversion among static resources under operations.[38]The relative entropy of resource is also the optimal rate in the resource erasure.[39,40]Due to the properties above,the relative entropy is an important measure in quantum resource theories. For the two quantum statesρandω,the relative entropy is defined asS(ρ||ω)≡?tr(ρlogω)?S(ρ), whereS(ρ)=?tr(ρlogρ)is the von Neumann entropy ofρ.[41]

where{|i〉}and{|j〉}are the reference basis of subsystemsAandBrespectively, withAas the control qubit andBas the target qubit.[19]
Recently, the notions of the dynamical coherence and dynamical entanglement were proposed in Ref. [36], that is,when a quantum state be generated from local states with the help of quantum operations, the coherence and entanglement of the generated state are called dynamical coherence and dynamical entanglement, respectively. In a similar manner, in this paper, the dynamical discord is the discord presenting in the states which be generated from local states with the help of quantum operations.
3. Characterizing coherence with dynamical discord in bipartite pure states
We now analyze the conditions of quantifying coherence with dynamical discord when a product pure state is converted to an correlated state via the CNOT gate operation.
Theorem 1 For the initial product stateρAB=(α|0〉+β|1〉)?(a|0〉+b|1〉) the evolved state under the CNOT gate isUCN(ρAB) =αa|00〉+αb|01〉+βa|11〉+βb|10〉, and if|a|2=0 or|a|2=1 the coherence of the coherent control states is equal to the dynamical discord of the evolved states,C(ρA)=D(UCN(ρAB)).
Proof: Performing the CNOT gate on the control qubit and the target qubitρAB=(α|0〉+β|1〉)?(a|0〉+b|1〉),the product state evolves into
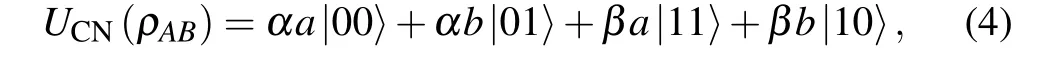
where|α|2+|β|2=1 and|a|2+|b|2=1. We have known that quantum discord reduces to the entanglement for pure states,for a bipartite pure state,the relative entropy of discord is equal to the entropy of the subsystem,D(ρAB) =S(ρA),whereρA=trB(ρAB).[5]We calculate the dynamical discord of the evolved state,

whereh(x1)=?x1logx1?(1?x1)log(1?x1) is the binary Shannon entropy,the parameters arex1=|α|2with 0≤x1≤1,andx2=|a|2with 0≤x2≤1. As well known thath(x1)is a symmetric concave function ofx1with 0≤x1≤1 the symmetric point is 1/2,h(1/2) = 1 is the maximal value,henceh(x1)≥0 andh(x1)∈[0,1]. Similarly, we obtainh(x2)∈[0,1]and the function of coherenceC(ρAB)∈[0,2].
The coherence can be converted into discord under the CNOT gate if the control qubit is the coherent states.[20]If the control state is given, i.e.,|α|2=c, wherecis a constant, thenh(x1) is also a constant. From the concavity of the functionsH(x) andh(x2) and the majorization theory,whenx2=|a|2=1/2, namely,x=1, we findD(UCN(ρAB))is the minimal value, and simultaneously,C(UCN(ρAB)) is the maximal value. Whenx2varies from 1/2 approaching to zero,orx2varies from 1/2 approaching to 1 namely,the variablexvaries from 1 tox=|β|2?|α|2, we get to know that the quantitiesD(UCN(ρAB)) becomes larger, and the quantitiesC(UCN(ρAB)) becomes smaller. Whenx2=|a|2=0 orx2=|a|2=1, namely,x=|β|2?|α|2we find the maximal value ofD(UCN(ρAB))is arrived,and simultaneously,the minimal value ofC(UCN(ρAB))is arrived,too.Furthermore,these two extreme values are equivalent,

Unifying the analysis above,we obtain the difference between the coherence and the dynamical discord

which holds when|a|2=0 or|a|2=1.
The target state is pure incoherent state with the conditions|a|2=0 or|a|2=1. Due to the additive properties of the coherence,[42]for the product statesρA ?ρBwe haveC(ρA ?ρB)=C(ρA)+C(ρB). So the coherence of the control state is equal to the dynamical discord of the evolved state under CNOT gate,

In other words,by using the CNOT gate as an incoherent operation on the product statesρAB, when the coherent control state isα|0〉+β|1〉and the incoherent target states is|0〉or|1〉,the coherence of the coherent control states is equal to the dynamical discord of the evolved states. The evolved state areα|00〉+β|11〉orα|01〉+β|10〉.The coherence of the coherent control state is

This completes the proof.
4. Characterizing coherence with dynamical discord in bipartite mixed states
We now analyze the conditions of quantifying coherence with dynamical discord when a product mixed state is converted to an correlated state via the CNOT gate operation.Perform the CNOT gate on the product stateρA ?ρB, and the evolved states is

The Bell-diagonal (BD) states are simple states which keep high relevance to the theoretical and experimental research in quantum information. The BD states also named T-states or two-qubit states with maximally mixed marginals,[43]which include the well-known Bell and Werner states[44]and often be employed as resources for performing tasks such as entanglement activation and distribution via discord-type correlations.[45–47]The BD state is defined as





the coherence of single-party systems is equal to the amount of the dynamical discord without generating dynamical entanglement via the CNOT gate operations. That is to say,characterizing the coherence with dynamical discord possesses more advantages than dynamical entanglement.

Through the above analysis,we conclude that the conditions of the initial quantum states for characterizing coherence with dynamical discord are different from different measures.
5. Characterizing coherence with dynamical discord in multipartite systems

which takes any pure incoherent qubit state|i〉?|j1〉···?|jN〉to another pure incoherent state,UMCN(|i〉?|j1〉···?|j1〉)=|i〉?|mod(i+j1,2)〉···?|mod(i+jN,2)〉. For multi-qubit systemsρA ?ρ?N?1B,what conditions should be satisfied if the coherence of the control state is equal to the dynamical discord of the evolved state under the MCNOT gate?
Extending the above results to the multi-qubit systems we can obtain the following results. For the initial product state with a pure coherent control state and anN ?1-partite pure incoherent target state (α|0〉+β|1〉)?|0〉?N?1, the evolved state under MCNOT gate is
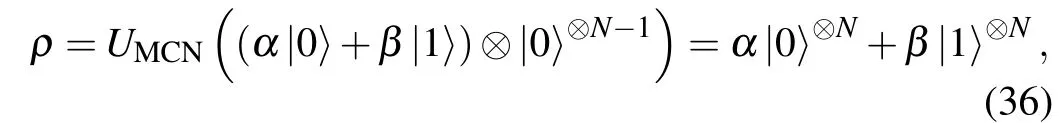
which is the so-called maximally correlated state.[51]While quantum discord reduce to entanglement for pure states,[5,9]we can calculate entanglement to represent the discord in multipartite quantum systems. For quantifying entanglement in multipartite quantum systems,the genuine multipartite entanglement measures are generalized from the bipartite entanglement measures,[51]



For multi-qubit systemsρA ?ρ?N?1B, if the initial quantum state with particular conditions as above,the coherence of the control state is equal to the dynamical discord of the evolved states under the MCNOT gate.
6. Conclusions

Via this process of resource conversion, we show the relations between the coherent states and the genuine correlated states by the coefficients of the initial quantum states.Through revealing the connections between the coherence of single quantum systems and the dynamical discord in particular composite systems,this work provides useful methods for realizing experiment of quantum resources conversion. It is important to realize a unification between the notions of coherence and discord from a quantum informational viewpoint,and we confirm this work makes a practical step in this direction.
- Chinese Physics B的其它文章
- Modeling the dynamics of firms’technological impact?
- Sensitivity to external optical feedback of circular-side hexagonal resonator microcavity laser?
- Controlling chaos and supressing chimeras in a fractional-order discrete phase-locked loop using impulse control?
- Proton loss of inner radiation belt during geomagnetic storm of 2018 based on CSES satellite observation?
- Embedding any desired number of coexisting attractors in memristive system?
- Thermal and mechanical properties and micro-mechanism of SiO2/epoxy nanodielectrics?