Merging and splitting dynamics between two bright solitons in dipolar Bose–Einstein condensates?
Xin Li(李欣) Peng Gao(高鵬) Zhan-Ying Yang(楊戰營) and Wen-Li Yang(楊文力)
1School of Physics,Northwest University,Xi’an 710069,China
2Shaanxi Key Laboratory for Theoretical Physics Frontiers,Xi’an 710069,China
3Peng Huanwu Center for Fundamental Theory,Xi’an 710127,China
4Institute of Modern Physics,Northwest University,Xi’an 710069,China
Keywords: bright soliton,Bose–Einstein condensate,dipolar soliton
Matter-wave solitons have become the focus of much recent research,[1–9]and their interactions manifest as abundant dynamical results. Elastic interaction dominates under the effect of atoms’contact interaction,including collision,interference,and tunneling dynamics.[10–15]Recently,the creation of dipolar Bose–Einstein condensates(BECs)brought new possibilities for research on localized structures(including solitons)and their interaction.[16–22]The dipolar effect has two main characteristics,i.e.,long-range and anisotropic features.[23–28]The former admits the stabilization of multi-dimensional solitons and new localized waves (like soliton molecules and the dark solitons with ripples),[29–35]while the latter contributes on the formation of anisotropic solitons.[36–40]Unlike the contact interaction, the dipolar interaction between atoms could induce the appearance of inelastic interactions between solitons.[29,34,35,41,42]It was observed that two in-phase bright solitons merged into a(stable or unstable)binding state or repel each other,[41,42]while two out-of-phase solitons formed a bound state with a stable oscillating frequency.[29,42]These observed interaction phenomena indicate different processes of energy transfer,prompting us to study their quantitative dynamical features and clarify their formation mechanism.In addition,it is also necessary to focus on how the dipolar strength and initial phase difference influence the soliton interaction.
In this paper,interaction between two bright solitons with zero initial velocities in one-dimensional dipolar BECs is studied. The two bright solitons can merge into a breathing wave,and then split or propagate constantly after several oscillating periods, under different dipolar strengths. The splitting is found to be asymmetric,and the influence of dipolar effect on the asymmetry is discussed. For the breathing wave without splitting, its oscillating period decreases with the dipolar strength increasing and is independent of the initial separation of solitons. In addition,the phase difference of initial solitons admits more various interaction results.
Considering the short-range contact and long-range dipolar interactions between atoms, the dynamics of condensates can be described by the nonlocal nonlinear Schr¨odinger equation. In the one-dimensional cases,its dimensionless form is

whereψis the macroscopic wavefunction of condensates,xandtare the spatial and temporal coordinates, respectively.V(x) denotes the external potential. The nonlocal response functionR(x)has the form

Depending on the atomic s-wave scattering lengthasand its background valueas0,gc=as/|as0| is the coefficient of short-range local interaction. The integral term including response functions denotes the long-range dipole–dipole interaction term,wheregd=ad/|as0|is its coefficient. The characteristic dipole lengthad=μ0d2m/12πˉh2, wheremanddare the mass and magnetic dipole moment of atoms oriented along thexaxis,respectively. Here,we consider the cases in which both the local and nonlocal interactions are attractive(gc=1 andgd>0).

wherex0and?are the separation distance and phase difference of the two solitons. Equation(2)describes the initial set of two solitons with the zero initial velocity.

Fig.1. Density evolution plots of initial condition(2)when(a)gd=0,(b)gd=0.5,and(c)gd=1.2. They illustrate the motionless,splitting,and merging dynamics of soliton interaction, respectively. (d) Initial amplitude profiles in the above three cases,where the red dashed,black solid,and blue dotted dashed curves correspond to gd=0,0.5,and 1.2.Other parameters are gc=1,x0=8,and ? =0.
Let us start with the cases of?=0, where the two solitons are in-phase. We set the atom number as constant. By the split-step Fourier method,the real-time evolutions of soliton interaction are studied.[43]There are three different situations of soliton interactions. Firstly, when the dipole–dipole interaction is absent (i.e.,gd=0), the density evolution plot is shown in Fig. 1(a), where the two solitons keep motionless. Secondly,when the dipolar strengthgdis increased into 0.5, the solitons attract each other and then separate with a large velocity [see Fig. 1(b)]. Thirdly, we setgdas a more large value 1.2. As depicted in Fig. 1(c), the solitons merge into a breathing wave with a stable frequency. The above results illustrate three different interaction dynamics of solitons,namely the parallel moving, splitting, and merging. They are obviously influenced by the dipolar strengthgd. Moreover,the dipolar strengthgdalso impacts on the time when the solitons encounter. From Figs.1(a)–1(c),the two solitons collide earlier and earlier withgdincreasing. We also illustrate the three kinds of initial amplitude profiles in Fig.1(d)(as the solitons on the left- and right-hand sides are symmetric aboutx=0,only the latter is depicted). There are slight differences between the shapes of three profiles. In a word, the interaction between two stationary solitons is significantly different under variationalg,when the initial separationx0between them is fixed. To explore the transition process between the three phenomena, we employ the initial condition (2) and enlarge the strength of dipole–dipole interaction from 0. We find that there is a criticalgdvalue(~0.75)between the splitting and merging dynamics and the critical value will be different with the atom number changing.Furthermore,when the local interaction are absent,we can also get the same results.
In order to study and describe the both two phenomena,we consider the total energy of the system,

whereEk,Eint, andEddare the kinetic, local interaction, and nonlocal interaction energies, respectively. Their specific expressions are

In our numerical simulations, we set the window width to beX0, so the range ofxis?X0/2

Fig.2. Energy evolution plots when(a)gd=0.5 and(b)gd=1.2.They correspond to Figs.1(b)and 1(c),respectively. The red dashed line denotes the total energy, while the black, blue, and green curves denote the kinetic,local,and nonlocal interaction energies.
From Fig.1(b),one can see that the solitons after splitting are asymmetric aboutx=0,which indicates that they have different propagating velocities. This kind of symmetry breaking also happens in the other cases of splitting dynamics. Thus,we define the asymmetry degree asv1/v2,wherev1andv2are the velocities of final solitons on the left-and right-hand sides,respectively. The values ofv1andv2are measured numerically by the ratio of space difference to the time difference of soliton center. Whenv1/v2=1,the two final solitons separate symmetrically aboutx=0. Conversely,v1/v2/=1 means that the two solitons have different velocities,always accompanied by the unequal of atom number. The influence of initial separationx0on the asymmetry degree is shown in Fig.3(a). The asymmetry degree distributes away from 1,which expresses as a gap around 1 in the plot. The similar result is also obtained whengdchanges, as shown in Fig.3(b). There is no obvious dependence between the asymmetry and the initial separation of the two solitons,and which soliton has the greater velocity seems to be random. We speculate that it is the accumulation of asymmetry in the soliton propagation that leads to the final splitting phenomenon.
When the strength of dipole–dipole interaction is large,the two solitons can form a breathing wave in Fig.1(c),whose periodTis defined as the time interval between its two adjacent peaks. The initial dipolar potential energy of solitons is consistent with the variation of initial separationx0. When thegdis fixed, the periodTkeeps constant approximately as illustrated in Fig. 3(c). Thus, the initial separation and the dipolar potential energy have no obvious effect on the period of breathing wave after merging.Furthermore,the influence ofgdonTis shown in Fig.3(d). The breathing period decreases with the increasinggd, which illustrates an approximative inversely proportional dependence between them.
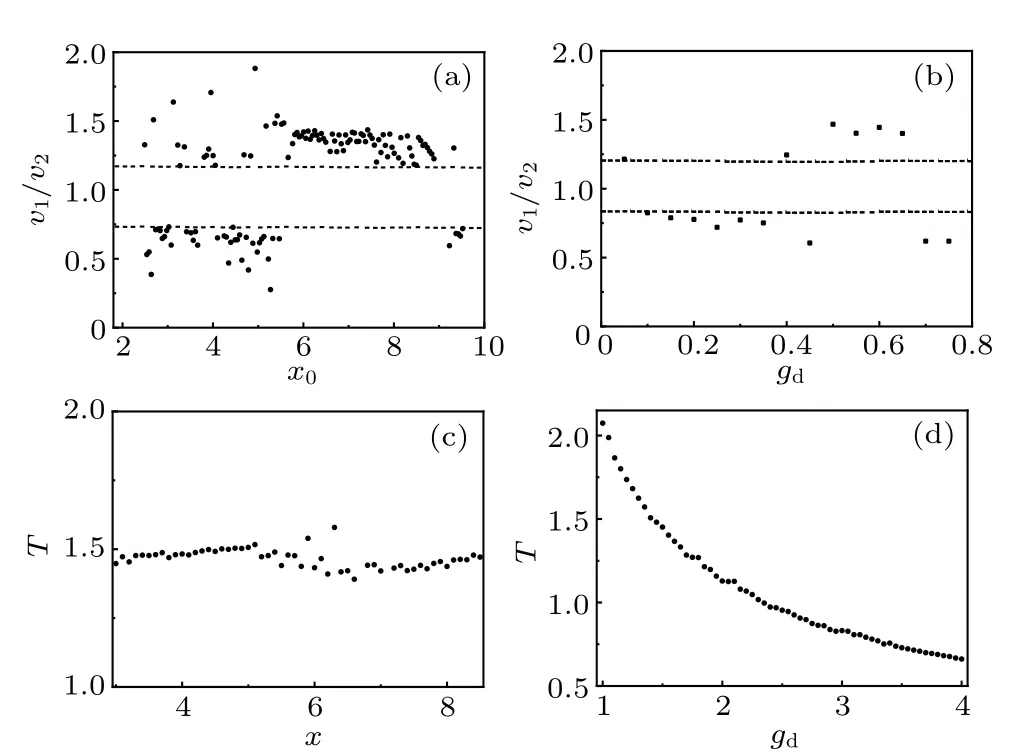
Fig.3. Influence of(a)x0 and(b)gd on the asymmetry degree v1/v2 in the cases of soliton splitting. We set gd=0.5 or x0=8 when the other one is changing. Influence of(c)x0 and(d)gd on the breathing period T in the cases of soliton merging. We set gd =1.2 or x0 =8 when the other one is changing.
In the interaction process between solitons,the consideration of their phase difference has brought many distinct effects.This prompts us to pay attention to the interaction dynamics between two dipolar solitons under different phase differences.When the solitons are in-phase, we severally study the cases
where the splitting or merging dynamics is induced.In the former case(i.e.,splitting),the splitting always occurs when we change the phase difference?. The two solitons express as a bound state with stable oscillating period when?reachesπ.In the latter case(i.e.,merging),the phase difference displays a more abundant influence.Figures 4(a)–4(d)show the density evolutions under several different?, and their corresponding evolutions of kinetic energy are depicted in Fig.4(e). We recall that,when?=0,the two solitons interact and merge,as shown in Fig. 4(c). Its kinetic energy firstly increases, then sharply falls and rebounds, when the solitons collide. Interestingly,the merging dynamics disappears when?is slightly increased. We show the density evolution of two solitons with?=0.01πin Fig. 4(a). They split asymmetrically after several oscillating periods, which indicates that the small phase difference brings instability to the original merging dynamics.Compared with the case of?=0, its kinetic energy gradually becomes different after the collision.When?is increased into 0.5π, the evolution plot is shown in Fig. 4(b), where the splitting happens. The evolution of kinetic energy becomes smoother than the last two cases. When?is close to but not equal toπ, although the splitting finally happens, there are several rebounds before it. As an example,the evolution plot is shown in Fig. 4(c) when?=0.9π. When?=π, the two solitons form a stable bound state, as illustrated in Fig. 4(d).The final two cases showcase smoothest evolution of kinetic energy. In a word, when the phase difference changes, there appear four kinds of interaction dynamics,including the merging, splitting, splitting after rebounds, and the bound state.With the phase difference increasing, the interaction between solitons illustrates more regular dynamics,and the transfer between its kinetic and interaction energies is flatter.

Fig. 4. (a)–(d) Density evolution plots of initial condition (2) when (a)? = 0.01π, (b) ? = 0.5π, (c) ? = 0.9π, and (d) ? = π. (e) Kinetic energy evolution of above four cases. The green, red, black, blue, and purple curves correspond respectively to the cases of ? =0,0.01π,0.5π,0.9π,and π (the blue curve is covered by the purple one). Other parameters are gc=1,gd=1.2,and x0=8.
In summary,we have illustrated the interaction results of two bright solitons with zero initial velocities in the dipolar BECs. Under the low strength of dipolar effect, the two solitons are asymmetrically splitting after colliding and oscillating for several periods. We characterize the splitting interaction by the asymmetric degree of final solitons. Obeying the law of momentum conservation,the splitting exhibits random and highly asymmetric results. After the strength of dipolar effect is increased,the two solitons may merge into a breathing wave with a stable oscillating frequency. The period of bound state declines with the increasing strength of dipole–dipole interaction and keeps invariable value under different initial separations of solitons. Moreover, the initial phase difference of solitons has an obvious effect on enriching the interaction dynamics. The bound state is formed when the solitons are outof-phase. There is a transition process between merging,splitting,and bound state when one changes the phase difference.
- Chinese Physics B的其它文章
- Modeling the dynamics of firms’technological impact?
- Sensitivity to external optical feedback of circular-side hexagonal resonator microcavity laser?
- Controlling chaos and supressing chimeras in a fractional-order discrete phase-locked loop using impulse control?
- Proton loss of inner radiation belt during geomagnetic storm of 2018 based on CSES satellite observation?
- Embedding any desired number of coexisting attractors in memristive system?
- Thermal and mechanical properties and micro-mechanism of SiO2/epoxy nanodielectrics?