Adaptive synchronization of a class of fractional-order complex-valued chaotic neural network with time-delay?
Mei Li(李梅) Ruo-Xun Zhang(張若洵) and Shi-Ping Yang(楊世平)
1College of Physics,Hebei Normal University,Shijiazhuang 050024,China
2Department of Computer Science,North China Electric Power University,Baoding 071003,China
3College of Primary Education,Xingtai University,Xingtai 054001,China
Keywords: adaptive synchronization,fractional calculus,complex-valued chaotic neural networks,time-delay
1. Introduction
In recent years, the theory of fractional calculus and its application have become a most intense research topics. Compared with traditional integer calculus,fractional calculus and related models can better describe certain actual physical systems and capture their essential properties and behaviors. So far, it has generally become an efficient tool in physics, artificial intelligence, mathematical science, chemical engineering science, control engineering science, optimization combination, material science, electronic information, digital signal processing, cognitive science, and other fields.[1–6]Some interesting results about the dynamic behaviors of fractionalorder systems have been derived.[7–16]Thus, the study of the theory and applications of nonlinear fractional-order differential systems are of high theoretical and significant practical importance.
Complex-valued neural networks (CNNs) are the progressive forms of real-valued neural networks(RNNs). Compared with RNNs, the CNNs have the advantages of simple network structure, concise training process, and strong ability to handle complex signals, which can be used to solve problems that cannot be solved by real-valued neural networks. Hence, it is widely used in physical systems dealing with electromagnetic, optical, ultrasonic, and quantum waves as well as in fields such as filtering, speech synthesis, and remote sensing. Owing to the memorability and heritability of fractionalorder models,fractional calculus is combined into complex-valued neural networks to form fractionalorder complex-valued neural network models, which further expands the basic theory and application capability of neural networks.
Over the last few years, the dynamical behaviors, stability analysis and synchronous control of neural networks have become an area of particular interest and active research,and some excellent outcomes have been achieved.[17–28]For instance in Refs. [17,18], the projection synchronization and adaptive synchronization of fractional-order memristor neural networks were discussed. In Ref. [19], the synchronization of fractional-order complex-valued neural networks (FOCVNNs) was studied with linear delay feedback control. In Refs. [20–22] the global Mittag–Leffler synchronization of fractional-order neural networks was investigated. In Refs.[23–28], the the stability, finite-time stability,and global Mittag–Leffler stability of fractional-order timedelayed complex-valued neural networks were analyzed, respectively. Most of the literature in this area, however, was devoted to the study of stability analysis and periodic oscillations of various neural networks, only a few researches was involved with the study of fractional-order complex-valued chaotic neural networks (FOCVCNNs). However, the engineering applications of chaotic systems have been studied widely and intensively in recent years.[29–31]Furthermore,fractional-order complex-valued chaos can generate complex and unpredictable dynamic behaviors,which will enhance resistance to attacks,and achieve higher transmission efficiency in secure communications.This property extensively broadens the application of fractional-order neural networks. Owing to the limited speed of signal transmission between neurons,delays usually occur in neural networks. The time delays will affect or even destroy the dynamic properties of neural networks. Nevertheless, to the best of our knowledge, there are very few studies on the chaotic dynamics of fractional-order complex-valued neural networks with time delays. Based on the above discussion, this paper is to investigate the chaos in FOCVCNNs and the synchronization problems of FOCVCNNs. Fractionalorder complex variable differential inequalities,stability theory and adaptive control methods for fractionalorder complex-valued systems are used in order to achieve the synchronization of FOCVCNNs.
2. Problem formulation and preliminaries
In this section,we first address some definitions and theorems about fractional calculus.
Definition 1[1]The fractional-order integral of a functionfis defined as

3. Main results
3.1. Model description
We consider a class of FOCVCNN described by the following equations:
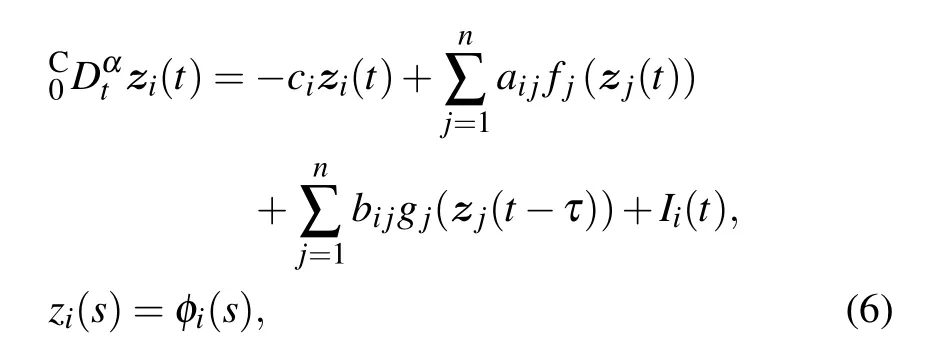
wheret ≥0,i=1,2,...,n,s ∈[?τ,0],0<α<1,zi(t)∈C is the complex variable of thei-th neuron at timet,fj(·),gj(·)∈C denote the activation functions without and with timedelay,ai j,bi j ∈C represent the connection weights and delayed connection weights respectively,ci ∈R,τ>0 are the constant delay times,Iidenotes the corresponding external input. The complex-valued functionsfj(·),gj(·)andIisatisfy the following assumptions.

Fig.1. Dynamic behaviors of FOCVNN(7),showing(a)maximal Lyapunov exponents and(b)bifurcation diagram.
Assumption 1 For anyμ,ν ∈C,there exist real numberslj,hj>0 that satisfy the following inequalities:

Assumption 2 For anyv ∈C, there exist real numbersγi>0 andεi>0 that satisfy the following inequalities|fj(ν)|≤γiand|Ii(ν)|≤εi.
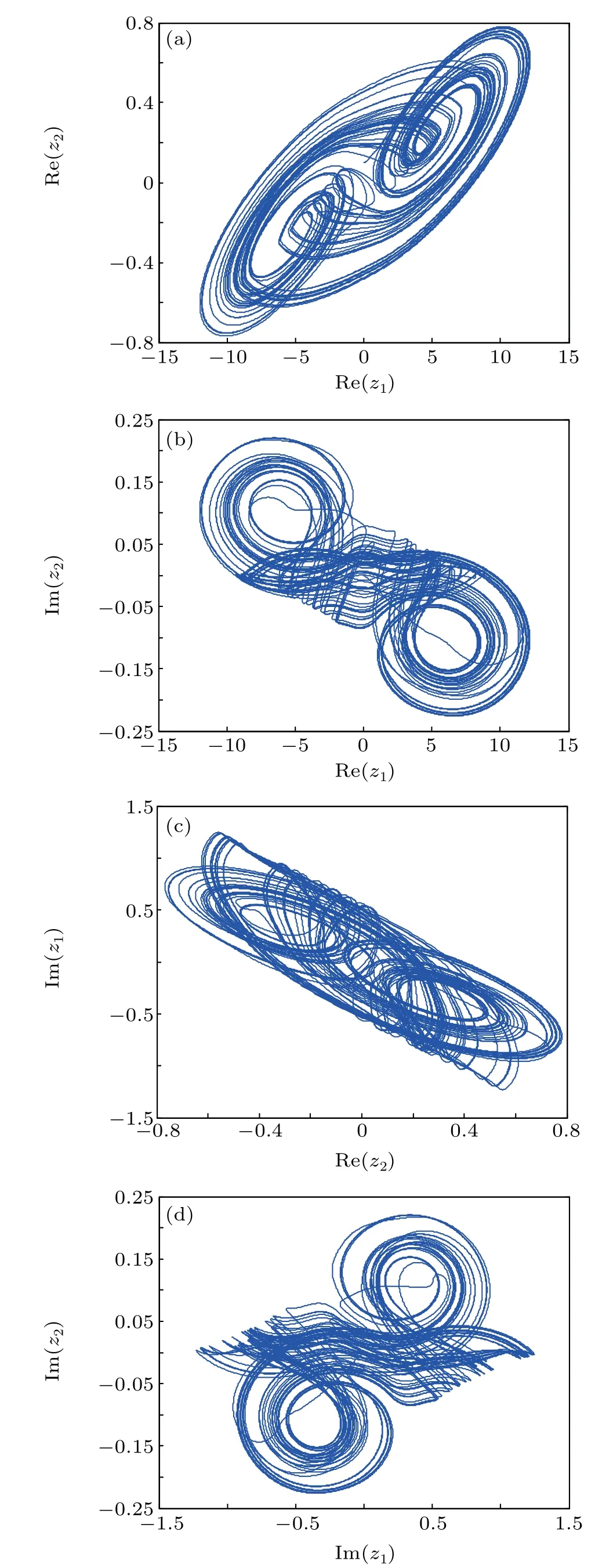
Fig.2. Chaotic attractors of FOCVCNN(7),showing(a)Re(z1)–Re(z2),(b)Re(z1)–Im(z2),(c)Re(z2)–Im(z1),and(d)Im(z1)–Im(z2).
Equation system (6) can exhibit chaotic behaviors if appropriate network parameters and delay times are chosen. We consider the following FOCVCNN:
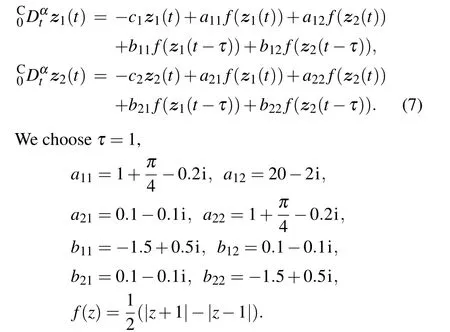
The maximum Lyapunov exponent(MLE)spectrum is shown in Fig. 1(a), and the bifurcation diagram is presented in Fig.1(b). From Figs.1(a)and 1(b), it can be seen that equation system(7)is chaotic when the fractionalorder is at some specific values. Figure 2 shows the chaotic attractor trajectory of each complex state quantity of system(7)whenα=0.96,which also verifies the correctness of the above conclusion.
3.2. Adaptive synchronization of fractional-order complex-valued chaotic neural networks
System (6) is chosen as a master system and the controlled response system is described by

wheret ≥0,i=1,2,...,n,s ∈[?τ,0],wi(t)∈C is the complex variable of thei-th neuron of the response system, andu(t)=(u1(t),u2(t),...,un(t))Tis the controller to be determined.
The synchronization error between master system(6)and slave system (8) can be written asei(t)=wi(t)?zi(t). The fractional-order error dynamic system is determined from the following equation:

wherei=1,2,...,n.
The adaptive laws are as follows:
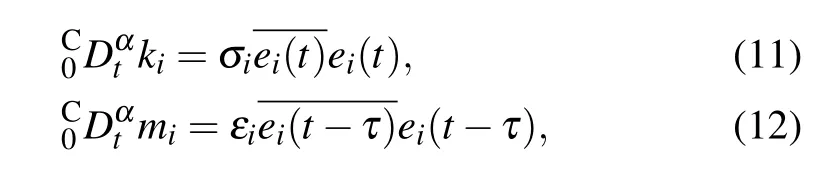
whereσiandεiare the positive constants.
Proof The Lyapunov candidate functions can be presented by
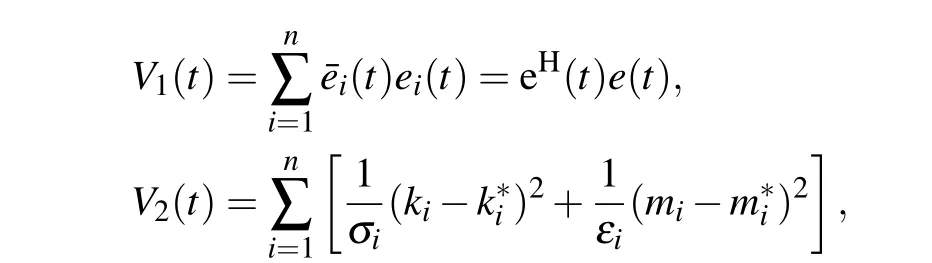
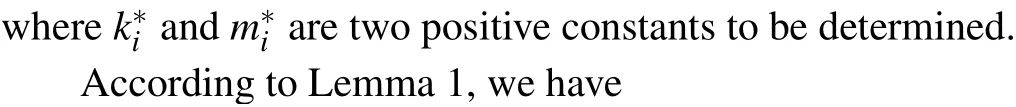

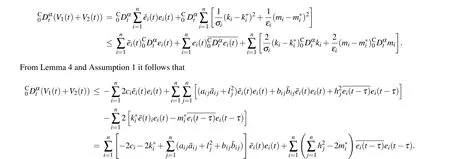
Remark 2 According to previous researches in Refs.[27,37,38], a common approach to analyzing the fractionalorder complex-valued neural networks is to decompose the complex-valued neural network into two fractional-order realvalued neural networks according to their real part and imaginary part, and then obtain a criterion about synchronization by investigating these real-valued neural networks. Unfortunately, there are two disadvantages in this approach. First,the dimensionality of the real-valued neural network is twice that of the complex-valued neural network,thereby increasing the complexity of computation and analysis. Moreover, not all complex functions can be divided into real part and imaginary part in practical applications.Unlike previous researches,the whole analysis process is performed in the complex-valued domain in our proposed method. The synchronization conditions are derived by using the complex function theory, without dividing the original complex-valued neural network into two real-valued networks,which effectively reduces the complexity of analysis and computation. In addition,the proposed method can be applied to other complex-valued systems,such as fractional-order complex-valued chaotic systems.
Remark 3 Compared with feedback control, adaptive control in this paper can automatically adjust the certain parameters of system to accomplish synchronization, thereby greatly reducing the control cost.
4. Numerical simulations
In this section, numerical simulations of fractional-order complex-valued chaotic neural network (FOCVCNNs) synchronization is provided in order to demonstrate the validity of the previously proposed scheme. We use the predictioncorrection method to numerically solve these problems.[38]The FOCVCNN(7)is selected as the driving system,and the controlled response system is described as follows:

Let the synchronization error beei(t) =wi(t)?zi(t),(i=1,2) and according to Theorem 1, the controller is selected as


Fig. 3. Synchronization errors of fractional-order complex-valued chaotic neural networks with control parameters σi=εi=6(i=1,2)for(a)Re(e1)and Im(e1),and(b)Re(e2)and Im(e2).
The numerical results are depicted in Fig. 3, indicating that error dynamic system (9) converges to zero. The drive system (7) and response system (13) can be asymptotically synchronized under the action of the adaptive controller(10).The simulation results confirm the effectiveness of the proposed scheme.
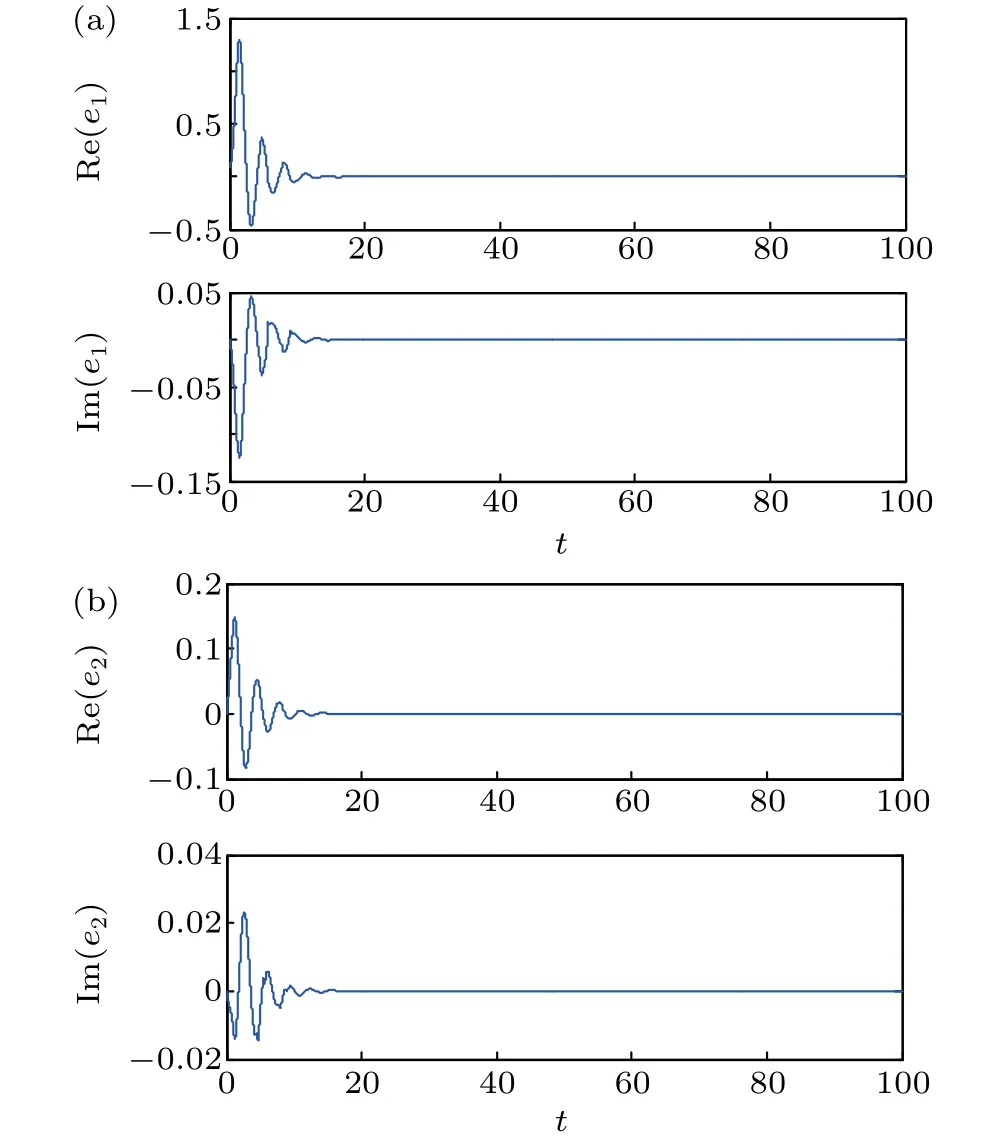
Fig. 4. Synchronization errors of fractional-order complex-valued chaotic neural networks with control parameters σi=εi=1(i=1,2)for(a)Re(e1)and Im(e1),and(b)Re(e2)and Im(e2).
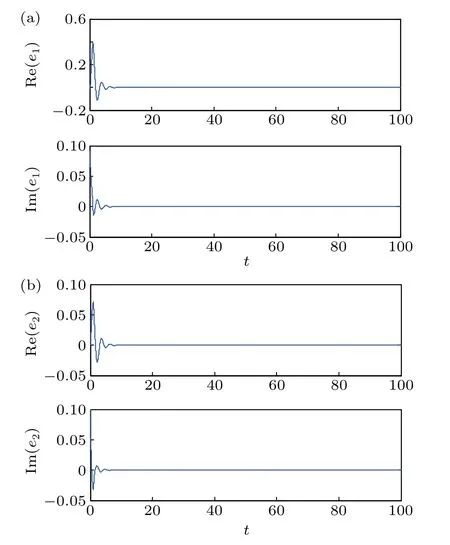
Fig. 5. Synchronization errors of fractional-order complex-valued chaotic neural networks with control parameters σi =εi =20(i=1,2) σi =εi =6(i=1,2)for(a)Re(e1)and Im(e1),and(b)Re(e2)and Im(e2).
In order to investigate the synchronization performance of the proposed method,numerical simulations are conducted by setting the control parameters to beofσi=εi=1(i=1,2)andσi=εi=10(i=1,2),respectively. The synchronization results are shown in Figs.4 and 5,indicating that the increasing of the control parameters can speed up the synchronization of system, but the synchronization parameters should not be too large or too small. In addition,through the simulation,we find that when the control parameters are set to beεi=0,the two systems can still achieve synchronization. We will further attests to this in our future research work.
5. Conclusion
In this paper, the synchronization problem of fractionalorder complex-valued chaotic neural networks is discussed.The chaotic behaviors of a class of fractional-order complexvalued neural network are investigated, and the synchronization of FOCVCNNs is accomplished in the complex domain by an adaptive controller. The effectiveness of the proposed scheme is further confirmed by numerical simulations. In the future research, we will study the synchronization problem of fractional-order complex-valued chaotic neural networks with external disturbances and unknown parameters. We will also further investigate how to implement this synchronization scheme with actual circuits and how to apply it to the secure communication.
Acknowledgment
The authors thank other people or groups for their scientific contributions to this work.
- Chinese Physics B的其它文章
- Modeling the dynamics of firms’technological impact?
- Sensitivity to external optical feedback of circular-side hexagonal resonator microcavity laser?
- Controlling chaos and supressing chimeras in a fractional-order discrete phase-locked loop using impulse control?
- Proton loss of inner radiation belt during geomagnetic storm of 2018 based on CSES satellite observation?
- Embedding any desired number of coexisting attractors in memristive system?
- Thermal and mechanical properties and micro-mechanism of SiO2/epoxy nanodielectrics?