帶連續(xù)變彎度后緣操縱面機翼的動態(tài)失速減緩
歐陽炎 ,寇西平 ,,郭洪濤 ,楊智春
(1.西北工業(yè)大學(xué)結(jié)構(gòu)動力學(xué)與控制研究所,西安710072)
(2.中國空氣動力研究與發(fā)展中心高速空氣動力研究所,綿陽621000)
0 引 言
動態(tài)失速是包含一系列流動分離、失速延遲的非定常流動現(xiàn)象,通常在翼型攻角大幅超過靜態(tài)失速攻角范圍,且隨時間周期性變化或者急劇增大的情況下發(fā)生。發(fā)生動態(tài)失速時,翼型表面動態(tài)失速渦的發(fā)展和運動將使翼型的氣動力系數(shù)極值顯著超過定常流動時的情況。機翼可能出現(xiàn)升力驟降、阻力激增、結(jié)構(gòu)振動幅值增大甚至誘發(fā)失速顫振,嚴(yán)重影響飛行安全,因此關(guān)于動態(tài)失速的研究一直是航空領(lǐng)域關(guān)注的熱點。直升機槳葉翼型負(fù)的俯仰力矩(低頭力矩)極值決定了槳葉根部變距拉桿的結(jié)構(gòu)強度設(shè)計要求,減小動態(tài)失速時翼型負(fù)的俯仰力矩系數(shù)極值對于直升機槳葉而言意義重大。
發(fā)生動態(tài)失速時的脫體渦通常起源于翼型前緣,因此各種前緣裝置最早被用來減緩動態(tài)失速。典型的研究工作包括:改變前緣半徑和厚度,采用變彎度前緣操縱面、前緣縫翼、微型擾流片以及前后緣聯(lián)合射流。由于直升機槳葉翼型前緣通常會面臨復(fù)雜的流動情況,且前緣的變化通常會引起較大的翼型重心位置移動,故前緣控制方法在槳葉上應(yīng)用比較困難。槳葉后緣部分通常結(jié)構(gòu)相對簡單且有較大的操作空間,采用后緣控制的方法逐漸受到研究者們的青睞。
D.Feszty 等利用離散渦方法研究了剛性后緣操縱面減緩翼型動態(tài)失速特性,發(fā)現(xiàn)正弦脈沖偏轉(zhuǎn)信號能有效減小低頭力矩系數(shù)的極值;R.B.Green 等在風(fēng)洞實驗中驗證了 D.Feszty 等的結(jié)論,并提出了一種稍加改進(jìn)的偏轉(zhuǎn)控制信號;P.Gerontakos 等開展了一系列風(fēng)洞實驗,提出一種類似梯形波的偏轉(zhuǎn)方案,同樣取得了很好的控制效果。國內(nèi),馬奕揚等利用CFD 方法,分析了正弦偏轉(zhuǎn)信號中頻率和相位對動態(tài)失速減緩效果的影響;王榮等利用沿展向分布的三個操縱面減小了槳轂的振動載荷;劉洋等發(fā)現(xiàn)操縱面和主翼之間的縫隙大于弦長的6%時,剛性后緣操縱面偏轉(zhuǎn)時的前緣突起會降低減緩效果。
從上述文獻(xiàn)可以看出,人們在利用剛性后緣操縱面減緩動態(tài)失速方面進(jìn)行了較為深入的研究,而采用連續(xù)變彎度后緣操縱面進(jìn)行動態(tài)失速減緩的研究比較少見。剛性操縱面在偏轉(zhuǎn)后,中弧線仍是直線形狀,而連續(xù)變彎度后緣操縱面在偏轉(zhuǎn)后中弧線呈曲線形狀。操縱面彎度的連續(xù)變化是變體機翼分類中的沿弦向變體。
楊智春等在研究機翼的定常氣動特性時發(fā)現(xiàn),和剛性操縱面相比,連續(xù)變彎度后緣操縱面在增加升力的同時會帶來更大的低頭力矩;吳優(yōu)等計算了翼型攻角大幅度俯仰振蕩時的非定常氣動特性,發(fā)現(xiàn)連續(xù)變彎度后緣操縱面能顯著提升翼型的升力并降低阻力;Zhuang C 等利用連續(xù)變彎度后緣操縱面提高風(fēng)力機葉片在一個運動周期內(nèi)的平均升力并減小阻力。由此可知,連續(xù)變彎度后緣操縱面在減緩翼型動態(tài)失速方面有極大的應(yīng)用潛力,有必要開展深入的研究。
在已有的研究工作中,不管是采用前緣操縱面還是后緣操縱面,都很少考慮驅(qū)動操縱面偏轉(zhuǎn)所需的能量輸入。由于驅(qū)動系統(tǒng)設(shè)計是變體機翼的關(guān)鍵技術(shù)之一,本文將連續(xù)變彎度操縱面的能量輸入需求作為重要的性能指標(biāo)進(jìn)行考慮。采用CFD 的方法,研究利用連續(xù)后緣操縱面減緩翼型動態(tài)失速的可行性;通過與傳統(tǒng)剛性操縱面對比,分析后緣操縱面的彎度構(gòu)型對動態(tài)失速減緩效果的影響;從減緩效果和能量輸入需求兩個方面,得到最佳的連續(xù)變彎度后緣操縱面構(gòu)型。
1 連續(xù)變彎度操縱面的定義
等效偏轉(zhuǎn)角定義如圖1 所示,傳統(tǒng)剛性操縱面(實線)偏轉(zhuǎn)時,將繞著鉸鏈轉(zhuǎn)軸(x
,0)點作剛體旋轉(zhuǎn)運動,旋轉(zhuǎn)角度β
即為操縱面的偏轉(zhuǎn)角度。連續(xù)變彎度操縱面(虛線)沒有一個所謂的轉(zhuǎn)軸點。為了定量描述連續(xù)變彎度操縱面的偏轉(zhuǎn)程度,基于翼型后緣點的垂直位移,定義一個等效偏轉(zhuǎn)角,該角度與具有同樣弦長和后緣點位移的剛性操縱面偏轉(zhuǎn)角相等。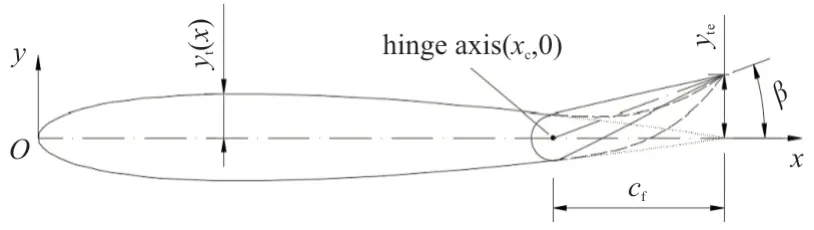
圖1 等效偏轉(zhuǎn)角定義Fig.1 Definition of equivalent deflection angle
圖1 中,弦長為c
的剛性操縱面向上偏轉(zhuǎn)時后緣點的垂直位移為y
,則連續(xù)變彎度操縱面的等效偏轉(zhuǎn)角為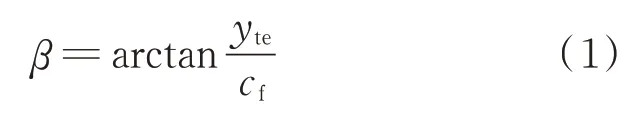
即圖中的兩種操縱面具有相同的偏轉(zhuǎn)角。
采用式(2)來統(tǒng)一描述后緣操縱面偏轉(zhuǎn)后的中弧線:
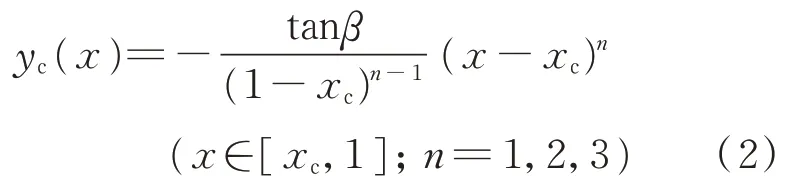
n
為多項式的階數(shù),決定了操縱面的類型。當(dāng)n
=1 時,為剛性操縱面;當(dāng)n
等于 2 或 3 時,為連續(xù)變彎度操縱面。本文以多項式的階數(shù)來代稱連續(xù)變彎度操縱面,如2 階操縱面指的是n
=2 時的連續(xù)變彎度操縱面,以便于理解和計算。單位弦長的NACA 四位數(shù)翼型的厚度分布函數(shù)y
(x
)定義如下:
t
為翼型的無量綱最大厚度(如t
=0.12 時即是NACA 0012);x
∈[0,1]為無量綱弦向位置。假定操縱面在偏轉(zhuǎn)前后的厚度分布保持不變,那么操縱面上翼面(x
,y
)和下翼面(x
,y
)的位置坐標(biāo)可按式(4)計算: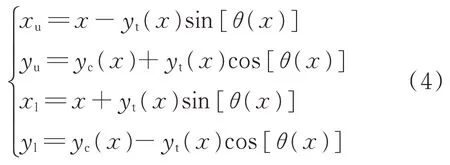
θ
(x
)為中弧線函數(shù)的斜率。
n
和偏轉(zhuǎn)角β
確定后,根據(jù)式(2)~式(4)便可計算整個翼型上下翼面的坐標(biāo)。NACA 0012 干凈翼型和三種后緣操縱面構(gòu)型如圖2 所示,根據(jù)等效偏轉(zhuǎn)角的定義,圖2(b)~圖2(d)中三種后緣操縱面的偏轉(zhuǎn)角相等。剛性操縱面偏轉(zhuǎn)后,上下翼面在轉(zhuǎn)軸位置處有明顯的轉(zhuǎn)折點,而兩種連續(xù)變彎度操縱面的翼型表面能始終保持光滑連續(xù),且3 階操縱面比2 階操縱面彎度的曲率大。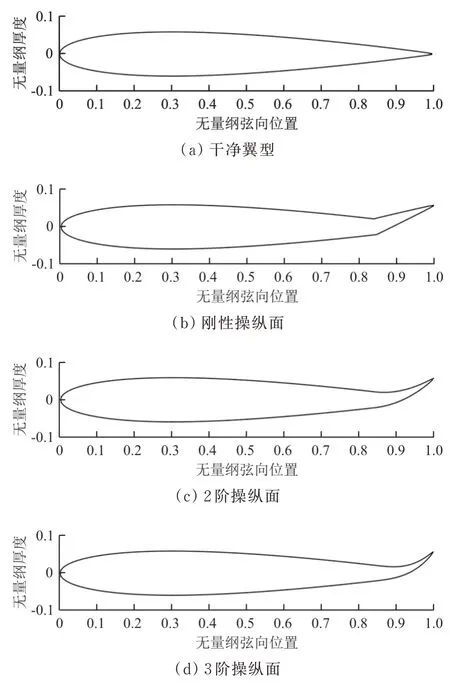
圖2 NACA 0012 干凈翼型和三種后緣操縱面構(gòu)型(β=20°)Fig.2 Baseline NACA 0012 and airfoils with different kinds of flap(β=20°)
在工程實際中,剛性操縱面和主翼之間會留有縫隙,即蒙皮在轉(zhuǎn)軸處不連續(xù)。因為本文主要關(guān)注操縱面彎度的影響,所以在計算過程中假定剛性操縱面在偏轉(zhuǎn)后蒙皮仍保持連續(xù)。作動機構(gòu)驅(qū)動剛性操縱面在氣流中偏轉(zhuǎn)時,需要平衡操縱面所承受的氣動載荷,剛性操縱面的鉸鏈力矩可以作為衡量驅(qū)動能量輸入的指標(biāo)。對于連續(xù)變彎度操縱面而言,沒有所謂的轉(zhuǎn)動軸。為了進(jìn)行對比分析,在計算過程中將連續(xù)變彎度操縱面上的氣動載荷對操縱面偏轉(zhuǎn)起始點進(jìn)行積分求力矩,并仍稱之為鉸鏈力矩,以方便敘述。
2 數(shù)值計算方法
2.1 控制方程和求解器
為了模擬非定常流動中的分離和動態(tài)失速渦,采用基于雷諾平均的N-S 方程作為流場的控制方程:
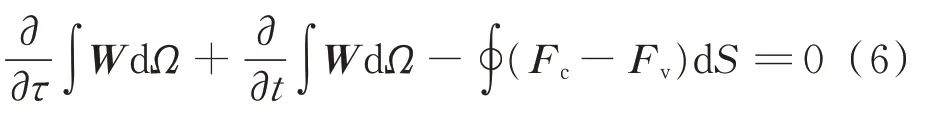
W
=[ρ
,ρv
,ρv,e
],為守恒變量向量,其中,ρ
為空氣密度,v
和v
分別為速度沿x
軸和y
軸的分量,e
為總能量;τ
和t
分別為偽時間和物理時間;Ω
為流場單元體積;S
為流場單元邊界;F
和F
分別為對流通量項和黏性通量項。在求解N-S 方程模擬動態(tài)失速的大攻角非定常瞬態(tài)流動時,需選擇合適的湍流模型以保證計算結(jié)果的精度。J.A.Ekaterinaris 等對早期的動態(tài)失速模擬中的數(shù)值方法進(jìn)行了詳細(xì)總結(jié)。在已有的各種湍流模型中,SSTk-ω
模型使用比較廣泛,在預(yù)測失速攻角和計算氣動力方面都有較好的計算精度和效率。本文在商業(yè)軟件Fluent中,利用壓力基求解器結(jié)合SSTk
-ω
湍流模型求解方程(6),計算翼型動態(tài)失速過程中的氣動力和流場特性。2.2 動網(wǎng)格
在翼型俯仰振蕩和后緣操縱面的主動偏轉(zhuǎn)過程中,翼型表面的邊界位置會按指定規(guī)律運動。在Fluent 軟件中,可以采用動網(wǎng)格技術(shù)來模擬翼型邊界的運動。由于不涉及結(jié)構(gòu)的彈性變形,本文計算過程中的主翼和操縱面的運動直接由自定義函數(shù)(UDF)給定。采用擴散光順?biāo)惴ǎM量讓遠(yuǎn)場的網(wǎng)格產(chǎn)生變形,保留翼型近壁面區(qū)域的網(wǎng)格形態(tài),確保網(wǎng)格更新后無量綱壁面距離y
滿足要求。當(dāng)后緣操縱面偏轉(zhuǎn)角β
=20°時,網(wǎng)格動態(tài)更新后的結(jié)果如圖3 所示,可以看出:變形后的網(wǎng)格質(zhì)量保持良好。
圖3 NACA 0012 干凈翼型和帶不同操縱面構(gòu)型網(wǎng)格動態(tài)變化結(jié)果Fig.3 Dynamic grid deformation for NACA 0012 airfoil and three kinds of flaps
2.3 數(shù)值算例
采用與文獻(xiàn)[11]相同的翼型和流動工況,將本文CFD 計算結(jié)果與文獻(xiàn)[11]中的風(fēng)洞實驗數(shù)據(jù)進(jìn)行對比,以驗證N-S 方程求解器和動網(wǎng)格的計算結(jié)果精度。不帶操縱面的NACA 0012 干凈翼型以減縮頻率k
=0.173 繞四分之一弦長點進(jìn)行俯仰振蕩,來流馬赫數(shù)Ma
=0.117,雷諾數(shù)Re
=1.463 296×10。攻角隨時間的變化規(guī)律為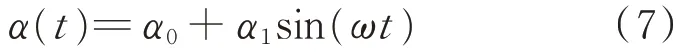
α
=15°;攻角振蕩幅值α
=10°。無量綱角頻率ω
為
v
為來流速度;b
為 0.5 倍弦長。流場計算所用C 型網(wǎng)格如圖4 所示。通過設(shè)置來流方向,使得當(dāng)翼型水平放置時,攻角α
=15°。對翼型近壁面網(wǎng)格進(jìn)行加密處理,通過設(shè)置第一層網(wǎng)格高度確保無量綱壁面距離滿足y
≈1.0。利用由疏到密的三套網(wǎng)格(G1、G2 和 G3)進(jìn)行網(wǎng)格收斂性驗證,三套網(wǎng)格包含的單元數(shù)目分別為50 160、75 400 和100 800。計算得到的氣動力系數(shù)隨攻角的變化曲線如圖5 所示,圖中的箭頭為時間推進(jìn)方向。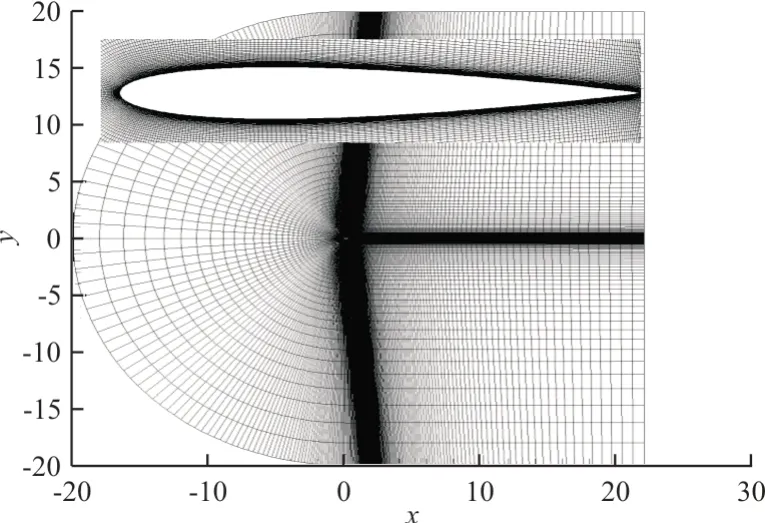
圖4 遠(yuǎn)場網(wǎng)格以及翼型局部放大圖Fig.4 The C-type mesh and zoomed view of the NACA 0012 airfoil


圖5 干凈翼型俯仰振蕩時氣動力系數(shù)時滯曲線Fig.5 Aerodynamics loops for oscillating
從圖5 可以看出:中等網(wǎng)格G2 和加密網(wǎng)格G3的計算結(jié)果非常接近,在后續(xù)的計算中采用G2 網(wǎng)格即可兼顧計算精度和效率;對于升力系數(shù)曲線,本文的計算結(jié)果和實驗結(jié)果吻合較好;對于力矩系數(shù)曲線,在翼型攻角上行階段,本文的仿真結(jié)果與實驗結(jié)果吻合較好,在攻角下行階段則略有差別。E. Guilmineau 等也闡述了同樣的差別,并指出可能是因為CFD 方法過高地估計了動態(tài)失速渦脫落造成的吸力。
無量綱的氣動阻尼系數(shù)作為指標(biāo)來衡量翼型在一個俯仰振蕩周期內(nèi)從氣流中吸收的總能量,由俯仰力矩系數(shù)對攻角進(jìn)行封閉曲線積分計算得到:

則在圖5(b)俯仰力矩系數(shù)曲線中,左側(cè)逆時針方向的小閉環(huán)意味著正的氣動阻尼,右側(cè)順時針方向的小閉環(huán)則對應(yīng)負(fù)的氣動阻尼。如果保持俯仰力矩系數(shù)曲線的基本形狀不變,減小負(fù)的俯仰力矩系數(shù)極值,也可能會減小順時針小閉環(huán)圍成的面積,進(jìn)而減小整個運動周期的負(fù)氣動阻尼。
3 操縱面偏轉(zhuǎn)策略
利用占機翼總弦長16%的剛性后緣操縱面,按照正弦脈沖信號向上偏轉(zhuǎn),可以有效地減小動態(tài)失速時的負(fù)俯仰力矩系數(shù)極值。該脈沖信號的表達(dá)式為
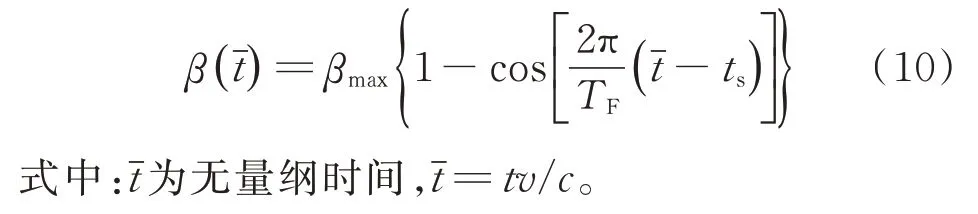
β
、偏轉(zhuǎn)起始時刻t
以及持續(xù)時間T
。
圖6 正弦脈沖式偏轉(zhuǎn)信號Fig.6 Pulse deflection signal profile
文獻(xiàn)[11]通過一系列的變參分析,在保持升力特性和減緩動態(tài)失速兩方面進(jìn)行了綜合考慮,得出了最優(yōu)控制規(guī)律的系數(shù)為:β
=20°,t
=2.2,T
=6。本文采用與此相同的偏轉(zhuǎn)控制規(guī)律,對比研究不同類型操縱面減緩動態(tài)失速的效果。4 結(jié)果與討論
4.1 動態(tài)失速減緩時的氣動力系數(shù)分析
采用上一節(jié)中描述的控制規(guī)律進(jìn)行動態(tài)失速減緩后,帶不同后緣操縱面翼型的氣動力系數(shù)如圖7 所示。為了加深對動態(tài)失速特性的理解,圖中也加入了干凈翼型的定常氣動力系數(shù)曲線。


圖7 不同類型操縱面動態(tài)失速減緩效果Fig.7 Comparison of dynamics stall control by different kinds of flaps
從圖7(a)可以看出:對于干凈翼型而言,當(dāng)α
= 16.00°時將發(fā)生靜態(tài)失速,而發(fā)生動態(tài)失速時,升力失速則被顯著推遲到更大的攻角下,這是動態(tài)失速的一個典型特征。在翼型攻角上行的初始階段,操縱面還沒有開始偏轉(zhuǎn),升力系數(shù)隨著攻角的增大而線性增大。當(dāng)α
= 24.96°↑時(↑和↓分別代表上行和下行方向),干凈翼型的升力系數(shù)達(dá)到最大,此時的升力系數(shù)比定常條件下的最大升力系數(shù)值大73.4%。當(dāng)α
=21.90°↑時,操縱面開始向上偏轉(zhuǎn)。三個帶操縱面翼型的升力系數(shù)先減小后增大,升力系數(shù)極值小于干凈翼型的情況。在攻角下行的大部分階段,操縱面偏轉(zhuǎn)將造成不同程度的升力損失。好在這種升力損失對于直升機槳葉翼型而言并非致命缺陷,因為在高速飛行時,槳葉產(chǎn)生的升力大部分源自外側(cè)65%~85%展向位置區(qū)域。從圖7(b)可以看出:相對于干凈翼型而言,后緣操縱面的偏轉(zhuǎn)顯著減小了負(fù)的俯仰力矩系數(shù)的極值。3 階操縱面和剛性操縱面的減緩效果非常接近,2 階操縱面的減緩效果最好,能將俯仰力矩負(fù)的極值進(jìn)一步減小。操縱面偏轉(zhuǎn)之后,右側(cè)順時針的小閉環(huán)曲線的面積也明顯減小,對于實際的直升機槳葉結(jié)構(gòu)而言,這意味著從氣流中吸收的能量有所減少,降低了槳葉發(fā)生失速顫振的風(fēng)險,有利于減小結(jié)構(gòu)的振動幅值。
盡管阻力特性不是本文的研究重點,但是從圖7(c)可以看出:后緣操縱面偏轉(zhuǎn)后,翼型的阻力相對于干凈翼型有不同程度的下降,且最大阻力系數(shù)下降明顯。這說明使用后緣操縱面進(jìn)行動態(tài)失速減緩時,不會造成阻力增大。
從圖7(d)可以看出:在三種操縱面上行偏轉(zhuǎn)階段,鉸鏈力矩系數(shù)很小且變化緩慢。在下行偏轉(zhuǎn)階段,當(dāng)偏轉(zhuǎn)角小于15.00°↓之后,鉸鏈力矩系數(shù)值迅速減小,即作動機構(gòu)需要提供越來越大的作動力才能讓操縱面按照信號指令偏轉(zhuǎn)。當(dāng)偏轉(zhuǎn)角小于10.00°↓之后,鉸鏈力矩系數(shù)將達(dá)到極值。
綜上所述,在相同的偏轉(zhuǎn)策略下,驅(qū)動2 階操縱面的能量需求是最小的。
盡管文獻(xiàn)[11]中的偏轉(zhuǎn)規(guī)律僅對剛性后緣操縱面而言是最優(yōu)的,但連續(xù)變彎度操縱面在相同的偏轉(zhuǎn)規(guī)律下表現(xiàn)出了更好的減緩效果。可以預(yù)見,如果采用合適的優(yōu)化算法得到連續(xù)變彎度操縱面的最優(yōu)偏轉(zhuǎn)規(guī)律,那么利用連續(xù)變彎度后緣操縱面進(jìn)行動態(tài)失速減緩的效果將會有更進(jìn)一步的提升。
圖7 中涉及的氣動力系數(shù)極值以及按照公式(9)計算得到的一個運動周期內(nèi)的氣動阻尼系數(shù)如表1 所示。
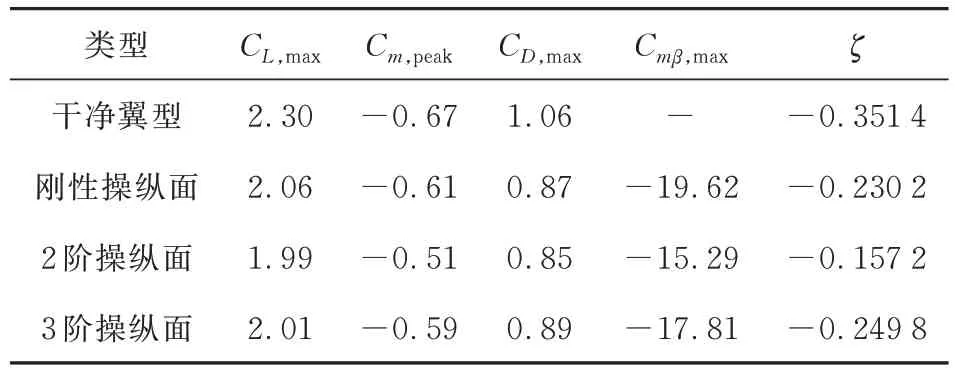
表1 帶不同類型操縱面翼型的關(guān)鍵性能參數(shù)Table 1 Key parameters of different kinds of flaps
從表1 可以看出:三種操縱面偏轉(zhuǎn)造成的升力損失基本處于同一水平;與干凈翼型相比,剛性操縱面和3 階操縱面可將負(fù)的俯仰力矩系數(shù)極值分別減小8.96%和11.94%,而2 階操縱面的減小量達(dá)到23.88%,減緩效果最為明顯;操縱面偏轉(zhuǎn)后,翼型的最大阻力至少會下降16.04%;在偏轉(zhuǎn)過程中,連續(xù)變彎度操縱面所承受的氣動載荷要小于剛性操縱面的情況,這對連續(xù)變彎度操縱面尤其是2 階操縱面的內(nèi)部結(jié)構(gòu)設(shè)計而言是一個潛在的優(yōu)勢;剛性操縱面、2 階和3 階操縱面偏轉(zhuǎn)后,翼型的負(fù)氣動阻尼將分別減少34.49%、55.26% 和28.91%。綜上所述,利用2 階操縱面減緩翼型動態(tài)失速的效果最好。
4.2 動態(tài)失速減緩時的流場分析
為了分析翼型發(fā)生動態(tài)失速時的流場細(xì)節(jié),研究后緣操縱面偏轉(zhuǎn)減緩動態(tài)失速的機理,通過流場的壓力系數(shù)云圖和流線圖來追蹤動態(tài)失速發(fā)生前后的一系列非定常流動現(xiàn)象。一些典型時刻的流場結(jié)果如圖8 所示,在每一時刻,首先關(guān)注干凈翼型的流場,然后分析后緣操縱面偏轉(zhuǎn)造成的影響,對比操縱面彎度產(chǎn)生的差異。
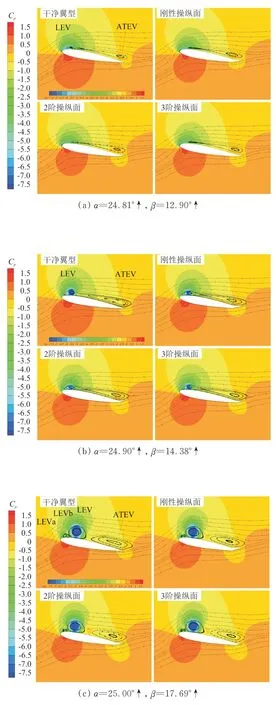
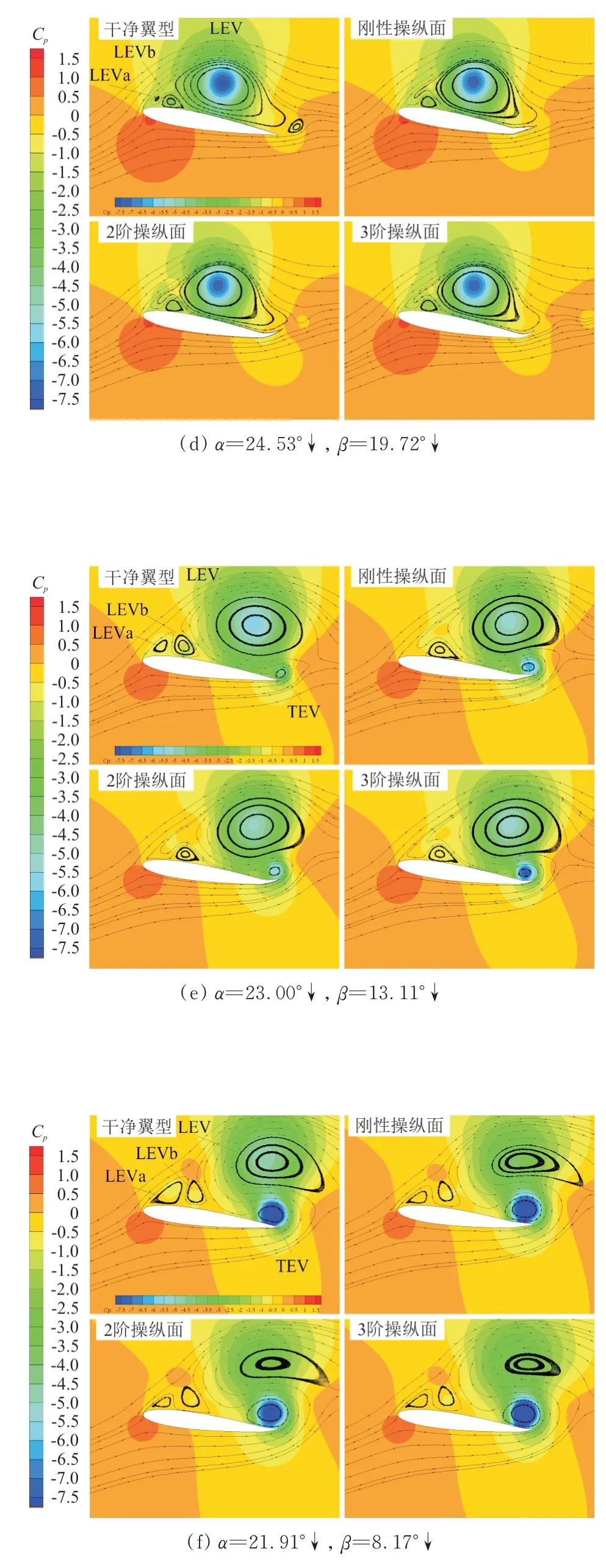
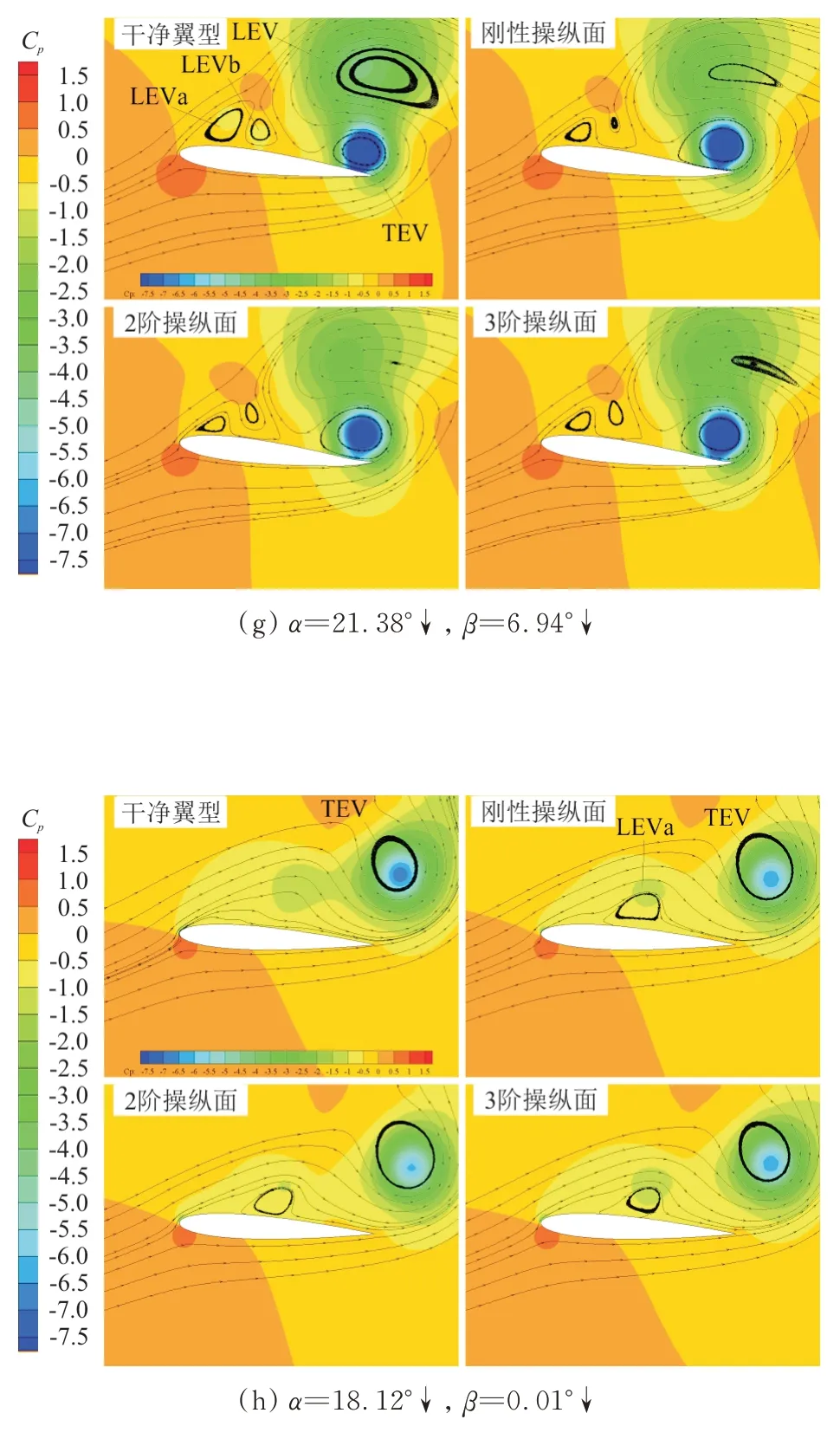
圖8 典型時刻的壓力系數(shù)云圖和流場圖Fig.8 Typical instantaneous Cp counter and streamlines
當(dāng)攻角增大超過靜態(tài)失速攻角(16.00°)之后,翼型上表面的流動仍將保持完全附著。從圖8(a)可以看出:到α
=24.81°↑時刻,各個翼型的后緣上翼面都出現(xiàn)了大面積的封閉回流區(qū)域,形成了一個穩(wěn)定的后緣附著渦(Attached Trailing-edge Vortex,簡稱ATEV);干凈翼型的上翼面同時還出現(xiàn)了前緣渦(Leading-edge Vortex,簡稱LEV),干凈翼型進(jìn)入動態(tài)失速階段;后緣操縱面向上偏轉(zhuǎn)了12.90°時,三個帶操縱面翼型的上表面只有后緣附著渦。可見,向上偏轉(zhuǎn)后緣操縱面將推遲前緣渦的產(chǎn)生。隨著后緣附著渦的增強,對翼型表面的壓力分布會產(chǎn)生更大的影響,干凈翼型的俯仰力矩系數(shù)也會偏離先前變化緩慢的趨勢而迅速趨向負(fù)的極值,俯仰力矩發(fā)生失速。當(dāng)攻角由24.71°↑增至24.96°↑時,干凈翼型的升力線斜率增大。從圖8(b)可以看出:此時升力的增大是后緣附著渦和前緣渦共同作用的結(jié)果,三個帶后緣操縱面機翼的上翼面也都出現(xiàn)了前緣渦,只是不如干凈翼型上的前緣渦發(fā)展得充分。
圖8(c)是攻角上行到最大值時刻的流場情況,可以看出:和上一時刻相比,前緣渦開始往下游移動。當(dāng)后緣附著渦和前緣渦的區(qū)域持續(xù)增大時,在前緣渦的上游位置出現(xiàn)了一對反向旋轉(zhuǎn)的小渦(LEVa 和LEVb)。由于這對小渦與先前生成的后緣附著渦和前緣渦相比,在尺寸和強度上要小很多,通常被稱為次級渦,文獻(xiàn)[30-31]中也描述了類似的流動現(xiàn)象。
在翼型攻角下行的初始階段,前緣渦繼續(xù)向下游移動且區(qū)域逐漸增大,而后緣附著渦的區(qū)域?qū)⒅饾u縮小,最終被前緣渦合并。在經(jīng)歷一段短暫的振蕩之后,干凈翼型的升力系數(shù)在α
=24.53°↓時達(dá)到第二個峰值點(C
=2.25),隨后急劇下降,升力發(fā)生失速。從圖8(d)可以看出:前緣渦已將后緣附著渦吸收,并移動至弦長中點位置。干凈翼型后緣的下游區(qū)域出現(xiàn)一個小渦,隨后立即消失。三個帶操縱面翼型的流場結(jié)構(gòu)基本相似,上翼面只有前緣渦和一個靠下游的次級渦,先前靠上游的次級渦已被前緣渦合并吸收。從圖8(e)可以看出:干凈翼型上翼面一共有四個渦結(jié)構(gòu),后緣渦(Trailing-edge Vortex,簡稱TEV)已經(jīng)出現(xiàn)。由于前緣渦已經(jīng)開始從翼面分離,后緣上翼面已有足夠的空間,使得下翼面的氣流能以平滑的方式調(diào)頭回流到達(dá)上翼面。后緣渦最早出現(xiàn)在剛性操縱面上,但此時3 階操縱面上后緣渦核區(qū)域的壓力系數(shù)更低,說明發(fā)展得更為迅速。
干凈翼型的俯仰力矩系數(shù)在攻角下行至α
=21.91°時達(dá)到負(fù)的極值。從圖8(f)可以看出:前緣渦已經(jīng)從干凈翼型上翼面完全脫離,此時位于后緣渦的正上方。這兩個渦核的低壓區(qū)域?qū)⒄麄€翼型的壓心移到了靠近后緣的位置,由此產(chǎn)生一個極大的低頭力矩。后緣操縱面偏轉(zhuǎn)后,翼型的俯仰力矩系數(shù)已在稍早的時刻達(dá)到負(fù)的極值點,此時前緣渦的分離發(fā)展得更為充分。從圖 8(a)~圖 8(f)可以看出:在翼型的動態(tài)失速過程中,前緣渦在發(fā)展和分離的過程中會直接與其上下游的其他渦發(fā)生相互作用。從圖8(g)可以看出:前緣渦已越過干凈翼型的后緣點,并向尾流中移動;在三個帶操縱面翼型的流場中,前緣渦的環(huán)形流動區(qū)域變得十分扁平,表明操縱面的偏轉(zhuǎn)加速了前緣渦的發(fā)展,尤其在2 階操縱面的流場中,前緣渦已幾近消失。
從圖8(h)可以看出:隨著攻角繼續(xù)下行減小,干凈翼型上的次級渦會演化消失,后緣渦從后緣上翼面脫落并進(jìn)入尾流中;在三個帶操縱面翼型的流場中,次級渦繼續(xù)向下游移動并最終從翼面分離,而后緣渦在尾流中發(fā)展得更加迅速。
由于流場的滯后效應(yīng),直到α
=9.86°↓時,操縱面偏轉(zhuǎn)對流場的影響才完全消失,即四個翼型的流場形態(tài)基本相同。此時,從翼型前緣開始,上翼面的氣流在約50%弦長的范圍內(nèi)恢復(fù)了附著。綜上,在翼型發(fā)生動態(tài)失速時,向上偏轉(zhuǎn)后緣操縱面可以推遲前緣渦的生成,加速前緣渦的發(fā)展;對后緣渦而言,能加快其生成,而對其演化消失影響不大。
后緣操縱面減緩動態(tài)失速的機理可以通過翼型表面的壓力分布進(jìn)一步揭示,如圖9 所示。
從圖 9(a)可以看出:在圖 8(e)時刻,后緣渦在三個帶操縱面翼型上發(fā)展得更為充分,因此干凈翼型的壓力系數(shù)曲線峰值是最低的。從圖9(b)可以看出:在圖8(f)時刻,后緣操縱面偏轉(zhuǎn)顯著降低了翼型后緣的壓力分布峰值,進(jìn)而減小了翼型的低頭力矩。其中,2 階操縱面對應(yīng)的峰值最低,因此減緩效果最好。

圖9 翼型表面壓力系數(shù)曲線Fig.9 Pressure distribution on different airfoils
5 結(jié) 論
(1)當(dāng)采用相同的正弦脈沖偏轉(zhuǎn)信號時,連續(xù)變彎度操縱面能使翼型后緣的壓力分布下降更多,因此對動態(tài)失速的減緩效果優(yōu)于剛性操縱面。
(2)在減小俯仰力矩負(fù)的極值和減小一個運動周期的負(fù)氣動阻尼方面,2 階后緣操縱面的動態(tài)失速減緩效果最好。
(3)相比于剛性操縱面和3 階后緣操縱面,2階后緣操縱面在一個偏轉(zhuǎn)周期內(nèi)的鉸鏈力矩系數(shù)極值最小,因此需要的驅(qū)動能量輸入也最小。

