水下并聯超空泡射彈外彈道數值分析

韓玉晶,李 強,王 辰,蔡 濤

(1.中北大學 機電工程學院,山西 太原 030051;2.重慶長安望江工業集團有限公司,重慶 401120)

超空泡原理在現代武器水下發射中得到了廣泛應用,國內外研究學者針對單發超空泡射彈開展了大量研究。在國外,CAMERON等[1]進行垂直射彈入水實驗,對超空泡的演化、彈道變化等做了詳細觀察和分析;NEAVES等[2]應用時間導數預處理方法對彈丸入水可壓縮多相流進行了模擬;ABRAHAM等[3]使用數學模型研究了彈丸入水運動后的受力變化。在國內,文獻[4]對高速超空泡射彈入水流場與彈道特性開展了數值計算;施紅輝等[5-7]、魏英杰等[8-9]進行了大量超空泡射彈高速入水實驗與數值模擬研究;李強等[10-11]通過數值模擬的方法分析了空化器,轉速、初速度和入水角等不同因素對彈道特性和入水特性的影響。

近年來,也有一些學者開展了多發超空泡射彈的研究。JIANG等[12]對超聲速彈丸的并聯入水過程進行了數值模擬,但所用彈丸結構較為簡單。何春濤等[13]、路麗睿等[14]研究了入水速度對圓柱體并聯入水的影響,但入水速度較低。可以看出,針對水下并聯發射超空泡射彈的研究較少。因此,本文采用重疊網格技術,對彈丸水下發射開展了數值計算研究,對比分析了并聯發射同步與異步水下發射過程中的流場形態與彈丸受力的異同,相關研究成果可為超空泡射彈的設計提供一定的理論參考。

1 數學方程

1.1 控制方程

文中采用VOF多相流模型處理汽水交界面。根據文獻[15]的研究結果,當水下超空泡射彈的運動速度大于900 m/s時液體可壓縮性才會對計算結果產生明顯的影響。因此針對本文300 m/s的運動速度,為提高計算收斂性,視水為不可壓縮流體。針對三維不可壓縮流動,本文采用的控制方程如下:

連續性方程:

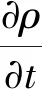
(1)

式中:ρ為混合物密度;t為時間;U為速度。

動量守恒方程:

(2)

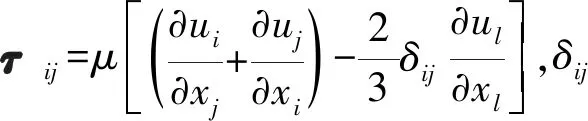
管理可以簡化為PDCA循環。這是一個持續改進模型，他包括持續改進與不斷學習的四個循環反復的步驟，即計劃（Plan）、執行（Do）、檢查（Check/Study）、處理（Act）。 PDCA工具最早起源于貝爾實驗室，是休哈特博士提出的最早使用的管理工具，后來被戴明帶去日本，被豐田普及。到目前為止，我認為PDCA是最有效、總結最到位的管理工具，核心是定目標、定策略，找差距，分析原因，找對策。

1.2 湍流模型

本文采用Standardk-ε模型作為湍流模型,其適用范圍廣,計算收斂性好,方程式如下:

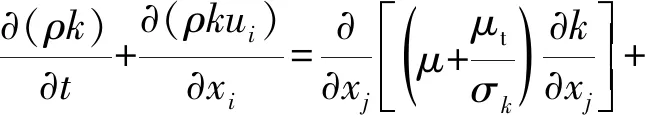
(3)

(4)

式中:k和σk分別為湍流動能和耗散率;μt為湍流黏性系數;σk=1,σε=1.3;Gk為速度梯度湍流動能;Gb為浮力湍流動能;YM為可壓湍流中振蕩膨脹對耗散率的貢獻;Sk,Sε為附加源項;C1ε,C2ε,C3ε為常數。

1.3 空化模型

本文采用Schnerr-Sauer空化模型用于數值計算,該模型將蒸汽相的體積占比與液體中的空泡數聯系起來,通過求解液體中的空泡數來計算蒸汽相的體積占比,這種方法簡化了計算過程,且使用限制少,計算準確度高,因此在實際計算中得到了廣泛應用,其方程式為

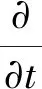
(5)

(6)

(7)

式中:αv為氣相體積分數,ρv為氣相密度,ρl為水的密度,Re為蒸發速率,Rc為冷凝速率,vv為水蒸氣相的速度矢量,rB為氣核的半徑,pv為水的飽和蒸汽壓。

2 計算模型設置

2.1 幾何模型

本文參考挪威DCG超空泡射彈建立幾何模型。該彈丸直徑D=12.7 mm,彈長95 mm,彈質量58 g,頭部設有空化槽,彈丸初速300 m/s。圖1為該彈丸的模型示意圖,為便于討論,如圖所示定義了彈丸內側和外側。同時,定義彈丸的間距為Δd,發射時間間隔為Δt。對于同步發射工況,Δt=0,Δd分別設置為2D、3D、4D。對于異步發射工況,彈丸間距固定為2D,兩彈丸的發射時間間隔Δt分別設置為0.05 ms、0.1 ms、0.2 ms和0.35 ms。

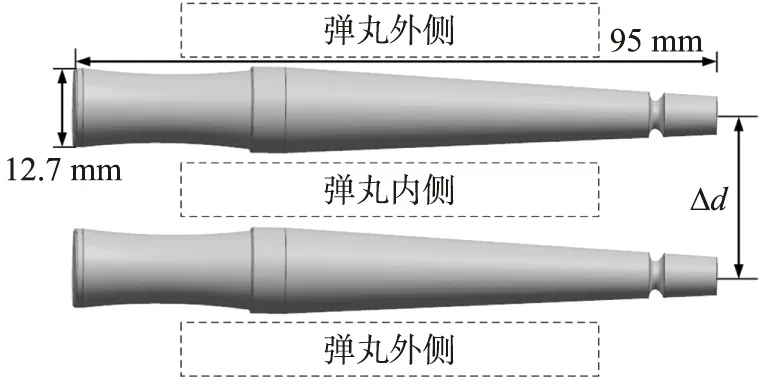
圖1 幾何模型

2.2 網格劃分與計算域設置

網格劃分對計算結果有著很大的影響,本文采用了重疊網格技術,其在網格運動過程中不涉及網格重構,因此可以減少計算誤差。圖2為網格劃分示意圖。計算域可以分為三大部分:彈丸重疊域、加密背景域、外部背景域。其中彈丸重疊域網格最密,以精確捕捉彈丸附近的流場形態,加密背景域網格也較密,減少與重疊域進行數據交換時的誤差,外部背景域網格較疏,加快收斂速度。圖3為整體計算域示意圖,為節約計算成本,使用1/2彈丸進行計算,并開啟三自由度模型控制彈丸的運動。

圖2 網格劃分示意圖

圖3 整體計算域示意圖

2.3 邊界條件及算法設置

為順利完成水下并聯超空泡射彈的數值模擬,需要對邊界條件進行正確設置。本文對計算域外邊界設置壓力出口邊界條件,彈丸表面設置為壁面;彈丸重疊域與加密背景域采用overset邊界條件進行數據交換,加密背景域和外部背景域采用interface邊界條件進行數據交換。此外,采用PISO算法處理速度與壓力耦合。計算步長為5×10-6s,計算步數為1 000步。

2.4 數值方法驗證

本文根據文獻[16]中的實驗數據,對水下并聯發射超空泡射彈的數值模擬方法進行驗證。計算模型如圖4所示,射彈長度L2為240 mm,直徑D1為19 mm,質量為0.179 kg,兩射彈間距為2D1,射彈初速為81.2 m/s。實驗值與計算值對比結果如圖5所示。從圖5(a)可以看出,數值計算結果的空泡形態與實驗值較為吻合,從圖5(b)可以看出,速度誤差值最大為1.58%,從而驗證了本文所采用的數值方法對水下并聯發射問題具有較好的適用性。

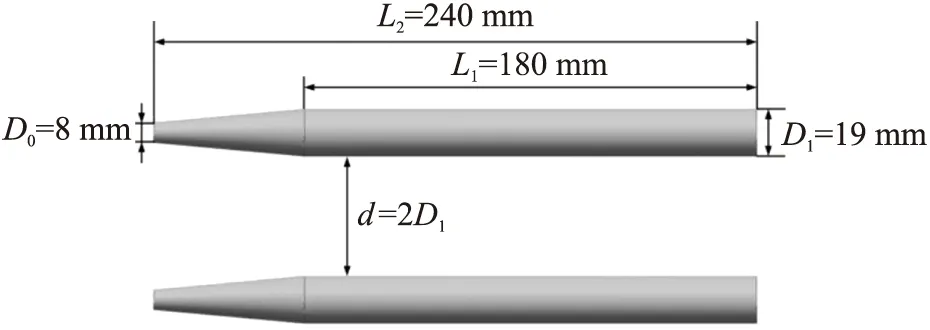
圖4 水下并聯發射射彈

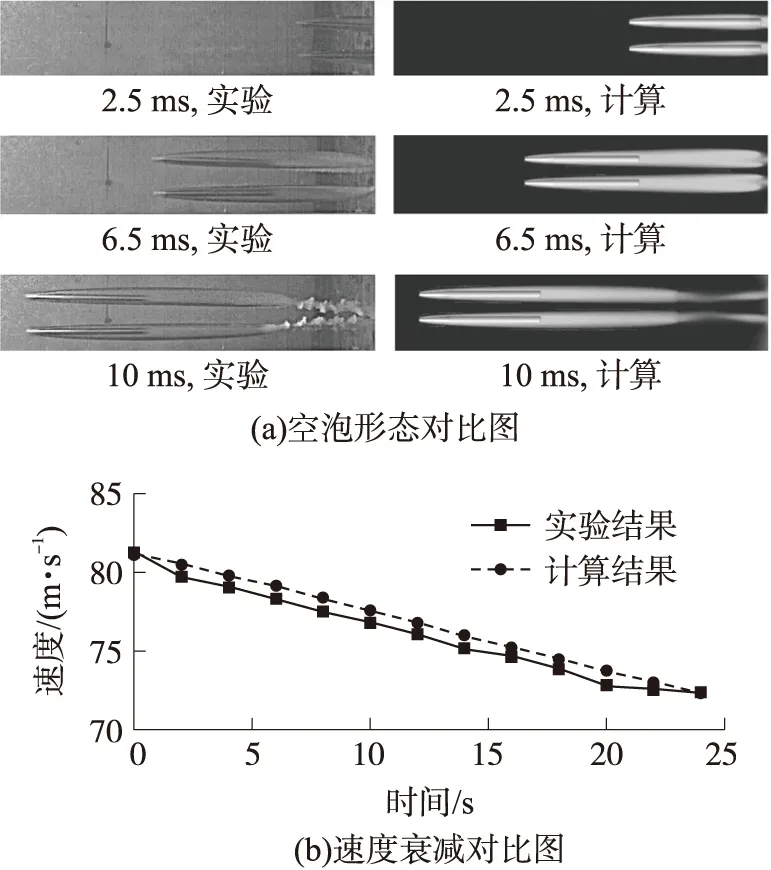
圖5 水下并聯發射數值驗證結果

2.5 網格無關性驗證

網格無關性驗證在于選取合適的網格數量,滿足計算精度的同時,提高計算速度。對前文DCG超空泡射彈模型的網格進行無關性驗證,網格數量分別為60萬、80萬和100萬。選擇彈丸軸向速度衰減情況作為判據,計算結果如圖6所示。從圖6可以看出100萬與80萬網格彈丸速度變化規律幾乎一致,60萬網格速度衰減略快,綜合考慮計算結果,現選擇網格數為80萬的網格進行計算。

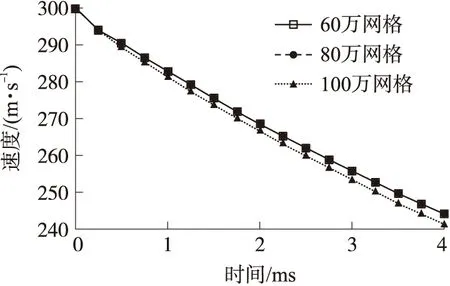
圖6 彈丸軸向速度衰減曲線

3 計算結果分析

本文分別對水下同步發射與異步發射超空泡射彈開展了數值模擬研究,計算工況如表1所示。

表1 計算工況表

3.1 水下同步并聯發射超空泡射彈數值模擬

圖7為水下同步發射超空泡射彈運動0.1 ms時的空化云圖,圖8為水下同步發射超空泡射彈運動1.5 ms時的空化云圖。從圖7可以看出,在彈丸初始運動階段,空泡首先在頭部和尾部產生,并聯工況的內側空泡尺寸小于外側空泡尺寸,且間距越小,內外側空泡尺寸相差越大。在彈丸運動一段時間后,從圖8可以看出,單發超空泡射彈的空泡對稱性較好,彈丸被完整包裹在空泡內,空泡尾部也呈現出對稱的葫蘆狀外形,因此彈丸受到的水動力較為平衡,能夠在運動1.5 ms后保持彈道的穩定性。而對于Δd=2D和Δd=3D的工況,彈丸均出現了不同程度的偏轉,且彈丸間距越小,偏轉程度越明顯。這是由于在并聯工況下,兩彈丸中間由于水的排擠作用,內側的空泡發展擴張受到抑制,而外側的空泡自由擴張,總空泡尺寸減小,尾部的空泡也不再是葫蘆狀,使彈丸受到了不對稱的水動力作用,引起了彈丸的偏轉。對于Δd=4D的工況,可以發現由于彈丸相隔較遠,兩彈丸的空泡獨立發展,空泡尾部也沒有像彈丸相隔較近時一樣融為一體,因此空泡形態和尺寸均與單發相似,彈道也較為穩定。

圖7 水下同步發射0.1 ms時超空泡射彈空化云圖

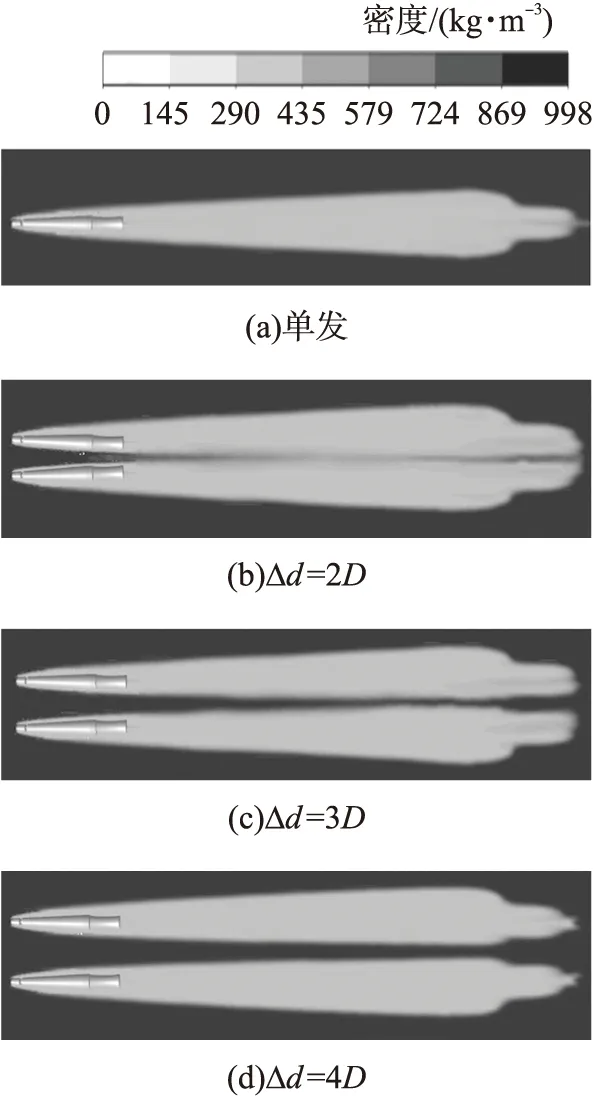
圖8 水下同步發射1.5 ms時超空泡射彈空化云圖

圖9為彈丸質心位置的橫向偏移量(沿X軸)隨時間變化圖。可以看出,單發與Δd=4D工況的彈丸彈道軌跡穩定,運動時間4 ms時和運動距離約為1 m時的偏移量分別為0.086 mm和0.103 mm,彈丸沒有發生明顯的偏轉。在Δd=2D的工況下,彈丸在運動2.5 ms時偏移量突然開始激增,而Δd=3D的工況下,彈丸運動3 ms時偏移量開始減小。為解釋二者偏移軌跡趨勢不同的原因,圖10給出了不同間距下的彈丸側向力變化曲線。在初始運動階段,正如圖9分析,彈丸受到不對稱的水動力作用發生了偏轉。對于Δd=3D的工況,相對偏轉角速度較小,當彈丸尾部觸碰到空泡邊界時,由于空泡內外的壓差,彈丸尾部將產生回轉力矩,該回轉力矩足以抵消引起彈丸失穩的偏轉力矩,如圖10所示彈丸受到的側向力方向突變為負,使得彈丸彈回空泡內部,即發生了尾拍現象,因此運動1 m后彈丸偏移量小于1 mm。但是Δd=2D的工況下彈丸相隔較近,偏轉力矩遠大于回轉力矩,因此在到達空泡邊界后側向力仍然很大,彈丸繼續向X正向偏轉,彈丸大面積暴露在水中,無法維持彈道穩定,在運動4 ms后的偏移量為4.45 mm,遠大于其他工況。綜上,對于同步并聯工況,彈丸觸碰空泡邊緣的時刻為運動偏移趨勢發生改變的時刻,彈丸間距較小時彈丸產生失穩現象,而彈丸間距較大時,彈丸將發生尾拍現象,維持運動穩定性。

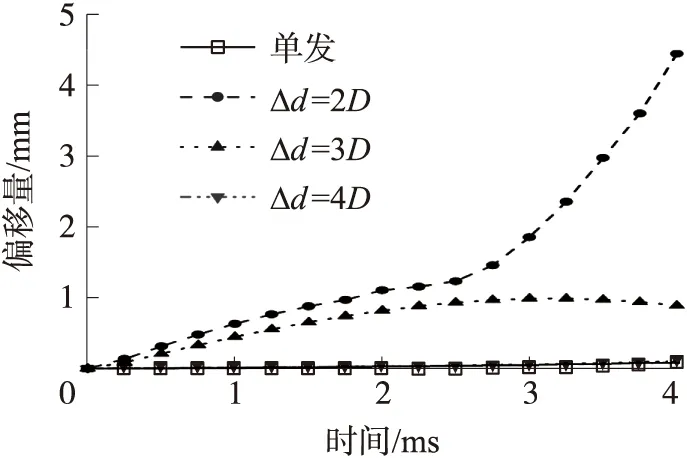
圖9 水下同步發射彈丸運動偏移量曲線

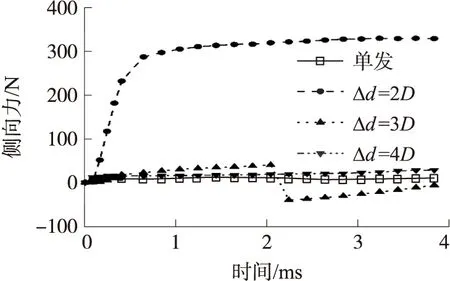
圖10 水下同步發射彈丸側向力變化曲線

圖11為不同工況下彈丸速度衰減曲線,圖12為彈丸阻力隨時間變化曲線。可以看出,不同工況下的彈丸速度衰減和阻力變化較為相似,開始運動時空泡尚未形成,阻力較大,速度衰減較快,隨后在彈丸周圍形成了超空泡,減小了水下運動時的阻力,速度衰減變慢。但放大曲線后發現速度和阻力變化仍有區別,彈丸間距越小,速度值下降越大,這主要是因為彈丸間距較小時,彈丸內側的空泡發展受到抑制,不能完全包裹彈丸,彈丸表面出現了沾濕現象,彈丸所受的黏性阻力增大,引起了速度衰減變快。因此,并聯入水不僅會引起彈道穩定性下降,同時也會對超空泡射彈的減阻性能產生不利影響。

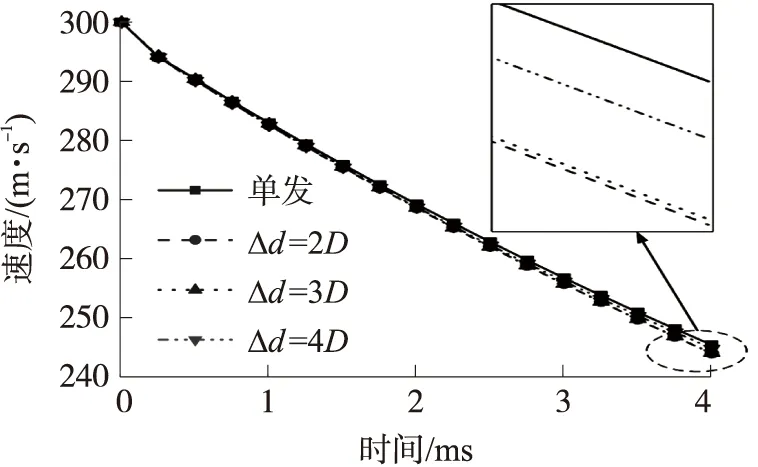
圖11 彈丸速度衰減曲線

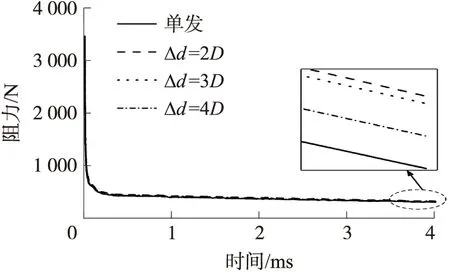
圖12 彈丸阻力變化曲線

3.2 水下異步并聯發射超空泡射彈數值模擬

同步發射只是并聯發射的一個特殊情況,但在實際作戰的大部分情況中,兩彈丸發射將有時間間隔,因此對異步發射工況進行研究有著重要的現實意義。圖13為發射時間間隔分別為0.05 ms、0.1 ms、0.2 ms、0.35 ms時的水下超空泡射彈空化云圖。可以看出,與同步發射不同的是,在異步發射下兩發彈丸的空泡不再有相同的形態。當發射時間間隔較短時,兩彈丸之間的干擾依然很強,彈丸內側的空泡小于外側,這一規律與同步發射類似,隨著時間間隔的變大,先發彈丸受后發彈丸的影響逐漸變小,附近的空泡對稱性逐漸變好。但是后發彈丸外側擴張程度明顯大于內側空泡,當時間間隔大于0.2 ms時的后發彈丸的內側空泡將先發彈丸后方的空泡完全夾斷,通過分析壓力場可以對這一現象進行解釋。圖14為水下異步發射壓力云圖。

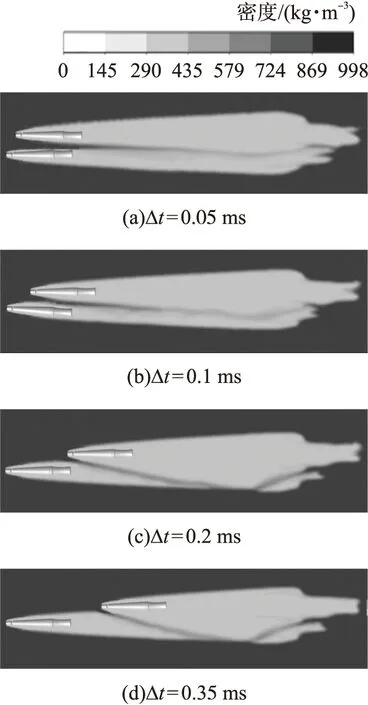
圖13 水下異步發射超空泡射彈空化云圖

圖14 水下異步發射壓力云圖

由圖14可以看出,對于水下超空泡射彈而言,高壓區出現在彈尖位置,其他位置的壓力值相對較低,而彈附近被空泡包裹,空泡內壓力值比周圍的水域更低,為低壓區。隨著時間間隔的增加,后發彈丸的內側更加遠離先發彈丸的高壓區,并靠近先發彈丸的低壓區,低壓對空泡的擴張有促進作用,因此后發彈丸的內側空泡擴張程度遠大于外側。分析彈前高壓區,可以看出先發彈丸彈前壓力幾乎不受后發彈丸影響,4種工況下的壓力最大值基本相同,且彈前壓力沿彈丸軸線呈對稱分布;對于后發彈丸,可以看出Δt=0.05 ms和Δt=0.1 ms工況,由于受先發彈丸超空泡影響較小,彈前壓力分布較為對稱;而對于Δt=0.2 ms和Δt=0.35 ms工況,彈丸內側更靠近先發彈丸生成空泡的氣體域,彈丸外側靠近水域,氣體域密度遠小于水域,因此彈前高壓區不再呈對稱分布,內側壓力低而外側壓力高。同時,隨著時間間隔的增大,先發彈丸空泡發展更加完整,因此后發彈丸內側壓力減小幅度更大。

圖15為異步發射彈丸的速度衰減曲線。可以看出,先發彈丸的速度衰減差別相對較小,運動4 ms之后各工況下的速度衰減差別在0.5 m/s之內,說明后發彈丸對先發彈丸的速度影響較弱。但是后發彈丸的速度衰減出現了一定的差別,時間間隔越大,后發彈丸的速度衰減越慢,運動4 ms時,Δt=0.35 ms工況下的存速與Δt=0相比大了約5 m/s。根據圖13和圖14分析其原因,雖然后發彈丸內外側空泡的發展都沒有受到抑制,空泡對彈丸的包裹性良好,彈丸沒有出現沾濕現象,但后發彈丸在先發彈丸所生成的空泡中運動,從而導致了后發彈丸所受阻力減小,速度衰減變慢。

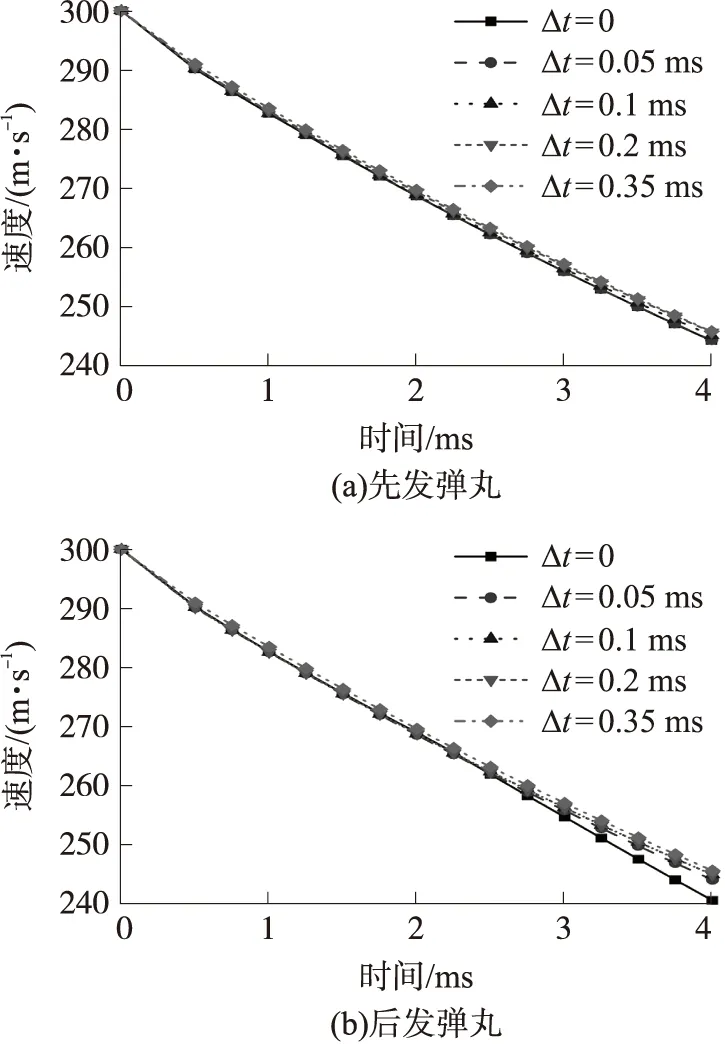
圖15 水下異步發射彈丸速度衰減曲線

圖16為水下異步發射彈丸運動偏移量曲線。由圖可知,先后發射的兩發彈丸同樣有著不同的規律。從圖16(a)可以看出,對于先發彈丸,與同步發射相比,Δt=0.05 ms工況下彈丸偏移量明顯增加,而Δt=0.1 ms時彈丸偏移量稍微減小,并且彈丸發生尾拍現象。對于Δt=0.2 ms和Δt=0.35 ms工況,彈丸運動軌跡相對穩定。因此隨著時間間隔的增加,先發彈丸的偏移量先增加后減少。該現象產生的原因為:隨著時間間隔的增加,后發彈丸對先發彈丸的干擾力作用點逐漸靠后。在Δt=0.5 ms工況時,兩發彈丸之間的干擾與同步發射相比區別較小,而干擾力的合力更靠近彈丸尾部,彈丸更加容易發生偏轉。當時間間隔進一步增加時,后發彈丸對先發彈丸的干擾力迅速衰減,因此先發彈丸的偏移量逐漸減小。

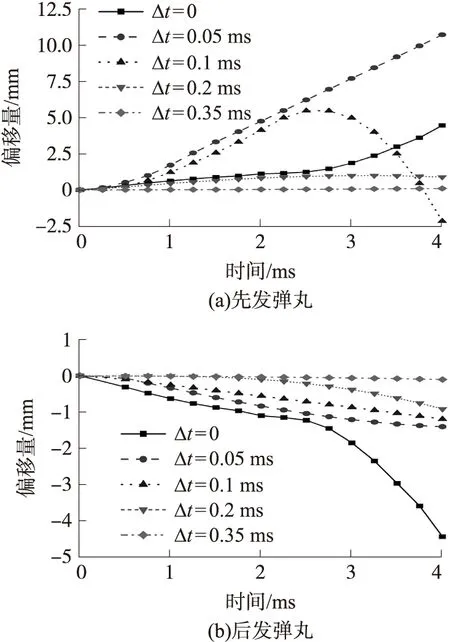
圖16 水下異步發射彈丸運動偏移量曲線

從圖16(b)可以看出,對于后發彈丸,時間間隔的越大,其彈道偏移量越來越小,這一現象與先發彈丸并不相同。通過圖10分析其原因,在時間間隔較小時,后發彈丸內側空泡的發展受第一發彈丸的影響擴張受到抑制,彈丸內側沾濕,橫向力方向指向彈丸外側,造成彈丸偏轉,隨著時間間隔的增加,內側空泡發展的抑制解除,并逐漸開始過度擴張。此時彈丸內外側都沒有沾濕現象,彈丸受力較為均勻,因此彈道穩定性較好。

4 結論

本文對不同工況下的水下并聯超空泡射彈開展了數值模擬研究,得出的主要結論如下:

①對于同步發射彈丸,內側空泡發展受到抑制,彈丸內側出現明顯的沾濕現象,彈丸在不對稱的水動力作用下向外側偏轉。彈丸間距越小,彈道穩定性越差。當彈丸間距增加至4D以上時,兩彈丸之間的干擾可忽略不計。

②對于異步發射先發彈丸,隨著發射時間間隔的增加,速度衰減規律基本不變,但其彈道偏移量先增大后減小。

③對于異步發射后發彈丸,隨著發射時間間隔的增加,內側空泡擴張的抑制作用逐漸解除,并有過度膨脹的趨勢。此外,隨著時間間隔的增加,速度衰減的幅度減小,彈道偏移量也逐漸減小。